基于改进SPSO-BP神经网络的温度传感器湿度补偿*

2018-04-11行鸿彦张一波

传感技术学报 2018年3期

行鸿彦,郭敏,张兰,张一波

(1.南京信息工程大学气象灾害预报预警与评估协同创新中心,南京 210044;2.南京信息工程大学江苏省气象探测与信息处理重点实验室,南京 210044)

近年来,HMP45D温湿度传感器被广泛应用在自动气象站中,它是用铂电阻传感器Pt100来测量温度的。铂电阻材料有很多优点[1-2],如:测温精确度高,性能好,操作简单,适用范围广等。但是,在实际应用中,湿度,辐射等诸多因素影响着温度传感器的测量结果[3-4],使其呈现一种非线性的趋势,严重影响了温度传感器测量的精确度。和其他因素相比,湿度对温度传感器的测量结果影响最大,所以,对温度传感器进行湿度补偿是十分必要的,来增强测量精确性,减小误差。

为了尽量提高温度传感器测量的精确度,减小因湿度带来的误差,可以从硬件电路和软件两方面进行补偿。硬件电路[5-6]补偿方法的电路繁琐,操作困难,不易理解,并且电路中的一些元件受到湿度变化还会产生温度漂移的现象,使得温度传感器测量结果的准确性变低。软件补偿方法有模拟退火方法、差分进化算法、禁忌搜索、BP神经网络等[7-10]。模拟退火算法质量高,初值鲁棒性强,简单易懂,但它的初始温度要高、终止温度要低、降温速率要慢,抽样数量要多,因此优化过程较长。差分进化算法的原理简单,受控参数少,但随着迭代次数的增加,个体间的差异会逐渐减小,影响变异的多样性。禁忌搜索算法的记忆力强,可以接受不好的值,具有很强的“爬山”功能,但过分依赖初始解。虽然在文献[10]中BP神经网络对铂电阻温度传感器产生的误差有了一定的补偿效果,但它的收敛速度仍旧非常缓慢,进入局部极小的情况仍旧很多。

本文在现有研究的基础上,利用改进的简化粒子群算法优化BP神经网络的模型对温度传感器进行湿度补偿。通过对基本粒子群的分析,找到不受速度影响的简化粒子群算法,同时对其惯性权重采用线性递减的方法。利用改进的简化粒子群算法的迭代找到最优位置,即最优权阈值,将该值赋给BP神经网络并训练网络,补偿湿度给温度传感器测量带来的影响。与BP神经网络对比,进一步表明改进SPSO-BP算法在温度传感器湿度补偿上的优越性。

1 算法介绍

1.1 基本粒子群算法(PSO)

粒子群优化算法[11-13]最早起源对鸟群飞行情况的研究,是一种群体智能算法。在SPO算法中,每个“粒子”都代表优化问题的一个可能解。粒子群算法开始初始化产生一群随机粒子,利用迭代得到最优位置。在D维搜索空间内,随机初始形成一个由n个粒子组成的种群,其中每个粒子的当前位置可表示为Xid=(Xi1,Xi2,…,XiD),速度为Vid=(Vi1,Vi2,…,ViD),个体极值为Pid=(Pi1,Pi2,…,PiD),全局极值为Pg=(Pg1,Pg2,…,PgD)。在每次迭代中,根据如下公式更新粒子的速度和位置。

(1)

(2)

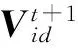
1.2 简单粒子群算法(SPSO)

PSO算法[14-15]包含了速度和位置两个向量,在每次迭代中都需要更新两个向量,算法比较复杂,同时在迭代的后半段收敛速度缓慢,极大可能得进入局部极值,影响算法精度。因此,很多学者对此进行了改进,文献[14]证明了粒子群进化过程是和速度没关系的,其大小只代表粒子向最优解移动的快慢,是可以去掉的。每次迭代仅由位置这一向量控制,提出了简化粒子群优化算,将原来的二阶方程降为一阶,并证明了其收敛性。去掉速度向量后的简化粒子群算法的方程表示为:

(3)

1.3 改进的SPSO

惯性权重w[16-17]是个重要的参数,主要用于维持算法局部搜索能力和全局搜索能力之间的平衡性。在简化粒子群算法中,w一般为固定值,这就说明在算法迭代过程中,w值是不变的。而通过大量实践发现,固定值的效果是不理想的。在优化初期,w应该取为较大值,增强全局寻优能力,这样有利于跳出局部极小,而随着优化过程的不断推进,w应逐渐减小,这样有利于增强局部搜索能力,提高算法的收敛速度。在此基础上,本文采用线性递减的方法改变权重,使得权重值从开始的最大值逐渐减小到最小值,增强局部寻优能力,即:

(4)

wmax为定义的最大惯性权重,wmin为定义的最小惯性权重,t为当前迭代次数,tmax为最大迭代次数。

2 基于改进SPSO-BP神经网络的湿度补偿算法

将改进的SPSO与BP神经网络相结合[18-20],就是利用改进的SPSO算法的全局优化能力解决BP神经网络容易陷入局部极小的问题。定义改进的SPSO中粒子的每个维度分量与BP神经网络中的权阈值相对应,通过迭代得到粒子的最优位置从而得到BP神经网络的最优权阈值,将该值赋给BP神经网络做为新的网络连接权值和阈值,训练BP神经网络。我们定义改进简化粒子群算法的适应度函数为BP神经网络输出值与期望值的误差的均方值,表示为:

(5)

具体步骤如下:

①初始化神经网络结构,根据所需求解问题设定BP神经网络输入层个数为l、输出层个数为n,计算出隐含层个数J,同时设置训练样本数m,测试样本数t、网络目标误差ε等参数。

②设定简化粒子群算法的维数D和规模N,随机初始化每个粒子的位置,将其限制在所规定的范围内,同时设置算法的最大迭代次数itmax,学习因子c1、c2,惯性权重wmax、wmin等参数。

③通过适应度函数,计算每个粒子的适度值F,将第i个粒子的位置设为个体极值Pid,比较所有粒子个体极值的适应度值,适应度值F最小的粒子的位置设为种群全局极值Pg。

④根据式(3)～式(5)更新粒子i的位置,若超过所设定的范围,取边界值,计算粒子i的适应度值F。

⑤如果粒子i的适应度值F(Xi)小于粒子个体极值Pid的适应度值F(Pid),则用粒子此时的位置Xi替换Pid,如果F(Xi)小于种群全局极值Pg的适应度值F(Pg),则用粒子此时的位置Xi替换Pg。

图1 改进SPSO-BP 流程图

⑥若迭代次数达到预设的最大迭代次数itmax,终止迭代,输出粒子的全局最优解Pg,也就BP神经网络的最优权阈值,如没有达到,返回步骤④继续迭代搜索。

改进SPSO-BP神经网络的流程图如图1所示。

3 HMP45D温度传感器检定结果分析

3.1 影响因素理论分析

HMP45D温湿度传感器是利用铂电阻在温度变化时自身电阻值随之改变的特性来测量温度的,显示仪表将指出铂电阻值所对应的温度值。HMP45D温度传感器电阻和温度之间的关系可用二次多项式函数表表示:

Rt=R0(1+αt+βt2)

(6)

式中:Rt为铂电阻在温度为t℃时的电阻率,R0为铂电阻在温度为0 ℃时的电阻率,为100 Ω,α,β为系数,可以通过对传感器的标定求出其值。通过数据采集器将测得的电阻值的变化转化为电压值的变化,实现对温度的测量。

一般在没有温度变化时,电阻值R是由电阻长度L和电阻的横截面积S决定的,表示为

R=ρL/S

ρ是电阻的电阻率,由其自身性质决定。而当环境湿度变大时,空气中的水分子跟着变多,而电介质的表面会吸附这些水分子,形成一层很薄的膜,影响电阻的电阻率,继而影响了电阻值,也就影响了温度传感器的测量情况,使得温度传感器的测量产生了一定误差,测量精度变低。

3.2 湿度检定结果分析

本文所用的实验数据是2012年课题组在中国气象局气象探测中心实验得到的。在调温调湿的检定箱中进行湿度对温度传感器的影响实验,温度最低可调到-70 ℃,最高到60 ℃,湿度最小可调为0%RH,最大为100%RH,信号为JJQ1型的模拟器作为采集实验所测数据的装置,HMP45D温度传感器作为实验的测量对象。

事先定好实验需要测量的温度点,调好检定箱里的湿度,等到湿度稳定后,按照定好的温度点调整检定箱里的温度,待温度后,读取此时的温度值做为一次数据,实验共读取10次数据,我们将这10次测得温度值的平均值设为温度点的测量值,铂电阻10次输出值的平均值加上修正值作为测量的标准值。依次对设定好的每个温度点进行检定,实验方法和之前一样,直到检定完所有的温度点,实验结束。

所测得的部分数据如表1所示。

根据实验所得数据,用标注值减去测量值得到在不同湿度下实验所得的测量误差值,用这些误差值和湿度值绘成曲线,分析湿度对温度传感器测量带来的影响程度。不同湿度情况下温度传感器的测量误差曲线如图2所示。

表1 湿度对HMP45D型温度传感器的影响部分样本组队

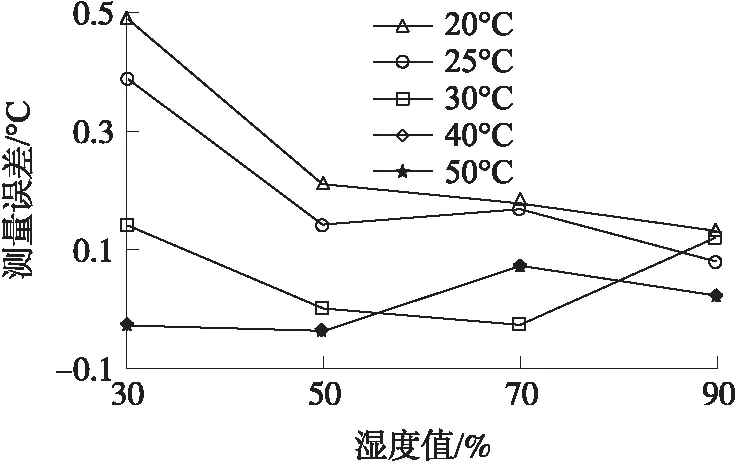
图2 湿度对HMP45D型温度传感器的影响

从图2可以看出,在同一湿度值下,温度值不同,误差是不同的,同时在相同温度值下,湿度值不同,误差也是不一样的,由此可得出湿度对温度传感器的测量带来了巨大了影响,使得测量结果呈现出一种非线性的特征。为了尽量减小湿度变化给温度

传感器测量带来的误差,本文采用改进的SPSO-BP神经网络的方法对其进行补偿。

4 仿真实验

4.1 温度传感器湿度补偿的实现

通过改进SPSO算法优化BP神经网络,按照图2 的步骤对HMP45D型温度传感器进行湿度补偿。将所测数据分为两份,一份作为训练样本,另一份作为测试样本,输入值选湿度影响值和温度测量值,温度测量的标准值作为期望输出值。分别训练改进的SPSO-BP神经网络模型和BP神经网络模型,并对训练结果进行测试,得到的温度传感器湿度补偿后的部分数据如表2所示。

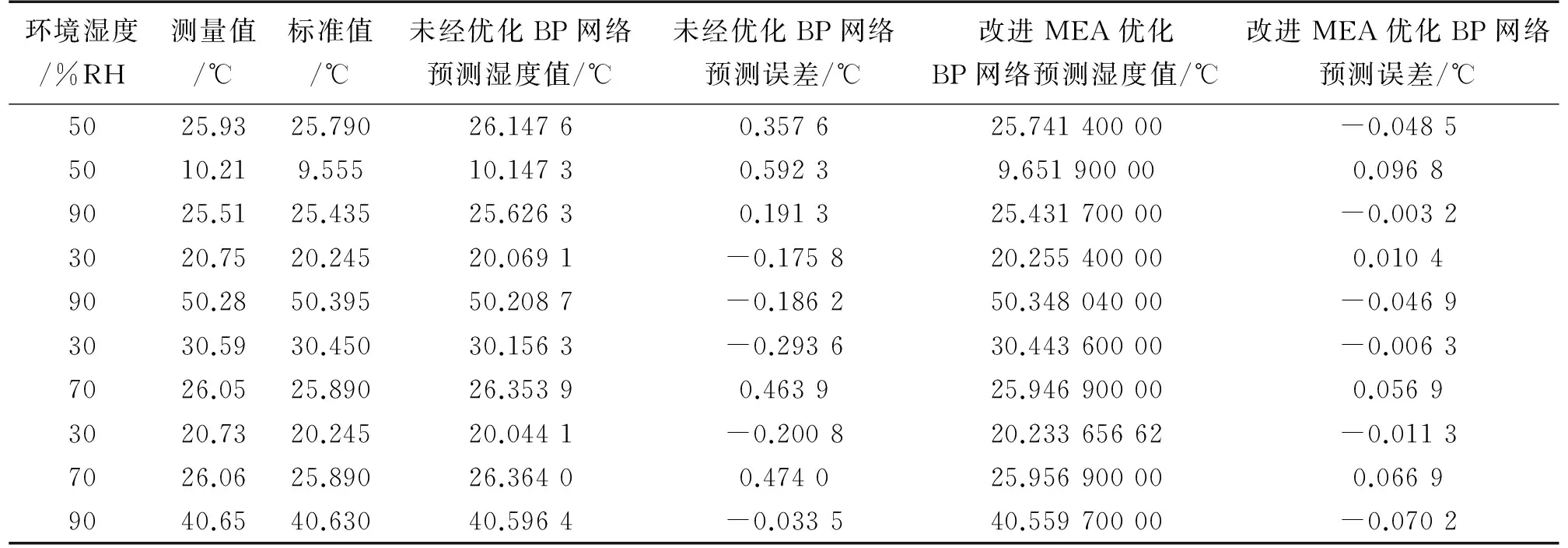
表2 改进简化粒子群算法的BP神经网络模型湿度补偿后的结果

从表2中可以看出,与BP神经网络补偿后的结果相比,改进SPSO-BP神经网络补偿的结果更加接近标准值,其温度误差也明显减小,预测误差最高减小了0.5 ℃,说明改进后的SPSO-BP神经网络更好的对温度传感器进行了湿度补偿,有效消除了由于湿度变化给温度传感器测量带来的影响。

4.2 仿真结果分析

分别对改进的SPSO-BP神经网络方法和BP神经网络方法进行仿真实验,对两者仿真结果进行对比分析。采用三层前向神经网络结构,确定输入节点2个,隐含层节点5个,输出节点1个,学习速率0.1,最大迭代次数为100,目标误差0.000 01,动量因子0.9。根据简化粒子群算法原理,设最大迭代次数为50,最大位置为1,最小位置为-1,学子因子c1、c2为1.491,最大权重值为0.9,最小权重为0.3。

通过改进的简化粒子群算法不断迭代找到粒子的最优位置,也就是BP神经网络的最优权阈值,将得到的最优权阈值赋给BP神经网络作为新的权阈值,用新的权阈值训练BP神经网络,并对训练好的网络进行测试,得到结果如图3和图4所示。

图3中蓝色星号表示实际的期望输出,绿色圆点代表改进SPSO-BP神经网络的预测输出。从图中我们可以看出,绿色圆点和蓝色星号几乎完全重合在一起,充分表明了改进SPSO-BP神经网络模型可以较为准确地预测出系统的输出值。

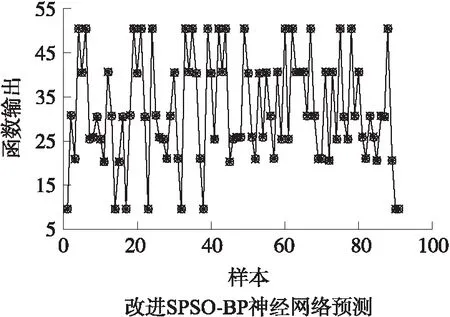
图3 改进SPSO-BP神经网络模型预测输出

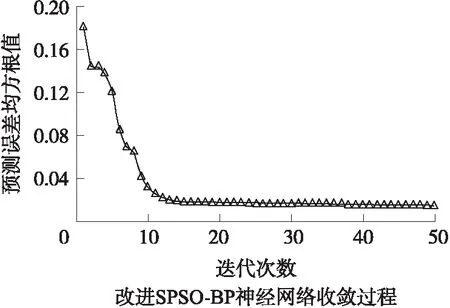
图4 改进SPSO-BP神经网络误差平方和曲线

从图4可以清晰地看出,在迭代次数进行到15代时,预测误差均方根值达到了最小,此时改进SPSO-BP算法已经找到了粒子的最优位置,也就是找到了BP神经网络的最优权阈值,说明改进SPSO-BP算法的收敛速度较快。

4.3 性能分析

根据表2的数据,对改进的SPSO-BP神经网络与传统BP神经网络进行湿度补偿的误差进行对比分析,如图5和表3所示。

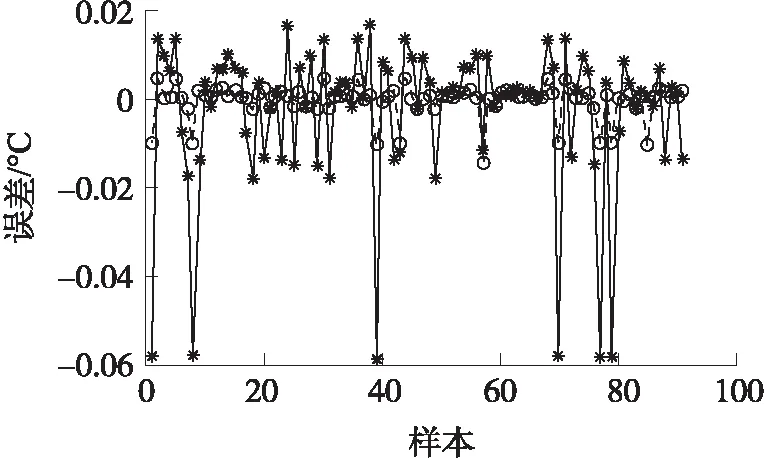
图5 误差曲线

算法同等目标误差下训练次数误差均方值/℃误差绝对值之和/℃传统BP神经网络1200.277621.0695改进的SPSO-BP150.08424.2532

图5中蓝色带星号的曲线是BP神经网络模型湿度补偿后的误差曲线,红色带圆点的曲线是改进SPSO-BP神经网络模型的误差曲线,从图5中可以看出经过改进简化粒子群算法优化的BP神经网络的误差明显小于BP神经网络的误差,说明通过改进简化粒子群算法优化后的BP神经网络的方法要比BP神经网络的方法要好。

从表3中可知,在同等目标误差下,BP神经网络训练120次才达到最优值,而改进粒子群优化后的BP神经网络只要训练15次就达到最优值。且BP神经网络的误差绝对值之和为21.069 5 ℃,误差均方值为0.277 6 ℃,改进简化粒子群算法优化的BP神经网络的误差绝对值之和为4.253 2 ℃,误差均方值为0.084 2 ℃,误差均方值降低了0.1934 ℃,说明改进SPSO-BP神经网络的运行速率快,迭代次数少,补偿精度高,有效地对温度传感器进行了湿度补偿。

5 结束语

本文针对湿度变化给温度传感器测量带来影响的问题,提出了改进简化粒子群算法的BP神经网络模型对湿度进行补偿。通过对基本粒子群算法的介绍,得到了不受速度项约束的简化粒子群算法,同时对其惯性权重采用线性递减的方法。将改进的简化粒子群算法与BP神经网络相结合,就是利用简化粒子群算法的全局搜索解决BP神经网络容易陷入局部极小的问题。与没有优化的BP神经网络模型相比,改进简化粒子群算法的BP神经网络的误差均方值减小了0.193 4 ℃,预测误差最高减小了0.5 ℃,有效提高了温度传感器湿度补偿的精度,同时改进SPSO-BP神经网络的运行速率快,迭代次数少,结构简单易懂,可以很好的投入到实际使用中。

[1] 孙文良,沈秋宇,等. HMP45D温湿度传感器的检定校准[J]. 气象水文海洋仪器,2009(3):124-126.

[2] 刘锋,董蔷薇. HMP45D温湿度传感器的工作原理及维护[J]. 大众科技,2011(4):13-14.

[3] Patrick Carey W,Sinclair S Yee. Calibration of Nonlinear Solid-State Sensor Array Using Multivariate Regressiontechniques[J]. Sensors and Actuators,1992,9(2):113-122.

[4] 王晓蕾,林捷. 自动气象站温度传感器的辐射误差[J]. 解放军理工大学学报,2006,7(4):405-408.

[5] 周胜海. 传感器非线性的硬件校正方法[J]. 仪表技术与传感器,2002,21(5):1-4.

[6] 俞阿龙,李正. 热敏电阻温度传感器的一种线性化设计[J]. 工业仪表与自动化装置,2003(5):19-20,39.

[7] 王洪峰,朱海. 采用遗传-退火算法的网格依赖任务可信调度[J]. 计算机科学,2015(6):268-275.

[8] 邹水平,行鸿彦,于祥. 一种新的温度传感器湿度补偿方法[J]. 南京信息工程大学学报(自然科学版),2016,8(6):533-539.

[9] 彭基伟. 自动气象站温湿度传感器观测数据分析及修正算法研究[D]. 南京:南京信息工程大学,2013.

[10] 刘天键,王劭伯,朱善安. 基于神经网络的铂电阻温度传感器非线性校正方法[J]. 仪器仪表学报,2002,23(5):518-521.

[11] 黄平. 粒子群算法改进及其在电力系统的应用[D]. 华南理工大学,2012.

[12] 刘建华. 粒子群算法的基本理论及其改进研究[D]. 中南大学,2009.

[13] 魏波,李元香,徐星,等. 基于稳定策略的粒子群优化算法[J]. 计算机科学,2011,(12):221-223.

[14] 胡旺,李志蜀. 一种更简化而高效的粒子群优化算法[J]. 软件学报,2007(4):861-868.

[15] 陈琳玲. 基于简化粒子群算法的测试数据自动生成方法研究[D]. 西南大学,2010.