永磁同步电机控制策略对比仿真研究
2018-04-11杜常清曾红霞武冬梅颜伏伍
杜常清,曾红霞,武冬梅,张 佩,颜伏伍
(武汉理工大学 现代汽车零部件技术湖北省重点实验室,湖北 武汉 430070)
随着永磁材料、电子电力技术以及新型电机控制理论的发展,永磁电机越来越多的被应用在电动汽车驱动系统中,尤其是永磁同步电机 (permanent magnet synchronous motor, PMSM)。由于PMSM驱动电流为正弦波,相对无刷直流电机而言,其具有功率大、控制精度高、噪声小、转动惯量小等优势,且其参数不受电机极对数影响,便于实现电机直接驱动负载,特别适合用作电动汽车轮毂电机[1-3]。
目前常用的PMSM控制策略包括矢量控制和直接转矩控制[4]。传统矢量控制一般使用PI线性调节器对转速和电流进行调节,当电机内部参数发生变化以及外界扰动量大时,传统PI调节参数无自整定功能难以跟随电机工况变化,易出现超调、抗负载能力弱等情况[5]。传统直接转矩控制利用滞环比较器(也叫Bang-Bang控制器)直接调节定子磁链和转矩,具有控制结构简单、响应速度快等优点;但由于低速定子磁链估算精度低、逆变器开关频率不稳定、电压矢量和磁链阶跃式变化等因素,系统低速转矩脉动明显[6]。
针对上述两种控制策略的缺点,国内外学者引入了许多先进的控制理论对其进行改善,如模糊控制[7-8]、神经网络控制[9-10]、自抗扰控制[11-12]、模型预测控制[13-14]、反推控制[15-16]、自适应控制[17-18]和滑模变结构控制[19-20]等。笔者选取模糊理论和Super-twisting二阶滑模算法分别对矢量控制和直接转矩控制进行优化,并根据Matlab/Simulink建模仿真结果对比分析各种策略的控制特性,为电动汽车电机控制方案的选择提供理论依据。
1 PMSM的数学模型
PMSM是一个非线性、强耦合、高阶、多变量的复杂系统,为简化分析,现作如下假设[6]:
(1)转子没有阻尼绕组;
(2)电机铁心是线性的,忽略饱和效应,不考虑涡流及磁滞耗损;
(3)定子三相绕组对称分布,定子电流呈正弦波形,气隙中有且仅有正弦分布磁势;
(4)气隙中永磁体磁场呈正弦分布,不存在高次谐波。
在自然坐标系下,PMSM的动态数学模型由式(1)所示的电压、磁链、转矩和运动方程构成。
(1)
式中:us、Rs、is、ψs、Ls分别为定子三相绕组的电压、电阻、电流、磁链和电感;φf为永磁体磁链;Fs(·)为三相绕组的磁链;Te为电机的电磁转矩,可根据机电转换原理求得;p为电机极对数;θm为电机转子机械位置角;ωm为转子机械角速度;J为转动惯量;TL为负载转矩;B为阻尼系数。
通过Clark变换与Park变换可得两相旋转坐标系d-q下的数学模型,其定子电压方程为:
(2)
磁链方程为:
(3)
将式(3)带入式(2)容易得到:
(4)
电磁转矩方程为:
Te=1.5pid[id(Ld-Lq)+φf]
(5)
式中:ud、id、φd分别为定子电压、电流和磁链的d轴分量;uq、iq、φq为q轴分量;ωe为电角速度;Ld、Lq分别为电感的d、q轴分量。
2 矢量控制及优化
2.1 矢量控制基本原理
传统矢量控制[21](field-oriented control,FOC)借鉴直流电机解耦控制思想,以坐标变换理论为基础,通过控制电机定子电流交、直轴分量的大小及相位,完成转矩与磁链的解耦控制。当采用id=0的控制方式时,三相PMSM的FOC原理如图1所示。
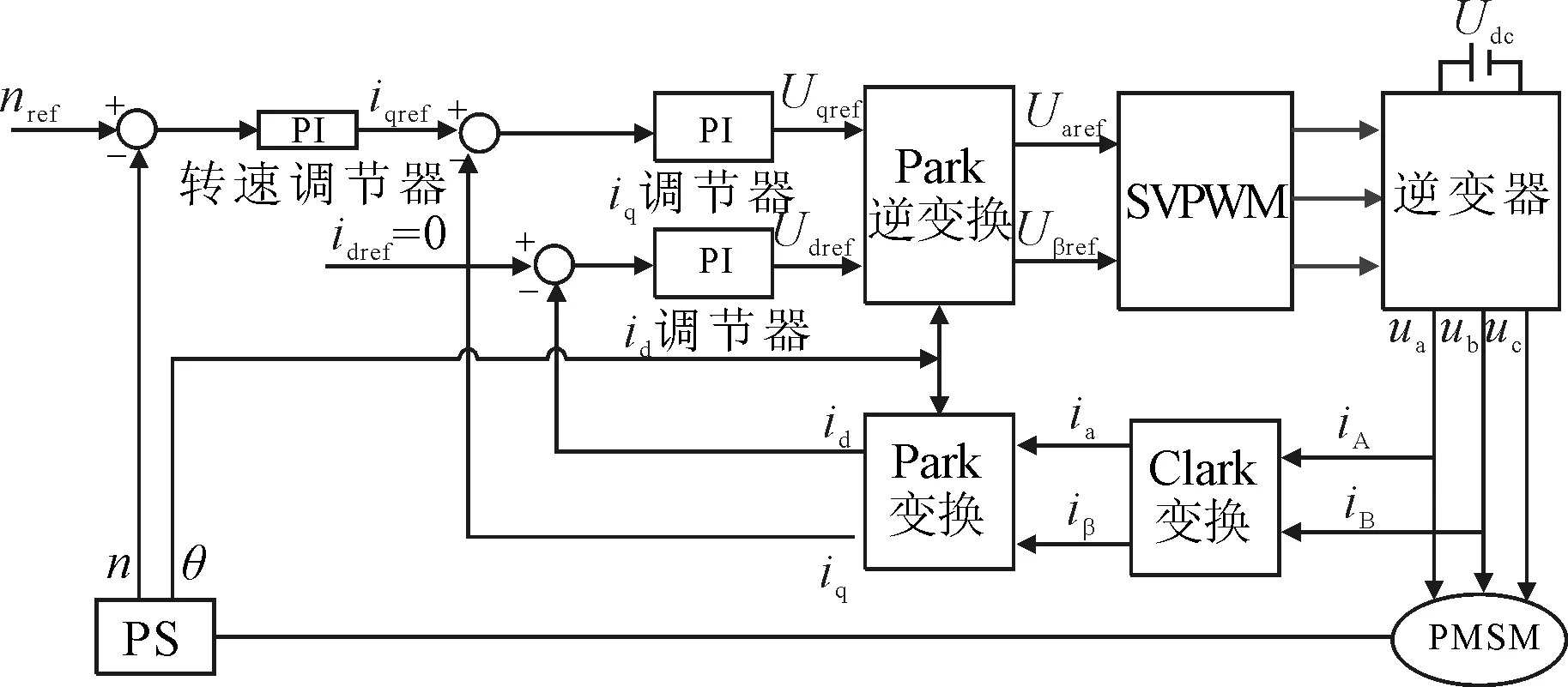
图1 三相PMSM id =0的矢量控制原理图
由图1可知,矢量控制系统主要由一个转速外环、两个电流内环以及空间脉宽矢量调制(space vector PWM, SVPWM)算法几部分构成。其中,转速环用于调节电机转速,使系统具有快速响应和保持稳态运行的能力;电流环用于缩短系统动态调节时间,使三相定子电流能够更好地跟随正弦参考波。转速环与电流环均使用PI调节器,而传统PI的参数值是固定的,无自整定功能。因此,当电机参数变化和负载变化超过原有PI参数的调节范围时,系统将难以跟随工况变化,易出现超调或抗负载扰动性能差等现象,从而影响电机控制性能。
2.2 基于模糊PI的FOC优化策略
2.2.1模糊PI控制基本原理
针对传统PI参数无法实时调节的弊端,笔者选取模糊理论对图1中速度环PI调节器进行改进,使PI参数能够自行调节。模糊PI控制器将实际转速n与给定转速nref的偏差e和偏差变化率ec作为输入变量,对其进行模糊化、模糊推理以及解模糊处理后得到PI控制参数的实时调整量ΔKp、ΔKi,及时修正PI控制器参数,其系统结构如图2所示[22]。调整后控制器参数Kp、Ki满足:Kp=Kp0+ΔKp,Ki=Ki0+ΔKi。其中,Kp0、Ki0为原传统PI调节器给定的参数值。
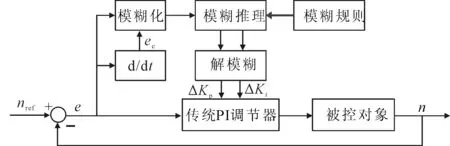
图2 模糊PI控制器系统结构
2.2.2模糊控制器设计
由图2可知,模糊控制器求解过程分三步进行:模糊化、模糊推理和解模糊。
(1)模糊化。模糊化是把变量从精确的数字量转变为模糊量的过程,具体步骤如下[23]:
①输入输出变量选择。由2.2.1可知,控制器的输入变量为e、ec,输出变量为ΔKp、ΔKi,故控制器类型应该选择二维的。
②模糊化语言变量确定。根据输入、输出变量的实际变化情况,采用模糊化语言变量“负大、负中、负小、零、正小、正中、正大”来描述变化的方向和大小,一般表示为{NB,NM,NS,ZO,PS,PM,PB}。
③基本论域、模糊论域、量化因子、比例因子选取。基本论域界定变量的实际变化范围;模糊论域界定模糊语言变量的范围:量化因子、比例因子分别描述输入、输出变量的模糊化程度。这里取e、ec的模糊论域为[-3,3];ΔKp、ΔKi的模糊论域为[-6,6];量化因子Ke、Kec分别为0.001 5、0.000 3;比例因子Kup、Kui分别为0.11、0.18;e、ec、ΔKp、ΔKi基本论域分别为[-2 000,2 000]、[-10 000,10 000]、[-0.33,0.33]、[-0.54,0.54]。
④定义各变量的隶属度函数。Matlab的Fuzzylogic工具箱提供了多种可供选择的隶属度函数,包括三角形、梯形、钟形、高斯形和π形等。笔者选择常用的三角函数作为各模糊语言变量的隶属度函数。
(2)模糊推理。模糊推理是将经过模糊化处理的输入变量,按照模糊控制规则,找到与之对应的模糊输出量的过程,其核心是建立模糊控制规则。规则制定应满足以下原则:①当e和ec较大时,取大的Ku,以缩短系统的过渡时间;②当e和ec较小时,取小的Ku,以约束系统的超调,使其快速进入稳态。根据专家实际工程实践经验和知识,结合多组仿真实验结果得到ΔKp和ΔKi的模糊控制规则如表1所示[8]。

表1 ΔKp/ΔKi模糊控制规则表
根据模糊规则表就可以编写“IF…THEN…”形式的模糊推理语句,从而找到与输入模糊量相对应的输出模糊量。例如:“IFeis NB andecis NB, THEN ΔKpis PB and ΔKiis NB”。
(3)解模糊。经过模糊推理所得的输出变量是模糊量,需经过解模糊处理转变为数字量才能用到被控对象上。解模糊的方法有多种,如加权平均法、重心法、最大隶属度法等,笔者选择精度最高的重心法进行输出变量解模糊计算。
根据以上分析,在Matlab命令窗口中键入“Fuzzy”,调用FIS编辑器,设计转矩模糊控制器,并将其嵌入到PI控制器Simulink仿真模型中,构成完整的模糊PI控制器仿真模型,如图3所示。
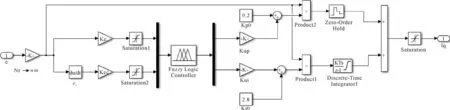
图3 模糊PI速度控制器仿真模型
3 直接转矩控制及优化
3.1 直接转矩控制基本原理
直接转矩控制[24](direct torque control, DTC)最早是由I.Takahash与T.Noguchi共同提出的,其基本思想是:以定子磁链定向为基础,通过控制定子磁链的幅值及负载角(定子磁链与转子磁链之间的夹角)来控制电机的转矩和磁链,摒弃了传统矢量控制的解耦思想,无需进行坐标变换,简化了控制系统结构,提高了系统的控制运算速度和鲁棒性,其系统结构如图4所示。

图4 三相PMSM传统DTC系统结构
由图4可知,传统DTC将逆变器与电机控制策略进行一体化设计,没有单独的PWM控制器,逆变器功率器件开关的导通与关断由磁链及转矩滞环比较器的输出结果分扇区控制。而转矩滞环比较器的容差值大小会直接影响转矩脉动的大小,容差值越小转矩脉动越小,但即便将容差值设为零,转矩脉动仍旧很大。且由电机的磁链方程可将磁链近似为电压的积分,而电压矢量在电机运行过程中是阶跃式变化的,故磁链随之阶跃变化,从而引起转矩脉动。此外,低速时转速测量精度和定子磁链估算精度低也会引起电机转矩脉动。综上,传统DTC最大的缺点是转矩脉动明显。
3.2 基于Super-twisting滑模的DTC优化策略
针对传统DTC存在低速转矩脉动大的缺点,将其改为基于SVPWM算法的DTC,同时采用具有动态响应快、抗干扰能力强、鲁棒性好的Super-twisting二阶滑模控制理论设计滑模控制器,取代原来的滞环比较器,改善系统控制性能,改进后的系统结构如图5所示[25]。
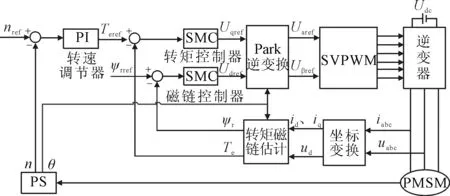
图5 基于Super-twisting滑模的SVPWM-DTC控制系统结构
3.2.1Super-twisting滑模控制基本原理
一般地,非线性动态系统可以描述为[26]:
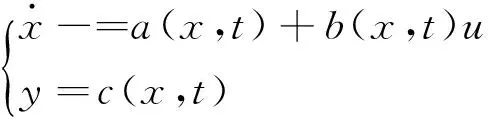
(6)
式中:x、u、y分别为系统的状态变量、输入控制变量、输出变量;a(x,t)、b(x,t)为连续、未知的滑模变量函数;c(x,t)为滑模面函数,若系统中的点运动到滑模面c(x,t)=0的时间都是有限的,则只要输入变量有界系统就能在有限时间内收敛,即满足可达性要求。
上述系统的二阶滑模控制器的通式为[27]:
(7)
式中:sgn(·)为符号函数;|y|为y的模,r、k1、k2、k3、k4和KA、KB均为设计参数,且KA、KB< 0,r>0。对Super-twisting控制器有:k1=k4=0,故Super-twisting滑模的控制律可表示为一个不连续的滑动变量函数和一个连续的导数函数,如式(8)所示:
(8)
为满足滑模运动的可达性和稳定性要求,式(8)中的增益系数Kp、Ki必须取得足够大,Kp、Ki之间存在如下关系[28]:
(9)
式中,|Am|≥A,Bm≥B≥Bn,且A、B的值由式(10)确定:
(10)
两个微分方程对应的系数A、B均是关于电机电流、电感、转速、转动惯量、磁链、极对数等参数的一次函数,这些参数的值都是有限的,故系统是有界的。
3.2.2Super-twisting滑模控制器设计
首先,定义磁链与转矩的滑模面函数如下:
(11)

根据Super-twisting滑模控制基本原理,得到磁链控制器的表达式为:
(12)
同理,转矩控制器的表达式为:
(13)
式中,Kp、Ki应满足式(9)和式(10)的可达性和稳定性要求。当r=0.5时,可得到能在有限时间收敛的控制器,其仿真模型如图6所示。

图6 r=0.5的Super-twisting滑模控制器仿真模型
4 仿真结果与分析
为验证所建模型的正确性,分析各种策略的控制性能,在Matlab/Simulink中建立上述控制策略仿真模型,结合情景分析法,采用表2、表3的电机及控制系统参数进行不同情景下的仿真。
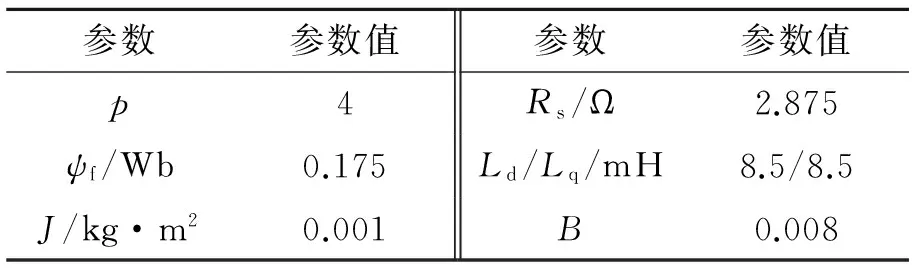
表2 PMSM仿真参数

表3 PMSM控制系统仿真参数
情景1:电机转速n=1 000 r/min,t=0 s时负载TL=0 N·m;t=0.15 s时负载突变为5 N·m;
情景2:电机转速n=500 r/min,t=0 s时负载TL=0 N·m;t=0.15 s时负载突变为2 N·m;
情景3:电机转速n=100 r/min,t=0 s时负载TL=0 N·m;t=0.15 s时负载突变为2 N·m。
图7~图9分别为仿真情景1、2、3下FOC及其优化控制策略的转速、转矩仿真结果。从图7(a)~图9(a)可以看出:采用模糊PI的FOC(简写为Fuzzy-FOC,下同)与采用传统PI的FOC相比,在超调量方面,前者的转速超调量几乎为0,后者约为6.18%;在系统响应时间上,前者初次达到转速给定值的时间约为0.012 8 s,响应速度较后者慢,这是模糊PI控制器为减小系统超调量而减小比例系数Kp使得系统调节速度减慢引起的;在系统突加负载的情况下,Fuzzy-FOC掉速更慢,且恢复稳态的速度更快,系统的稳定性更好。从图7(b)~图9(b)可以看出:Fuzzy-FOC与 FOC都是以最大转矩起动的,二者在各转速下的转矩脉动均比较小,在参考值±0.175 N·m的范围内波动。
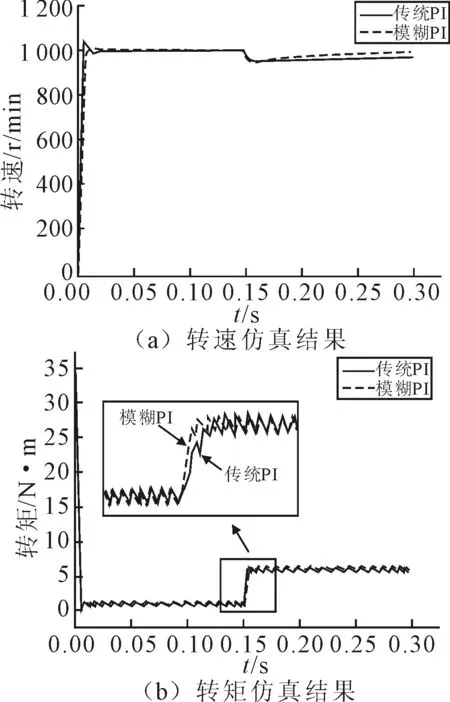
图7 情景1下FOC与Fuzzy-FOC转速、转矩仿真结果

图8 情景2下FOC与Fuzzy-FOC转速、转矩仿真结果

图9 情景3下FOC与Fuzzy-FOC转速、转矩仿真结果
图10~图12分别为仿真情景1、2、3下DTC及其优化控制策略的转速、转矩仿真结果。从图10(a)~图12(a)可以看出:基于Super-twisting滑模的SVPWM-DTC(简写为STSM-DTC,下同)与传统DTC相比,在超调量方面,二者在中高速(情景1和情景2)下均无超调,调速精准,低速(情景3)时传统DTC转速调节能力较差,一直在给定转速周围波动,难以进入稳态,而STSM-DTC能快速进入稳态;在系统响应时间上,STSM-DTC在各转速下的响应均很快,初次达到给定转速的时间约为0.004 9 s,DTC约为0.012 6 s,前者比后者快61.1%;当系统突加负载时,STSM-DTC转速变化很小,且能快速回复到稳定状态,而DTC抵抗负载突变能力相对较差,尤其是在低速条件下。从图10(b)~图12(b)可以看出:STSM-DTC与DTC都是以最大转矩起动的,前者响应速度快于后者;二者的转矩脉动均随着转速的降低而逐渐变大,在情景3下二者的转矩脉动最大,前者脉动量约为±0.122 N·m,仅为后者的22.7%。

图10 情景1下传统DTC与STSM-DTC转速、转矩仿真结果

图11 情景2下传统DTC与STSM-DTC转速、转矩仿真结果

图12 情景3下传统DTC与STSM-DTC转速、转矩仿真结果
对图7~图12的仿真结果进行统计,可得到如表4所示的各种控制策略的控制性能。
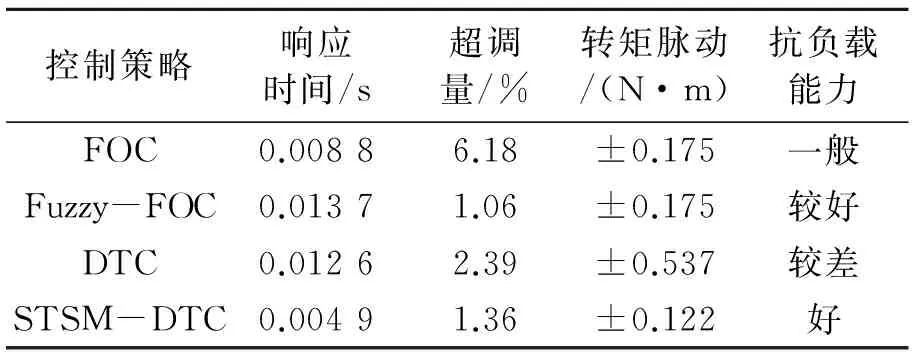
表4 各种控制策略的控制性能对比
由表4可知,综合控制性能最佳的控制策略为STSM-DTC,其调速精准、响应速度快、抗负载能力强,且明显降低了传统DTC的转矩脉动,在全速范围内均能维持良好的动、静态控制性能,适合选作直驱式轮毂电机的控制策略。其次是Fuzzy-FOC,其响应速度虽然较其他控制策略慢,但仍然比车辆机械系统响应速度快了很多,完全能满足车辆对电机响应速度的要求,且Fuzzy-FOC转矩脉动小,明显改善了使用传统PI调节器的FOC超调量大的缺点,抗负载能力也有所提高,但低速控制性能较差,适用于减速驱动式轮毂电机控制系统。FOC虽然有明显的超调,但可以通过调节PI参数减小超调量,且其转矩脉动小,调速范围较宽,可用于控制带减速器的驱动电机。传统DTC低速转矩脉动大,若电机长期处于低速运行工况下,则电机的振动和噪声会很大,不仅会影响整车的NVH性能,还会造成污染和伤害;且传统DTC抵抗负载突变的能力较差,在负载频繁变化的工况下电机将很难满足工况需求,因此,传统DTC不适合用来控制电动乘用车和电动公交车等长期在城市工况下运行的电动汽车的驱动电机,可用作长途运输的电动商用车驱动电机控制策略。
5 结论
(1)采用模糊控制理论优化后的Fuzzy-FOC相比采用传统PI的FOC在中高速条件下,系统超调量降低了约4.12%,系统进入稳态的调节时间有所减少,抗负载能力也有所改善,但低速控制性能无明显改善。
(2)采用Super-twisting滑模控制理论优化后的STSM-DTC相比采用传统的DTC系统响应速度快,响应时间约为0.004 9 s,比后者快61.1%;前者在全速范围内均能快速进入稳态,抵抗负载干扰能力明显优于后者;前者转矩脉动得到明显改善,在低速(100 r/min)条件下,其转矩脉动量约为±0.122 N·m,较后者降低了77.3%。
(3)对比优化前后的4种控制策略,综合控制性能最佳的是STSM-DTC,其在全速范围内均能保持良好的动、静态控制性能,适合选作直驱式轮毂电机的控制策略;其次是Fuzzy-FOC,其低速控制性能较差,适用于减速驱动式轮毂电机控制系统;FOC更适用于控制带减速器的驱动电机;传统DTC可用作长途运输的电动商用车驱动电机控制策略。
参考文献:
[1]张之超,邹德伟.新能源汽车驱动电机与控制技术[M].北京:北京理工大学出版社,2016.
[2]袁登科,陶生桂.交流永磁电机变频调速系统[M].北京:机械工业出版社,2011.
[3]Haque M E. Permanent Magnet Synchronous Motor Drives[M].[S.l.]: VDM Verlag Dr. Müller, 2009.
[4]刘红伟.永磁同步电机控制策略及算法融合研究[D].成都:中国科学院研究生院,2014.
[5]王贤会,李宝营,冯荻.基于模糊自适应的永磁同步电机矢量控制系统[J].大连工业大学学报,2017,36(3):227-230.
[6]王军.永磁同步电机智能控制技术[M].成都:西南交通大学出版社,2015.
[7]Zhao Y, Huang Z. Fuzzy Direct Torque Control of Permanent Magnet Synchronous Motors[C]∥ International Conference on Fuzzy Systems and Knowledge Discovery of the IEEE.[S.l.]:IEEE, 2016:330-334.
[8]李爱平,邓海洋,徐立云.基于模糊PID的永磁同步电机矢量控制仿真[J].中国工程机械学报,2013,11(1):25-30.
[9]叶德住.基于BP神经网络的永磁同步电机控制[J].微电机,2016,49(11):57-61.
[10]Zare J. Vector Control of Permanent Magnet Synchronous Motor with Surface Magnet Using Artificial Neural Networks[C]∥ 2008 International Conference of Universities Power Engineering of the IEEE. [S.l.]: IEEE, 2008:1-4.
[11]Wen J, Huang Y. Robust Speed Control of Permanent Magnet Synchronous Motor[C]∥ Industrial Electronics and Applications of the IEEE. [S.l.]: IEEE, 2013:327-330.
[12]祁世民,周臻,窦晓华,等.基于自抗扰控制的PMSM直接转矩控制研究[J].微特电机,2017,45(2):42-45.
[13]高旭东,许鸣珠,栾东雪.基于Kautz模型的永磁同步电动机调速系统电流预测控制[J].微特电机,2016,44(9):78-82.
[14]Liu M, Hu J, Chan K W. Improved Model Predictive Control of Permanent Magnet Synchronous Motor with Duty Ratio Optimization and Cost Function Correction[C]∥ International Conference on Electrical Machines and Systems. [S.l.]: [s.n.],2017:1-5.
[15]Rudra S, Barai R K, Maitra M, et al. Robust Adaptive Integral Backstepping Control and Its Implementation on Permanent Magnet Synchronous Motor[C]∥ India Conference of the IEEE. [S.l.]: IEEE, 2013:1-6.
[16]王家军.速度指定位置跟踪双永磁同步电动机的反推控制[J].控制理论与应用,2015,32(2):202-209.
[17]Bernat J, Kolota J, Stepien S, et al. Adaptive Control of Permanent Magnet Synchronous Motor with Constrained Reference Current Exploiting Backstepping Methodology[C]∥ Control Applications of the IEEE. [S.l.]: IEEE, 2014:1545-1550.
[18]Li L. Adaptive Fuzzy Back-stepping Control System of Permanent Magnet Synchronous Motor[C]∥ Control and Decision Conference of the IEEE. [S.l.]: IEEE, 2017:581-584.
[19]李中琴.基于新型变速趋近律的永磁同步电机滑模控制[J].电机与控制应用,2017,44(5):22-26.
[20]Lascu C, Boldea I, Blaabjerg F. Super-twisting Sliding Mode Control of Torque and Flux in Permanent Magnet Synchronous Machine Drives[C]∥ 2013 Conference of Industrial Electronics Society of the IEEE. [S.l.]: IEEE, 2014:3171-3176.
[21]陈修亮,车倍凯.永磁同步电机矢量控制解耦方法的研究[J].电气技术,2013(4):37-40.
[22]卞延庆,庄海,张颖杰.基于模糊PI的永磁同步电机矢量控制研究[J].微电机,2015,48(11):62-66.
[23]Zdenko K, Stjepan B.模糊控制器设计理论与应用[M].胡玉玲,译.北京:机械工业出版社,2010.
[24]Takahashi I, Noguchi T. A New Quick-response and High-efficiency Control Strategy of an Induction Motor[J]. IEEE Transactions on Industry Applications, 1986,22(5):820-827.
[25]杨鑫,迟长春,耿晋中,等.基于Super-twisting控制器的永磁同步电动机无传感器直接转矩控制[J].上海电机学院学报,2017,20(3):139-146.
[26]唐翱.基于Super-twisting滑模的永磁同步电机直接转矩控制的研究[D].郑州:郑州大学,2016.
[27]Gennaro S D, Rivera J, Castillo-Toledo B. Super-twisting Sensorless Control of Permanent Magnet Synchronous Motors[C]∥ Decision and Control of the IEEE. [S.l.]: IEEE, 2010:4018-4023.
[28]潘月斗,陈涛,陈泽平.感应电机 Super-twisting 算法定子磁链观测器设计[J].电机与控制学报,2016,20(5):60-67.
