Cr12MoV钢动态再结晶过程的元胞自动机模拟

陈森林，廖敦明，滕子浩，陈涛



Cr12MoV钢动态再结晶过程的元胞自动机模拟

陈森林，廖敦明，滕子浩，陈涛

(华中科技大学 材料成形与模具技术国家重点实验室，湖北 武汉，430074)

利用Gleeble−3500多功能热力模拟试验机，研究Cr12MoV钢在应变温度为1 050~1 150 ℃及应变速率为0.01~10 s−1变形条件下的动态再结晶行为，利用回归分析结果，建立元胞自动机模型模拟Cr12MoV钢的动态再结晶过程。研究结果表明：Cr12MoV钢的再结晶激活能act为458.069 kJ/mol；模拟得到的再结晶晶粒粒径平均值与实验得到的结果相对误差在10.2%内；模拟预测的应力应变曲线能够较好地反映再结晶过程应力应变曲线特点，与实验值相符合，峰值应力最大相对误差在3.9%内；在一定应变范围内，再结晶晶粒粒径和再结晶分数随着应变的增加而增加；应变速率越大，再结晶过程越不充分，随着应变增加，获得的再结晶晶粒更小。

元胞自动机；动态再结晶；材料计算科学；组织模拟

动态再结晶(dynamic recrystallization, DRX)是金属在热变形过程中发生的一种冶金物理现象，它是决定成形后最终微观组织和力学性能的重要因素。在工业生产上，通过制定合理的工艺，充分利用金属的动态再结晶过程，获得细小均匀的组织，能有效提高产品的质量。因此，动态再结晶微观组织的演变过程的模拟研究尤为重要。随着材料计算科学和计算机硬件的不断进步，集成计算材料工程(integrated computational materials engineering，ICME)得到了长足的发展，对材料微观组织在不同尺度上的理论建模和模拟也更加成熟。就介观尺度而言，蒙特卡洛法(Monte Carlo)、相场法(phase field, PF)和元胞自动机法(cellular automata , CA)成为研究再结晶过程微观组织演化的主要方法。GOETZ等[1]提出了动态再结晶过程的CA模型。DING等[2]结合金属冶金学理论和CA法，成功模拟了再结晶过程中晶粒形核和长大的过程，并且与实验结果较符合。KUGLER等[3]利用CA法模拟了多道次DRX过程，分析了变形条件对再结晶过程的影响。肖宏等[4]提出了一种考虑再结晶晶粒变形的元胞自动机模型；关小军等[5]建立了考虑粒子阻碍效应的动态再结晶CA模型，并且模拟结果与实验结果相符度高。本文作者构建Cr12MoV钢动态再结晶过程的CA模型，并且与实验结果对比，描述了Cr12MoV钢的动态再结晶行为。

1 模拟模型的建立

1.1 元胞自动机模型

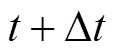
为了简化模型，采用以下假设[2]：

1) 母体中的位错密度均一，动态再结晶晶粒的位错密度在0和饱和位错密度之间变化。位错密度达到临界值才会发生动态再结晶，发生动态再结晶晶粒的位错密度再次达到临界值时可发生新一轮的动态再结晶，只有再结晶次数大的晶粒可以吞噬再结晶次数较低的晶粒。

2) 再结晶晶粒形核只发生在晶粒边界(包括母体晶界和动态再结晶的晶界)。

3) 对组织进行简化，认为材料内部无织构，晶粒内无缺陷。

4) 再结晶晶粒内的位错密度均一，没有位错 梯度。

1.2 形核模型

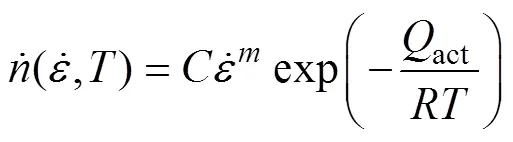
式中：为常数，可通过实验或反分析法[6]确定；为常数，在本文中取1；act为动态再结晶变形激活能，J/mol；为理想气体常数；为变形温度，K。

1.3 位错密度增长模型

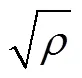
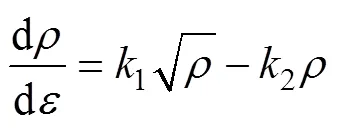
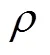
1.4 再结晶晶粒生长模型

动态再结晶晶粒形核后，新生的再结晶晶粒内较低的位错密度和母体的高位错密度之间的差值，为再结晶晶粒的长大提供了驱动力。晶粒的长大速度与单位面积上的驱动力成正比[9]：

对于半径为r的动态再结晶晶粒，其驱动力为[11]

1.5 实验材料与方法

实验选用的Cr12MoV钢化学成分如表1所示，试样直径×长度为8 mm×12 mm的圆柱体。将试样在Gleeble−3500热模拟实验机上进行热压缩实验[13]，实验工艺如图1所示，先以5 ℃/s的速度加热到1 230 ℃，保温3 min，然后以2 ℃/s的速度降低到变形温度，保温1 min后开始压缩，变形完毕后淬火。将变形后的试样沿轴线切开，经过镶样、研磨、抛光后用4%的硝酸酒精腐蚀1 min，在金相显微镜下观察晶粒形貌并拍照。

表1 Cr12MoV钢化学成分(质量分数)

图1 Cr12MoV钢热压缩试验工艺

1.6 材料激活能及其本构方程的确定

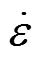
从图2可以看出：Cr12MoV钢的流变应力曲线具有较明显的动态再结晶特征，即随着应变的增加，流变应力先增加至某一峰值后开始缓慢降低，最终达到稳态值。

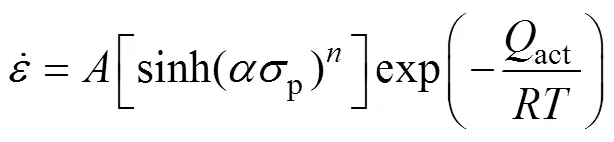
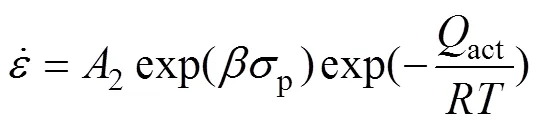
对式(7)，(8)，(9)分别取对数，可得：

本模拟使用Cr12MoV材料参数如表2所示。

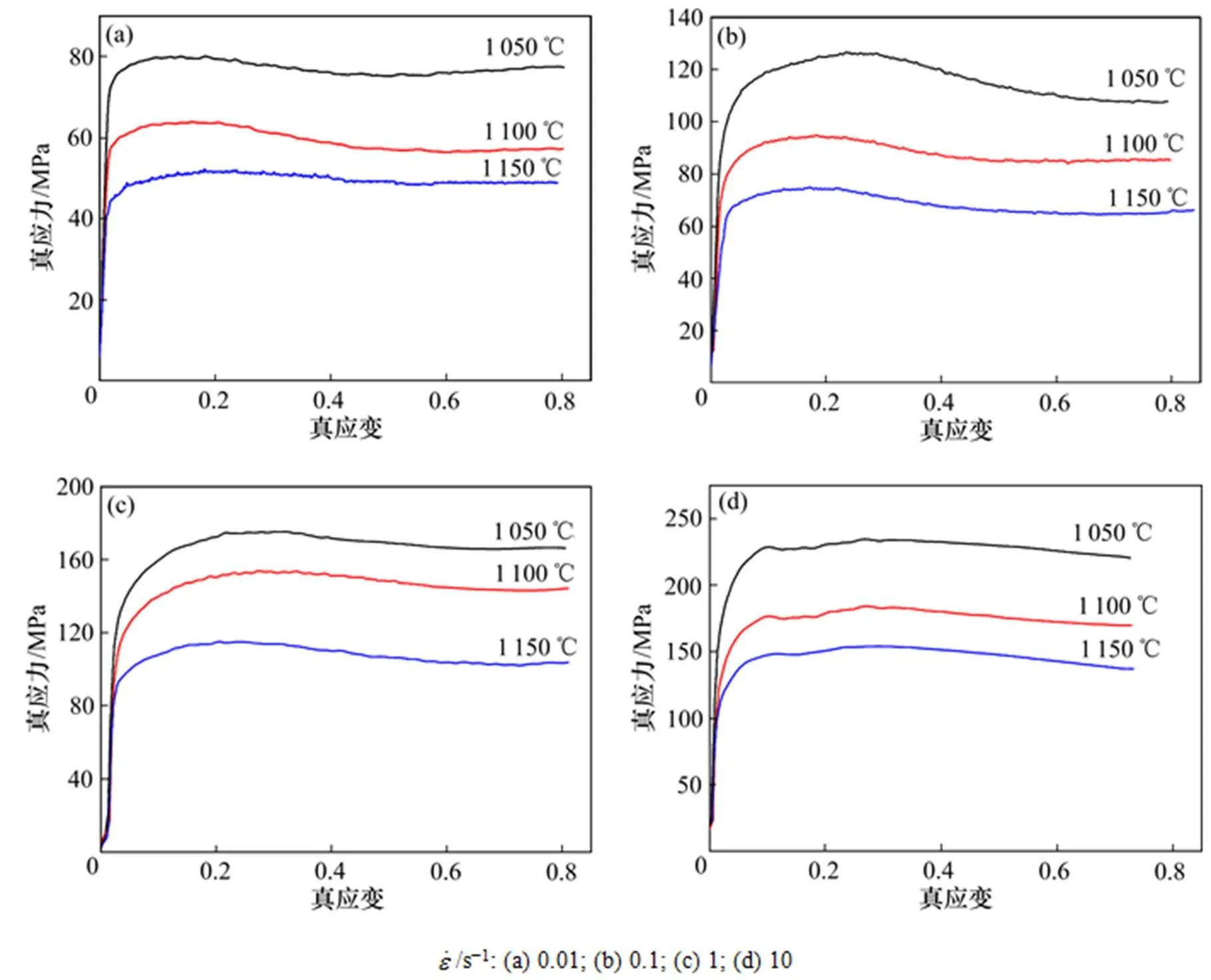
图2 Cr12MoV钢热压缩应力−应变曲线

图3 关系图

图4 关系图

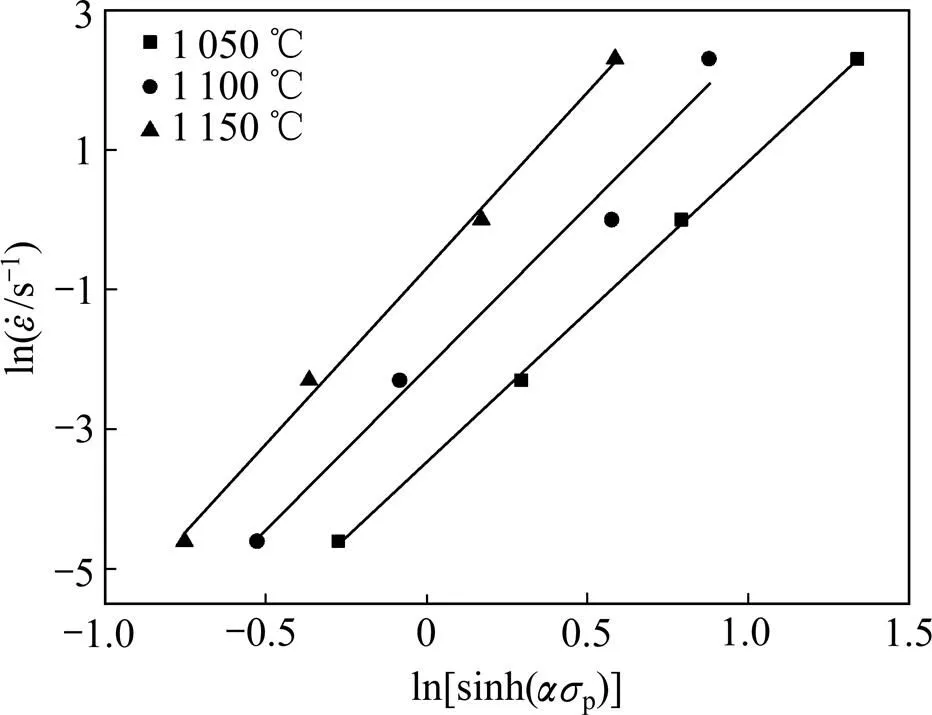
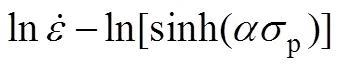
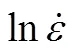
图6 关系图

表2 Cr12MoV钢材料参数

式中：为Zener−Hollomon参数，即温度补偿的应变速率因子，s−1。

对式(14)两边求对数得：

对作图并回归分析，结果如图7所示，得截距，因此，A=3.16×1016。

故Cr12MoV钢的动力学方程为

Cr12MoV钢的本构方程为

2 结果分析

将求得的激活能act及相关参数代入CA模型，编制程序并输出相关结果。应变为0.8，不同变形条件下程序模拟结果与实验获得的晶相组织对比如图8所示。

从图8可以发现：Cr12MoV钢在温度为1 150 ℃的条件下变形后，晶粒形貌并未出现变形织构，以细小均匀的等轴晶为主，即发生了明显的动态再结晶过程，且应变速率越大，获得的等轴晶粒平均粒径就越小；而应变速率相同时，变形温度越高，获得的再结晶等轴晶粒粒径就越大。模拟得到的微观组织形貌轮廓清晰，可分辨度高，其晶粒形貌与金相图片相似。运用截线法测定的平均晶粒粒径与CA法统计的平均晶粒粒径结果比较见表3。从表3可见：平均晶粒粒径相对误差在 10.2%内，即元胞自动机模拟结果能够正确描述动态再结晶规律并较准确地预测其晶粒粒径。

图9所示为使用CA法得出的变形温度为1 150 ℃条件下，不同变形速率对应的应变和再结晶分数之间的关系。从图9可以看出：动态再结晶分数随着应变的增加而增加，且当应变速率较小时，动态再结晶能够更早发生，且完成得更快。

图8 不同变形条件下CA模拟获得的动态再结晶组织与实验结果对比

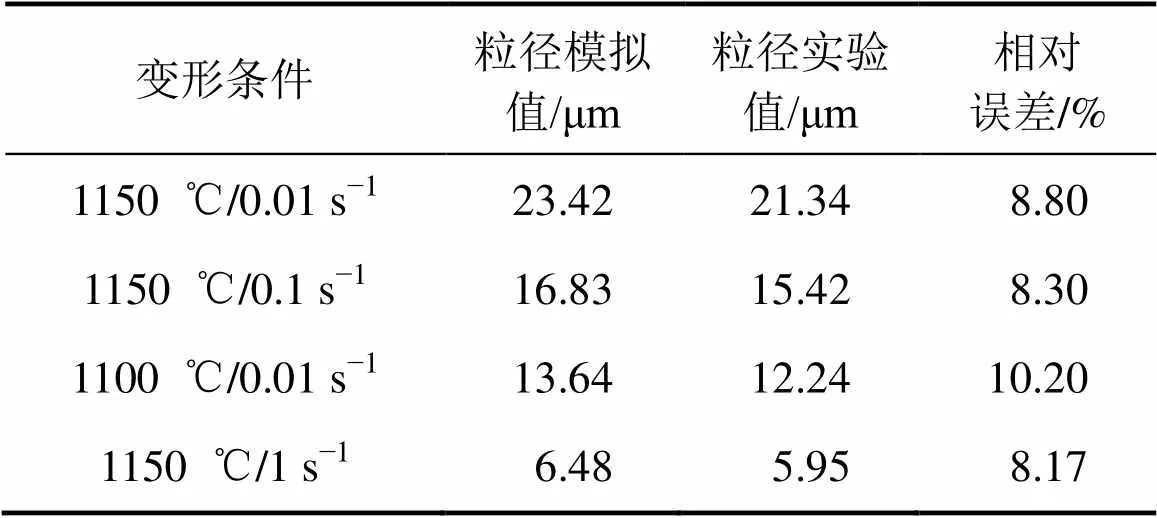
表3 各变形条件下再结晶晶粒粒径试验值与模拟值比较

图9 在温度为1 150 ℃、不同变形条件下应变与再结晶分数之间的关系

在变形温度为1 050 ℃条件下，运用CA法根据平均位错密度计算出不同应变率条件下的流变应力曲线与实验值的对比如图10所示。由图10可见：流变应力模拟结果与实验值相对误差在3.9%以内，相符度较好，体现了实际应力应变曲线的特征：流变应力随着应变的增加而快速升高，达到峰值后略有降低，最终区域稳定值。从而进一步验证了CA模型的正确性。

图10 变形温度为1 050 ℃时不同变形速率下模拟和实验的应力−应变曲线对比

3 结论

2) 元胞自动机模型能够较好地模拟Cr12MoV动态再结晶过程晶粒粒径和再结晶分数变化，其中晶粒粒径相对误差在10.2%内。模拟获得的流变应力应变与实验值相符度较高。

3) 元胞自动机能正确揭示应变、应变速率对晶粒大小及再结晶分数的影响：在一定应变范围内，再结晶晶粒粒径和再结晶分数随着应变的增加而增加；应变速率越大，再结晶过程越不充分，随着应变增加，获得的再结晶晶粒更小。

[1] GOETZ R L, SEETHARAMAN V. Modeling dynamic recrystallization using cellular automata[J]. Scripta Materialia, 1998, 38: 405−413.

[2] DING R, GUO Z X. Microstructural modelling of dynamic recrystallisation using an extended cellular automaton approach[J]. Computational Materials Science, 2002, 23(1): 209−218.

[3] KUGLER G, TURK R. Modeling the dynamic recrystallization under multi-stage hot deformation[J]. Acta Materialia, 2004, 52: 4659−4668.

[4] 肖宏, 徐玉辰, 闫眼红. 考虑晶粒变形动态再结晶过程模拟的元胞自动机法[J]. 中国机械工程, 2005, 16(24): 2245−2248. XIAO Hong, XU Yuchen, YAN Yanhong. Cellular automaton method for simulation of dynamic recrystallization process with consideration of grains deformation[J]. China Mechanical Engineering, 2005, 16(24): 2245−2248.

[5] 关小军, 麻晓飞. 考虑粒子阻碍效应的再结晶元胞自动机模型[J]. 东北大学学报(自然科学版), 2014, 35(8): 1141−1154. GUAN Xiaojun, MA Xiaofei. Modeling of recrystallization for material with precipitated fine particles by cellular automaton method[J]. Journal of Northeastern University (Natural Science), 2014, 35(8): 1141−1154.

[6] 金朝阳. 基于反分析法的热变形低碳钢动态再结晶行为数值模拟[D]. 上海: 上海交通大学材料科学与工程学院. 2010: 44−54. JIN Zhaoyang. Modelling and simulation of dynamic recrystallization for hot deformed low carbon steel by inverse analysis method[D]. Shanghai: Shanghai Jiao Tong University. College of Material Science and Engineering, 2010: 44−54.

[7] MECKING H, KOCKS U F. Kinetics of flow and strain- hardening[J]. Acta Metallurgica, 1981, 29(11): 1865−1875.

[8] ZHANG Yanqiu, JIANG Shuyong, LIANG Yulong, et al. Simulation of dynamic recrystallization of NiTi shape memory alloy during hot compression deformation based on cellular automaton[J]. Computational Materials Science, 2013, 71(13): 124−134.

[9] JI H P, ZHANG L G, LIU J, et al. Microstructure prediction of 316ln stainless steel for dynamic recrystallization based on cellular automata[J]. Key Engineering Materials, 2016, 693: 674−679.

[10] CHEN Fei, CUI Zhenshan, LIU Juan, et al. Modeling and simulation on dynamic recrystallization of 30Cr2Ni4MoV rotor steel using the cellular automaton method[J]. Modelling and Simulation in Materials Science and Engineering, 2009, 17(7): 075015-1−075015-19.

[11] YANG He, WU Chuan, LI Hongwei, et al. Review on cellular automata simulations of microstructure evolution during metal forming process: grain coarsening, recrystallization and phase transformation[J]. Technological Sciences, 2011, 54(8): 2107−2118.

[12] SHAHRANI A AL, YAZDIPOUR N, DEHGHAN-MANSHADI A. The effect of processing parameters on the dynamic recrystallization behavior of API-X70 pipeline steel[J]. Materials Science & Engineering A, 2013, 570: 70−81.

[13] HUANG S, WANG L, ZHANG B, et al. Hot deformation behavior and microstructure evolution of GH4706 alloy[J]. Journal of Materials Engineering, 2015, 43(2): 41−46.

[14] KIM H Y, HONG S H. High temperature deformation behavior and microstructural evolution of Ti-47Al-2Cr-4Nb intermetallic alloys[J]. Scripta Materialia, 1998, 38(10): 1517−1523.

[15] NIE J F. Preface to viewpoint set on: phase transformations and deformation in magnesium alloys[J]. Scripta Materialia, 2003, 48(8): 981−984.

[16] ZENER C, HOLLOMON J H. Effect of strain rate upon the plastic flow of steel[J]. J Appl Phys, 1994, 15(1): 22−32.

(编辑 赵俊)

Dynamic recrystallization simulation of Cr12MoV steel using cellular automation method

CHEN Senlin, LIAO Dunming, TENG Zihao, CHEN Tao

(State Key Laboratory of Materials Processing and Die & Mould Technology, Huazhong University of Science and Engineering, Wuhan 430074, China)

The dynamic recrystallization(DRX) behaviors of Cr12MoV steel were investigated by using Gleeble−3500 thermo-simulation machine at the deformation temperature varying from 1 050 ℃to 1 150 ℃, strain rate ranging from 0.01 s−1to 10 s−1. By using regression analysis result obtained from the investigation, a cellular automata(CA) model was built and used to simulate the DRX process of Cr12MoV. The results reveal that the hot deformation activation energy of Cr12MoV is 458.069 kJ/mol. As for the mean size of dynamic recrystallized grains, the relative error between the mean size simulated by CA and the experiment value is within 10.2%. Meanwhile, the predicted stress−strain curve obtained by CA can properly reflect the stress−strain curve features of the DRX. Corresponding well with experiment results, the relative error of peak stress between two curves is within 3.9%. It’s a positive correlation between the mean grain size and recrystallized percentage of DRX within a proper strain range. The higher the strain rate is, the more insufficient the DRX will be and it becomes easier to obtain smaller DRX grains with the increase of strain.

cellular automata; dynamic recrystallization; computational material science; microstructure simulation

TG142.33

A

10.11817/j.issn.1672-7207.2018.03.004

1672−7207(2018)03−0536−08

2017−03−19；

2017−05−12

教育部新世纪优秀人才支持计划项目(NCET-13-0229) (Project(NCET-13-0229) supported by the New Century Excellent Talents in University)

廖敦明，教授，博士生导师，从事铸造CAD/CAE、锻造有限元研究；E-mail: liaodunming@hust.edu.cn