基于有限元方法的轮胎滚动过程仿真分析

2018-04-11米伟姚银花

汽车实用技术 2018年6期

米伟，姚银花

（长安大学汽车学院，陕西西安 710064）

引言

轮胎是车辆与路面接触的最直接部件，轮胎性能的好坏直接影响到车辆的动力性、经济性以及行驶平顺性[1]。建立轮胎有限元模型，仿真分析车辆轮胎滚动过程。轮胎结构有限元模型的建立具有一定的难度，主要困难包括：（1）轮胎是有胎面、带束层、胎体、钢丝圈等构成的复杂架构；（2）轮胎运动过程中将会引起大的变形，而且轮胎的变形是非线性的；（3）轮胎橡胶材料的非线性。论文通过引入将 CAD模型转换为有限元模型的代码实现的 FE模型的灵活性使得能够进行研究，作为目标具有改进的轮胎性能，特别是其可操作性和加速度的改善[2]。

1　轮胎有限元模型建立

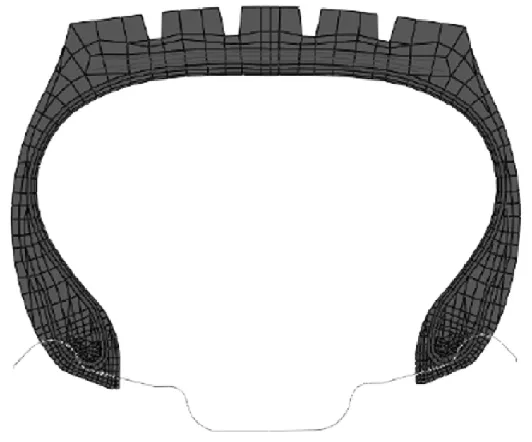
图1　轮胎二维有限元模型

本章描述的用于稳态滚动分析的 FE轮胎模型是根据作者开发的轮胎轮廓的2D参数CAD模型（如图1所示）创建的，该模型将在其他地方进行更详细的描述[3]。该模型基于早期开发的3D CAD模型，在轮胎胎面将被详细建模的情况下，可以容易地与其组合。新模型的优点是，除了轮胎轮廓的基本参数化几何外，还包含一个参数化的线和网络线，它们代表了FE网格的建模基础。

这里描述的 FE模型可用于所有轮廓类型，其轮廓以相同或类似的方式构造。如果要分析不同类型的轮胎，则需要通过重新制作新的CAD模型来创建新的CAD模型。轮胎的加速分析过程是通过编写将CAD模型中的点集合转换为FE模型的节点的代码来实现的[4]。以这种方式，每一种代码代表一种轮胎有限类型。在创建 CAD模型只需要改动节点位置，从而形成新的有限元模型。因此，可以在非常短的时间内产生大量不同的有限元模型，这样可以更有效地检查轮胎设计中参数变化对其滚动行为的影响[5]。

2　有限元结果分析

2.1　轮胎充气压力分析

轮胎结构部件中的应力分布也可用作滚动轮胎性能的一些方面的早期指标，如耐久性。轮胎充气变形形状如图2所示。

图2　充气压力为2bar，轮胎变形状况

轮胎侧壁上部及轮胎肩部附近已朝向轮胎的内侧偏转，而较靠近胎圈的下部已朝向外侧移动。这种趋势与根据滚动轮廓优化理论构造的轮胎的观察行为一致。根据该理论，选择胎体轮廓的几何形状，使其能够在滚动轮胎中气压均匀分布，从而减小滚动阻力。

图3　轮胎气压为2bar时，胎体帘布层受力分析图

通过图3我们可以发现当轮胎气压为2bar时，距离中心接触部位80-100mm处产生的应力最大，轮胎磨损也最严重的。

2.2　稳定滚态分析

稳态滚动分析的结果高度依赖于轮胎与地面之间摩擦的定义。橡胶摩擦是一个非常复杂的现象，其描述仍然是一个有吸引力的科学挑战。用于描述轮胎橡胶摩擦的常用方法之一是使用基于橡胶试样的实验室试验的现象模型。根据这种方法，接触对橡胶地面的摩擦系数表示为一个或多个变量的函数，通常是接触压力，滑动速度和/或温度。在论文中这些值从摩擦系数通过在沥青表面上的胎面橡胶试样的实验室测试获得。如表1所示。

表1　轮胎胎面胶料的摩擦系数值

2.3　自由滚动转弯分析

为了评估轮胎的可操作性，进行转弯分析后进行加速分析。在这种实验方案下已经包括了自由转弯滚动分析。在这种分析中，在直线自由滚动的平衡状态建立后，滑移角逐渐变化，直到达到预定值。

根据SAE约定的滑移符号如图4所示。当滑移角为正时，作用在轮胎上的侧向力为负。

图4　SAE坐标系中在左转（正滑角）的有限元轮胎模型

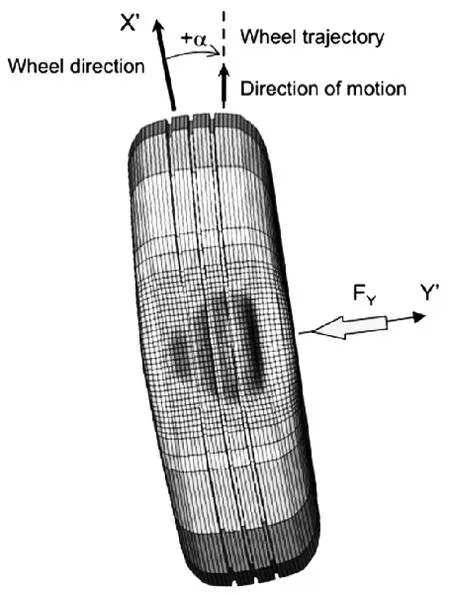
图5　FE轮胎模型左转中的变形形状和的接触压力分布

图5展示出了左转中的转弯轮胎的接地印迹形状和接触应力分布，轮胎以80km/h和滑动角8°滚动，通过轮胎的接地应力状态可以看出，位于转弯外侧的接触印迹中右侧的接触压力较高。

在其它的文献中，转弯分析的结果表现为滑移角与侧向力或滑移角与自动回正力矩的相关性。图6为对于具有可变摩擦系数的有限元轮胎模型在以速度为80km/ h进行自由转弯时获得的滑移角和侧向力之间的相关性。根据SAE坐标系的滑移角值为正的图形右侧对应于左转，而左侧对应于右转。

图6　滑移角和侧向力之间的相关性

从上图滑移角和侧向力关系曲线可以看出。轮胎模型在滑移角度为7°至8°之间时，轮胎的摩擦力达到最大值。

对于轮胎在给定的80km / h滚动时，驾驶员作用在方向盘上感觉到的阻力来自于车轮自动回正时产生的力矩，自动回正力矩的大小随随滑移角变化关系曲线如图7所示。

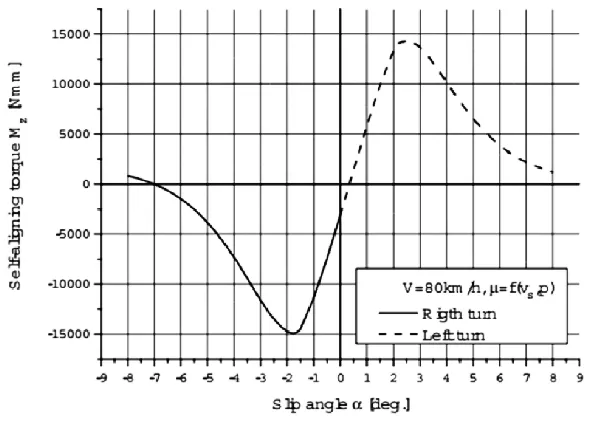
图7　自动回正力矩和滑移角之间的相关性

通过仿真获取的曲线我们可以得知，在大约滑移角+2.2°和-1°之间时，自动回正力矩达到极值。随着滑移角绝对值不断变大，自动回正力矩的绝对值开始下降。在右转的情况下，对于滑移角大于 7°的值，甚至改变了方向，这让驾驶员感觉自己仿佛在冰面上行驶。

上图对于可变摩擦系数的轮胎模型以 80km/h滚动的获取的自动回正力矩和滑移角之间的相关性可以看出，对于零滑移角，侧向力和自动回正力矩也不等于零。这是轮胎带束层相对于车轮平面反对称的结果。当这些不为零的力和力矩在作用在同一轴上的一对轮胎上使其产生不平衡，这就是为什么车辆发生偏转而不是直线运动，即偏向一侧。