基于熵权法的集对分析模型在配电站项目后评价中的应用

吴　昊，安　帅，柴　俊，周　琰

(国网上海市电力公司市北供电公司，上海　200072)

随着社会经济的发展，配电站项目与日俱增。这些配电站投入使用之后是否能达到预期的效果，从项目后评价角度来看是否符合要求，能否从项目后评价结果之中吸取经验教训使后续建造的配电站更加具有竞争力是项目管理人员必须关注的一个问题。

配电站后评价一直以来没有一个非常合适的方法，原因是影响配电站项目的参数众多，从不同的角度去评价各个参数的权重大不相同。在其他学科中也有类似的问题，特别是水环境和煤矿安全性评估[1-2]，指标错综复杂。

熵权法[3-4]针对类似的问题有其特有的优势，它从各个参数本身数据出发，关注不同评价对象中同一参数大小的差别，同一参数差别大的认为权重高，差别小的认为权重低，这一特点能为配电站评价提供极大地便利。同时，集对分析是一种能够处理不确定关系及考虑边界的模糊性评价方法，并且在综合评价中得到一致好评。本文将熵权法的集对分析模型(以下简称熵权集对模型)[5-6]引入配电站项目后评价，以寻求配电站项目后评价可行可靠的方法。

1　基于熵权法的集对分析模型

1.1　熵权法确定权重

根据配电站项目参数的特点，用熵权法确定各指标的权重，其具体计算步骤如下[7]。

(1)设有m个评价对象，每个对象有n个评价指标，基于最大隶属度原则，将指标数值标准化处理，消除量纲对评价结果的影响。对于越大越优型和越小越优型指标的标准化处理方法分别为

(1)

(2)

式中rjk——第j个评价对象的第k个评价指标的标准化值；Xjk——第j个评价对象的第k个评价指标特征值；Xmax、Xmin——第k个指标的最大值和最小值。

从而得到决策矩阵：R=(rjk)m×n。

(2)第k个评价指标熵的定义为

(3)

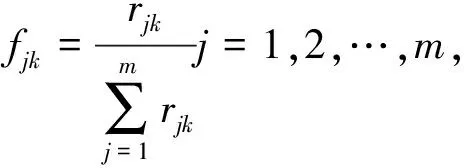
(3)第k个指标的权重为

(4)

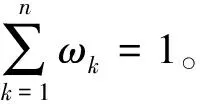
1.2　集对分析法分析评价

集对分析从同、异、反三个方面研究两个事物的确定性与不确定性，能全面刻画两个不同事物的联系，对两个事物对比中的模糊部分有比较好的描述[8]。按照集对的某一特性展开分析，对集对在该特性上的联系进行分类定量刻划，得到集对在某一问题背景下的联系度式：

u=a+bi+cj

(5)

式中a——两个集合的同一程度，称为同一度；b——两个集合的差异不确定程度，也称为差异度；c——两个集合的对立程度，称为对立度。根据定义，a，b，c满足归一化条件a+b+c=1。

集对分析法流程图见图1。

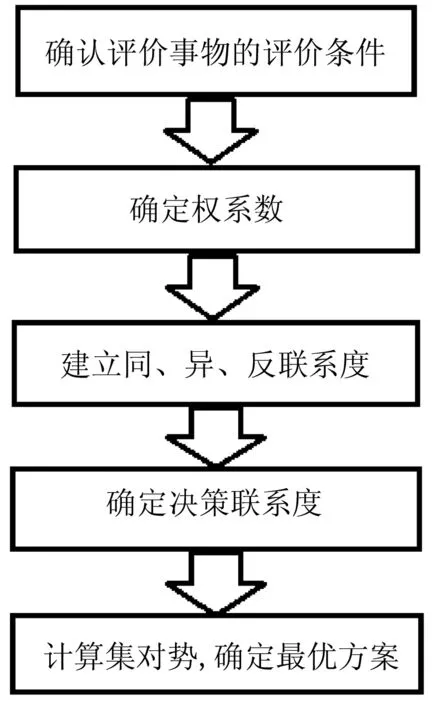
图1　集对分析法流程图

对于集对分析来说，除了确定权系数其他步骤都是可操作的，如果与熵权法结合，能对模糊不确定的事物进行有效地评价比较。

2　算例验证及其分析

2.1　案例简介及指标体系的构建

某市根据规划建造了许多大小规模相近的小区，电力部门为了便于管理对其中已建好居民已入住的四个小区的供电性能指标进行一次评价，以确定哪个小区的配电站供电性能指标比较好，可以作为试点，将其经验供其他小区学习。

根据电力系统中的重要参数，评价时选取指标要根据电力系统的实际情况。利用了选取指标体系的综合法并根据选取指标体系的原则建立的指标体系[9]。该地区配电网评价指标的结构图见图2。

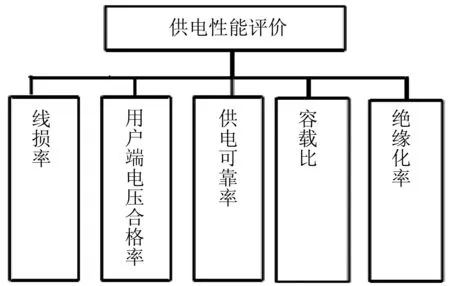
图2　评价指标结构图

经过处理，这些指标汇总到一张表中数据见表1。

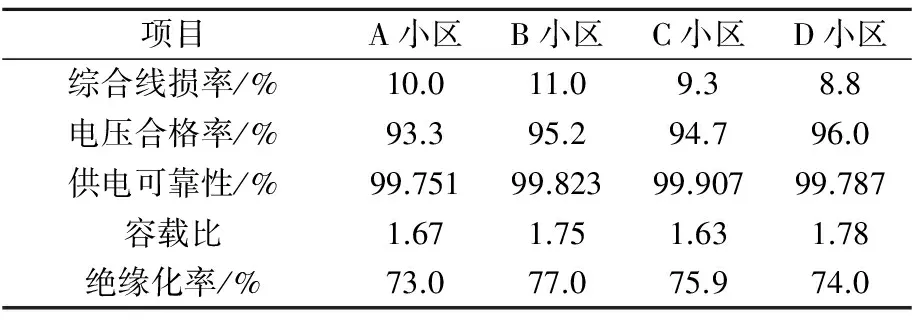
表1　配电站评价指标汇总表

2.2　利用熵权集对分析法项目后评价

(1)熵权法确定权系数。由式(1)和式(2)得：

由式(3)得：

进而得到：

Hk=[0.7580.7670.6760.7090.703]

因此，可以得到权系数向量：

ω=(0.174,0.168,0.234,0.210,0.214)

(2)集对分析法分析。对于项目希望越大越好的指标的a和c联系度公式为

(6)

(7)

对于希望越小越好的指标a,c联系度为

(8)

(9)

b=1-a-c

其中，Mij为第j项目的第i个指标，Mi max为第i个指标的最大值，Mi min为第i个指标的最小值。利用式(6)、式(7)、式(8)、式(9)建立4个配电站各个指标同、异、反联系度通过与熵权法得出的权重加权，结果如下：

uA=0.492+0.002i+0.506j
uB=0.496+0.001i+0.503j
uC=0.501+0.001i+0.498j
uD=0.514+0.001i+0.485j

由集对势公式shi(Hh)=ah/ch分别得出A、B、C、D四个项目的的集对势分别为

由熵权集对分析法最终得出的A、B、C、D这4个小区的供电性能优劣排序为D、C、B、A。

2.3　利用TOPSIS法和功效评分法验证结果的正确性

2.3.1TOPSIS法

由TOPSIS法的理论构建矩阵：

无量纲化得：

进行加权，TOPSIS法一般用离差权法得到权重，加权向量为

ω=(0.56,0.09,0.01,0.21,0.13)

uij=ωjzij

(10)

加权后从uij中得到：

u+=(-0.252 0,0.045 9,0.005 0,0.109 2,0.066 0)T

u-=(-0.313 6,0.044 1,0.005 0,0.100 8,0.063 0)T

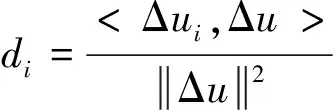
dA=0.024,dB=0.000 85,dC=0.042,dB=0.052

可见，通过TOPSIS法最终得出的A、B、C、D这4小区的供电性能优劣排序为D、C、A、B。

2.3.2功效评分法

功效系数计算结果见表2。

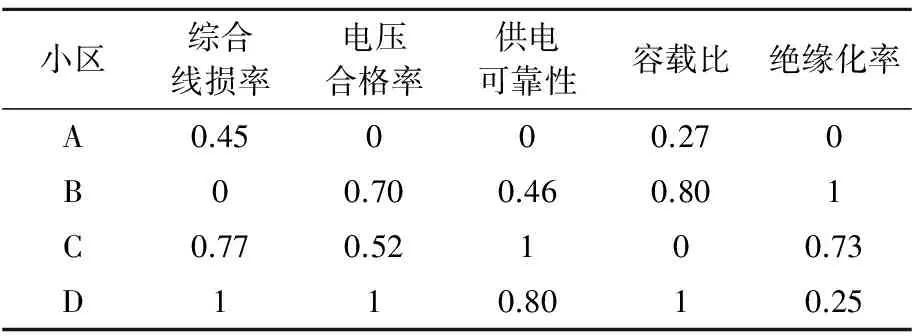
表2　功效评分法计算结果

利用均权加权，得：

uA=0.144uB=0.592

uC=0.604uD=0.696

因此，通过功效评分法最终得出的A、B、C、D这4个小区的供电性能优劣排序为D、C、B、A。

各种方法的结果汇总见表3。

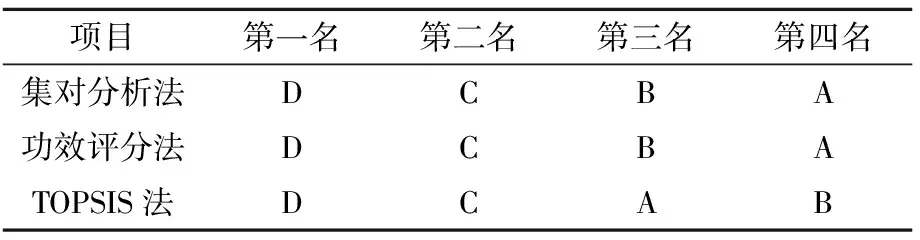
表3　三种方法结果汇总

由表4可以看出，熵权集对分析法和功效评分法得到的结果相同，结合TOPSIS法的结论分析，A和B小区配电站的优劣存在争议。这可能是因为每种计算方法看待问题的角度不同，可能造成结果的偏差，也有可能是不同的权重体系造成了有差异的结果。但是最优配电站项目D在三种评估方法中毫无争议，这也是对这个案例计算的目的，因此计算结果是理想的，验证了熵权集对分析法在配电站项目后评价中是适用的。同时，用熵权法确定指标的权重有很强的可操作性，并且有很强的说服力，差异大的指标权重大这个特点能让评价者更清楚地看到项目之间的差异，从差异出发，寻找弱点，为后续项目的改进提供依据。

3　结语

本文引入熵权集对分析模型对配电站项目进行后评价，结合算例进行计算和分析，同时经过与经典方法的对比，取得了比较满意的结果。

(1) 建立了完整的熵权集对分析法配电站项目后评价的思路流程以及计算方法。

(2) 虽然TOPSIS法的计算结论与另外两种有所不同，但在最优配电站选取上三种方法是一致的。计算过程中熵权集对模型的优势是明显的，熵权法确定权重时从指标数据出发，突出指标的差异性，集对分析比较时从同、异、反三方面描述评价对象，得到的结论更加可靠。

参考文献：

[1]贡力,余涛.集对分析法在水安全评价中的应用[J].中国农村水利水电,2015(1):58-62,67.

GONG Li, YU Tao. The application of set pair analysis method in water security evaluation[J].China Rural Water and Hydropower, 2015(1): 58-62,67.

[2]徐宏杰,宫博,李德顺.基于集对分析法的煤矿危险性评价[J].中国安全生产科学技术,2012,8(6):86-90.

XU Hongjie, GONG Bo, LI Deshun. Risk assessment of coal mine based on set pair analysis[J].Journal of Safety Science and Technology, 2012, 8(6): 86-90.

[3]孟宪萌,胡和平.基于熵权的集对分析模型在水质综合评价中的应用[J].水利学报,2009,40(3): 257-262.

MENG Xianmeng, HU Heping. Application of set pair analysis model based on entropy weight to comprehensive evaluation of water quality[J].Journal of Hydraulic Engineering, 2009, 40(3): 257-262.

[4]谢正文,吴超,李孜军,等.基于信息熵和集对分析理论的硫化矿石自燃倾向性判定[J].中南大学学报(自然科学版),2012,43(5):1858-1863.

XIE Zhengwen, WU Chao, LI Zijun, et al. Evaluation on spontaneous combustion tendency of sulfide ores based on entropy and set pair analysis theory[J].Journal of Central South University, 2012, 43(5): 1858-1863.

[5]王光平,卢宗华,王斌贝,等.同异反联系度在决策方案评价与优选中的应用[J].山东矿业学院学报(自然科学版),1999(4):121-123.

[6]刘俊华,罗隆福,张志文,等.基于模糊集对分析法的电能质量综合评估[J].电网技术,2012,36(7):81-85.

[7]马冬梅,陈大春.基于熵权法的模糊集对分析模型在乌鲁木齐市水资源脆弱性评价中的应用[J].水电能源科学,2015,33(9):36-40.

[8]赵克勤.集对分析及其初步应用[M].杭州:浙江科学技术出版社,2000.

[9]杜栋,庞庆华.现代综合评价方法与案例精选[M].北京:清华大学出版社,2005:1-207.