面向长模式串的改进型AC算法研究

◆岳小伟 詹 瞻



面向长模式串的改进型AC算法研究

◆岳小伟 詹 瞻

（信息工程大学 河南 450001）

在面向实时数据流的分类研究中，基于AC算法的多模匹配已具备一定的应用基础。本文针对数据流中的长模式串特征，提出了AC_TE算法的改进算法——AC_LSE算法，适用于高速实时网络数据流的识别分类。该算法利用1个Hash表存储当前匹配窗口对应的不同前缀字符串的跳转距离，需要进行跳转时，直接查找Hash表进行跳转，减少了字符比较和查找开销，提高了多模匹配的效率。实验结果表明，该算法在多模匹配的速度和比较次数上，均优于AC_TE算法，在长模式串的匹配上性能更佳。

数据流分类；AC_LSE算法；跳转距离；Hash表

0 引言

模式匹配时是指在目标序列中查找模式串的过程，若找到则匹配成功，否则匹配失败，即失配。随着互联网技术的发展，网络数据呈现出爆炸性增长的态势，如何有效地将这些数据进行分类和解析，已成为当前互联网技术发展亟需解决的问题。在实时数据流分类应用中，多模匹配已成为一种关键技术，特别是针对高速数据流实时处理，在已掌握大量应用数据特征的前提下，处理效率是考察系统的重要指标，直接影响分类器的性能。

在已有的研究中，文献[1]中的KMP算法是由是由Knuth等人提出的一种单模匹配算法，对于任何模式和目标序列，均在线性时间内完成匹配查找，算法的时间复杂度为O(n + m)；文献[2]中的BM算法是由Boyer和Moore提出的一种基于后缀匹配的单模匹配算法，为了使模式串高效的移动，算法定义了两个规则：坏字符规则和好后缀规则，根据两者的较大值来确定跳转距离；1975年贝尔实验室的Aho和Corasick提出了AC算法[3]，该算法基于不确定的有限自动机，对于长度为n的目标序列，算法能在线性时间复杂度内，找到文本中的所有模式，与模式集规模无关；文献[4]中Coit、Staniford 和McAlerney将AC算法的自动状态机和BM算法的启发式跳跃策略相结合，提出了AC_BM算法，利用两者的优点，效率同时优于AC算法和BM算法；文献[6]的AC_BHM算法和文献[7]的AC_QSS算法，均在AC算法的基础上进行改进，但模式树的最大移动距离仍为最短模式串长度，没有提高最大移动距离；文献[8]将AC算法和SUNDAY算法相结合提出的AC_SUNDAY算法，使模式树的最大移动距离达到minlen+1，最大移动距离增加不明显。文献[5]中的AC_TE算法根据当前匹配窗口的前3个字符，生成1个字符串跳跃表和2个哈希表来确定移动距离，使模式树的最大移动距离增加为最短模式串长度加3。与AC算法相比，AC_TE算法在匹配速度上有了极大的提升，但算法的预处理步骤复杂，在匹配过程中会增加不必要字符的比较和哈希查找开销，而针对实时数据流进行分类，需要较高的处理速度，否则极易出现丢包现象，影响分类结果的准确性。本文从减少AC_TE算法字符比较和减少哈希查找开销的角度，提出了一种用空间开销换取处理效率的AC_LSE（LONG STRING EFFICIENT）算法。

1 AC_TE算法

AC_TE算法是在AC算法的基础上，根据当前匹配窗口的前3个字符，设计出一种新的模式树移动规则，在预处理阶段生成1个字符串跳跃表和2个哈希表，用于辅助计算模式树的移动距离。匹配阶段则根据这3个字符在不同条件下，比较和查找对应的哈希表，然后计算出模式树的移动距离。该算法的主要思想是利用当前匹配窗口前缀的不同，在扫描过程中尽可能跳过更多字符，即增加模式树的移动距离，提高了匹配速度。

1.1预处理阶段

（1）构建模式树

从模式树的根节点开始，遍历所有的模式串，将模式串的每一个字符，放到模式树上成为一个节点。每个字符的前一字符所对应的节点，都为该字符对应节点的父节点。如果该字符对应的节点已经存在，则不再添加新的节点。记录每个模式串的最后一个字符对应节点为结束节点，当匹配成功时，进行输出。以模式集P={hers，his，here}为例，构建的模式树如图1所示。

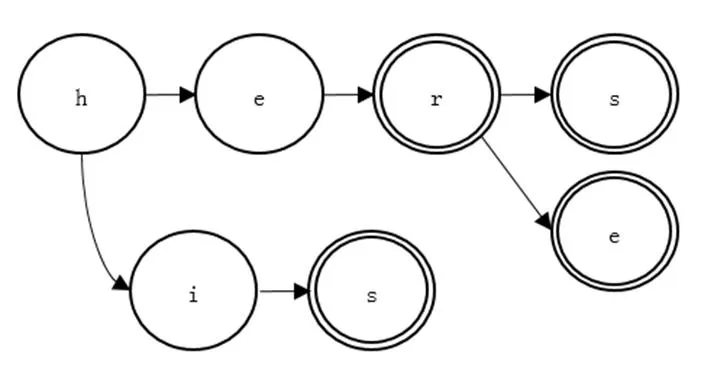
图1 模式树

（2）创建SST表（字符串跳跃表）

SST表记录了minlen深度内两两相邻字符组成的字符串到模式树根节点的距离，记为depth(S)，其中S=Pi[m]Pi[m+1]，1≤i≤r，1≤m≤minlen-1，则depth(S)=m-1，如果S出现多次，则取最小值。在模式集P={hers，his，here}中，最短模式为his，长度为3，则SST表包含{he，er，hi，is}，depth(he)=depth(hi)=0，depth(er)=depth(is)=1。

（3）创建LTST表（末层字符串哈希表）和LCT表（末层字符哈希表）

设当前模式集中最短模式串长度为minlen，LTST表中记录了每个模式串中第minlen-1和minlen层字符组成的字符串；LCT表则记录了第minlen层字符。在模式集P={hers，his，here}中，LTST和LCT表项分别为{er，is}、{r，s}。

1.2匹配过程

初始时，将模式树中最短模式串右端与目标序列末端字符对齐，从模式树的根节点开始，按照从左向右的顺序进行匹配。利用goto函数进行状态转移，当匹配成功时则输出匹配成功的模式串。发生失配时，计算移动距离shift length，并将模式树左移shift length位。重复此过程，直到模式树与文本串的首字符对齐，匹配过程结束。计算移动距离shift length伪代码如下：

输入 SST，LTST，LCT，x，y，z，minlen，其中x,y,z分别表示当前匹配窗口的前3、前2和前1字符

输出 模式树移动距离 shift length

if(z==首字符)

shift length=1；

else if(yz∈SST表)

shift length=depth(yz)+2；

else if(hash(xy)->LIST==true)

shift length=minlen+1；

else if(hash(x)->LCT==true)

shift length=minlen+2；

else

shift length=minlen+3；

返回 shift length

2 AC_LSE算法描述

随着高性能计算机的广泛运用，廉价的硬件资源可以用于换取处理效率， AC_TE算法中运用多张表来计算模式树移动距离，实现了模式树的最大移动由最短模式串长度增加到最短模式串长度加3，但算法的预处理步骤复杂，在匹配过中会增加不必要字符的比较和哈希查找开销。在此基础上，本文针对AC_TE算法进行改进，在不影响算法时间复杂度和不产生漏检的前提下，设计出更高效的AC_LSE算法，以内存开销换取匹配速度，减少不必要字符的比较和查找开销，以适应实时数据流分类的需要。改进思想如下：

设当前匹配窗口的前3个字符分别为x，y，z，模式集中最短模式串长度为minlen，生成的哈希表空间大小为256*256*256*2字节（有实验数据表明，当哈希表负载不超过50%时，性能较高），AC_LSE算法生成哈希跳转表规则如下：

（1） 初始化设置所有的Hash表空间的值为最短模式串长度加3，即hash[*,*,*] = minlen+3，其中*表示任意ASCII表字符；

（2） 对于任一模式串，如果x与模式串第minlen层字符相同，则移动距离为minlen+2，即hash[x,*,*] = minlen+2；

（3） 如果xy组成的字符串与任一模式串第minlen-1和第minlen层字符组成的字符串相同，则移动距离为minlen+1，即hash[x,y,*] = minlen+1；

（4） 如果yz组成的字符串在模式树minlen深度内出现，则选取到模式树首层字符距离最短的出现位置，记为depth(yz)，则移动距离为depth(yz)+2，即hash[*,y,z]=depth(yz)+2；

（5） 如果z为模式树首层字符，则移动距离为1，即hash[*,*,z]=1。

生成Hash跳转表的伪代码如下，

输入 P={P1, P2,…，Pr},最短模式串长度minlen，depth(Pi[m]Pi[m+1])，其中1≤i≤r，1≤m≤minlen-1

输出 Hash跳转表

//算法步骤1

初始化置hash[*,*,*]= minlen+3;

for(i = 1;i <= r;i++) //处理模式集中的每一个模式串

{ //算法步骤2

for(j = 0;j < 256;j++) {

for(k = 0;k < 256;k++) {

hash[Pi[minlen],ch(j),ch(k)]=minlen+2;

hash[ch[j],ch[k],Pi[0]] = 1;

} }

//算法步骤3

for(k = 1;k < 256;k++) {

hash[Pi[minlen-1],Pi[minlen],ch(k)]=minlen+1;

}

//算法步骤4

for(k = 1;k < 256;k++) {

for(m=1;m <= minlen-1;m++) {

hash[ch(k),Pi[m],Pi[m+1]]=depth(Pi[m]Pi[m+1])+2;

} }

//算法步骤5

for(j = 0;j < 256;j++) {

for(k = 0;k < 256;k++) {

hash[ch[j],ch[k],Pi[0]] = 1;

} } }

返回Hash跳转表

以模式集P={abc，aef，aaaef}为例，最小的模式串长度为3，SST表项为{ab，bc，ae，ef，aa}，其中SST(ab)=SST(ae)=SST(aa)=0，SST(bc)=SST(ef)=1。设当前目标序列T=abcgaaefjkp，则匹配过程如图2所示，初始时将最短模式串最右字符与T的末端字符对齐，发生失配。此时xyz=aef，根据规则4，ef串aef和aaaef的子串，hash[*,y,z]=ef最小深度+2=1+2=3，模式树左移3位，第一次移动后匹配出aef。移动后xyz=cga，z=a为模式串首字符，此时根据规则5，模式树左移1位。比较过程中发生失配，此时xyz=bcg，根据规则3，hash[b,c,*]=minlen+1=3+1=4，第三次移动后匹配出abc。

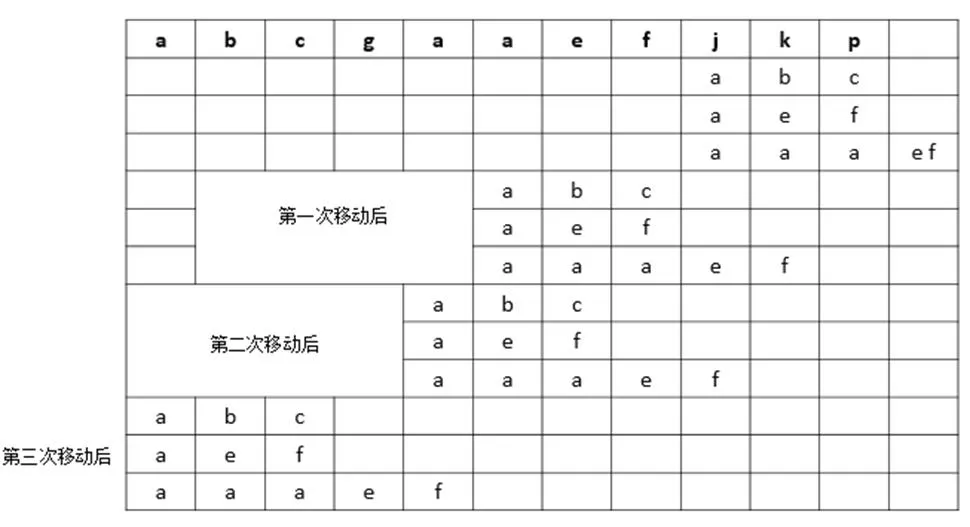
图2 AC_LSE算法匹配过程

由此可以看出在每一次跳转时，只需根据当前匹配窗口的前3位字符组成的字符串，结合预处理时生成的哈希表进行跳转，而AC_TE算法的匹配过程则需要根据不同的xyz值进行查找比较后再计算出跳转距离，增加了字符比较和Hash查找开销。AC_LSE算法通过统一的Hash映射，实现了跳转长度的快速查询，减少了不必要字符的比较，提高了匹配效率。

3 实验结果

测试环境为Intel(R) Xeon(R) CPU E7-4820 v2 @ 2.00GHz，8核，内存256G的Linux X64服务器。测试数据为从kdd.ics.uci.edu选取英文新闻文本作为匹配输入，大小为37M，并从文本的随机位置生成了长度为4字节、8字节、16字节、32字节的模式串各500个，从算法的执行时间和比较次数上与AC_TE算法进行对比，测试结果如图3、图4所示。

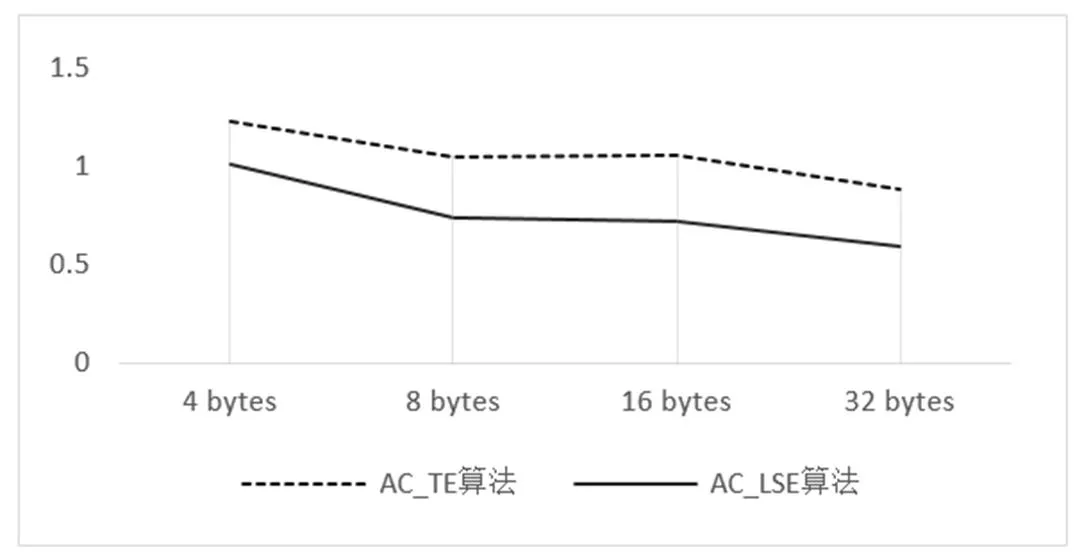
图3 不同长度模式串匹配耗时对比图

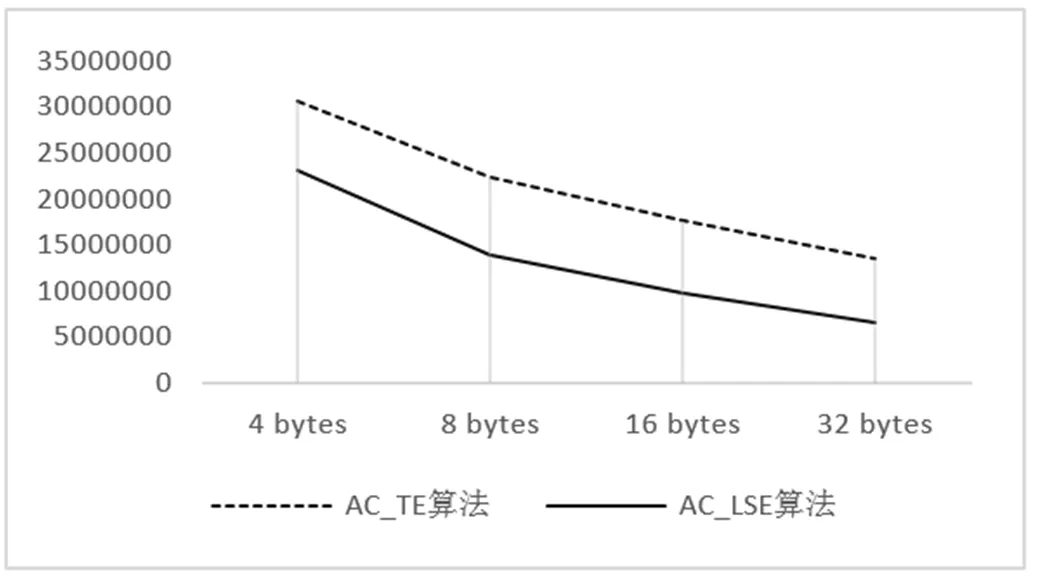
图4 不同长度模式串比较次数对比图

图3和图4的横坐标表示模式串长度，纵坐标分表表示算法执行时间和比较次数，执行时间单位为秒（s），每种长度的模式串个数均为500个。由图3可知，改进后的算法的时间开销优于AC_TE算法，且随着模式串长度越长，匹配耗时越短。这是因为随着模式串长度的增加，失配的概率也随之增大，从而间接增加了模式树以最大距离移动的概率。图4则表明改进后算法在比较次数上明显减少。同时，将2000个不同长度的模式串进行匹配验证，AC_TE算法耗时3.44秒，AC_LSE算法耗时2.90秒。由实验结果不难得出，AC_LSE算法在匹配速度和比较次数上，均优于AC_TE算法。

4 结语

本文针对AC_TE算法进行优化，以空间开销换取匹配速度的方式，将AC_TE算法的多张规则表统一映射到一个统一的Hash空间，减少了比较和查找开销。通过实验验证了改进算法的效率。实验结果表明，改进后的AC_LSE算法在执行时间和比较次数上均优于AC_TE算法。在数据流分类应用中，不同应用对应数据包特征长度都会偏长，这与AC_LSE算法相一致，该算法在数据流分类中的应用将是本文的后续课题。

[1]Knuth DE,Morris JH,Pratt VR. Fast pattern matching in strings[J]. SIAM J Comput，1977.

[2]Boyer RS,Moore JS. A fast string searching algorithm[J]. Communications of the ACM，1977.

[3]Aho A V,Corasick M J. Efficient string matching: an aid to bibliographic search[J]. Communications of ACM，1975.

[4]Coit C J,Staniford S. Toward Faster String Matching for Intrusion Detection or Exceeding the Speed of Snort[C]. Proc. of the DISCEX，2001.

[5]刘春晖，黄宇，宋琦.一种改进的ＡＣ多模式匹配算法[J].计算机工程，2015.

[6]刘升，陈志刚，邝祝芳.认知无线电中结合差异性的免疫克隆优化频谱分配算法[J].计算机工程与科学，2014.

[7]El-Nainay,Mustafa Y.Island Genetic Algorithm-based Congnitive Networks[D]. Blacksburg,USA: Virginia Polytechnic Institute and State University,2009.

[8]赵知劲.基于量子遗传算法的认知无线电频谱分配[J].物理学报, 2009.