基于Kullback-Leibler距离的循环经济园区网络重要节点识别方法

毛泽天

（北京信息科技大学经济管理学院， 北京　100192）

引言

随着经济社会迅速发展，无限的资源需求与有限的资源储备间的矛盾日益加剧。在这一大背景下，循环经济的概念逐渐兴起。循环经济园区是循环经济的重要载体，对影响园区运行稳定性的因素进行分析无疑将提升园区的可持续性及可复制性，为我国继续走新型工业化道路提供理论支持[1]。目前对于循环经济园区评价体系的研究多集中在物质流、减量化等方面，对于园区拓扑结构进行系统性评价的研究还比较少，而复杂网络恰好适用于此。现有研究结果显示在现实网络中，不同节点的地位并不相同，对网络拓扑结构及功能的影响也存在显著差异。因此，在循环经济园区网络中挖掘出重要性较强的节点，对指导实际工作具有重要意义。

1　节点重要度排序研究现状

节点重要度排序是重要节点识别的主要研究内容，近年来受到国内外广泛关注，也提出了各种节点重要度排序方法，主要有：度中心性、K-shell分解方法、ClusterRank算法接近中心性、介数中心性、连通介数中心性、特征向量中心性、节点删除的最短距离法等。除上述几类定量分析方法，还有一些基于某几个指标或节点属性进行排序的综合分析方法，如层次分析法、综合加权法、Kullback-Leibler距离法[2]等。通过分析可知，各种单一分析方法通常各有优缺点，难以全面评价园区网络的情况。

2　基于Kullback-Leibler距离的综合节点重要度评价

为全面考虑节点的各种特性，综合评价其重要程度，本文从节点的局部特性、全局特性、传播特性和在网络中的位置四个角度分别选取度中心性、接近中心性、介数中心性、K-shell分解方法[3]作为其基本指标，并将原本只能应用于无向网络的K-shell方法推导到有向网络，最后基于Kullback-Leibler[4]方法，根据这四个基本指标的评价结果，通过结果间一致性偏差最小化的约束，得到循环经济园区有向网络节点重要度的评价方法。

2.1　改进的K-shell分解

K-shell分解算法直接应用于循环经济园区有向网络将会面对以下几点问题。

1）不能直接给出有向网络中节点的k-shell值。

2）需假设网络中不存在度为0的节点，与园区网络实际情况不符。

3）分解结果的层次性较差，不能较好地区分不同节点重要度的差异。

基于以上几点问题，现提出改进的有向网络k-shell分解方法：分别计算节点的入K-shell值和出K-shell值。

首先，去掉网络中入度最低的节点，由于是有向网络，很可能存在入度k=0的节点，则去掉网络中入度k=0的所有节点，将这一步中去掉的所有节点记为网络的入1-shell（入1-壳）；重复上一步，去掉网络中入度最低的节点，将在这一步中去掉的节点记为网络的入2-shell。不断重复以上步骤，得到网络的入3-shell、入4-shell以及更高的shell层，直到网络中的所有节点均被去掉，此时网络中所有节点都有其对应的入K-shell值ks入。

同理，可以得到网络中各节点的出K-shell值ks出。

在循环经济园区中，每个节点项目无论是对其紧后还是紧前节点均有重要的影响，因此将入K-shell值和出K-shell值视为同等重要，因此有

2.2　基于Kullback-Leibler距离的综合节点重要度评价

K-L距离[4]又叫做相对信息熵，它的定义是：设有两个密度函数f（x）和g（x），他们的支撑集分别为Sf和Sg。若Sf⊆Sg且，则称KL为f（x）到g（x）的K-L距离。

根据定义，设节点vi的四项基本指标构成的评价向量为Pi=[pi1,pi2,pi3,pi4]=[DCi,CCi,BCi,IKsi]，根据各项指标的定义可知，节点在各项指标上的得分越高，则其在网络中的重要度越高。由于各基本指标的量纲不尽相同，为了便于后续分析，定义节点vi的重要度评价向量为Ri=[ri1,ri2,ri3,ri4]，其中在本文中，i∈{1,2,…,n},j=1,2,…,l,l=4。

现在假设存在一个重要度最高的虚拟节点v*，其重要度评价向量为和一个重要度最低的虚拟节点v-，重要度评价向量为其中，r*j是所有网络节点在第j个指标上的最优值，r-j是所有网络节点在第j个指标上的最差值。

将虚拟节点v*和v-作为基准，基于K-L距离，给出网络节点vi到虚拟节点v*和v-之间的差异度量公式：

在应用实际网络进行计算的过程中，直接应用上述方法可能出现rij=0的情况，计算将无法继续。为解决这一问题，在不影响最终排序结果的前提下对定义进行改进。

其中，αj是一个很小的正数，取值方法为max{pij}的数量级乘以0.01。

根据网络节点vi分别到虚拟节点v*和v-之间的K-L距离，可计算节点vi以这两个虚拟节点为基准的重要度综合评价取值：

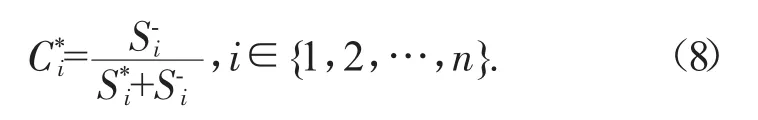
3　网络节点重要度的一致性排序

将四项基本指标（DC，CC，BC，IKs）分别作为评价指标对网络节点进行排序，可得到四组节点重要度的排序结果（RkDC,RkCC,RkBC,RkIKs）。由于不同的指标各有侧重，所以简单将四种方法按照相同的贡献度进行综合的排序结果存在相当的片面性和局限性。考虑到不同网络之间拓扑结构的差异性，应该对网络节点各指标的贡献度进行一致性排序。

设各指标权重向量W=[w1,w2,w3,w4]，Rwi=[w1ri1,w2ri2,w3ri3,w4ri4]，将给定权重之后的重要度综合排序结果记为RkKLw。各指标的权重以及节点的一致性排序即可根据以下两个约束条件进行规划求解得出。

其中，

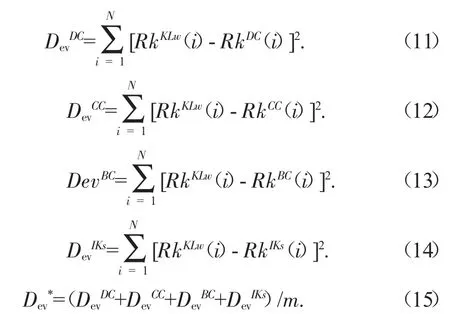
以上约束规划中，首先以式（9）为优化目标，可得到各项指标权重的可行域，再以式（10）为优化目标，可以确定最优化的权重取值，同时得到网络节点重要度的一致性排序结果。其中，式（9）的含义为极小化节点各节点各相应指标一致性偏差的总和，使综合排序结果与四组基本排序结果的偏离程度最小；式（10）的含义为极小化各节点各相应指标一致性偏差的方差，使综合排序结果与四组基本指标排序结果的偏离程度最均衡；式（11）（12）（13）和（14）分别是网络节点综合排序结果与四组基本指标排序结果的偏差；式（15）是综合排序结果与四组基本指标排序结果的偏差的平均值。

4　实例计算与分析

以江苏省某循环经济园区为例，应用本文方法进行节点重要度排序并对排序结果进行分析。

对该循环经济园区进行复杂网络建模，并进行节点编号，如图1所示。

图1　江苏省某循环经济园区有向网络模型

经过计算，得到该循环经济园区网络中各节点的指标特征值pij、评价值rij、综合评价值C*i及其在各种指标下的排名，其中排名前5的节点如表1所示。

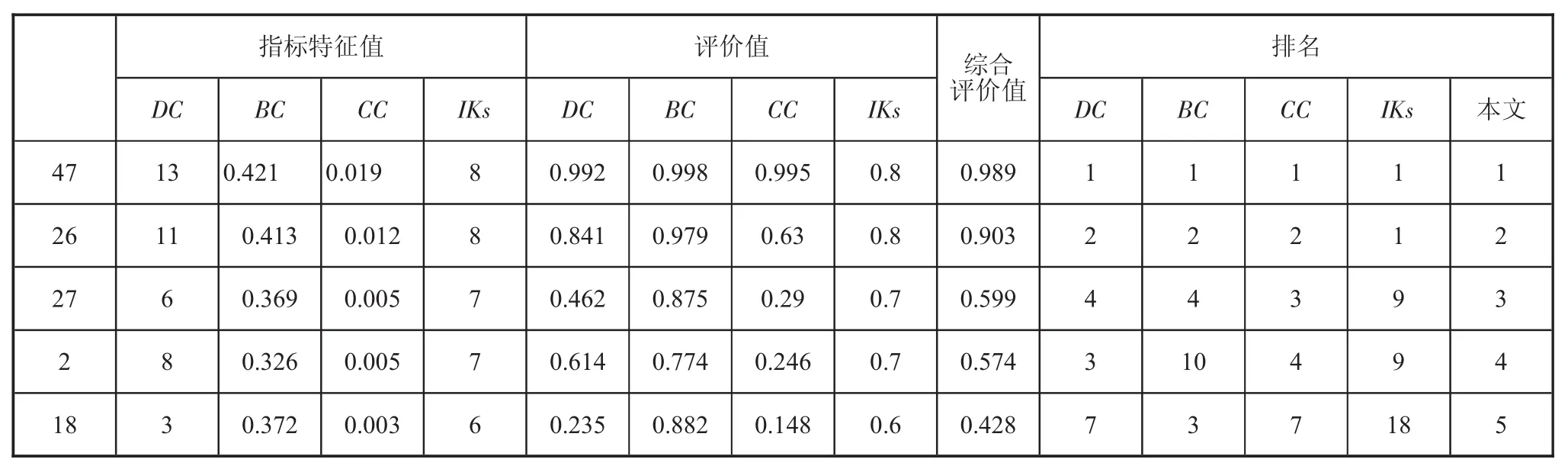
表1　江苏省某循环经济园区网络节点一致性排序结果

在本方法求解过程中，得到各指标的权重为[wDC,wCC,wBC,wIKs]=[0.09,0.22,0.09,0.6]。由此可知，在本网络中，节点各指标的重要性顺序为：网络位置＞全局属性＞局部属性=传播属性。

通过本文方法得出的园区网络节点重要度排序结构中，名次重复的节点共有10个，相对应，度中心性的排序结果中有43个名次重复的节点，介数中心性有18个，接近中心性有41个，K-shell值有47个。本方法得出的排序结果在合理范围内，且对园区各节点的重要程度有更清晰的划分，具有更强的实践指导意义。

5　结论与展望

对循环经济园区进行复杂网络建模并进行节点重要度排序对于提升园区运行的鲁棒性具有重要意义。为了保证园区节点重要度排序结果的有效性和实用性，本文主要做了以下工作：一是提出了循环经济园区的有向无权复杂网络建模方法；二是将K-shell方法方法推导到有向网络；三是引入K-L距离方法对节点重要度进行综合评价；四是根据网络自身结构特性建立一个约束条件，最终得到循环经济园区网络的节点重要度排序。最终案例分析结果表明该方法能够准确、有效地评价循环经济园区节点的重要性。

[1]白洮.循环经济下影响静脉产业园区稳定性的因素研究[J].生产力研究，2010，219（10）：226-227.

[2]刘忠华，王菊韵，郭晓玲，等.基于Kullback-Leibler距离的网络节点一致性排序[J].系统工程理论与实践，2016，36（8）：2 127-2 134.

[3]Kitsak M,Gallos L K,Havlin S,et al.Identification of influential spreaders in complex networks[J].Nature Physics,2010,6（11）：888-893.

[4]蔡择林，李开灿.常见分布的最大Kullback-Leibler距离[J].武汉大学学报（理学版），2007，53（5）：513-517.