微细铝丝辊式连续矫直工艺参数的优化*
2018-04-10郭勇,曹岩,方舟
郭 勇,曹 岩,方 舟
(西安工业大学 机电工程学院,西安 710021)
随着生产发展的要求,许多新型的矫直机被人们开发使用.目前所使用的矫直设备不同程度提升了矫直的性能与适用范围,其中部分矫直机的生产已经实现了系列化,标准化.根据被矫直材料的形状主要分为管材矫直机和棒材矫直机,其中棒材矫直机又分为多辊矫直机和二辊矫直机.管棒材矫直机都是采用反弯矫直原理,依靠管棒材在前进中所受塑性弯曲连续变化实现矫直,但是辊系、辊数、辊距及下压量等参数需根据实际情况确定[1].文献[2-3]中提出影响线材矫直过程精度的主要影响因素,研究了主弯曲辊作为矫直工具的平行辊线材矫直模型,但未针对性的给出矫直关键工艺参数.文献[4]对有关矫直技术理论的研究做出了大量贡献,在线材矫直方面,详细阐述了旋转反弯矫直的原理,但旋转反弯矫直对材料自身损害较大,不适合微细铝丝的矫直.文献[5]给出一种钢丝辊式矫直器的参数计算公式,可为文中铝丝矫直相关参数计算提供依据,但文中没有提供矫直装置的结构与详细实验,且矫直材料的属性不同,只可作为参考.文献[6]通过计算机数值模拟技术对辊式矫直机的矫直过程进行了仿真,可对矫直机的设计与实际矫直起到指导作用.本文以微细铝材的连续矫直为研究对象,根据矫直的基本原理,按照连续矫直、对材料损害较小的要求原则,对矫直的主要工艺参数进行优化.
1 辊式矫直原理
金属矫直是利用其反弯、弹复与残留三种曲率变化的内在关系,通过弹复曲率与反弯曲率的合理匹配,使残留曲率达到零值,其结果称为矫直[7].平行辊矫直机工作原理是根据材料原始弯曲程度,在一次弹复后残留弯曲程度的减小,使残留弯曲趋于一致,在后续各辊的矫直作用下,残留弯曲逐渐减小趋于零值.辊式矫直原理如图1所示,根据矫直目标材料的不同,需得出相应的辊径D、辊距t、辊数n与合适的下压量便可实现目标材料矫直的效果.
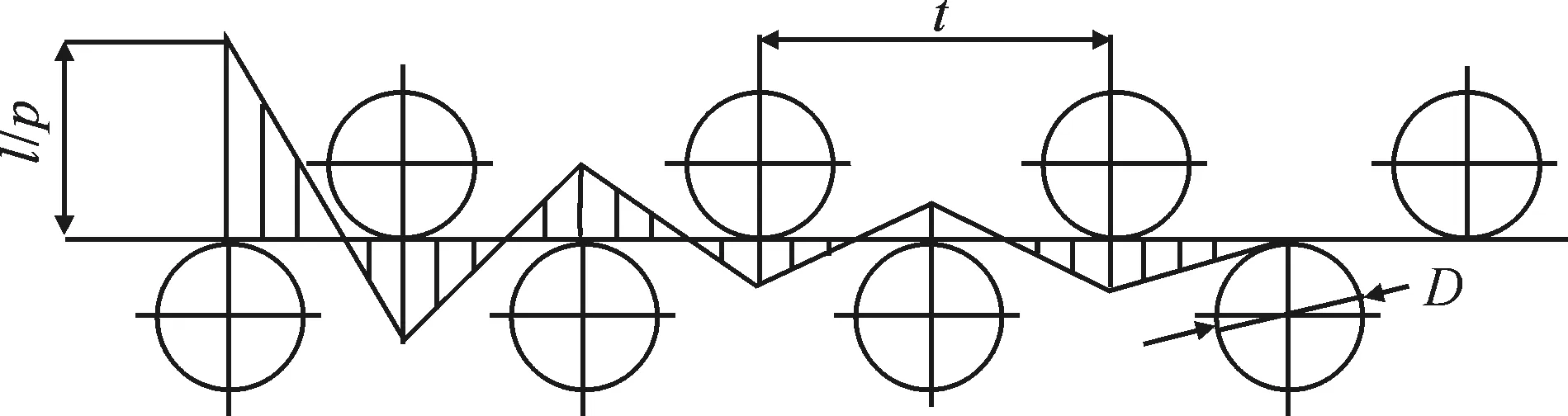
图1 辊式矫直原理示意图
1.1 弹塑性弯曲曲率
如图2所示,取单位长为oa的圆弧,设原始状态弯曲曲率半径为ρ0,弧长为oa=1,对应的弧心角A0为
A0=oa/p0=1/p0
(1)
弧oa的曲率用1/ρ0表示,由式(1)可看出曲率在数值上也可以用A0表示,材料的原始曲率在数值上用原始曲率角A0表示.图2所示对弧oa条材进行反弯达到弧oa1状态,形成的反弯曲率角为Aw,相应的反弯曲率半径为ρw.弧oa由弯到Aw成为弧oa1状态,总的曲率角变化量为A∑=A0+Aw.当外力撤销后,条材将形进行弹复,此时弧oa2所对应的残留曲率角为Ac.图2中左侧的ρ0与ρc两个半径线间的夹角,即条材的弹复曲率角Af=Aw-Ac.弹复后的材料与初始状态之间的差别处于稳定状态,变形为永久变形,所对应的变形曲率角为As=A0+Ac.从工件曲率的角度分析工件矫直所必需的条件,在工件的反弯过程中,当工件反弯后弹复变直时,Ac=0,即为Aw-Af=0,即为矫直时的曲率方程式.因此,为使工件矫后变直,须选用一个与弹复曲率相等的反弯曲率.
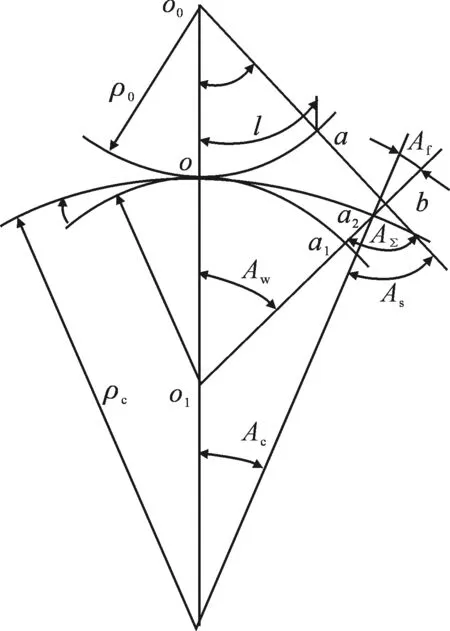
图2 弯曲时曲率变化
1.2 弹塑性弯曲与弯矩的关系
弯曲时,圆形断面按理想金属材料计算的弹塑性弯矩为[4]:

(2)
弯矩与曲率比的关系式:
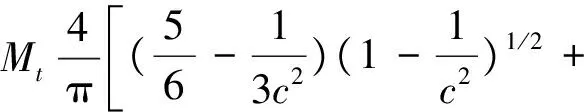
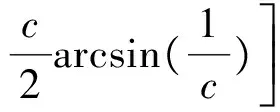
(3)
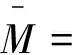
(4)
2 矫直器选型及结构参数确定
对于盘条材料的矫直,在生产中矫直的方法有反弯矫直、拉伸矫直、拉弯矫直和旋转矫直等,而拉伸矫直和拉弯矫直法矫直效率偏低不太适合盘条材料的高效矫直,旋转矫直虽然可以实现盘条料的矫直,但对微细线材自身损害严重且生产效率较低,文中选用反弯矫直法矫直.
平行辊矫直机为连续性反复弯曲的矫直设备,辊式矫直的理论基础是金属材料在较大弹塑性弯曲条件下,其原始弯曲在弹复后残留的弯曲会显著减小,甚至会趋于一致.随着压弯大程度减小其弹复后的残留弯曲必然会一致趋近于零值而达到矫直的目的[8-9].平行辊矫直系统具备两个基本特征,一是为实现反复压弯需具有一定数量的交错配置的矫直辊;二是为实现所需要的压下方案,压弯量可进行调节[10].为了对微细铝丝进行矫直,首先需要确定矫直器的选型,其次确定矫直器结构参数.
2.1 矫直器的选型
平行辊矫直辊系结构主要与用途和矫直质量有关.主要有上辊组平行升降辊系用于矫直粗矫板材的,两端辊单独调整辊系用于热矫板材,上辊可调成平行升降,单项倾斜和双向倾斜的一种灵活多用途辊系等,由于材料直径较小,在实际试验中需采用小变形逐步矫直方案确保更加完好的直线度,所以文中选用线性递减的压下的辊系.
由式(4)可得矫直曲率比方程为
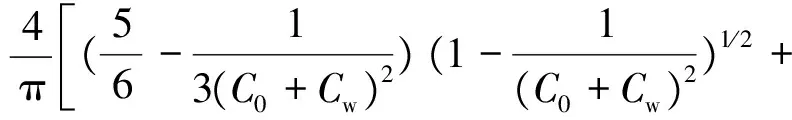
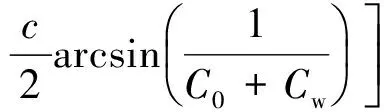
(5)
当材料经过弯曲曲率Cw矫直后会出现弹复现象,弹复曲率为Cf,弹复后残留曲率Cc为弯曲曲率Cw与弹复曲率为Cf之差,即:
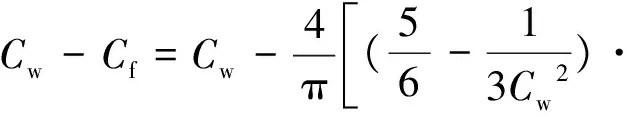
(6)
计算时首先求出压弯曲率;其次求出残留曲率,通过式(5)与式(6)可定量计算出辊数.选择辊数为9的平行辊矫直器.
2.2 矫直器的结构参数
辊径选取的矫直辊,既需要能为工件提供足够曲率的压弯,又需要符合咬入条件并满足强度上的需要.工作辊直径为
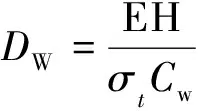
(7)
式中:DW为工作辊直径(取15);CW为常量,通常取4~5.辊距可根据辊径来确定.
t=αDW
(8)
式中:t为辊距(取17);α=1.1~1.2,当辊子单独调节压弯量时辊距常数α取小值,当辊系集体调节时辊距常数α取大值.
矫直辊间的铝丝变形后的波峰与波谷之间的垂直距离为压下量A.在矫直过程中,弯曲曲率半径会逐渐减少,压下量也应逐渐减小,在一定范围内下压量是可以调节的[11].为了满足工艺要求,设计中采用螺纹调节方式.
3 实验验证及分析
3.1 矫直器的结构与实验验证
根据设计参数及其他需求,设计出一组矫直器的结构如图3所示.该矫直器由调节螺栓、辊轮、固定螺母、底板、固定板、移动快及固定块7部分组成.设计核心在于在平面内布置9个辊轮,上排4个辊轮,分别由对应的调节螺栓固定位置,下排5个辊轮,位置固定于固定板上.当铝丝通过矫直器左端进入,通过对调节螺栓1的调节带动移动快6位置的改变,从而调节辊轮之间的下压量,使上下两排辊轮受力,调节过程保证下压量逐渐减小,最终铝丝从矫直器右端出来,完成铝丝矫直.
矫直装置只有在生产加工中满足实际要求才能解决现实问题,因此以实际加工中常用的∅0.35 mm的型材为例进行矫直实验(工作中精度要求≤5 mm/20 cm),矫直前后结果如图4所示.通过对矫直后铝丝抽样200根进行直线度检测得出:材料在矫直前后直线度有明显改变,其中矫直精度在最优结果0~1.0 mm/20 cm之间,为5根占2.5%,精度在1.0~2.0 mm/20 cm之间,为40根占20%,精度在2.0~3.0 mm/20 cm之间,为100根占50%,精度在3.0~4.0 mm/20 cm之间,为50根占25%,刚好满足加工精度4.0~5.0 mm/20 cm之间为5根占2.5%,矫直精度主要分布在1.0~4.0 mm/20 cm之间,为190根占95%,由于矫直器加工过程中的加工误差及矫直过程中震动的影响,虽不能保证所有结果为最优结果,但完全可满足加工要求≤5 mm/20 cm.

图3 矫直器结构

图4 矫直前后对比
3.2 曲率的变化对矫直的影响
圆形条材的Cw-C0曲线图与Cc-Cw曲线图分别如图5~6所示.根据材料原始曲率C0找到最小变形所需矫直曲率,由于各部位原始曲率不同,需最大的C0值矫直,同时将最小的C0值压弯变成下一次矫直的对象即最大的C0值,逐步进行,达到允许残留弯曲时变完成矫直.
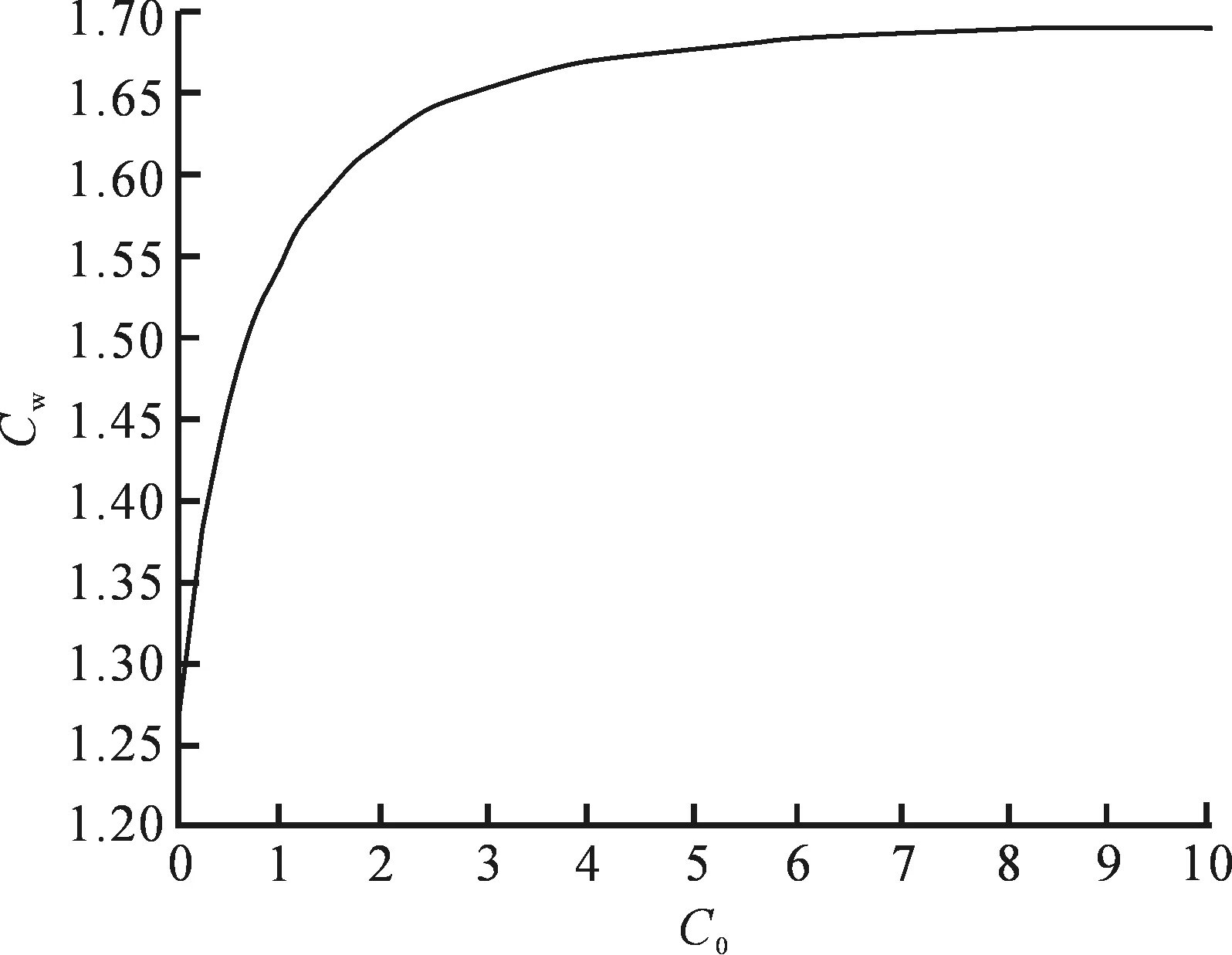
图5 圆形条材的Cw-C0曲线Fig.5 Cw-C0 curve of round bar
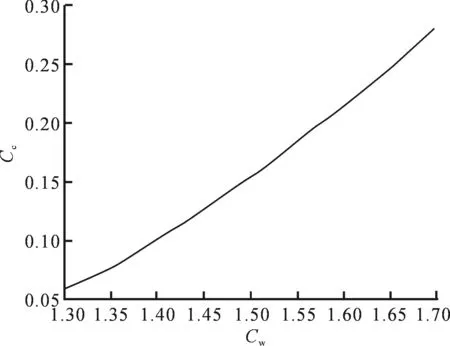
图6 圆形条材的Cc-Cw曲线Fig.6 Cc-Cw curve of round bar
该矫直材料的初始曲率为C0=±2,第一次反弯将其中-2矫直,+2在第二次反弯时矫直.两次反弯所用Cw1=Cw2=1.63(由图5曲线查知).此时残留曲率Cc2=0.24(由图6曲线查知),则C03=Cc2=0.24.最终求得Cc6时可达到矫直要求(即反弯6次,辊数为9).
当σt为材料弹性极限(σt取330 MPa);E为材料的弹性模量(E取69 GPa);H为断面直径0.35 mm.此时残留曲率为Ac6=AtCc6=2σt/EH*0.01,可得到曲率为Ac6为0.000 27 mm,相应的曲率半径为pc6=4 982 mm,直线度约为0.01 mm/20 mm,辊数为9的平行辊矫直器时,采用逐步减小弯曲曲率的方法可满足加工要求.
4 结 论
1) 根据矫直原理,分析辊式矫直中弯曲曲率的不同变化,得出残留曲率与弯曲曲率随着矫直次数的增加将逐渐减小,当材料残留曲率满足加工精度要求时,此时矫直次数合理,可实现材料的矫直.
2) 试验中矫直断面直径为0.35 mm的铝丝,利用平行辊式矫直中逐步减小弯曲曲率的方法,当辊数为9,矫直辊直径为15 mm,辊距为17 mm,下压量依次调节为2.5 mm,2.2 mm,1.7 mm,1.0 mm,可进行有效矫直,满足对材料损害较小且连续矫直的要求.
3) 在微细铝丝的矫直过程中,若在结果检测环节使用在线检测功能,则可针对出丝结果残留曲率的状态对下压量进行及时调节,可以提高矫直精度,减小矫直后直线度范围.
参考文献:
[1]孙兴德.管棒材矫直机的应用及展望[J].金属制品,2014,40(4):39.
SUN Xingde.Application and Prospect of Tube and Bar Roller Straightener[J].Metal Products,2014,40(4):39.(in Chinese)
[2]PAECH M.Factors Relating to the Wire Straightening Process and Peripherals[J].Wire Journal International,2002,35(12):64.
[3]GUERICKE W,PAECH M,ALBERT E.Simulation of the Wire Straightening Process[J].Wire Technology International,1996,63(752):613.
[4]崔甫.矫直原理与矫直机械[M].北京:冶金工业出版社,2007
CUI Fu.StraighteningTheory and Straightening Machine[M].Beijing:Metallurgical Industry Press,2007.(in Chinese)
[5]张焰辉,赵敏杰,贺吉良.一种简单实用的钢丝辊式矫直器[J].金属制品,2000,26(5):35.
ZHANG Yanhui,ZHAO Minjie,HE Jiliang.A Simple and Practical Roller-Typed Straightener[J].Steel Wire Products,2000,26(5):35.(in Chinese)
[6]孙登月,许石民,周慧峰,等.Q46020号角钢9辊矫直过程有限元仿真[J].钢铁,2009,44(9):56.
SUN Dengyue,XU Shimin,ZHOU Huifeng,et al.FEM Simulation of Q460 No.20 Angle Beam Straightening Procedure on Nine Roll Straightener[J].Iron and Steel,2009,44(9):56.(in Chinese)
[7]崔甫.矫直技术与理论的新探索[M].北京:冶金工业出版社,2014.
CUI Fu.A New Exploration of Straightening Theory and Technology[M].Beijing:Metallurgical Industry Press,2014.(in Chinese)
[8]周丽娜.拉伸弯曲矫直机及应用中常见问题分析[J].中国冶金,2005,17(9):20.
ZHOU Lina.Tensile-bending Leveller and Its Problems in Its Application[J].China Metallurgy,2005,17(9):20.(in Chinese)
[9]张子骞,颜云辉,杨会林,等.薄壁管材连续矫直拉伸失稳极限弯曲半径模型[J].钢铁,2014,49(6):55.
ZHANG Ziqian,YAN Yunhui,YANG Huilin,et al.Limit Bending-Radius Model of Tensile Instability for Continuous Straightening a Thin-Walled Tube[J].Iron and Steel,2014,49(6):55.(in Chinese)
[10]冯晓若.圆材矫直的理论与实践[J].山西机械,2002(2):34.
FENG Xiaoruo.Theory and Practice for Bar Straightening[J].Shanxi Machinery,2002(2):34.
(in Chinese)
[11]伍维民.钢丝矫直器的设计[J].金属制品,2006,32(2):46.
WU Weimin.Design of a Wire Straightener[J].Metal Products,2006,32(2):46.(in Chinese)
