基于双光楔的双模光学系统设计分析
2018-04-09李福巍张运强潘国庆
李福巍 张运强 潘国庆

摘 要: 在導引系统中, 将双光楔结构与双模复合光学系统相结合, 使复合光学系统保持不动, 通过双光楔的运动来实现系统的扫描和跟踪。 这种设计不仅简化了位标器的设计, 也给复合光学系统的设计提供了足够空间余量, 有利于导引系统的总体设计。 本文提出一种基于双光楔的红外/激光双模光学系统设计方案, 可用于获取目标的双模信息, 分析了光学系统的基本参数, 研究了采用双光楔结构对扫描视场的实现方法, 并对整体光学系统进行了设计。 所设计系统实现了红外和激光双波段的良好成像, 满足导引系统的使用需求。
关键词: 光学设计; 双模光学系统; 双光楔
中图分类号: TN219; TN249 文献标识码: A文章编号: 1673-5048(2018)01-0043-04
0 引 言
在现代化空天战争中, 精确制导武器成为实施毁灭性打击的重要手段。 目前, 精确制导武器导引制导方式主要包括红外制导、 激光制导、 雷达制导等。 随着未来战争环境越来越复杂, 攻防对抗越来越激烈, 精确制导武器的打击能力受到严重的影响, 多模复合制导方式得到了快速的发展, 这种方式不仅提高了抗干扰能力和复杂战场环境下的命中精度, 同时具备打击多种目标的能力, 提高武器作战灵活性和作战效能[1]。
目前, 多模复合制导技术中最常见的是双模制导技术, 在导弹上应用和正在发展的双模制导技术主要包括雷达/红外、 雷达/电视、 紫外/红外、 可见光/红外、 毫米波/红外和红外/激光等。 其中红外成像/激光成像复合制导技术是该领域的一个重要分支[2]。
然而, 由于两种制导方式的复合必然会增加光学系统的体积和重量, 从而增加导引系统位标器的设计难度, 特别是对位标器的空间布局和响应速度有很大的影响。 因此, 本文考虑将双光楔结构与双模复合光学系统相结合, 使复合光学系统保持不动, 通过双光楔的运动来实现系统的扫描和跟踪。 这种设计简化了位标器的设计, 并给复合光学系统的设计提供了足够空间余量, 更有利于系统的总体设计。
1 双模复合光学系统参数确定
1.1 系统设计思路
目前较为常用的位标器结构有双框架式和横滚俯仰两轴式等, 光学系统一般要安置在某个框架上, 随框架进行运动, 达到对目标搜索和跟踪的目的。
然而, 这样的结构对光学系统的重量和尺寸有较为严格的要求, 限制了光学系统的设计, 特别是双模光学系统, 由于要将两个波段融合在一起,
必然要增加体积和重量, 影响位标器的跟踪速度和响应能力等, 从而给位标器设
计带来压力。
因此, 本文利用光楔对光线的偏折特性, 通过双光楔旋转实现系统的扫描和跟踪, 仅采用两个转动机构, 负载两个光楔进行运动, 极大地简化了位标器的设计; 同时, 这样设计使后面的光学系统与弹体固定在一起即可, 不需要随运动机构进行运动, 从而不需要对光学系统进行严格的尺寸和重量控制, 为其提供了较大的设计裕度, 有利于性能的提高。
1.2 系统性能指标
1.2.1 红外分系统技术指标
(1) 红外接收系统视场: 5°×4°。
(2) 中波致冷面阵探测器, 像元中心距: 30 μm×30 μm; 像元数: 320×256。
(3) 工作波段: 3~5 μm。
1.2.2 激光分系统技术指标
(1) 激光接收系统视场: 2°×1.6°。
(2) 近红外探测器, 像元中心距: 30 μm×30 μm; 像元数: 320×256。
(3) 工作波段: 1.57 μm。
1.3 光学参数计算
1.3.1 焦距
焦距计算公式如下:
f ′=d2tanω(1)
式中: ω为半瞬时视场角; d为探测器光敏面尺寸; f ′为光学系统焦距。
计算可得红外接收光学系统焦距为
f ′IR=320×30 μm2tan(5°/2)=109.9 mm
计算可得激光接收光学系统焦距为
f ′Laser=320×30 μm2tan(2°/2)=275 mm
1.3.2 系统入瞳口径
入瞳口径计算公式如下:
DIR=f ′F/#(2)
式中: F/#为系统F数。
红外接收系统F/#由制冷探测器本身决定, 则计算可得红外接收系统入瞳口径为
DIR=f ′F/#=109.9 mm1.88=58.5 mm
激光接收系统入瞳口径与红外接收系统保持一致, 设计时也将其确定为58.5 mm。
2 双光楔参数确定
2.1 光楔偏折原理
光楔是楔角α很小的棱镜, 由于折射角很小, 其偏向角δ公式可以大大简化, 如公式(3)所示:
δ=α(n-1)(3)
2.2 光楔对消色差原理
由于光楔和棱镜都具有色散的特性, 因此, 当发生偏折时要考虑系统的色差, 对于该问题可以采用组合光楔对减小色差的影响[3]。 组合光楔对是由两个不同材料的光楔组成一个光楔对, 楔角大的光楔采用色散小的硅材料, 楔角小的光楔采用色散大的锗材料。 根据公式(4)~(5)建立色散方程:
αGe(nGe-1)+αSi(nSi-1)=β(4)
αGe(nGe-1)VGe+αSi(nSi-1)VSi=0(5)
式中: n为不同材料的折射率; α为光楔的楔角; V为不同材料的阿贝数; β为光束的偏折角度。
本文系统要求扫描范围为±50°, 即要求单光楔对的偏折角度为25°, 利用以上公式可以计算得到: αGe=1.3°, αSi= 12.5°, 确定光楔对如图1所示。
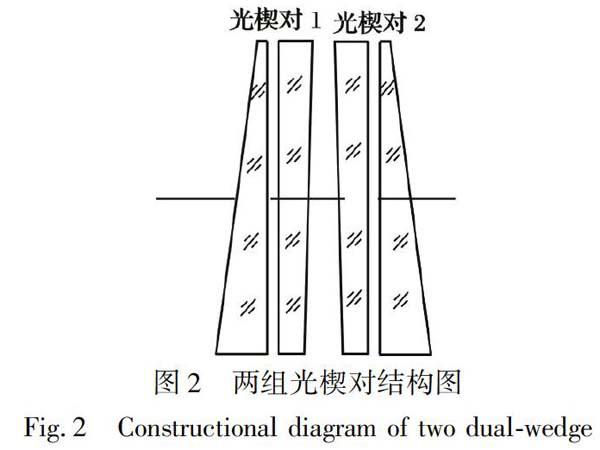
2.3 双光楔对结构确定
根据上文对光楔材料的选择和角度的设计, 确定双光楔对结构, 见图2。 图中位置为偏转角度最大时, 两组光楔对的情况。
根据资料上提到的矢量法, 利用公式(6)计算双光楔对相对运动时光线的偏转情况[4-8]:
φ=2δcos((θ2-θ1)/2) (6)
式中: φ为总偏转角; θ1为光楔对1的转动角度; θ2为光楔对2的转动角度。
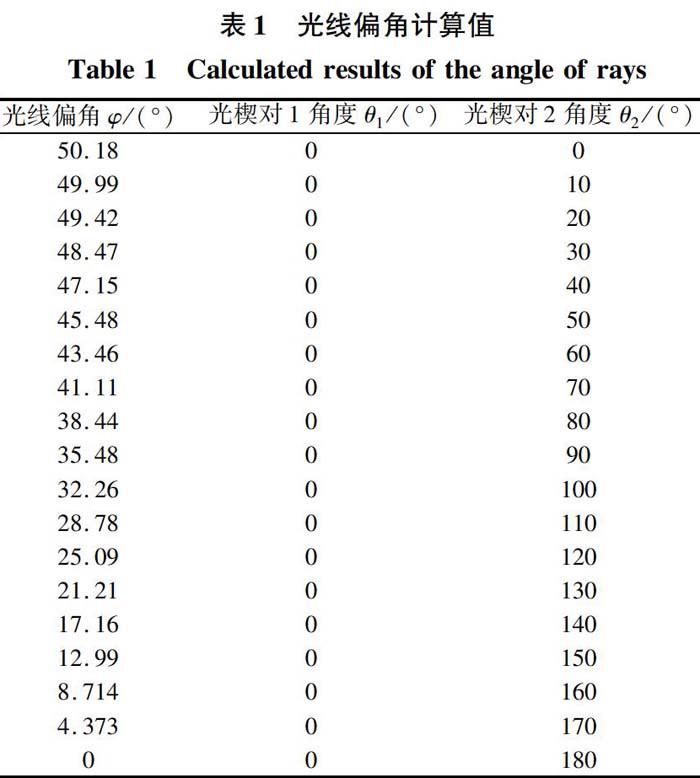
假设光楔对1不动, 光楔对2旋转180°, 以10°为间隔进行计算, 表1为计算得到的光线偏角。
通过光学软件进行光线追迹, 可以得到实际最大偏移量为51°, 达到指标的要求。 图3为光线最大偏向角的情况。 图4为光线最小偏向角的情况, 即无偏向, 仅有一个向下的位移。
3 系统复合设计
3.1 系统结构选择
通过对各种结构形式光学系统的分析, 确定使用透射式结构, 采用一个半反半透的分光镜将两个波段分开, 使光线入射到两个不同的探测器上。
由于系统的搜索视场是由双光楔保证的, 因此, 给光学系统的设计带来了更大的裕度。 不需要严格控制光学系统的长度和重量等, 为系统的优化设计提供了方便。
3.2 设计结果
根据以上设计思想, 利用光学设计软件优化后得到的光学系统如图5所示。
4 设计结果分析
复合光学系统传递函数(MTF)曲线如图6~7所示。 图中不同的曲线表明了不同视场的MTF, 实线为子午方向, 虚线为弧矢方向。 图6为红外分系
统的传递函数, 由于色差的影响曲线距离衍射极限有一定的距离, 但是已经可以满足系统的使用要求。 图7为激光分系统的传递函数, 由于激光为单色光, 没有色差的影响, 其成像质量很好, 已经可接近衍射极限。
5 结 论
本文对基于双光楔的红外/激光双模光学系统设计方法进行了研究, 并设计得到一套可以对红外中波波段和激光波段成像的系统。 该系统以双光楔为扫描机构, 简化了导引系统位标器的设计, 并为光学系统提供了足够的设计余量, 保证了光学系统获得良好的成像质量。 该系统可以满足红外/激光复合成像制导导引系统的使用要求, 为今后该方向的研制工作奠定良好的基础。
参考文献:
[1] 刘代军, 张蓬蓬. 美国下一代空空导弹发展历程与启示[J]. 航空兵器, 2016(2): 3-8.
Liu Daijun, Zhang Pengpeng. Development and Revelation of US Next Generation Air-to-Air Missile[J]. Aero Weaponry, 2016(2): 3-8. (in Chinese)
[2] 李福巍, 张运强, 潘国庆. 红外/激光双模共口径光学系统设计[J]. 应用光学, 2012, 33(3): 496-499.
Li Fuwei, Zhang Yunqiang, Pan Guoqing. Optical Design of IR/Laser Dual-Mode Common Aperture System[J]. Journal of Applied Optics, 2012, 33(3): 496-499.(in Chinese)
[3] 张以谟. 应用光学[M]. 3版. 北京:电子工业出版社, 2008.
Zhang Yimo. Optical Application[M]. 3rd ed. Beijing: Publishing House of Electronics Industry, 2008.(in Chinese )
[4] 郭云曾, 杨小军, 杨小君, 等. 旋转双光楔光路引导系统Matlab仿真研究[J]. 红外与激光工程, 2014, 43(3): 856-860.
Guo Yunzeng, Yang Xiaojun, Yang Xiaojun, et al. Simulation Study of Rotating Double Optical Wedge Vectoring Optics Path Based on Matlab[J]. Infrared and Laser Engineering, 2014, 43(3): 856-860.(in Chinese)
[5] 虞林瑤, 魏群, 张天翼, 等. 无热化旋转双光楔共形光学系统设计[J]. 红外与激光工程, 2014, 43(2): 528-534.
Yu Linyao, Wei Qun, Zhang Tianyi, et al. Design of A Thermal Conformal Optical System Based on Rotated Phase Plates[J]. Infrared and Laser Engineering, 2014, 43(2): 528-534.(in Chinese)
[6] Florea C, Sanghera J S, Aggarwal I D. Broadband Beam Steering Using Chalcogenide-Based Risley Prisms[J]. Optical Engineering, 2011, 50(3): 033001.
[7] Li Anhu, Jiang Xuchun, Sun Jianfeng, et al. Radial Support Analysis for Large-Aperture Rotating Wedge Prism[J]. Optics & Laser Technology, 2012, 44(6): 1881–1888.
[8] 赵军丽, 吴易明, 高立民, 等. 旋转双光楔系统用于像移补偿的技术研究[J]. 红外与激光工程, 2015, 44(5): 1506-1511.
Zhao Junli, Wu Yiming, Gao Limin, et al. Technology Research on Image Motion Compensation of the Rotating Double Optical Wedge [J]. Infrared and Laser Engineering, 2015, 44(5): 1506-1511.(in Chinese)
