过饱和交叉口群自适应控制方法

刘俊杰， 刘雄飞

(中南大学 物理与电子学院,湖南 长沙 410012)

0 引 言

交叉口群由于关联性强，在交通过饱和状态时易造成拥堵堆积，排队溢出，严重降低通行效率，在拥堵性城区的交通优化控制中应当重点考虑。自适应控制算法在交通控制领域的应用已获得广泛关注，具有很大的研究价值[1]。相比绿信比、周期、相位差优化技术(split cycle and offset optimization technique,SCOOT)等集中控制系统，自适应控制更能有效处理交通流的快速变化[2]，文献[3]以单路口排队长度均衡为目标改进了过饱和下的交通控制，但仅避免了单一方向上出现排队溢出的情况，未很好地解决整个路口的拥堵问题。文献[4]采用了动态规划的方法有效改善了单路口的排队长度，但在交通流高峰时期，单路口的优化难以应对可能形成的拥堵堆积问题。文献[5]提出了一种基于多智能体的交通信号控制系统，在小区域内能较好地实现区域协调控制，但其中心化的计算模型缺乏灵活的可扩展性。文献[6，7]提出的自适应算法在交通控制中取得了较好的效果，但基于强化学习算法难以应对复杂交叉口群的情况，易导致维数灾难和不收敛的问题，每个交通路口均需获取所有交叉口数据的设定亦难以应对大的交通网络。文献[8，9]提出了一种不固定相位顺序的单点优化控制方式，为解决固定相位轮转所带来的灵活性问题提供了新的思路。

针对过饱和状态交叉口群易产生拥堵堆积的问题，本文在单点自适应优化控制的基础上提出了以交叉口为中心的区域自治形式的自适应控制方法，根据当前交叉口及其临近交叉口的车辆排队状态，综合确定了当前交叉口的最佳放行相位。

1 区域自适应交通控制

目前，多采用分布式控制方式，将每个交通路口控制器看成代理，除了特殊控制情况，每个交叉口代理拥有独立的控制逻辑，实现自主决策。交叉口代理结构模型如图1。

图1 交叉口代理结构模型

算法设计采用控制—诱导方案，即除基本的交通控制功能外，对交通流进行诱导，在过饱和状态下优先实现车流从拥堵区域向非拥堵区域转移，并抑制车流向拥堵区域聚集。

1.1 车辆检测

目前，广泛采用的检测方式为感应线圈检测[10]。排队长度是过饱和状态判断的关键因素，并以此估计道路的车道占有率，本文采用基于车流量到达—驶离模型计算排队长度[11]。设t(k)为上一阶段绿灯结束时间;t(k+1) 为本阶段绿灯结束时间，排队长度(车辆数)计算公式

l(k+1)=l(k)+marr(k)-mdep(k)

(1)

式中l(k) 为t(k) 时的排队车辆数目;marr(k)为t(k)到t(k+1)期间到达的车辆数;mdep(k)为t(k)～t(k+1)期间驶离的车辆数;车道占有率是排队车辆所占道路长度与道路总长度的比值，用于过饱和交通控制中估计道路的车辆接纳能力。车道占有率为

(2)

式中d为平均车辆长度，本文主要考虑私家车，平均车辆长度取4.5 m[12];g为车辆排队时的平均间距，一般为2 m[13];L为车道总长度。

1.2 自适应算法

算法的关键在于计算交叉口车道的关键系数和放行绿灯时间，关键系数越大，表明该车道对应相位应该优先放行，即该车道为关键车道。关键系数与绿灯时间的计算主要考虑2方面的因素:当前交叉口的车辆排队长度，表示交通流放行的需求强度；对应的下一交叉口的车道占有率，表示下游路口的交通流接纳能力，如果下游路口车道占有率高，即使上游有较大的交通流需求，在放行时也应进行适当抑制，将绿灯时间让给其他车道，否则，可能出现排队溢出的情况，既不利于防治拥堵，也降低了整个路口的绿灯利用率。本文算法综合考虑了上游交叉口的需求与下游交叉口的接纳能力，实现车流的控制与诱导。

如图2示例所示(简单说明，仅考虑了直行)，考虑B交叉口的交通控制，如果只单独考虑B交叉口的交通需求，则应该先放行B→A方向的车流，因为B→A的车流B→C的车流需求大，但实际情况下，此方案明显不合适，A路口进口车道已经临近排队溢出，无法接纳更多的车辆。所以应该综合考虑周边临近路口的交通状态，优先放行B→C方向车流(与相应左转方向组成放行相位)，并且在放行B→A方向车流同时根据A路口进口车道排队情况控制放行时间，抑制交通流向拥堵区域(A交叉口)的堆积。

图2 车流诱导控制示意

1.2.1 关键系数计算方法

关键系数表示各相位的放行关键程度，优先放行关键系数大的相位

p=N×((1-o)+e)

(3)

式中p为相位关键系数;N为排队车辆数量;o为下游路口车道占有率;e为绿波带系数。

当下游路口绿灯剩余时间较长时，可能形成绿波带，能够加快车辆的通过，减少停车次数和行程时间，对于此类相位，在放行优先程度上，应该给予一定的考虑。绿波带系数具体计算如下

(4)

式中tgreen为下游交叉口对应车道的剩余绿灯时间，若为红灯，则为0;L为下游车道长度;vavg为平均车速。当tgreen×vavg-L>0时，表示车辆以平均速度行驶至下一路口时仍是绿灯，即能够形成绿波带。

1.2.2 绿灯时间的计算方法

理想的绿灯时间应刚好使所有排队车辆以及在绿灯期间到达的车辆通过交叉口。考虑到过饱和状态下下游交叉口可能出现局部拥堵导致道路占有率高的情况，绿灯时间应同时考虑下游车道的车辆容纳能力,即放行车辆N为

N=min(mque+marr,macc)

(5)

式中mque为本车道当前排队车辆;marr为绿灯期间可能达到的车辆，根据上一周期的车辆到达情况进行估计;macc为下游车道可接纳的车辆数量，需要根据车道长度和车道占有率估计

(6)

以一次迭代的方式计算放行绿灯时间，分为2步:

1)设绿灯期间可能到达的车辆数marr=0，计算初始绿灯时间

t0=tSULT+N0×H

(7)

式中tSULT为启动延误;H为饱和车头时距;N0为设marr=0时由式(5)计算出的初始车辆数量。

2)根据t0估计marr，得到绿灯期间可能到达车辆数量

(8)

式中tred为该相位刚刚结束时红灯时间长度。由式(5)计算出考虑marr时总的放行车辆数N，再由t=tSULT+N×H计算最终的绿灯放行时间t。

1.2.3 算法流程

在相位方案设计时，为简化计算，根据实际情况，不考虑右转车流以及行人流，根据双环结构的原理，交叉口8个相位(直行与左转)中，每次至多只能放行2个相位，如图3所示，2个相位必须位于不同的组中，而且处于同一个屏蔽中。一个交叉口所有可能的相位组合如相位1～相位8。

图3 相位双环结构

算法基本思路是根据各相位的关键系数对相位的关键程度进行排序，优先放行排序靠前的相位。在确定放行相位之后，根据绿灯时间计算方法计算放行时间。绿灯结束时需重新计算相位关键系数并排序，确定下一组放行相位。在一个循环中已经放行过的相位不再优先考虑，且每个相位在一次循环中必须至少被放行1次，以确保不会有某个方向的车辆等待过长时间的情况。算法流程如图4所示，图中双线箭头表示实际绿灯放行时间。

图4 交通控制算法流程

算法流程中所指的次相位选择规则如下，首先判断Q1，Q2是否均在排队队列中，不在队列中表示此相位在本轮循环中已经放行。若Q1，Q2均在或均不在队列中，则选取关键系数排序在前的作为次相位；否则，选取在队列中的相位作为次相位。

算法中，TM-TQ≤Tmin(Tmin为最小绿灯时间)用于判断如果主相位与次相位的绿灯时间差别不大，则主次相位共同放行主相位的绿灯时间；反之，说明主次相位绿灯时间差别过大(实际上即表明交通流差别过大)，如果此时仍按照主相位较长的绿灯时间放行，容易造成次相位的空等或者不合理放行，则考虑先将主次相位以次相位的绿灯时间共同放行，再将主相位与另一个与之匹配的相位进行组合，形成新的放行组合，放行时间取主相位剩余放行时间和第二次相位放行时间中较大者，以此提高绿灯时间利用率。

算法在相位确定需要放行之时计算绿灯时间，区别于更加灵活的实时绿灯时间调整方式，在绿灯放行期间内，绿灯时间不会再发生变动；1)可以避免随机因素造成的绿灯时间的随意抖动；2)可以更加人性化的确定绿灯倒计时。另外，考虑到行人因素和避免某一方向过长时间的等待，所有绿灯时间均必须处于最小绿灯时间和最大绿灯时间之间。

2 仿真评价

2.1 仿真模型

采用德国PTV公司的VISSIM交通仿真软件进行仿真测试，并通过VISSIM的COM编程接口连接微软.net开发平台进行控制算法设计与开发，相比VISSIM原生的VisVAP编程，能够更加灵活地对交通模型实现算法控制。

为充分考虑交叉口群的相互作用，设计了一个4×4的仿真路网，图5仅表示了仿真路网的拓扑结构，实际仿真路网的道路设置并不具有这样的高度对称性。车流从路网四周驶入，根据不同交通状态设计不同车流量进行仿真。流量设计包括过饱和，低饱和以及短时高峰流量3种。根据文献[13]的分析，设置启动延误时间为5 s，饱和车头时距为2.2 s/veh(veh：辆)，根据实际工程经验，设置最小绿灯时间为15 s，最大绿灯时间为60 s。

图5 仿真路网

不失一般性，对路口进行评价时，选取1#,2#,3#,4#共4个路口的评价数据。仿真时间为0～4 200 s，VISSIM仿真开始时车辆需要一段时间进入路网，难以准确模拟实际情况，所以0～600 s在评价时不考虑，以600 s为统计时间间隔。仿真基本参数为VISSIM默认设置。

本文仿真时在各路口设置了排队长度检测器，并选取左上角S点为检测起点，随机选取A,B,C,D共4个点为检测终点，用于检测从S点出发的车辆分别到达4个终点时所需要的行程时间。本文以排队长度为主要评价指标[10]，评价自适应算法对拥堵的控制效果，并参照行程时间分析算法提升整体路网运行效率的效果。

2.2 过饱和情况下的交通评价

设置过饱和情况下的道路入口流量为800 veh/h，固定配时和自适应控制下最大排队长度，平均排队长度的对比，分别如图6和图7所示。排队情况图中，每个时间段内分别有1～4共4个路口的排队数据，下同。

图6 过饱和下最大排队长度

图7 过饱和下平均排队长度

分别按照仿真时段和路口考察自适应算法的优化效果,如表1和表2。时段优化效果指特定时段下，4个路口的排队长度优化效果平均值；路口优化效果指该路口所有时段的优化效果平均值。

表1 过饱和下排队长度时段优化效果 %

表2 过饱和下排队长队路口优化效果 %

最大排队长度能够反映交通流量过饱和时拥堵高峰时期车辆堆积的严重程度，平均排队长度反映了一段时间内交通的整体拥堵状况。由图6、图7可以看出，在过饱和交通状态下，本文提出的自适应控制方法有效控制了车辆的拥堵，尤其对于第3路口，固定配时由于不能根据实际情况进行信号灯的调整，不合理的分流导致排队堆积，形成了严重的交通拥堵，而自适应算法则较好地对拥堵进行了抑制和疏散。

2.3 低饱和与短时高峰流量情况下的交通评价

低饱和情况下道路入口流量为200 veh/h，短时高峰流量情况下的流量输入由程序随机生成，流量从均值400 veh/h按时间段逐步增加到800 veh/h，再逐步减少。仿真结果所得到的优化效果如表3和表4所示。

表3 低饱和与短时高峰流量下平均排队长度时段优化效果

表4 低饱和与短时高峰流量下平均排队长度路口优化效果 %

从表3和表4可以看出，自适应交通控制算法不仅在过饱和情况下能有效抑制拥堵，在低饱和以及短时高峰流量情况下，自适应算法对车辆排队的改善同样具有明显效果，优化效果一般在30 %以上。在低流量情况下避免了空等现象的发生，在车流量逐渐增加的过程中，也能通过各路口对车流量放行灵活分配，降低了路网出现严重拥堵的可能性。

2.4 整体路网交通状况评价

排队长度能够有效反映交通拥堵的状况，但对于司乘人员，行程时间是实际出行时最关心的数据，如图8和表5分别为4条行程时间统计线路的仿真数据，线路包含了仿真路网中大部分的交叉口，可以反映整体路网的交通状况。

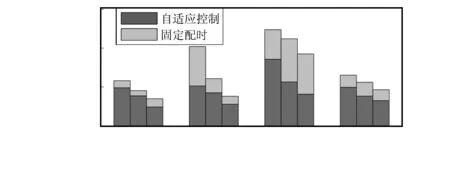
图8 行程时间

状况S-AS-BS-CS-D过饱和流量16503124短时高峰流量15305032低饱和流量30275630

图8中横轴表示各测试线路，每条线路从左到右的条形图分别表示过饱和流量，短时高峰流量，低饱和流量下的行程时间数据。仿真实验结果表明:自适应控制下各条线路的行程时间均有所缩短，行程时间平均减少了32 %，部分线路减少了50 %以上，即行程时间只有定时控制时的1/2。由此可以看出，自适应控制方法在控制交通拥堵的同时，有效提升了路网整体交通通行效率和绿灯时间的有效利用率。

3 结束语

提出了一种区域自治的自适应控制方法，以车辆排队长度为参数，实现当前交叉口与临近交叉口的协调控制，与传统单点优化相比，改善了仅优化局部的情况，去中心化的控制方式亦提高了系统的灵活性。仿真结果表明：控制方法在过饱和状态交叉口群的交通情况下，较为有效地控制了拥堵的持续堆积并加快了拥堵的疏散，缓解了拥堵的扩大趋势。在非饱和交通状态下，较定时控制，自适应控制方法相比，同样有效提高了绿灯时间利用率，缩短了车辆行程时间，提升了交叉口群的整体交通运行效率。

参考文献:

[1] Wunderlich R,Liu C,Elhanany I,et al.A novel signal-scheduling algorithm with quality-of-service provisioning for an isolated intersection[J].IEEE Transactions on Intelligent Transportation Systems,2008,9(3):536-547.

[2] 赵冬斌,刘德荣,易建强.基于自适应动态规划的城市交通信号优化控制方法综述[J].自动化学报,2009(6):676-681.

[3] 张 龙,余发山,康 洪,等.过饱和单交叉口信号配时控制算法的研究[J].电子测量技术,2016,39(5):150-153.

[4] 李瑞敏,唐 瑾.过饱和交叉口交通信号控制动态规划优化模型[J].交通运输工程学报,2015,15(6):101-109.

[5] 曹 洁,张 玲.自适应遗传算法的Multi-Agent交通信号优化控制[J].计算机工程与应用,2016,52(13):265-270.

[6] Balaji P G,German X,Srinivasan D.Urban traffic signal control using reinforcement learning agents[J].IET Intelligent Transport Systems,2010,4(3):177-188.

[7] Arel I,Liu C,Urbanik T,et al.Reinforcement learning-based multi-agent system for network traffic signal control[J].IET Intelligent Transport Systems,2010,4(2):128-135.

[8] 赵亚东,吴其龙.基于VisVAP的过饱和交叉口群自适应控制评价[J].电子科技,2016,29(3):17-21.

[9] 张永灿,黄海平,曹 雍，等.基于无线传感网的智能交通灯自适应算法[J].计算机技术与发展,2015(2):199-203.

[10] 彭春华,刘建业,刘岳峰,等.车辆检测传感器综述[J].传感器与微系统,2007,26(6):4-7.

[11] Liu H X,Wu X,Ma W,et al.Real-time queue length estimation for congested signalized intersections[J].Transportation Research:Part C:Emerging Technologies,2009,17(4):412-427.

[12] 孙 剑,杨晓光,刘好德.微观交通仿真系统参数校正研究[J].系统仿真学报,2007,19(1):48-50.

[13] 赵 星,任 刚.信号交叉口车头时距特性分析[J].交通运输工程与信息学报,2010(1):103-108.