基于CCA空间的平滑稀疏超分辨率人脸重构*

姚正元, 郭立君，张 荣

(宁波大学 信息科学与工程学院，浙江 宁波 315211)

0 引 言

对于监控视频中的人脸图像，往往因为光线不足，人脸距离监控设备过远等原因而变得模糊不清，充满噪声。为此，有必要利用先验信息，提升人脸图像的分辨率。

单帧图像的超分辨率(super-resolution,SR)重构问题中，基于学习的SR重构方法成为近年来研究的重点。 Baker S和Kanade T[1]首次提出了“人脸幻构”概念。Liu C等人[2]提出了两步法，将一个全局的参数高斯模型和一个局部的非参数的马尔科夫随机场(Markov random field,MRF)模型整合。此后，研究开始集中于利用包含高低分辨率图像对的训练集，从单个的低分辨率(low-resolution,LR)人脸图像重构出高分辨率(high-resolution,HR)图像。此类方法，包含基于全局的人脸图像或者基于块来重构HR图像。

基于块的人脸SR方法是通过对训练集中的块线性组合，来重构测试的低分辨率块。为了获得更多的面部结构的先验知识，Ma X[3]提出了一种基于块位置重构人脸图像的框架，方法基于最小二乘表示(least squares representation,LSR)用所有的训练块重构图像块。为了克服LSR的不稳定性，Yang J等人[4]首次提出了基于稀疏表示的人脸图像超分辨率方法,此后，Wang Z Y等人[5～9]提出了一种加权的稀疏表示人脸超分辨率方法。为了进一步探索局部图像块的关系，Shi J[10]提出了将全局重构模型，局部稀疏模型和像素相关模型组合成统一的正则化框架，展现了一种新的超分辨率重构方法。

上述SR重构方法在人脸超分辨率问题上取得了很大的成功，但对于视频监控中的人脸图像，往往充满噪声。为了解决这个问题，Jiang J等人[11～13]提出了一种基于块的局部约束模型(local constraint model,LCR)。在此基础上，Jiang J[14]提出了一种基于平滑的超分辨率重构方法(smooth SR,SSR),取得了一定的平滑与去噪效果。乔少华等人[15]提出了一种基于统计量的加权函数图像重建方法,对含有多种噪声的退化图像能够取得比较理想的结果。Jiang J等人提出的重构模型都是基于高低分辨率字典是高度相关,并且有相似的结构分布这一假设，但直接基于人脸图像空间构建的高低分辨率字典无法满足高度相关的条件，影响了重构的效果。

本文提出了基于典型相关分析(canonical correlation analysis,CCA)空间的平滑稀疏超分辨率重构算法，利用先验信息中人脸图像存在相似性这一特点，将2组字典映射到CCA空间，增强2组字典之间的相关性，最大限度地利用图像之间的关联信息，增强了高低分辨率字典的相关性，进而利用高低分辨率字典的信息，剔除冗余和噪声成分，增强对噪声的鲁棒性。同时，为了达到更好的CCA映射，获得增强相似性的效果，进一步提出了基于排序和更新的字典优化方法：在重构过程中，与输入块更相似的训练块应该被给予更大的重构权重，对字典按照和输入图像块的相似性从高到低进行排序；为了去除噪声和冗余，对于排序后的字典，对字典进行一次稀疏更新；对于优化过的字典，再次进行CCA映射。实验结果表明：所提算法重构效果更加清晰，对噪声鲁棒性更好。

1 所提方法

1.1 稀疏表示

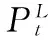
图1 按位置划分的人脸图像

对于一个LR观测的人脸图像的图像块xt，使用训练集中在相同位置的所有的训练块表示

(1)

式中ε为重构误差。最佳的重构系数能够通过式(2)的约束最小二乘问题解决

(2)

式中w=[w1,w2,…,wN]T为对于LR观测块xt的N维重构权重向量。

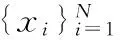
(3)

式中 ‖·‖1为l1范数；λ为正则化参数，用于平衡重构误差和重构系数的稀疏性。该稀疏约束不仅保证欠定方程具有确切的解，并且学习出的稀疏系数w对于输入块能够有效捕捉块最突出，最有效的信息。

上述重构过程并未考虑在实际中高低分辨率字典并不是高度相关的问题，因此，在人脸稀疏重构中引入了CCA空间。

1.2 CCA

当数据集是多维数据集时，CCA采用线性变换，将数据集从多维降为一维，再用相关系数进行分析。对于CCA方法，选择的投影标准是降到一维后，2组数据的相关系数最大。

设X=[x1,x2,…,xN]和Y=[y1,y2,…,yN]分别为输入块xt对应的LR和HR字典。其中，N为字典的向量个数，即原子个数。将2个字典转换到CCA空间。

CCA的目标是分别为低高分辨率字典LR和HR寻找2组基向量α和β，使得经过基向量映射过的字典Xc=αX和Yc=βY之间的相关系数达到最大,即

(4)

取得最大值，其中,E[]表示数学期望。

由于低高分辨率字典X和Y之间存在相似的内在结构，通过其变换到CCA空间，将2个字典之间的线性相关性最大，进而使得2个字典内部拓扑结构的一致性增强。图2为CCA映射过程。

图2 CCA映射过程

1.3 字典优化

在将高低分辨率字典映射到CCA空间之后，虽然字典中的所有字典对的相关性被增强，但是CCA基向量的获取会被字典中的无效块所影响。本文对映射到CCA空间的字典进行排序，对字典进行稀疏更新，再次映射到CCA空间，以进一步增加相关性，过滤掉干扰噪声和冗余信息。

1.3.1 字典排序

对字典中的原子排序，对于和输入图像块更相似的字典中的原子，被排到了前面，并且集中在一起，在重建中能够获得更大的权重。对于噪声和冗余原子等则被集中排在了后面，会获得更小的稀疏权重。根据字典中的图像块和xt的相似度，对字典中的图像块进行重新排序

dist={|αxt-αxi‖1≤i≤N}

(5)

按照相似度从高到低重新标序为Xidx=[x[1],x[2],…，x[i],…,x[N]]，其中,Xidx为原子重新排序的LR字典。[x[1],x[2],…,x[i],…,x[N]]为重新排完序的字典中的原子。X[i]为LR字典里面的第i个原子。

1.3.2 字典稀疏更新

对于排序后的字典，为了达到更优的CCA映射，进一步增强在对输入块的稀疏表示中最重要的图像块对之间的联系，得到优化的CCA映射的基向量，进行一次稀疏更新，训练出一个更加具有代表性，更加紧凑的字典。通过去掉冗余以及不相关的字典对，使重构系数免受干扰。从而对噪声更加鲁棒。

对于输入块xi，可以通过式(6)用LR字典X稀疏表示

(6)

式中w为稀疏系数。 求出的稀疏系数w中的非零项表示的字典的原子组成了排序后的字典Xidx的子集Xs=[x1,x2,…,xi,…,xM]，M为更新后的字典原子的个数。对于优化更新完的Xs，重新计算基向量α。

2 重构过程

对于人脸图像，重构图像的平滑性很重要，但稀疏模型往往忽略图像的平滑性。在CCA映射的基础上，考虑在稀疏模型的基础上加入局部平滑约束项。提出的目标函数为

(7)

第二个约束为平滑约束项，λ2控制稀疏差异约束。对字典中排序后的相邻块的稀疏重构系数加以差异约束，能够达到稀疏系数的平滑性。

重构过程具体步骤为：

1)根据位置将所有的LR和HR的人脸训练图像分块。

2)然后对于输入的每个LR块xt，计算其优化的重构权重。

3)用得到的稀疏系数得到对应的HR图像块

(8)

式中 [y[1],y[2],…,y[M]]为排序后的HR训练图像块。输入的LR人脸图像中全部的图像块按照从左到右，从上到下的顺序读取。

4)对于相邻块的兼容性，对重叠区域的像素值取平均，重构框架如图3所示。

图3 重构框架

3 实验结果与分析

3.1 数据集

人脸数据集FEI如图4，包含200人，100名男士，100名女士。每人有2张图像，正常表情和微笑的表情。裁剪图像成大小为120×100的标准人脸图像。随机选取180人(360张图像)作为训练集，剩下的20人作为测试。在实验中，HR图像首先被下采样到LR的30×25大小的图像，并加上不同等级的高斯白噪声(记作σ，σ=10，30，…)。LR块大小为4×4，HR块的大小为16×16。相邻块的重叠，在LR块中为3像素，在HR块中为12像素。

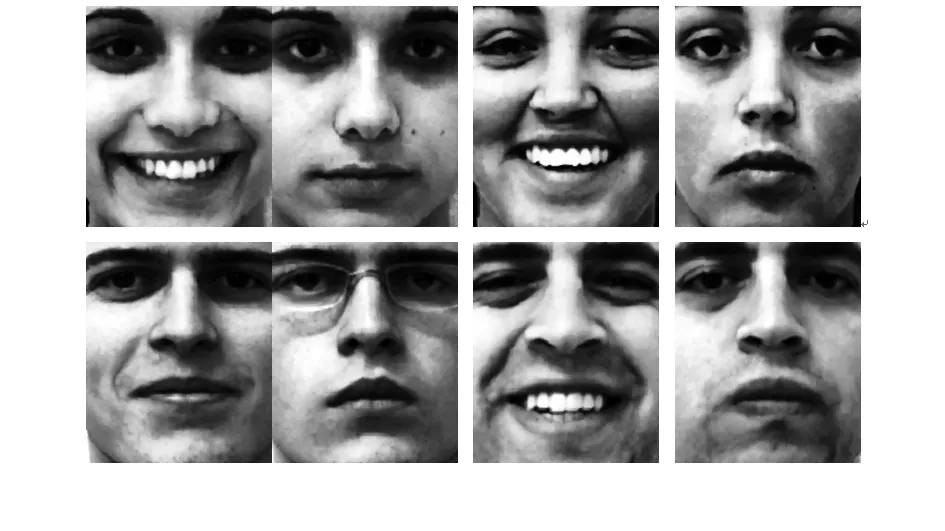
图4 FEI中的一些训练图像

3.2 参数设置

在不同的噪声环境下选取不同的λ1和λ2值的峰值信噪比(peak signal to noise ratio,PSNR)和结构相似度(structural similarity,SSIM)表现。在实验中，σ=10时，选取λ1=1×10-4和λ=1×10-2;σ=30时，λ1=1×10-2，λ2=0.1，以获取最佳的表现。随着噪声的增加，λ2应该被设置为更大的值，表示稀疏差异约束在重构过程中对于平滑和去噪的重要性。

3.3 实验分析

为了度量不同的重构方法的平滑性，比如SR，SSR，定义了一个对于平滑的评价指标平滑指数SI。w=[w1,w2,…，wM]表示一个输入块的稀疏系数。SI定义如下

(9)

图5给出了不同噪声环境下通过SR，SSR方法重构的HR图像通过SR(第二列)，SSR(第三列)和本文方法(第四列)重构的SR图像以及峰值SNR。第一列和最后一列分别是LR人脸图像以及原HR的图像。表1给出了在不同噪声环境下不同方法的平均SI值。由图5可以看出：提出的方法在视觉效果以及重构质量评价均好于SR以及SSR方法；从表1的结果来看，本文方法比SR以及SSR方法更加平滑。

图5 不同噪声下SR,SSR重构HR图像

噪声SRSSR本文方法σ=100.00620.92060.9321σ=300.11840.96980.9744

为了证实提出算法的有效性，对比了SSR方法和本文方法的PSNR和SSIM值。表2给出了测试的40张图像在不同噪声环境下( σ=10,30)的平均PSNR和SSIM。

表2 在不同噪声强度下不同方法分PSNR和SSIM值

4 结束语

提出了一个新的人脸超分辨率重构方法。利用人脸图像之间在结构和内容上都存在相似性这一特点，将人脸训练集映射到CCA空间，以增强对于输入块的两组字典之间的相关性，再通过对字典排序以及字典稀疏更新，训练一个更加紧凑的字典，将字典重新映射到CCA空间，以获取最佳的映射效果。最终，采用平滑稀疏的方法，在稀疏模型的基础上加上平滑约束，完成重构。实验结果表明：相比于现有的最优的人脸超分辨率模型特别是在噪声情况下能够取得理想的提升。

参考文献:

[1] Baker S,Kanade T.Limits on super-resolution and how to break them[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2002,24(9):1167-1183.

[2] Liu C,Shum H Y,Zhang C S.A two-step approach to hallucinating faces: Global parametric model and local nonparametric model[C]∥2001 Proceedings of the 2001，IEEE Computer Society Conference on Computer Vision and Pattern Recognition,CVPR 2001.IEEE,2001:I-192-I-198.

[3] Ma X,Zhang J,Qi C.Hallucinating face by position-patch[J].Pattern Recognition,2010,43(6):2224-2236.

[4] Yang J,Wright J,Huang T S,et al.Image super-resolution via sparse representation.[J].IEEE Transactions on Image Processing，A Publication of the IEEE Signal Processing Society,2010,19(11):2861-2873.

[5] Jung C,Jiao L,Liu B,et al.Position-patch based face hallucination using convex optimization[J].IEEE Signal Processing Letters,2011,18(6):367-370.

[6] Ma X,Philips W,Song H,et al.Sparse representation and position prior based face hallucination upon classified over-complete dictionaries[J].Signal Processing,2012,92(9):2066-2074.

[7] Wang Z,Hu R,Wang S,et al.Face hallucination via weighted adaptive sparse regularization[J].IEEE Transactions on Circuits & Systems for Video Technology,2014,24(5):802-813.

[8] Wang Z Y,Han Z,Hu R M,et al.Letters: Noise robust face hallucination employing Gaussian-Laplacian mixture model[J].Neurocomputing,2014,133(8):153-160.

[9] Qu S,Hu R,Chen S,et al.Face hallucination via Cauchy regula-rized sparse representation[C]∥IEEE International Conference on Acoustics,Speech and Signal Processing,IEEE,2015:1216-1220.

[10] Shi J,Liu X,Qi C.Global consistency,local sparsity and pixel correlation: An unified framework for face hallucination[J].Pattern Recognition,2014,47(11):3520-3534.

[11] Jiang J,Hu R,Wang Z,et al.Noise robust face hallucination via locality-constrained representation[J].IEEE Transactions on Multimedia,2014,16(5):1268-1281.

[12] Jiang J,Hu R,Wang Z,et al.Face super-resolution via multilayer locality-constrained iterative neighbor embedding and interme-diate dictionary learning[J].IEEE Transactions on Image Processing:A Publication of the IEEE Signal Processing Society,2014,23(10):4220.

[13] Jiang J,Chen C,Huang K,et al.Noise robust position-patch based face super-resolution via Tikhonov regularized neighbor representation[J].Information Sciences:An International Journal,2016,367(C):354-372.

[14] Jiang J,Ma J,Chen C,et al.Noise robust face image super-resolution through smooth sparse representation[J].IEEE Transactions on Cybernetics,2016,(99):1-12.

[15] 乔少华,李润鑫,刘 辉,等.基于统计量的加权函数图像重建方法[J].传感器与微系统,2017,36(9):53-56.