覆冰导线均匀和非均匀脱冰跳跃数值模拟研究

2018-04-09王玲君赵诗雅

通信电源技术 2018年1期

俞　凯，王玲君，赵诗雅

(1.上海勘测设计研究院有限公司，上海 200000；2.国网湖北电力检修公司特高压交直流运检中心，湖北宜昌 443001)

0　引　言

当天气变化，或者受到风、外力等不定因素影响时，处于覆冰状态的输电线路将会以各种形式脱冰。目前国内外架空导线脱冰跳跃的研究深度主要停留在覆冰厚度、脱冰方式及风荷载等不同情况下的分析，而从模拟覆冰及脱冰方法本身入手的研究却几乎为零。本文着重考虑了覆冰及脱冰的模拟方法，从根本上解释这些方法的原理及适用范围，并采用有限元法以某大档距跨越段为例，数值模拟覆冰导线非均匀脱冰和均匀脱冰。

1　模拟覆冰脱冰的方法

1.1　等效荷载法

模拟覆冰时，一般把覆冰想象成圆柱形状，则把覆冰简化为圆环截面包裹在导线外面的情况来建立模型。等效荷载法，简而言之，就是将覆冰等效为荷载按实际情况的需要分散在导线的固定或随机点上，来模拟输电线脱冰，分为两大类，即集中荷载和均布荷载，如图1。文献[1]已经验证：采用前者的方法对输电线路覆冰和脱冰跳跃进行模拟，发现输电线的张力以及跳跃高度是符合实际的，因此这种方法也是行的通的[1]。

1.2　质量法

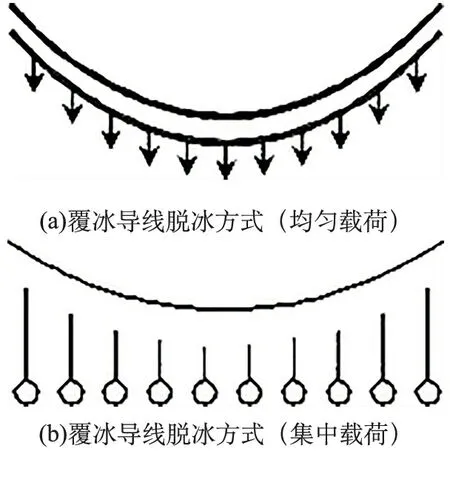
图1　覆冰等效荷载模型

质量法是指对输电线进行动力分析或者静力分析时，仅把覆冰的自身重量考虑在内，而不考虑其它影响。一般在建模计算分析时，将覆冰想象成单元节点处的质量块，可以等效地增加或缩小其本身的质量；如在模拟覆冰时，可以增加该单元处的等效质量块或者按比例增加该单元导线的单位密度；而在模拟脱冰的时候，即可卸载该单元处的等效质量块或者减小该单元导线的单位密度。这种方法容易让人接受,质量块常用Mass21模拟，简单易上手，但是适用范围比较窄，因为只适用于理想条件下的假设。

1.3　Támás模型

质量法和等效荷载法仅把覆冰的自身重量考虑在内，而不考虑其它影响，而实际上覆冰是有一定的机械性能的。为了在模拟时考虑到冰的机械性能对覆冰导线的影响，Támás在研究覆冰的时候，一般用梁单元代替杆单元，并借助有限元法对单档的线路进行研究，分析了当此模型受到破冰器的作用时的动力响应[2]，如图2。

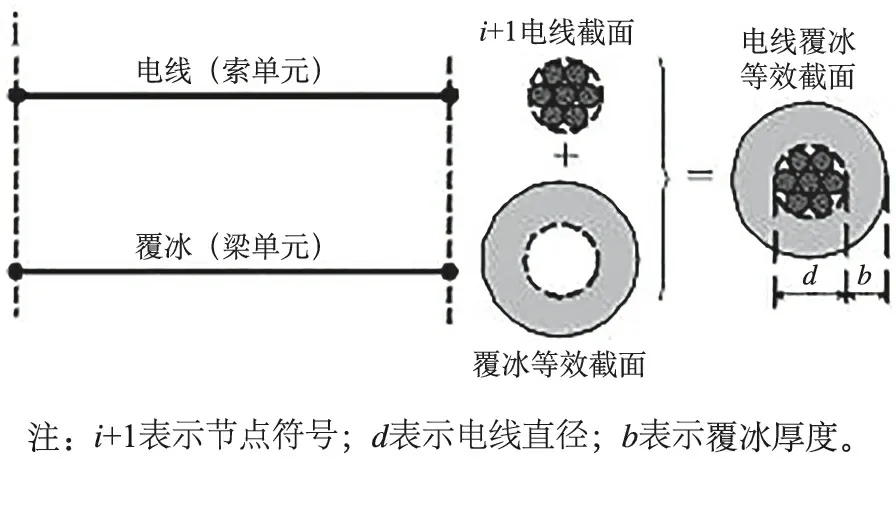
图2　覆冰导线的Támás模型

这种方法在有限元建模的时候需要建立两次模型，首先用索单元或者杆单元来模拟导线，然后用梁单元模拟覆冰，和模拟导线的杆单元共用相同的节点。

1.4　单元生死法

当对一种模型进行研究时，适当的时候需要某个单元或者某些单元不存在，此时利用单元生死法来研究这些问题将会是很好的选择。单元生死其实质就是对单元刚度的设置，需要某单元存在的时候即设其和其它单元一样存在，而不需要它存在的时候，可以设置它不存在，原理是用一个足够小的式子把它的刚度矩阵变为足够小，且其他参数都设置为零[3]。

单元生死法的这种特性刚好贴合架空输电线路中的脱冰现象，所以在日常建模时可借助单元生死法来模拟脱冰。若在导线外面建立覆冰的实体模型时，也可以利用单元生死法的特性，以单元为单位增加覆冰，方便易上手。

以上分析了几种覆冰及脱冰的方法，下面针对第一种模拟方法给出具体的模拟脱冰的算例。

2　算例分析

2.1　导线及覆冰参数

设某单挡导线的水平档距L=1 000 m,导线型号为LGJ-400/35,导线两悬点无高差，导线截面面积S=435 mm2，弹性模量E=6.5×1 010 Pa ,单位质量m=1.349 kg/m,泊松比=0.3，在某气象条件下，覆冰厚度为12 mm,密度取900 kg/m3，导线的水平使用应力为σ=58.27 MPa，导线的材料阻尼比为0.02。

2.2　有限元模型的建立

使用建模软件ANSYS，选择想要研究的导线进行模拟。由于本章只是为了侧重研究模拟覆冰及脱冰方法的脱冰跳跃问题，所以对外荷载的作用不予考虑，仅考虑平面内振动。可以把输电导线视为柔性的悬索结构，由于输电线的截面形状相对于架空输电线的档距要小的多，且输电线一般都由很多条细金属线绞制而成，因此在满足工程需求的同时可以不考虑输电线的刚性影响。在建模软件ANSYS中，LINK10单元特点是受拉压，具有大变形效果，如果将模型划分足够精细，可以满足对导线的模拟。因此本文选取LINK10单元模拟，将导线划分为1 000个单元，建立有限元模型。

2.3　导线的找形

(1) 导线自重找形

借助ANSYS，在研究单根悬索的时候，遇到找形的问题，有两种方法可供选择，分别是直接迭代法或者是找形分析法。本文借助直接迭代法对输电线进行自重找形分析。基本原理：当有限元建模时，可以先建一直线段，进入网格划分阶段只需借助LINK10将其化为足够数量的单元即可，对两端点进行约束并设置真实的材料参数，且将初应变设的足够小，然后加重力加速度并将悬索的张力设成收敛条件，经过一系列迭代更新模型，最后可以完成自重下的找形[4]。

(2) 导线覆冰后的找形

导线覆冰后的找形为二次找形，在自重找形的基础上施加覆冰继续找形，此步骤在ANSYS里利用荷载步进行。用等效荷载法来模拟覆冰，在导线覆冰找形时，以荷载步的方式，施加荷载，亦可确定导线最终的形状，如图3所示，即找形完毕。

图3　导线找形后的最终形状

2.4　覆冰导线非均匀脱冰跳跃的模拟

在现实情况下，覆冰导线的脱冰是比较复杂的过程，均匀脱冰的和不均匀脱冰的情况皆有存在，随机性很强。为了模拟不均匀脱冰的情况，本文采取如图4的方法来模拟覆冰导线非均匀脱冰和均匀脱冰。

图4　覆冰导线均匀和非均匀脱冰的模拟方法

针对相同的例子来模拟覆冰导线非均匀脱冰(50%脱冰)。假设按照图4(a)方式模拟导线脱冰，脱冰仿真时间步长设成0.01 s,仿真时间设成50 s。选取跨中、跨中左侧及跨中右侧代表性节点提取脱冰动力响应的时程位移曲线图。图5(a)给出了跨中节点250处Y向位移时程曲线，图5(b)给出了跨中节点500处Y向位移时程曲线，图5(c )给出了跨中节点750处Y向位移时程曲线。单点跳跃的最大位移见表1。

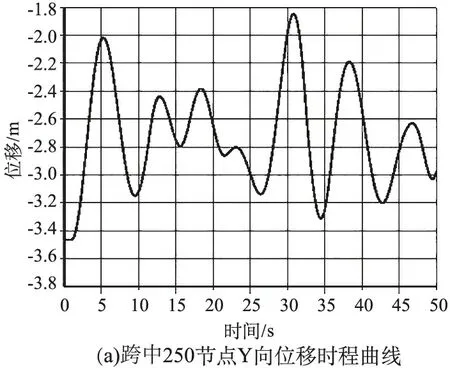
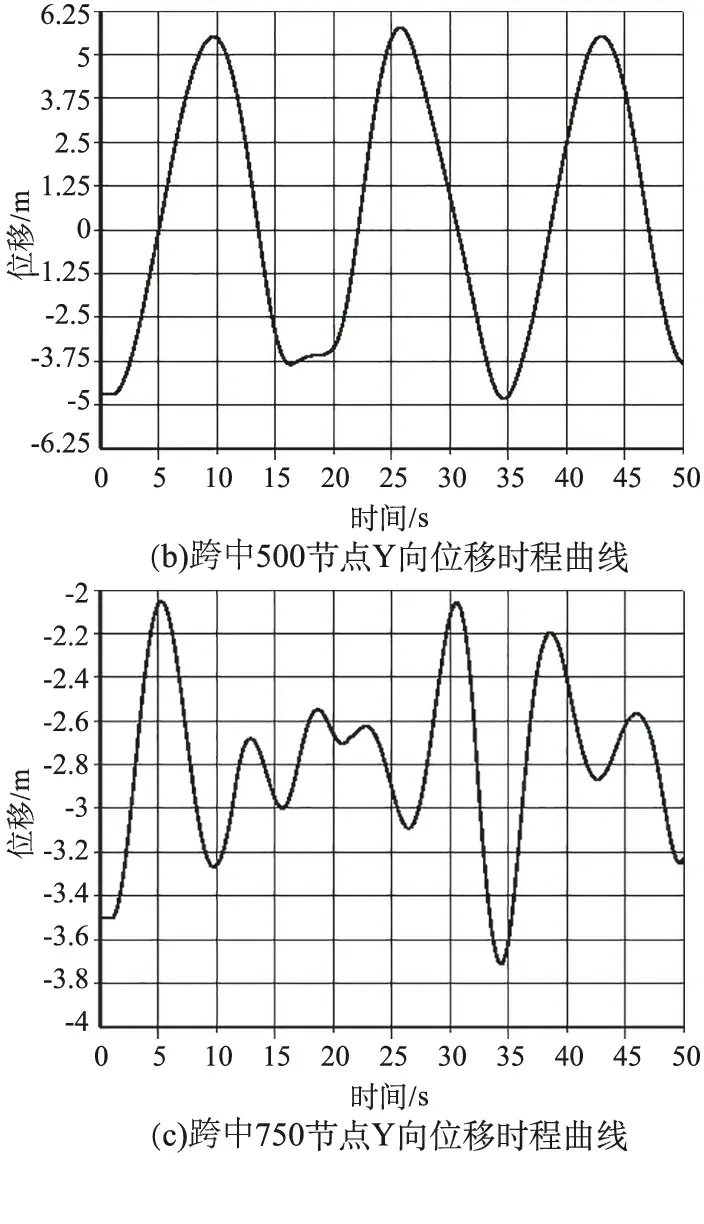
图5　覆冰导线非均匀脱冰模拟结果

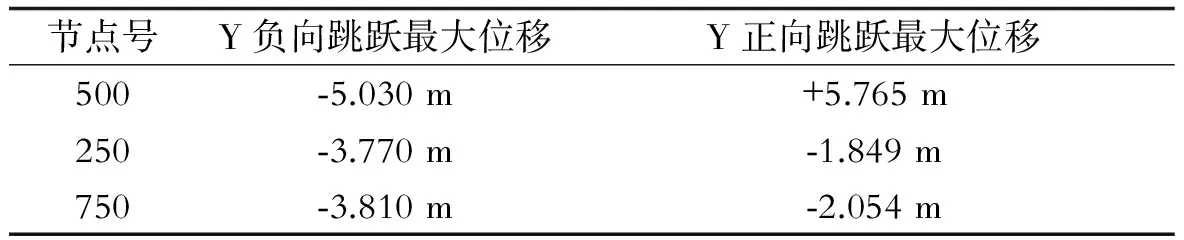
表1　各节点跳跃的最大位移

图6　导线跨中动张力时间曲线

以上是导线脱冰的位移随时间变化的规律，图6是导线脱冰跨中动张力的变化规律。

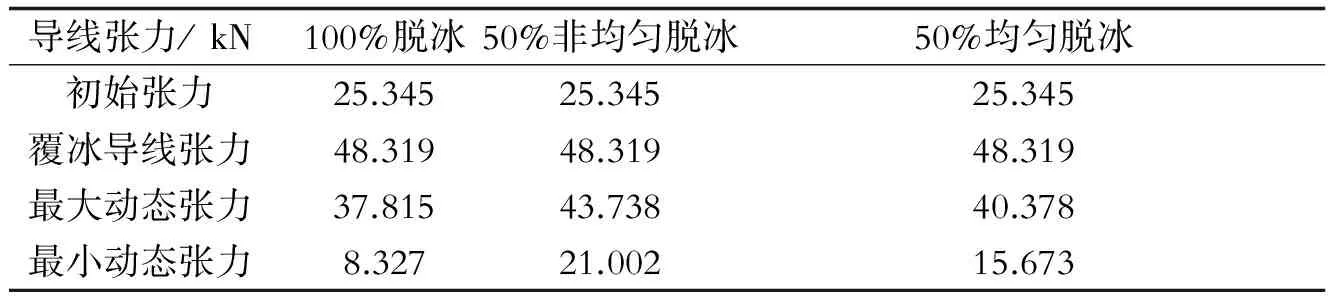
表2　脱冰工况下的导线张力对照表

由导线张力对照表(表2)可以看出导线加覆冰之后张力明显增大，对于导线的脱冰跳跃无论是100%脱冰还是50%脱冰，导线脱冰后跨中张力比覆冰时导线张力要小，三种工况下，50%非均匀脱冰动态张力最大，100%脱冰动态张力最小。同时，导线脱冰的最小动态张力与导线跳跃高度息息相关，导线跳跃高度越大导致最小动张力越小，其实质是由导线的松弛度来决定的。