基于时空关联性的温室环境多传感器数据融合
2018-04-09周金生王纪章王建平李萍萍
周金生, 王纪章, 贺 通, 王建平, 李萍萍,2
(1.江苏大学现代农业装备与技术教育部重点实验室,江苏镇江 212013; 2.南京林业大学生物与环境学院,江苏南京 210037)
近年来,随着信息技术的快速发展,物联网技术在设施农业中得到越来越多的应用[1-2]。传感器技术、无线网络、微型计算机技术、互联网的发展进一步促进了温室环境信息的监测管理[3-5]。为部署温室环境测控系统,须要在温室中布置大量的用于监测温室中主要环境参数的传感器,但是设施农业内部的高湿、高温等恶劣工作环境易导致温室环境测控系统传感器故障的频繁发生。利用传感器采集设施农业内的环境信息是温室环境测控系统的基础,而传感器故障导致的数据异常对温室环境监测的准确性、环境控制的可靠性都会产生严重危害[6]。因此,在温室环境测控系统的基础上开展多传感器数据融合研究具有重要的经济意义和工程应用价值。
国内外学者已经对传感器数据融合进行了大量研究。常规方法是采用平均值算法简单实现传感器数据融合,该方法适用于具有大量传感器并且应用于对精度要求不高的数据融合中。卡尔曼滤波是应用较多的数据级多传感器数据融合方法,依赖于系统的状态空间模型,而模型的精确程度直接影响数据的融合效果[7-8]。蔡振江等采用基于均值的分批估计法[9]、高峰等使用自适应加权法[10]进行温室数据融合,无需传感器系统的任何先验知识,依靠传感器采集的测量数据即可实现较高精度的融合估计,但若分批估计的传感器分组选择不当将会影响最终的融合效果[11],而自适应加权法对传感器采集结果方差估计所需要的观测误差必须为零均值平稳噪声[12]。针对均值算法融合精度不高的问题,Yager提出一种幂均方算子进行数据融合[13],仅须要计算当前各传感器数据的支持度函数就能获得加权融合的最优权重,无须其他概率统计知识,适用于实时数据融合,但给出的支持度函数在温室无线传感器网络(wireless sensor network,简称WSN)系统中使用时仍存在优化空间。针对高冲突信息融合结果不合理的问题,刘准钆等提出一种基于多源证据融合的加权融合算法[14],该算法根据2个证据的距离大小来确定其相互支持度,将证据支持度矩阵模最大特征值对应的特征向量作为证据的相对折扣因子,并修正证据信息,最后用DS(dempster-shafer)规则进行融合。Lee等提出一种无须模型参数传递的融合方法[15-16],但在温室无线传感器网络中使用时仍有改进空间。
从现场的实际应用出发,针对基于物联网技术的温室环境测控通用系统[17]在运行过程中出现的传感器节点数据异常等情况,本研究提出一种基于时空关联性的温室环境多传感器数据融合方法,该方法以时间相关性和空间相似性预测值为输入变量,基于改进型支持度函数的数据融合算法获得传感器采集点的最优预测值,以提高数据的真实性与可靠性,并利用传感器测量数据进行试验验证。
1 传感器数据融合模型
在温室环境中,时空关联性是指环境参数随着时间和空间变化而变化的规律,可反映环境参数在时间和空间上的关联性,通过研究对象随着空间和时间变化而变化的规律,解决含空间和时间约束的规则发掘问题。研究温室环境时空关联性问题的目的在于发现环境数据的时空关联规则,分析参数的时空变化趋势[18]。
为提高温室环境测控系统多传感器节点采集数据的准确性,本研究通过软件算法来实现传感器节点数据的自修正,设计基于时空关联性的温室环境多传感器数据融合算法(图1),该算法主要包括时间相关性预测、空间相似性估计、多传感器数据融合等。
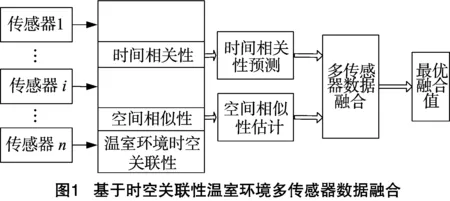
在温室环境测控系统中布置大量各类型的传感器节点,包括同质传感器、异质传感器等,温室内传感器采集的环境参数间具有较强的耦合性,即传感器节点在小气候空间范围内采集的环境参数信息和相邻节点的传感器数据相关或相似。单传感器采集的温室环境数据可构成一个时间序列,通过对时间序列分析发现,在短时间内环境数据之间具有较强的时间相关性。
本研究中基于时空关联性的温室环境多传感器数据融合的主要过程如下:(1)针对温室环境测控系统采集的温室环境数据,基于传感器历史数据,利用基于一阶自回归的时间相关性预测算法获得时间序列预测值,并对不同的时间预测方法进行对比分析。(2)针对温室内各传感器节点采集的温室环境数据之间存在相互关系,相邻传感器节点存在空间相似性的特点,分别利用同质传感器、异质传感器当前时刻数据,建立基于空间相似性的本节点数据预测值,并对不同的空间相似性估计方法进行对比分析。(3)以时空相关性预测结果为输入量,利用本研究提出的基于改进型支持度函数的数据融合算法估计传感器节点数值,获得传感器最优估计值并与基于主成分分析的数据融合方法、平均值法进行预测值与量测值间的比较和分析。
2 基于时空关联性的传感器预测
温室内环境参数一般变化得比较缓慢,传感器真值在较短时间内保持不变,因此可认为,基于时间相关性、空间相似性的时空特性传感器预测值在同时刻服从正态分布。时空关联性包括时间相关性、空间相似性。
2.1 时间相关性预测
时间相关性预测就是利用传感器在温室环境测控过程中环境参数具有时间相关性的特点,采用基于时间特性的预测算法获得下一时刻的预测值。在温室环境测量过程中,传感器节点采集的数据在时间上往往具有一定依存性,即传感器采集的数据可构成时间序列,下一时刻的传感器数据受到现在时刻与历史时刻数据的约束。一般情况下,历史数据对现在和未来数据的影响随着时间间隔的增加而减小。在温室环境的测量过程中,后一时刻的传感器数据主要和前一时刻有关,而受更前一时刻传感器数据的影响较小,可忽略不计,因此认为,温室环境数据具有一阶动态性。本研究结合温室环境的特点,选取一阶自回归预测算法进行温室环境预测。
设温室环境采集的传感器数据构成时间序列xi1,xi2,…,xin,采用一阶自回归时间相关性预测算法[19]进行预测,则第n+1时刻的预测结果为:
(1)
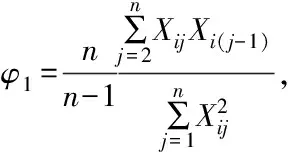
2.2 空间相似性预测
空间相似性估计就是利用相邻传感器间的空间环境分布特性,采用基于空间相似性的预测算法计算出本节点的估计值。在温室环境测控系统中,传感器数据之间存在相互关系,传感器与相邻传感器节点之间存在关联,即传感器之间具有空间相似性。根据空间相似性理论可知,不同传感器在同一时刻采集的温室环境参数之间存在关联性。在测控系统运行过程中发现,相邻的不同或相同类型传感器采集的数据之间存在近线性关系。空间相似性依据对比传感器类型的不同,可被分为同质传感器相似性和异质传感器相似性。根据进行空间相似性预测对象的不同,可以分为同质传感器预测、异质传感器预测。
2.2.1同质传感器相似性预测当利用同种类型的多组传感器同时对观测区域的同一目标进行观测时,同质传感器之间具有很强的线性关系。本研究对传感器节点采集的数据进行相互比较,建立一个基于邻居节点的本节点当前时刻聚合值。
(2)
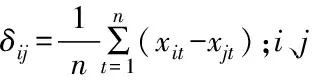
2.2.2异质传感器相似性预测温室的各种环境参数之间存在着耦合关系,通过观察不同传感器采集的不同类型环境参数发现,环境参数之间存在一定的变化规律。在对同一区域进行监测时,不同的监测参数之间存在关联。例如温度与光照度之间具有正相关性,而温度与湿度之间具有负相关性,监测参数之间存在近线性关系。与同质传感器相似性相比,异质传感器能够更好地应用环境及性能的互补作用,扩展空间上的观测范围,增强数据的可靠性。
若具有m+1个相邻监测参数,设m个经过数据预处理的监测参数为自变量,1个目标监测参数为因变量,令自变量表示为:
X={x1n,x2n,…,xmn}。
则回归关系模型可构造形成的矩阵形式为Xm+1=Xmβ+ε,即
式中:β0、β1、β2、…、βm表示线性参数;ε表示随机误差,服从ε~N(0,σ2);X表示回归设计矩阵。
3 传感器时空特性数据融合
数据融合就是将不同传感器的多维信息通过合并和相应的处理得到符合要求的数据结果的整体过程[20]。数据融合在测控系统中常用的方法是平均值法,对被测对象测量值不加区别地计算数据平均值,而忽略不同采集值的权重,适用于大量传感器数据。
本研究采用多种算法模型对传感器信息进行预测,并将各种预测值作为数据融合的输入量,利用提出的基于改进型支持度函数的数据融合算法进行信息融合,并将融合输出量作为最终估计值,该算法能够在保存有效数据的同时剔除冗余数据,为后续的精准控制、故障数据恢复提供数据基础。
同一时刻不同的状态估计值以正态分布形式随机分布,越靠近峰值估计值越多,且估计值之间的支持力度越大;反之,2个估计值之间的数据差越大,两者之间的互相支持度越小。
不同状态预测算法得到的表征数据或不同采集节点待融合数据之间存在关联,其量测方程可以表达为:
xi(t)=s(t)+vi(t),i=1,2,…,n。
(3)
式中:xi(t)表示第i个输入量在t时刻对参数s的量测值;s(t) 表示被测量对象的实测值;vi(t)表示t时刻的量测噪声。
Yager提出采用支持度函数sup(a,b)表示数据b对数据a的支持程度[13],即
(4)
其中,i,j为正整数,i,j=1,2,3,…,n。
文献[21]提出一种常用的支持度函数算法:
(5)
考虑到在温室环境测控系统中多变量、多层次地使用支持度函数会使计算量急剧增加的特点,本研究构造一种改进型支持度函数。
(6)
该改进型支持度函数满足支持度函数的几个条件:(1)sup(a,b)∈[0,1];(2)sup(a,b)=sup(b,a);(3)若|a-b|<|x-y|,则sup(a,b)>sup(x,y),其中,sup(x,y)表示数据y对数据x的支持程度;(4)sup[xi(t),xj(t)]是距离Dij(t)的单调减函数。
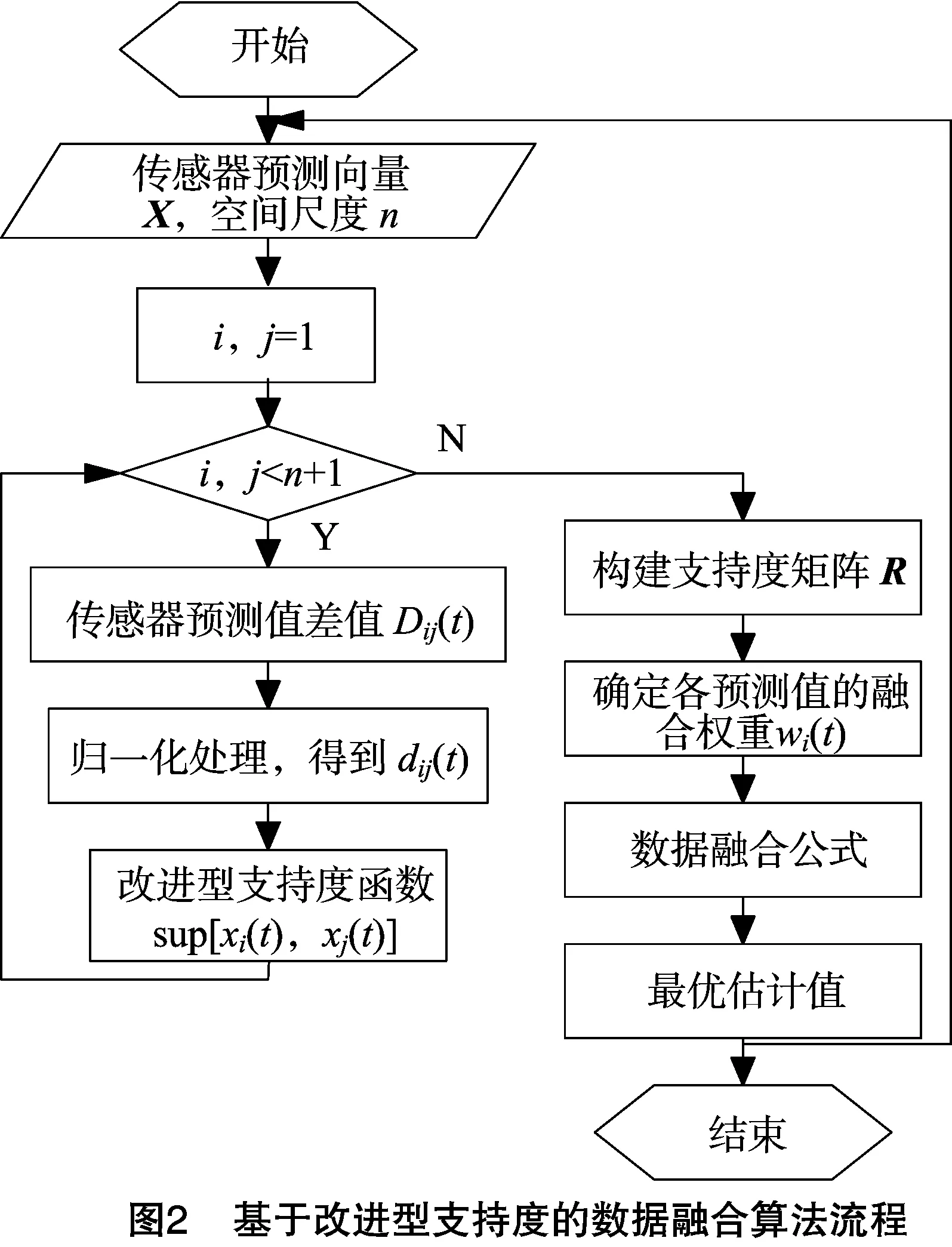
将温室环境数据不同的状态预测值代入改进型支持度函数,建立支持度矩阵函数R,确定第i个测量数据在全体测量数据中的权系数,最终计算出本节点当前时刻异常点的最优估计值。基于改进型支持度函数的数据融合算法流程如图2所示。
4 验证
4.1 试验设备与方法
试验于2015年10月在江苏省农业科学院溧水植物科学基地的温室大棚内进行。通过如图3所示的基于物联网的温室环境测控通用系统采集温室环境数据,系统主要包括协调节点、采集节点、各种类型传感器、智能网关、室外小型气象站和监控软件等。利用各类型传感器节点采集温室内外温度、湿度、光照度、CO2浓度等环境变量。

具体试验方法如下:传感器采集节点每隔1 min读取1次各类型传感器、室外气象站的数据,通过协调节点传输至智能网关,监控软件实现数据的解析、处理、判断、决策、控制等功能。
对多组传感器数据进行分析并仿真,为验证仿真效果,将支持度函数所需的参数设置为K=1、β=0.5,将数据融合、数据预处理中的温度阈值设置为δ=0.5、ε=0.5,对数据预处理、数据融合和数据恢复效果等进行验证,并在不同方法之间作对比分析。
4.2 数据融合效果
数据融合的主要目的是利用传感器节点采集的环境数据计算基于时间相关性的预测值以及同质传感器、异质传感器间基于空间相似性的预测值,并将多种预测方法求得的预测值作为多数据融合的输入变量,利用数据融合算法求得最优估计值。
4.2.1时间相关性验证以基于时间相关性的预测值为期望,以经过数据预处理的传感器节点采集值为准实际值,对数据进行传感器节点时间相关性仿真,时间尺度n=5,则时间相关性数据的验证效果如图4所示。与其他经典的时间序列预测算法[22]进行对比,包括趋势移动平均预测算法、二次曲线趋势时间预测算法,分析结果如表1所示。
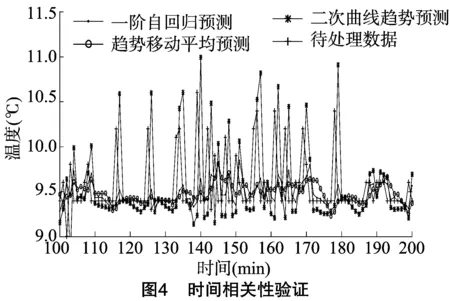
由表1可知,一阶自回归时间相关性预测算法的效果优于其他几种时间预测算法;对数据进行统计发现,99.65%的检测值分布在预测值的阈值区间[r(t)-δ,r(t)+δ]内,传感器数据具有良好的平滑性。

表1 预测算法对比分析
4.2.2空间相似性验证利用传感器节点间的空间相似性,分别验证同节点同质传感器间、同节点异质传感器间以及不同节点同质传感器间的空间相似性,结果如图5所示。
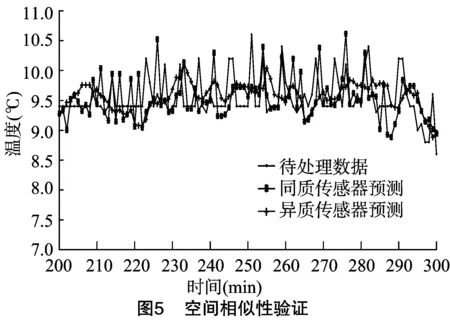
将基于空间相似性的预测值分别与量测值进行对比,得到的数据样本分析结果如表1所示。由表1可知,基于同质传感器的空间相似性预测效果明显好于基于异质传感器的预测算法。
4.2.3数据融合验证将上述基于时间相关性的时间预测值、基于空间相似性的空间预测值作为数据融合算法的输入量进行数据融合,对比支持度函数及其他多种数据融合方式,得到如图6所示的验证结果。其中,平均值算法是一种简单低级的数据融合技术,一种静态加权平均算法;主成分分析算法是一种常用的数据分析方法,通过线性变换将原始数据集用1组与各维度线性无关的数据表示,可用于提取数据的主要特征分量,常用于高维数据的降维。
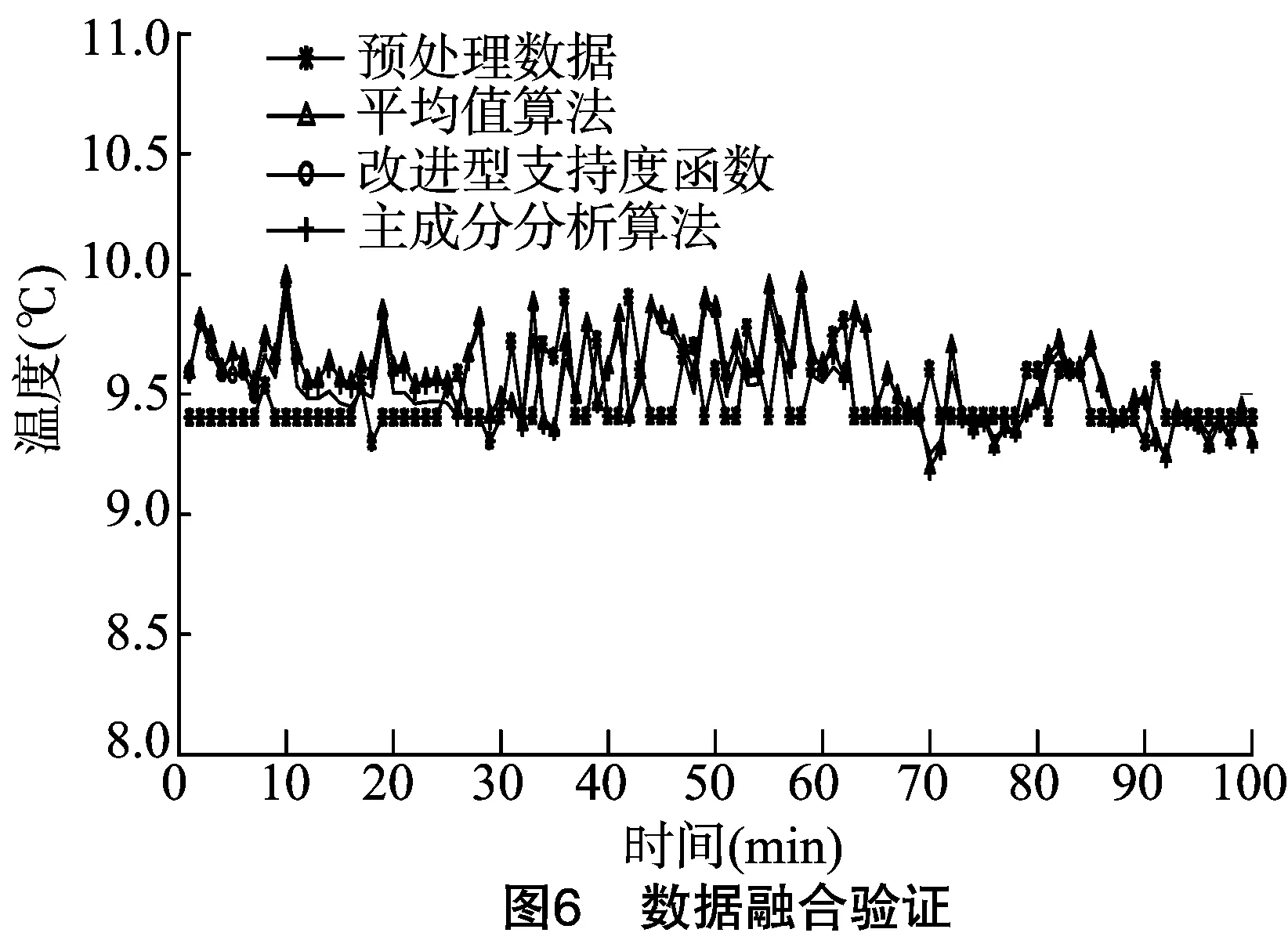
为检验各支持度函数算法、主成分分析算法及传统方法的融合效果,进行多组环境数据验证,结果如表2所示。
由表2可知,平均值法、主成分分析法以及改进型支持度函数的几种算法均能有效地实现数据融合,支持度算法效果优于其他算法,且与其他数据融合算法相比,本研究提出的改进型支持度函数算法表现出较好的性能,融合样本方差较小,验证了本研究提出的改进型支持度函数的有效性。

表2 数据融合结果对比
本研究提出的基于改进型支持度函数的数据融合算法较传统的数据融合算法具有更高的可靠性,能够有效地同时处理多变量之间的支持度,该算法的融合效果优于其他传统数据融合算法。
根据上述内容,本研究选择基于时间相关性的一阶自回归预测算法以及基于空间相似性的同质传感器、异质传感器估计算法,并结合改进型支持度函数数据融合算法对温室环境测控系统的主要环境参数进行组合对比验证。以平均值法、传统支持度函数为对比算法,验证结果如表3所示。
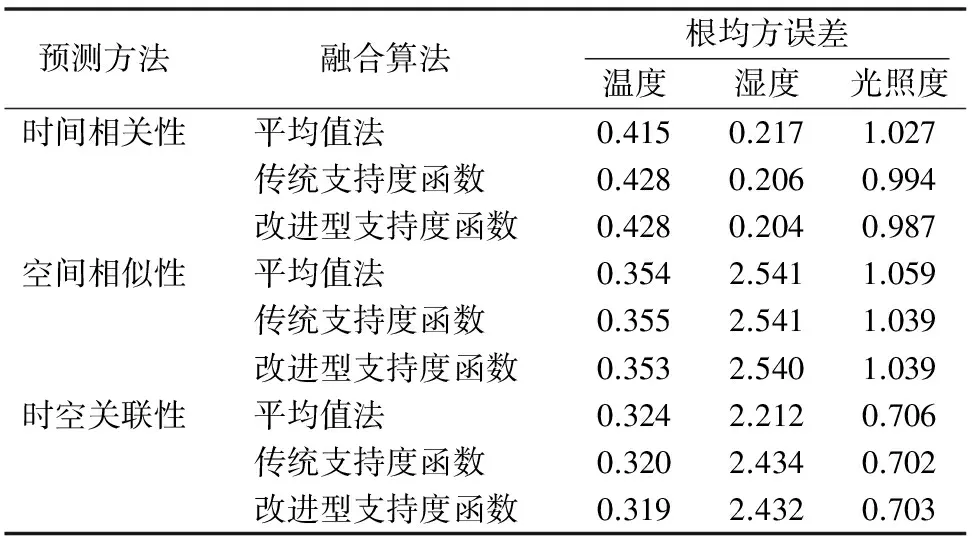
表3 组合对比验证结果
由表3可以看出,基于时空关联性的温室环境数据融合得到的估计结果较基于时间相关性、空间相似性的数据融合要好,基于改进型支持度函数的数据融合效果好于基于平均值法和传统的支持度函数算法。
基于时空关联性和改进型支持度函数的温室环境多传感器数据融合能够更好地反映温室环境参数变化,表现出更好的数据估计效果。
5 结束语
针对温室环境中部分环境参数变化缓慢、冗余度大的特点,对温室环境测控系统中传感器节点采集的温室环境数据进行分析,建立基于时空关联性的温室环境多传感器数据融合算法,实现对温室环境参数的最优估计。
本研究对比不同的时间预测算法对环境数据的时间相关性进行预测和验证,并利用同质、异质传感器的特点对环境参数进行空间相似性预测和验证。对基于时空关联性的预测值分别利用基于主成分分析法和改进型支持度函数算法进行数据融合,并对数据融合的效果进行对比验证。验证结果表明,基于一阶自回归时间相关性预测算法的方差为1.439,优于其他经典时间序列预测算法,同质、异质传感器的空间相似性预测方差分别为1.493、1.883,基于时间相关性、空间相似性的预测算法能够有效地预测节点估计值;对基于时空特性的估计值进行基于改进型支持度函数算法的数据融合,改进型支持度函数融合算法能够有效地赋予时空关联性预测值以动态加权值,且与常用的数据融合算法如平均值算法、传统支持度函数算法等相比,它产生的最优估计值更能真实地反映温室环境的变化,具有可靠性和准确性。
参考文献:
[1]李萍萍,王纪章. 温室环境信息智能化管理研究进展[J]. 农业机械学报,2014,45(4):236-243.
[2]阎晓军,王维瑞,梁建平. 北京市设施农业物联网应用模式构建[J]. 农业工程学报,2012,28(4):149-154.
[3]李莉,李海霞,刘卉. 基于无线传感器网络的温室环境监测系统[J]. 农业机械学报,2009,40(增刊1):228-231.
[4]Díaz S E,Pérez J C,Mateos A C,et al. A novel methodology for the monitoring of the agricultural production process based on wireless sensor networks[J]. Computers and Electronics in Agriculture,2011,76(2):252-265.
[5]张猛,房俊龙,韩雨. 基于ZigBee和Internet的温室群环境远程监控系统设计[J]. 农业工程学报,2013,29(增刊1):171-176.
[6]王海涛,刘倩,陈桂香,等. 粮情监控系统中传感器故障诊断和数据恢复[J]. 中国粮油学报,2013,28(11):86-90,96.
[7]蔡鹤皋,金明河,金峰. 卡尔曼滤波与多传感器数据融合技术[J]. 模式识别与人工智能,2000,13(3):248-253.
[8]李鹏. 卡尔曼滤波在信息融合理论中的应用[D]. 西安:西安电子科技大学,2008.
[9]蔡振江,康健一,张青,等. 数据融合技术在温室温度检测中的应用[J]. 农业机械学报,2006,37(10):101-103.
[10]高峰,俞立,王涌,等. 无线传感器网络作物水分状况监测系统的上位机软件开发[J]. 农业工程学报,2010,26(5):175-181.
[11]张立勇,张利,李丹. 基于最优分组原则的多传感器分组加权融合算法[J]. 仪器仪表学报,2008,29(1):200-205.
[12]翟翌立,戴逸松. 多传感器数据自适应加权融合估计算法的研究[J]. 计量学报,1998,19(1):69-75.
[13]Yager R R. The power average operator[J]. IEEE Transactions on Systems,Man,and Cybernetics,2001,31(6):724-731.
[14]刘准钆,程咏梅,潘泉,等. 证据冲突下自适应融合目标识别算法[J]. 航空学报,2010,31(7):1426-1432.
[15]Lee M H,Choi Y H. Fault detection of wireless sensor networks[J]. Computer Communications,2008,31(14):3469-3475.
[16]季赛,袁慎芳,马廷淮,等. 无线传感器网络中节点故障诊断方法的研究[J]. 计算机工程与应用,2010,46(23):95-97,121.
[17]陈美镇. 基于物联网的温室环境测控通用系统开发[D]. 镇江:江苏大学,2015.
[18]夏英,张俊,王国胤. 时空关联规则挖掘算法及其在ITS中的应用[J]. 计算机科学,2011,38(9):173-176.
[19]回春立,崔莉. 无线传感器网络中基于预测的时域数据融合技术[J]. 计算机工程与应用,2007,43(21):121-125,146.
[20]赵亚光. 基于蚁群算法和BP神经网络的WSN数据融合算法研究[D]. 昆明:云南大学,2013.
[21]段宗涛,程豪,康军. 基于数据融合的多传感器实时数据处理系统[J]. 电子设计工程,2014,22(7):43-46.
[22]索瑞霞,王福林. 组合预测模型在能源消费预测中的应用[J]. 数学的实践与认识,2010,40(18):80-85.
