改进的多项式+周期项模型的卫星钟差预报
2018-04-09廖建发张艳兵
廖建发,张艳兵
(1.海南水文地质工程地质勘察院,海南 海口 571100;2.河海大学 地球科学与工程学院,江苏 南京 211100)
0 引 言
自从20世纪末,美国学者Zumberge提出精密单点定位技术(PPP)以来,GNSS定位技术经历着从双差定位模型到非差定位模型、从模糊度浮点解到整周模糊度固定、从后处理到实时的快速发展历程[1]。影响PPP的实时性的因素主要包括两方面:高精度卫星产品的实时获取和整周模糊的快速固定。因此,如何获取高精度的卫星产品成为实时PPP技术的关键一环。
目前,IGS站提供的IGU产品,其轨道精度实测部分可以达到3 cm,预报部分可以达到5 cm,都可以满足PPP技术的需要,然而其卫星钟差只有在实测部分可以满足PPP技术的要求[2]。因此,国内外学者对如何获取高精度的实时钟差产品进行了众多研究。主要分为两大类:1) 基于定位模型的解析法;分为非差法和历元间差分法。但是这些解析法会引入整周模糊度固定和增大随机误差的影响,不利于钟差产品的实时获取和提高精度;2) 基于实测部分的预报法,常见的钟差预报方法包括多项式模型、灰色系统GM(1,1)模型、和神经网络模型等,并且由这些简单的预报模型衍生出了众多的改进模型[3-10]。熊红伟等提出了基于一次差值的小波神经网络预报模型,通过对在轨卫星钟差求一次差值,实现了卫星钟差1 ns的预报精度[3]。孙大双等提出了顾及周期误差和随机特性的卫星钟差预报方法,通过增加周期项与灰色模型改正,提高了多项式模型的预报精度[4]。陶健春等在灰色GM(1,1)模型的基础上增加了马尔科夫残差修正,有效地提高了短期预报的精度[5]。蔡成林提出了一种超快速星历钟差预报的高精度修正方法,通过对预报数据进行精度修正,提高了钟差预报的稳定性[6]。虽然这些改进方法都在一定程度上优化了常见预报模型,但仍有各自的缺点。
本文基于多项式项+周期项预报模型,提出一种对一次差值进行滑动估计与随机误差迭代修正的钟差预报方法。首先对钟差数据进行一次差分,增加钟差变化的波动特征;然后利用多项式+周期项模型对一次差值做滑动估计;接着根据最小二乘原理对预报值进行随机误差估计分配,重新计算模型系数;最后根据得到的模型系数进行下一步的滑动估计。本文用IGS站提供的采样间隔为15min的钟差产品进行卫星钟差预报,通过对比不同预报方法,验证了本文方法的有效性。
联系人: 张艳兵E-mail: 1821708477@qq.com
1 改进的多项式+周期项模型
1.1 多项式+周期项模型
事物变化主要包括趋势变化、周期变化以及随机变化,因此,卫星钟差的变化模型可以假设为趋势变化、周期变化和随机变化的组合变化,趋势变化可以用多项式进行表示,周期变化可以用具有周期性的三角函数进行表示,即:
(1)
式中: ∂Ti为历元时刻ti的卫星钟差; a0、a1和a2分别为多项式的二阶系数; A、ω和φ0分别为周期项的振幅、角速度和初相; ε为卫星钟差的随机误差。
以IGS站PG01卫星2017-11-11的15 min采样间隔的精密钟差数据为例,分析卫星钟差原数据和一次差值随观测历元的变化,结果如图1和图2所示。从图1中可以看出:由于历元间卫星钟差原数据变化量相对于原数据很小,导致卫星钟差原数据对卫星钟差的波动变化反映不够明显;而图2中的一次差值通过相邻历元间做差,降低了实验数据的量级,有利于卫星钟差模型的分析与预报。
为此,在相邻历元间对卫星钟差进行做差,即:
ΔTi=∂Ti+1-∂Ti
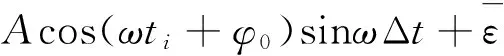
(2)
1.2 随机误差的修正
针对随机误差的修正,可以通过对拟合残差序列的分析,来估计预报值的残差序列,但是这种做法使随机误差失去了其特有的随机特性,且随着预报时间的增长,其累积的误差也越来越大,降低了卫星钟差预报的稳定性。因此,本文提出一种基于迭代法的随机误差自然修正法,主要分为以下几个步骤:
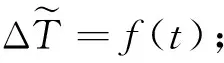
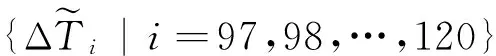
2 算例分析
本文采用IGS站提供的2017年11月11日到13日的PG01卫星的精密钟差产品IGU和IGS,首先用11日的IGU数据预报12日和13日的卫星钟差数据,然后将预报的卫星钟差数据与IGS数据进行对比。为了验证本文算法的优越性与稳定性,采用以下方案对12日的卫星钟差进行预报:方案一:采用多项式模型对IGU原数据与一次差数据进行短期预报;方案二:采用灰色GM(1,1)模型对IGU原数据与一次差数据进行短期预报;方案三:采用多项式+周期项模型对IGU原数据与一次差数据进行短期预报;方案四:采用改进的多项式+周期项模型对IGU原数据与一次差数据进行短期预报,预报结果如图3和表1所示。
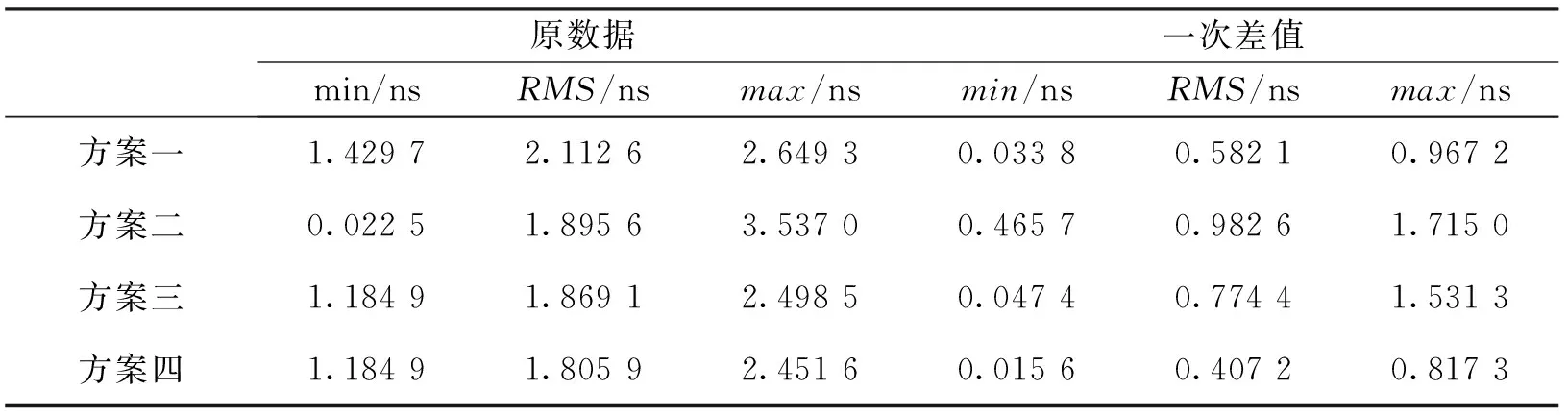
表1 4种模型一天预报结果精度分析
从图3中可以看到:多项式模型、多项式+周期项模型和改进的多项式+周期项模型对一次差值进行钟差预报的结果要优于对原数据的钟差预报结果;在开始的40个历元内,原数据的灰色系统预报值要优于一次差值的预报结果,但在一天的预报时间里,一次差值的灰色系统预报值比原数据的预报值更加稳定。从表1可以看出:对于采用原数据或一次差值进行卫星钟差预报,改进的多项式+周期项模型RMS最小;对于一次差值,方案四预报的钟差值偏离真实值的最大程度也最小,最大值为0.82 ns.
从图4和图5中可以看到:针对原数据,4种模型的钟差预报结果都要低于IGU的预报精度;针对一次差值1天的卫星钟差预报,灰色GM(1,1)模型、多项式+周期项模型与IGU的预报精度相差不大,而多项式模型与改正的多项式+周期项模型的预报精度明显优于IGU的预报精度;针对一次差值2天的卫星钟差预报,多项式模型、灰色GM(1,1)模型、多项式+周期项模型都出现了明显的趋势性预报,预报精度迅速降低,而改正的多项式+周期项模型预报值仍能达到1.47 ns的精度。这些结果证明了改正的多项式+周期项模型在1天内的短期预报中可以实现高精度预报,并且改正的多项式+周期项模型在多天的长期预报中稳定性比其它几种模型更高。
3 结束语
本文将多项式+周期项拟合模型和随机误差自然修正相结合进行卫星钟差预报。通过算例分析表明了:1) 相比原数据,一次差值更能准确反映卫星钟差的变化规律,便于卫星钟差通过某一模型近似表达;2) 多项式模型、改正多项式+周期项模型通过对一次差值的估计,可以在一天的钟差预报中达到1 ns的预报精度;3) 针对一次差值,多项式模型和多项式+周期项模型在10小时后的预报精度大幅降低,而针对原数据,两者的预报精度都比较稳定,没有出现预报精度大幅降低的现象,说明一次差值预报更容易受到预报模型趋势项误差的影响;4) 多项式+周期项模型在10小时内的预报精度优于多项式模型,说明了在多项式拟合函数上增加周期项,更符合卫星钟差的变化规律;5) 尽管改进的多项式+周期项模型在最初10 h内的预报精度略微低于多项式+周期项模型,但其通过滑动估计与实时随机误差修正模型,降低了趋势项与随机误差对卫星钟差预报精度的影响,实现了1天内RMS为0.41 ns的卫星钟差预报。
[1]张小红,李星星,李盼. GNSS精密单点定位技术及应用进展[J]. 测绘学报,2017,46(10):1399-1407.
[2]李征航,黄劲松. GPS测量与数据处理[M]. 武汉:武汉大学出版社, 2016.
[3]熊红伟,程新文,张海涛,等. 卫星钟差单差的小波神网络预报[J]. 测绘科学,2017,42(9):9-14,48.
[4]孙大双,吕志平,王宇谱,等. 一种顾及钟差周期误差和随机特性的卫星钟差预报方法[J]. 大地测量与地球动力学,2016,36(12):1078-1082.
[5]陶健春,王秉钧. 改进的灰色GM(1,1)在北斗卫星钟差短期预报中的应用[J]. 工程勘察,2017,45(4):55-59.
[6]蔡成林,何成文,韦照川. 一种GPS IIR-M型卫星超快星历钟差预报的高精度修正方法[J]. 测绘学报,2016,45(7):782-788.
[7]蔡成林,于洪刚,韦照川,等. 基于Takagi-Sugeno模糊神经网络模型的卫星钟差预报方法[J]. 天文学报,2017,58(3):113-126.
[8]王宇谱,吕志平,周海涛,等. 基于修正钟差一次差分数据的卫星钟差预报[J]. 大地测量与地球动力学,2016,36(12):1073-1077.
[9]王利,张勤,黄观文,等. 基于指数平滑法的GPS卫星钟差预报[J]. 武汉大学学报(信息科学版),2017,42(7):995-1001.
[10]程瑞江,陈西宏,刘赞,等. 一种遗传算法优化的卫星钟差预报[J]. 测绘科学,2017,42(5):25-28,34.
