自适应磷虾群优化Elman神经网络的目标威胁评估

李志鹏，李卫忠，杜瑞超

LI Zhipeng,LI Weizhong,DU Ruichao

空军工程大学 防空反导学院，西安 710051

Air and Missile Defense College ofAir Force Engineering University,Xi’an 710051,China

1　引言

目标威胁评估（Target Threat Assessment）是现代作战决策的基础，及时准确地对敌方目标威胁做出评判，为军事决策提供信息支持，是提高作战制胜能力的关键[1-2]。目前，用于目标威胁评估的方法主要有：云模型[3]、贝叶斯网络[4-5]、多属性决策法[6-7]、直觉模糊集[8]、TOPSIS[9]、DS证据理论[10]以及支持向量机[11]等。这些方法各有特点，但其参数的确定多依赖于专家经验，难以对作战环境变化所引起的复杂关系做出灵活反映。文献[12-13]分别将BP神经网络用于无人机航迹规划气象威胁度模型和威胁度估计，为威胁评估问题提供了一种简单实用的解题思路，但其实时适应性较弱。Elman动态神经网络在BP网络的基础上引入储存记忆环节，具有非线性、并行性、适应时变、自学习等特点，同时训练速度和稳定性有所改善，可以较好反映动态过程系统的特性[14]，适用于建立不确定问题的预测模型，但其仍存在易陷入局部极值等缺陷，因此考虑用其他算法对Elman网络进行优化。

鉴于磷虾群（Krill Herd，KH）算法[15]易于实现且具有良好的寻优性能，本文对其进行改进，提出一种自适应磷虾群（Adaptive Krill Herd algorithm，AKH）算法，用于Elman神经网络初始参数的搜索，建立了自适应磷虾群优化Elman神经网络（Elman neural network optimized by AKH，AKH-Elman），并应用于目标威胁评估，在保证一定收敛速度的基础上，使寻优精度得到显著提升。

2　自适应磷虾群算法

2.1　基本磷虾群算法原理

磷虾群算法（KH）是一种模拟磷虾群觅食行为的启发式优化算法，它通过磷虾之间的食物感应和信息交换，对个体位置不断迭代更新，直至达到终止条件，输出最优解。每个磷虾个体代表n维解空间内的一个潜在解，从而将最优化问题转化为在一个解空间内的全局搜索问题。

在KH算法中，可以将磷虾个体的移动分为三个主要部分，其第k次的移动可表示为：

基于最近邻感应原则，若磷虾个体与其他个体之间的距离小于所设定的感知半径，则向距离最近的磷虾方向移动。磷虾i受其他磷虾影响下的第k次引导移动可表示为：

随着算法的迭代运行，磷虾群的位置逐渐向最优解靠近，在此过程中，引导移动和觅食移动对个体活动的影响不断减小，随机扩散活动随之减弱。因此，考虑在表达式中加入迭代递减的环节：

其中，K为最大迭代次数。

2.2　磷虾群算法改进

启发式优化算法的优化作用主要体现全局探索能力和深度寻优能力。全局搜索即避免算法陷入局部最优，确保在有限时间内寻找到全局最优解；深度寻优则指在当前最优解附近的局部范围内继续探寻更优解的过程。算法须对两者兼顾，才能发挥较好的优化性能。本文提出一种自适应磷虾群算法，将进化算法中的遗传繁殖机制引入到KH算法，并加入两个基本算子构成自适应环节。

2.2.1遗传机制

群优化算法常存在样本退化的缺点，为克服这一问题并改善种群多样性，在KH算法中引入遗传繁殖机制，加入交叉、变异操作，以提高算法性能。

（1）交叉操作模拟基因重组过程，按一定的交叉概率Pc对种群中两个个体的部分基因替换重组，这在很大程度上提高了算法的全局搜索能力。定义个体i和 j通过变异操作产生新个体的过程为：

（2）变异操作以变异概率Pm对个体进行修改，防止算法出现早熟，其定义为：

Pc和Pm的选取非常重要，其值过小会导致过早收敛；过大则会影响优良基因。本文采用一种自适应的方法对其进行调整[16]：若个体趋于局部最优或适应度相似，两概率值应适度增大；若个体差异较大，分布较分散，应适当减小Pc和Pm。

种群收敛度用种群平均适应度和最优个体适应度的差值反映：

同时，由于种群个体的差异性，对不同个体其Pc和Pm也应不同：适应度值越低，其Pc和Pm应越小，适应度值越大，其Pc和Pm应越大，因此按下式计算：

2.2.2自适应调节

为提高磷虾群算法的搜索和寻优性能，本文通过引入两个基本算子——进化算子α和优化算子β，为KH算法增加一个自适应环节。

（1）进化算子α

进化算子α模拟“优胜劣汰”法则，能使算法的收敛速度得到提高。在生态环境相对稳定的条件下，生物种群规模通常保持在一定规模，在繁衍过程中，劣势个体被淘汰，失去种群延续的资格，而优良个体能顺利存活并繁殖出下一代，所以种群中优良个体的数目逐渐增加。算子α从规模为M的种群中选取部分优良个体赋予繁殖权限，以强化算法的寻优能力。

为减小复杂程度，α是以适应度值的大小为度量标准，对当前个体从优到劣按序排列，选取前Q个最优个体繁殖出新个体。在一次迭代中，Q个可繁殖个体生成Q个新个体，为保持种群规模不变，用新个体替换同样数目的最劣个体，如式（12）：

p为可繁殖个体所占比例，决定了种群中可繁殖个体的数量Q，其设置不宜过大，否则会因种群基因过度改变致使算法适用性下降，本文取 p=0.2；为可繁殖个体i的位置，其繁殖出的新个体位置为；R是指个体距当前最优解的最近距离；取[-0.3,0.3]的成了最劣个体的替换。

（2）优化算子β

KH算法中，最优个体位置是影响种群位置更新的决定因素，距最优磷虾越近的个体，其位置更新将会受到越大限制，这是影响算法寻优精度的主要因素之一。为提高算法在最优解附近搜寻潜在更优解的能力，加入优化算子β，具体操作如下式。是种群个体与最优磷虾的最远距离，赋权值ξ＞0以调节邻域范围的限定，根据实际应用效果，本文取ξ=0.1。算子β只针对最优解邻域的个体，为其增加一个随机位移量Γ，为 [-0.3,0.3]上的随机值。这就使最优解附近的个体突破局部限制，搜索附近更优解。β增强了算法搜索最优解的能力，寻优精度得到提高。

3　基于AKH优化Elman神经网络的目标威胁评估

3.1　威胁评估因素及数据预处理

对于复杂性问题，考虑的因素越多，得到的结果通常会越精确，但也会使过程变得复杂，因此建立目标威胁评估模型，应根据与目标威胁度的相关程度对参数作出合理取舍。本文结合经验，筛选出目标类型、距离、高度、速度、航向角及干扰能力等6个主要因素作为威胁评估的依据。此外，需要对原始样本数据进行预处理，通过数据量化和归一化等操作，使数据能被模型直接识别。

（1）目标按类型分为大型目标、小型目标和直升机，将三者依次量化为0.6、0.8、0.2。

（2）目标速度越大，突破防御的可能性越高，威胁度越大，构造隶属度函数：

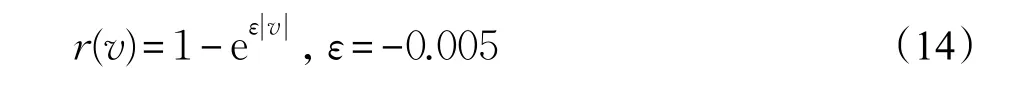
（3）目标高度越低，则其被发现的概率越小，威胁度越大，隶属度函数为：

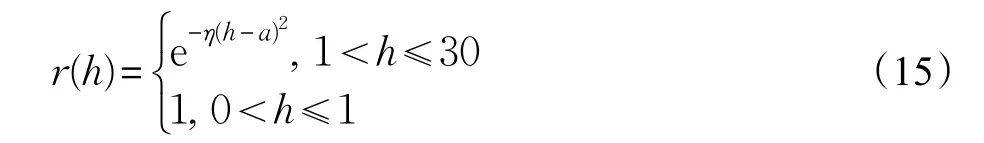
其中，η=0.005 km-2，a=1 km。

（4）敌我距越小，攻击意图越明显，威胁越大，隶属度函数为：

（5）目标航向角越小，威胁越大，从0°至36°等间隔量化为0.9～0.1。

（6）干扰能力可分为强、中、弱、无4个等级，依次量化为0.8、0.6、0.4、0.1。

3.2　AKH-Elman目标威胁评估模型

3.2.1Elman神经网络

Elman神经网络是一种动态递归神经网络，主要包括前馈连接和反馈连接两部分[17]。它在前向神经网络的基础上，引入反馈信号，增加了一个相当于延时算子的承接层，使系统具有了适应时变性，其结构如图1所示。

图1　Elman网络结构图

图1反映了各层节点之间的关系，ω1、ω2、ω3分别表示输入层到隐层、承接层到输出层和隐层到输出层的连接权值，其值可以修正，而递归部分的权值是固定的。Elman神经网络的数学模型可表示为：

Elman网络通过反馈增强了动态信息处理能力，预测性能比BP神经网络更优越，但其连接权值采用梯度下降法完成更新，学习速度较慢，且易陷入局部极值等。

3.2.2建立AKH优化Elman网络的威胁评估模型

（1）初始化种群

由于算法的运算对象是问题解集的编码，因此，需要采取合理的方式对变量编码。常用的编码方法有：二进制编码、浮点数编码、乱序编码等[18]。本文采取实数编码，由输入层和隐含层之间的连接权值、隐含层阈值、隐含层与承接层之间的连接权值、隐含层和输出层之间的连接权值以及输出层阈值组成一个实数串，每个实数串即代表一个个体。按照选取的影响威胁评估的6个因素，本文构建的AKH-Elman神经网络在输入层包含6个节点，对应有6个输入参数，输出层包含1个节点，对应有1个输出参数，中间层的节点数主要依据经验公式与实验验证，取隐含层和承接层节点为11个，对应有权值个数6×11+11×11+11×1=198个，阈值个数11+1=12个。

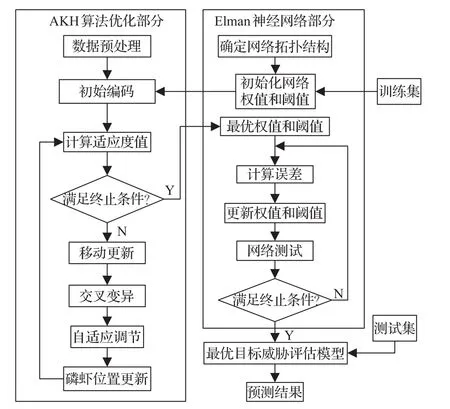
图2　AKH-Elman算法流程

（2）适应度函数

由最优个体编码，可以确定Elman网络的初始参数，从而构造出Elman网络结构，然后利用训练集对其进行训练。通过训练后的系统可以完成对目标威胁值的预测，根据Elman预测与期望之间的差值来确定适应度函数，即：

（3）更新操作

算法在每次迭代更新过程中，将根据式（19）所定义的适应度函数，计算出每个个体的适应度，并完成个体位置的更新。更新过程按照引导移动、觅食移动和随机扩散三部分展开，分别对应于式（2）、式（3）和式（6）；最后对引导移动、觅食移动、随即扩散的结果加以综合，并经过交叉、变异和自适应调整环节，完成磷虾个体位置的更新。

更新操作完成后，则重新对个体适应度值进行计算，并反复进行以上所述的迭代操作，用适应度好的个体替代适应度差的个体，直至满足终止条件或达到最大迭代次数，得到优化的Elman神经网络初始参数。

（4）网络训练

“别老拿着匕首在我眼前晃。”一杭说。范坚强笑了，“怎么，怕了？只要你交出从公厕看守那里找到的记事本，我可以考虑饶你一命。”

学习和训练Elman网络，对其权值和阈值进行更新，直到收敛。

（5）目标威胁评估

网络训练收敛后，就确定了目标威胁评估模型，将测试集中的数据输入，以完成对目标威胁值的预测。

4　仿真实验与结果分析

4.1　实验设计

仿真实验原始数据从某系统的目标威胁数据库中随机获取，按目标类型分别选取大型目标、小型目标和直升机数据各200组作为训练集，另外选取18组数据组成测试集。测试集数据见表1。

表1　测试集数据

在 Intel®Core™ i7-4790 CPU@3.60 GHz计算机平台上，利用64位Windows 7操作系统中的MATLAB 2012b软件编程实现AKH-Elman目标威胁评估。实验参数设置：种群规模M=40，最大引导速度Nmax=0.02，最大扩散速度Dmax=0.006，K=100。分别利用训练集对传统Elman网络、基本磷虾群优化Elman网络和AKHElman网络进行训练，并对测试集中的目标威胁度进行评估，将得到的目标威胁预测值与实际威胁度进行比较。

4.2　仿真结果

对Elman网络、KH-Elman网络和AKH-Elman通过训练集训练后，分别用于对测试集中目标威胁度的预测评估，并将实验结果进行比较。图3对3种方法所得的目标威胁评估值与实际值进行了比较，图4更直观地反映出评估误差。

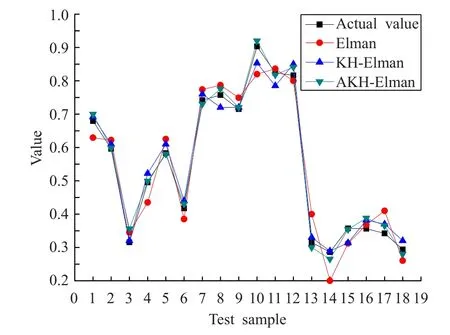
图3　目标威胁评估值与实际值的比较

图4　目标威胁评估误差比较

从测试结果看，AKH-Elman网络的预测精度最高，除对样本3的评估误差较大外，其余样本处误差较小；而Elman网络的预测效果最差。相比KH-Elman网络，除样本1、3、14外，AKH-Elman对其他样本的评估都得到了优化。总体上看，3种方法的预测精度从高到低依次为：AKH-Elman＞KH-Elman＞Elman。

从图5也可以看出，与KH算法相比，AKH算法优化Elman神经网络在迭代收敛速度上相差不大，但最终的运行结果得到明显改善，说明本文所提出的自适应磷虾群算法在应用中是有效的。

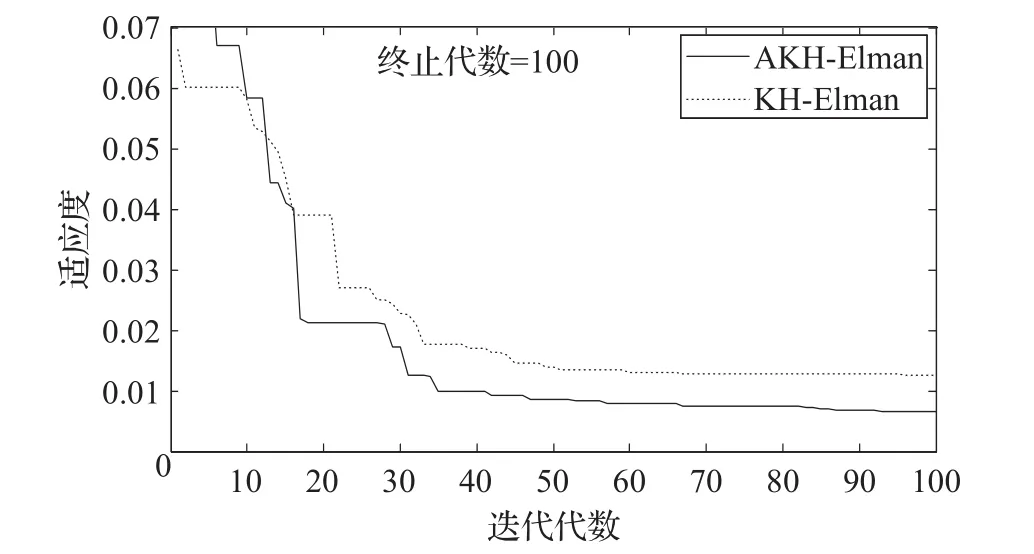
图5　迭代优化曲线图

从表2看出，Elman、KH-Elman和AKH-Elman的平均预测时间分别为：3.09 s、4.26 s、4.20 s，AKH-Elman和KH-Elman相比传统Elman预测时间耗费略长，但差别不大且都在系统允许范围之内，满足通常状况下的目标威胁评估要求。

表2　评估时间和平均误差

5　结束语

本文对磷虾群算法进行了改进，加入遗传机制和自适应环节，提出一种AKH算法，并将其用于Elman神经网络的优化，通过AKH算法对Elman神经网络的初始权值和阈值进行寻优，并以此为基础建立起目标威胁评估模型。通过对目标威胁测试集的仿真实验，验证了AKH算法对Elman神经网络的优化效果，算法既保证了一定的收敛速度，又能够使寻优精度得到明显提升，提高了模型预测的准确性，相较于传统Elman神经网络和KH-Elman网络具有明显的优越性。而对算法时间效率的改进是后续研究的重点。

参考文献:

[1]Looney C G，Liang L R.Cognitive situation and threat assessments of ground battle spaces[J].Information Fusion，2003，4（4）：297-308.

[2]黄璇.多源引导信息融合及其关键技术研究[D].北京：中国科学院大学，2016.

[3]Wang X，Yu Y.Efficiency evaluation of commandinformation system based on cloud model[C]//Proceedings of International Conference on Intelligent Human-machine Systems and Cybernetics，2014：148-151.

[4]Jannson T，Forrester T，Wang W，et al.Bayesian truthing as experimental verification of C4ISR sensors[J].Proceedings of SPIE，2015，9456：1-12.

[5]刘海燕，陈红林，史志富，等.基于模糊贝叶斯网络的空中目标多传感器融合识别研究[J].电光与控制，2009，16（3）：37-41.

[6]Rogova G L.Adaptive real-time threat assessment under uncertainty and conflict[C]//Proceedings of IEEE International Inter-Disciplinary Conference on Cognitive Methods in Situation Awareness and Decision Support，2014：59-65.

[7]Unver S，Gurbuz T.Threat evaluation using analytic network process[J].IFAC Papers on Line，2015，48（3）：8-13.

[8]雷英杰，王宝树，路艳丽.基于自适应直觉模糊推理的威胁评估方法[J].电子与信息学报，2007，29（12）：2805-2809.

[9]范学渊，邢清华，黄沛，等.基于TOPSIS的战区高层反导威胁评估[J].现代防御技术，2012，40（4）：108-112.

[10]宋亚飞，王晓丹，雷蕾，等.基于证据理论和混淆矩阵的传感器可靠性评估[J].控制与决策，2015（6）：1111-1115.

[11]Wu L Y，Sun Y Q，Ji J Y.Study on threat assessment based on rough ret and support vector machines for regression in BVR air combat[J].Applied Mechanics and Materials，2013，419：228-234.

[12]朱国涛，周树道，叶松，等.基于Elman神经网络的气象威胁度建模和评估方法研究[J].电光与控制，2011，18（3）：69-71.

[13]马海涛.基于神经网络和遗传算法的威胁度估计算法[J].军事运筹与系统工程，2005，19（3）：71-74.

[14]Li X，Chen Z Q，Yuan Z Z，et al.Generating chaos by an Elman network[J].IEEE Transactions on Circuits and Systems-I：Fundamental Theory and Applications，2001，48（9）：1126-1131.

[15]Gandomi A H，Alavi A H.Krill herd：A new bio-inspired optimization algorithm[J].Commun Nonlinear Sci Numer Simul，2012，17（12）：4831-4845.

[16]谭宝成，廉春原，徐艾，等.一种基于改进遗传算法的机器人路径规划方法[J].西安工业大学学报，2008，28（5）：456-459.

[17]Yi-Hui L.Evolutionary neural network modeling for forecasting the field failure data of repairable systems[J].Expert Systems with Applications，2007，33（4）：1090-1096.

[18]Lv R L，Guan X M，Li X Y，et al.A large-scale flight multi-objective assignment approach based on multiisland parallel evolution algorithm with cooperative coevolutionary[J].Sci China Inf Sci，2016，59（7）：072201.