基于数学规划法的105团农机配备研究

周 雪，赵永满，王向阳

（石河子大学机械电气工程学院，新疆 石河子832000）

0　引言

农业机械（简称农机）配备是农业机械化（简称农机化）管理的重要环节，农机配备合理与否，关系到机械化能否取得良好的经济效益，加强农机配备研究，可达到使用最少投入、获得最大经济效益的目标[1]。农机配备的计算方法有很多，随着系统工程理论逐渐渗透于农机领域，目前借助计算机对农机配备进行模拟的数学规划模型已发展的较为成熟。该模型综合考虑了全年各个时期的作业时间、作业量、适时性损失、机械生产率等因素，考虑问题较全面，是一种行之有效的农机配备方法。

近年来，国内外应用数学规划模型进行农机配备的研究已有较多，例如：Audsley根据农场相关数据信息，应用数学规划模型，输出最佳种植下的农机使用量，结果表明：该模型可解决管理、生产等领域的农机配备问题，帮助农场计划农作物的耕种、劳动量和机械量，然而该方法忽略了天气因素[2]；Whitson等在考虑天气条件情况下，运用数学规划法对德克萨斯州高粱、棉花、豆类、玉米等作物生产所需农机系统进行配备[3]；Bender等也应用数学规划模型对德克萨斯州进行农机配备相关研究[4]；张宏文[5]、程敬春[6]、张威[7]、李鑫尧[8]、董升涛[9]等都采用数学规划法建立以最小成本为目标函数、作业量和作业机时为约束条件的农机配备模型，并运用该模型对不同地区的农机进行配备，证明了该模型的实用性和可行性。

新疆生产建设兵团（简称兵团）的农业发展迅速，机械化水平不断提高，截至2016年末，兵团农机总动力已达到519.38万kW，拥有大中型拖拉机49 791台，大中型拖拉机配套农具81 911台（架）[10]。而兵团第六师105团（简称105团）农机总动力已达到43 700 kW，拥有大中型拖拉机714台，大中型拖拉机配套农具1143台（架），农机具配套比为1:1.6，由此可知：105团农机化发展水平较好。然而，由于兵团农机的总体结构和区域发展不平衡，农机发展体制不完善，兵团仅凭借经验进行农机的购置，一味地追求农机的数量和性能，缺乏科学的农机配备方案[11]。105团的农机系统就存在着农机配备不当的问题，有必要运用数学规划模型对105团的农机配备进行研究，完善105团农机配备方案，这对减轻农民负担、降低农机作业成本以及提高农机利用率具有重要意义，以期为105团农机工作人员对种植规模和农机配备方案的进一步研究提供有力的支持。

1　105团农机配备模型的构建

1.1　线性规划法

1.1.1设变量

线性规划模型的变量类型主要包括各种农机配备数变量和农机进行各项作业的机组台班数变量。

1.1.2建立约束方程

由于105团属于温带大陆性气候，全年干旱少雨，农机具下地作业受到雨水的影响较少，所以本文中完成各项作业的农机具可下地时间概率均取0.9。

（1）作业量约束

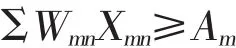
式中 Xmn—第n种作业机组进行第m项作业的台班数量，单位：台班；Wmn—第n种作业机组进行第m项作业的台班生产率，单位：亩/台班；Am—第m项作业需要完成的作业面积，单位：亩。

（2）拖拉机配备量约束

式中 Xim—第i种拖拉机完成第m项作业所用的台班数量，单位：台班；Tm—第m项作业阶段拖拉机的可下地时间概率；Mim—第i种拖拉机完成第m项作业的最大作业班次，单位：台班；Xi—第i种拖拉机的配备量，单位：台。

（3）农具配备量约束

式中 Tm—第m项作业阶段农具的可下地时间概率；Xjm—第j型农具完成第m项作业所用的台班数量，单位：台班；Xj—农具配备量，单位：台；Mm—第m项作业的最大可作业班次数，单位：台班。

（4）变量非负约束

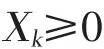
式中 k—变量序号；Xk—所设变量。

1.1.3建立目标函数

本文以作业成本最小为目标，构建目标函数模型，即：

式中 C固—全年农业机械作业固定费用；C变—全年农业机械作业可变费用。

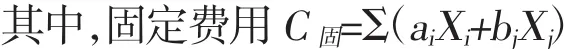
式中 i—拖拉机序号；j—农具序号；ai—第i种拖拉机全年作业的固定费用，单位：元/台；Xi—第i种拖拉机全年的配备数量，单位：台；bj—第j种农具全年作业的固定费用，单位：元/台；Xj—第j种农具全年的配备数量，单位：台。

式中 m—作业序号；n—完成第项作业相关的机组；Cmn—第n种作业机组进行第m项作业的可变费用，单位：元/亩；Wmn—第n种作业机组进行第m项作业的生产率，单位：亩/台班；Xmn—第n种作业机组进行第m项作业的台班数量，单位：台班。

1.1.4软件求解

本文构建的模型变量较多，需应用软件进行求解。Lingo（Linear Interactive and General Optimizer）是一种交互式的线性通用优化求解器，可以求解线性和非线性优化问题，功能强大，执行速度快，使用简便灵活[11]。

1.2　工作量法

当完成某项作业需要其特定的农机并且与其他作业没有关联时，比如收获机械，采用工作量法建立配备模型较为简便，其模型如下：

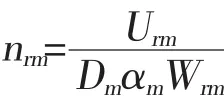
式中 r—农机序号（文中主要指收获机械）；nrm—完成第m项作业需要r型农机的数量，单位：台；Urm—r型农机需要完成的第m项作业的面积，单位：亩；Dm—第m项作业实际可作业天数，单位：天；αm—第m项作业每天的可作业班次数，单位：台班；Wrm—r型农机完成第m项作业每班次的生产率。

2　105团不同种植规模的选择与配备分析

2016年，105团的耕地面积为 8 186.7 hm2，其中 4 289.3 hm2棉花，1 333.3 hm2小麦，666.7 hm2番茄。根据当地的种植要求和特点，经调研，可获得以下数据信息：105团主要农作物的全年机械化作业工艺流程见表1；105团农机具的固定费用见表2；105团的机组可变费用见表3。

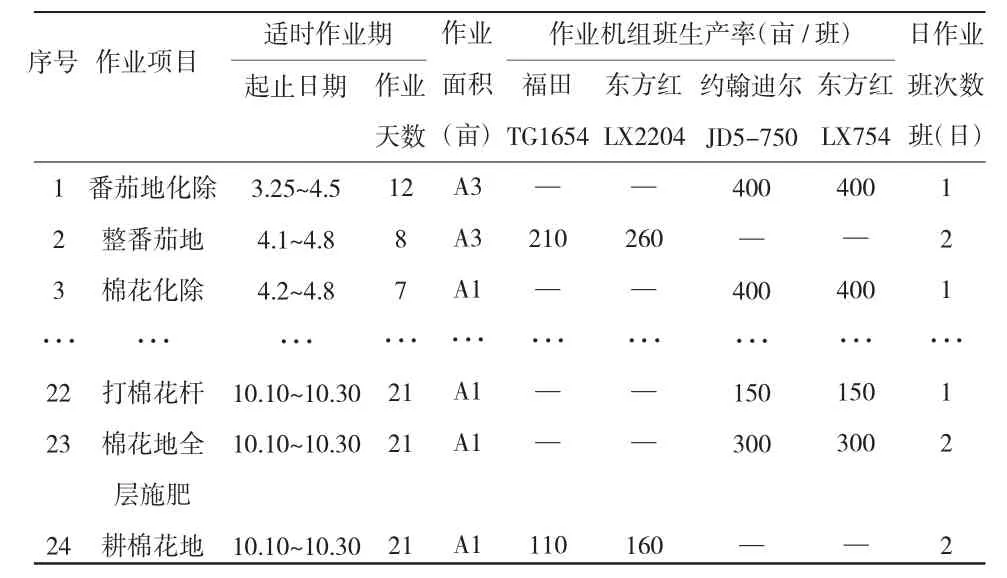
表1　105团主要农作物的全年机械化作业工艺流程表

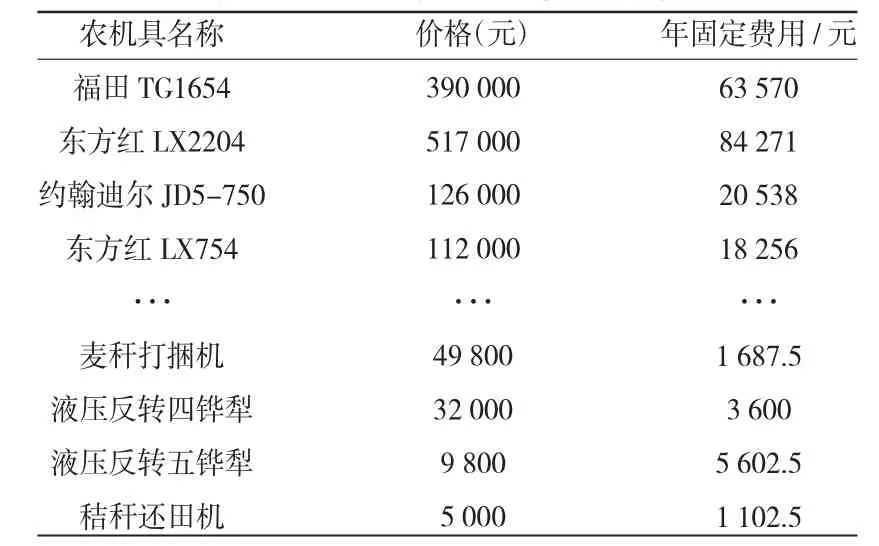
表2　105团农机具的固定费用

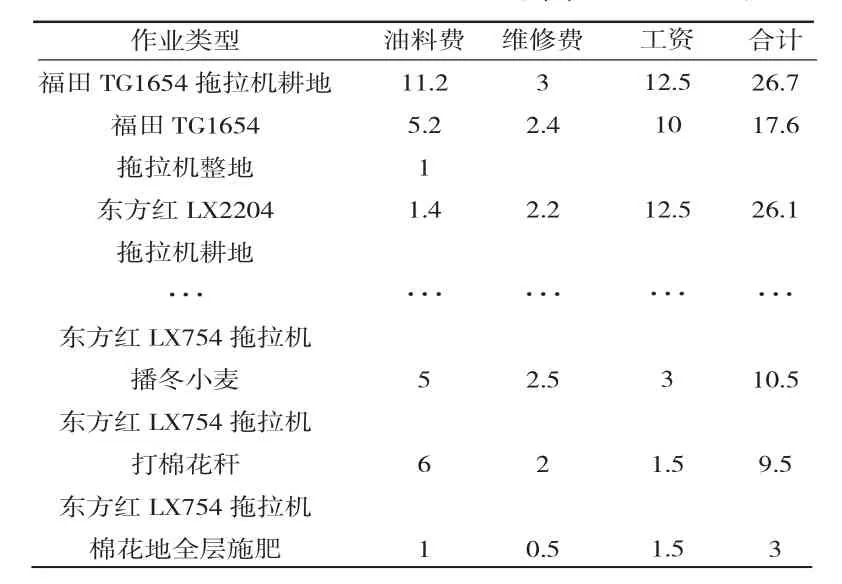
表3　105团的机组可变费用（单位：元/667m2）

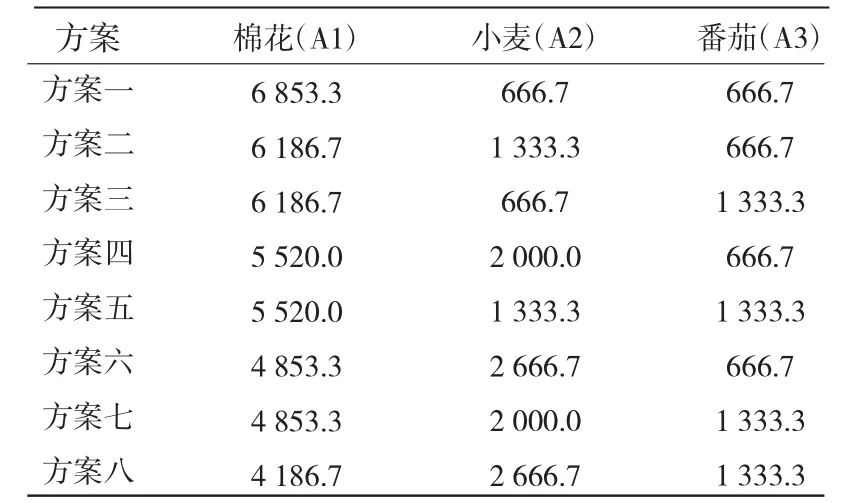
表4　种植规模的具体情况（面积：hm2）

由于棉花为105团主要农作物，小麦、番茄种植面积过多会造成收获机械供不应求，势必增加作业成本，从而选取8种105团不同的种植规模情况，见表4。

利用第1节所述方法对各种植规模建立农机配备模型，配备过程在此不再赘述，每种种植规模可得到1种农机配备方案，应用软件完成对105团多种农机配备方案的对比分析，见图1、图2、图3，各种植规模配备方案的全年机械作业成本见表5。

表5　各种植规模配备方案的全年机械作业成本（单位：万元）

由表5可知，方案八的作业成本最少，然后依次是方案六、方案七、方案四、方案五、方案二、方案三、方案一，目前棉花的田间作业项目基本已全部机械化，因此棉花种植规模较多的方案作业成本相对较高。

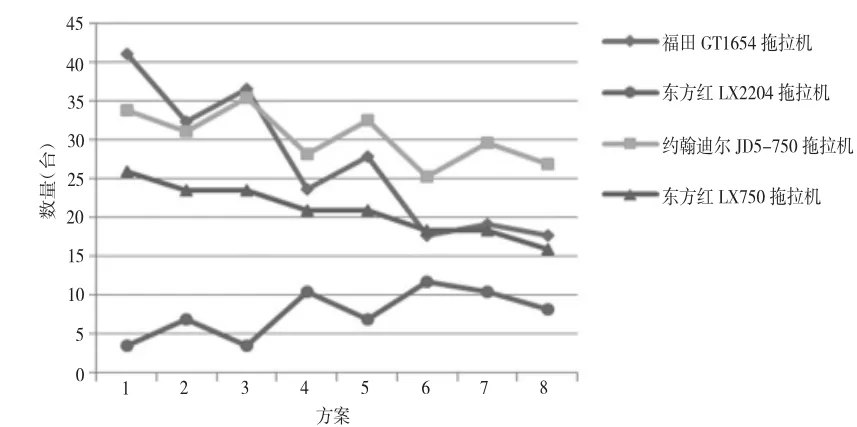
图1　动力机械数量变化趋势

由图1可知，随着棉花种植规模的减少，动力机械中，东方红LX2204拖拉机的数量逐渐增加，而其余3种拖拉机数量都在减少，且福田TG1654拖拉机数量减少幅度较大。

图2　收获机械数量变化趋势

由图2可知，随着棉花种植规模的减少，收获机械中，采棉机数量稳定减少，番茄收获机和小麦联合收割机数量都在增加，且小麦联合收割机的变化波动较大。

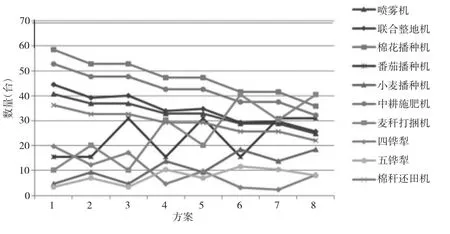
图3　农机具数量变化趋势

由图3可知，随着棉花种植规模的减少，棉花播种机、中耕施肥机、联合整地机、喷雾机、棉秆还田机的数量稳定减少，四铧犁数量先减少后增加，而五铧犁数量先增加后减少。其余农机数量都在增加，其中番茄播种机、麦秆打捆机数量变化波动较大。

3　结论

本文对105团的主要农作物建立了不同种植规模的农机配备模型，采用Lingo软件对全部模型进行求解，并对多种配备方案进行比较分析。从作业成本来看，由于棉花现已实现全程机械化，在一定程度上减少了人力的使用，但机械作业成本较高，这类种植规模可在今后考虑实践，且相同农作物的种植地块最好相对集中，减少成本。本文可对105团在今后种植规模以及配备方案的选取上提供相关建议，使效益最大化。

参考文献：

[1]张静.新疆玉米主栽区农机系统优化配置与规模经营的研究[D].新疆农业大学，2014.

[2]Audsley E.An arable farm model to evaluate the commercial viabilityofnewmachinesortechniques[J].JournalofAgricultural EngineeringResearch,1981(26):135～149.

[3]Whitson R E,Kay R D,Lepori W A,et al.Machinery and crop selection with weather risk[J].Transactions of the ASAE,1981,24(2):288～291+295.

[4]D.A.Bender,D.E.Kline,B.A.McCarl.Postoptimallinerprogramming analysis of farm machinery[J].Transactions of ASAE,1990,33(1):15～20.

[5]张宏文，欧亚明，吴杰.运用线性规划对农机具进行最佳配备[J].农机化研究，2002（1）：59～61.

[6]程敬春.花园乡小麦机械化生产系统优化配置研究[D].新疆农业大学，2012.

[7]张威，曹卫彬，李卫敏等.新疆兵团农场农机具配备的数学建模与优化研究[J].农机化研究，2014（6）：70～72+93.

[8]李鑫尧.安哥拉马兰热农业开发区农机优化配置研究[D].新疆农业大学，2014.

[9]董升涛，段兰昌，胡军等.对俄新友谊农场农业机械配备的研究[J].农业机械，2014（19）：158～163.

[10]王新农，孙学光.新疆生产建设兵团统计年鉴，中国统计出版社，2017.

[11]陈华友，周礼刚，刘金培.数学模型与数学建模[M].北京:科学出版社，2014：146～150.