改进蚁群算法的三维激光点云聚类方法

江　珊，吕京国，李现虎

(北京建筑大学测绘与城市空间信息学院，北京 102616)

近年来，点云分割方面取得了很多成果。Herman Gross[1]采用从点云中提取线特征的方法，通过计算最大特征值和特征向量，利用提取的特征线实现点云的分割，结果表明线曲率特征适用于流形结构的点云。Bisheng Yang[2]采用移动LiDAR点云利用路面反射率探测路面信息，首先采用内插生成具有几何参照的点云图像，然后通过反射率强度值分离非地面点，试验表明该算法适用于路面特征的提取。Rostislav Hulik[3]提出了基于三维霍夫变换的连续平面的点云分割算法，通过对比PCL点云库的随机一致性采样算法，证明了算法的稳健性。

随着人工智能的发展，研究者开始关注群智能算法的点云分割研究。林望[4]提出了基于多维粒子群算法(MD-PSO)的散乱点云非监督分类方法，依据PSO聚类和RANSAC建立了稳健的非监督平面分割目标函数，为了防止陷入局部最优，每一维度改进策略的粒子全局最优加入到MD-PSO算法中，试验表明对平面分割具有较高的精度。许多研究者利用蚁群算法来解决分割，分类和类似的问题[6-10]。Ni Shihong提出了基于改进蚁群算法的连续空间优化方法[11]。蚁群算法在其他领域[12-17]也有许多其他方面的应用。

本文的内容为：首先，采用改进信息素残留系数的模型，通过网格划分连续区间变量优化投影方向，实现蚁群优化的投影寻踪点云聚类；然后，评估树木和建筑数量及位置的准确性；最后，基于DUNN指数对蚁群聚类结果的有效性进行评价。

1　改进的蚁群优化投影寻踪聚类算法

从投影时是否需要计算投影密度函数角度，投影指标分为非密度型投影指标和密度型投影指标。前者最常用的是方差指标，后者最常用的是Friedman-Tukey指标。本文所选择的投影指标为后者。假定多指标样本集合为

{y(i,j)|i=1,2，…,n；j=1,2，…,m}

式中，n为样本的个数；m为指标的个数；y(i,j)为第i个样本的第j个指标值。

首先，进行多指标样本集合的预处理，完成样本指标集合的归一化工作，达到消除各指标值的量纲和统一各指标值的变化范围的目的。针对样本集合的归一化问题，存在两种可选策略。第一种情况是越大越优的指标，采用如下归一化策略：y(i,j)=(y(i,j)-ymin(j))/(ymax(j)-ymin(j))；第二种情况是越小越优的指标，采用如下归一化策略：y(i,j)=(ymax(j)-y(i,j))/(ymax(j)-ymin(j))；以上两式中，ymin(j)、ymax(j)分别为多元指标样本集合中第j个指标值的最小值和最大值。

其次，构造投影指标函数。假设a(j)为投影方向向量(单位长度向量)，样本i以a(j)为投影方向的一维投影值为

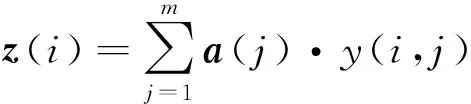
(1)

那么优化投影方向的依据就是构造投影指标函数Q(a),最佳投影方向就是指标达到极大值时的投影方向。分类策略根据一维投影序列{z(i)|i=1,2,…,n}的一维散布图，则优化投影要求z(i)的散布应满足：从局部角度上，投影点应该尽可能呈密集状态，表现为凝聚成若干点团；从整体角度上，各个投影点团之间尽可能呈散布状态。因此投影指标函数可以构造为

Q(a)=SzDz

(2)

式中，Sz为一维投影值z(i)的标准差，表示类别之间的散开度；Dz为一维投影值z(i)的局部密度，代表类内密集度。公式如下

(3)

式中，E(z)为一维投影序列{z(i)|i=1,2,…,n}的均值；R为数据特征的局部密度的窗口半径，R的取值应该满足两个条件，一是包含在窗口内投影点个数不能太少，二是抑制Dz随n增大的幅度，那么R的取值影响投影方向，计算时一般取值为0.1Sz或rmax+m/2≤R≤2m，其中rmax=max[r(i,j)]；rij=|z(i)-z(j)|为点间距值，如果rij≤R，则归为同一类，否则为不同的类；I(R-rij)为单位阶跃函数，如

(4)

然后，估计最佳投影方向，因为所构造的投影指标函数Q(a)随投影方向a变化而变化，所以求解投影指标函数的最大值就可以得到最优投影方向。求解模型为

(5)

以上数学模型是一个以{a(j)|j=1,2,…,m}为优化变化的非线性优化问题，采用蚁群算法来求解连续空间的最优化问题，与遗传算法相比效率与性能较高。

最后，进行聚类分析；将求解后的最优投影方向a*(j)代入一维投影值z(i)的公式为

(6)

计算出各样本点的投影值z*(i)，并比较z*(i)和z*(i+1)的接近程度，如果二者越接近，那么样本i和i+1就归为同一类。

投影寻踪算法中投影方向的优化是一种连续空间的优化问题，其目标函数为非线性问题，那么采用蚁群算法相比传统的解析法、网格法与遗传算法，它具有较高的效率和精度，并且对目标函数与约束函数并无连续性和偏导数存在性的要求。依据现有的关于蚁群连续空间优化的研究文献，蚁群算法在连续空间优化的方法一般分为两种：第一种是信息量函数分布的蚁群优化算法；第二种是简单连续优化问题的蚁群算法。本文提出改进信息素残留系数的蚁群算法，优化投影寻踪投影方向，实现三维点云的最佳聚类。

本文蚁群优化投影寻踪算法过程为：

(1) 针对投影方向中各变量的取值范围，ajk≤aj≤aij(j=1,2,…,m)，m为样本的指标数目，采取在变量区间内划分网格的方法，将变量的取值状态映射到空间网格点上，那么蚂蚁在各个空间网格点上的移动将依据各网格点上的目标函数值，并且释放出不同的信息量，就可以影响下一群蚂蚁的移动方向；经过一定时间的循环之后，目标函数值小(或大)的网格点上信息量残留就比较大，以信息量的大小作为判断准则，选择信息量大的空间网格点，以此来缩小变量的变化区间，那么蚁群就在此点附近移动；重复以上过程，直到网格间距小于一定的阈值后(或满足其他条件)，则投影方向的优化过程终止。

(2) 将投影方向aj分为n等份，那么投影方向中m个变量取值的选择问题就变为m级决策问题，每一级存在n+1个节点，则总计有(n+1)m个节点。将第1级到第m级所选择的各节点连接起来，构成解空间中的一个解，见表1。

表1投影状态空间的解

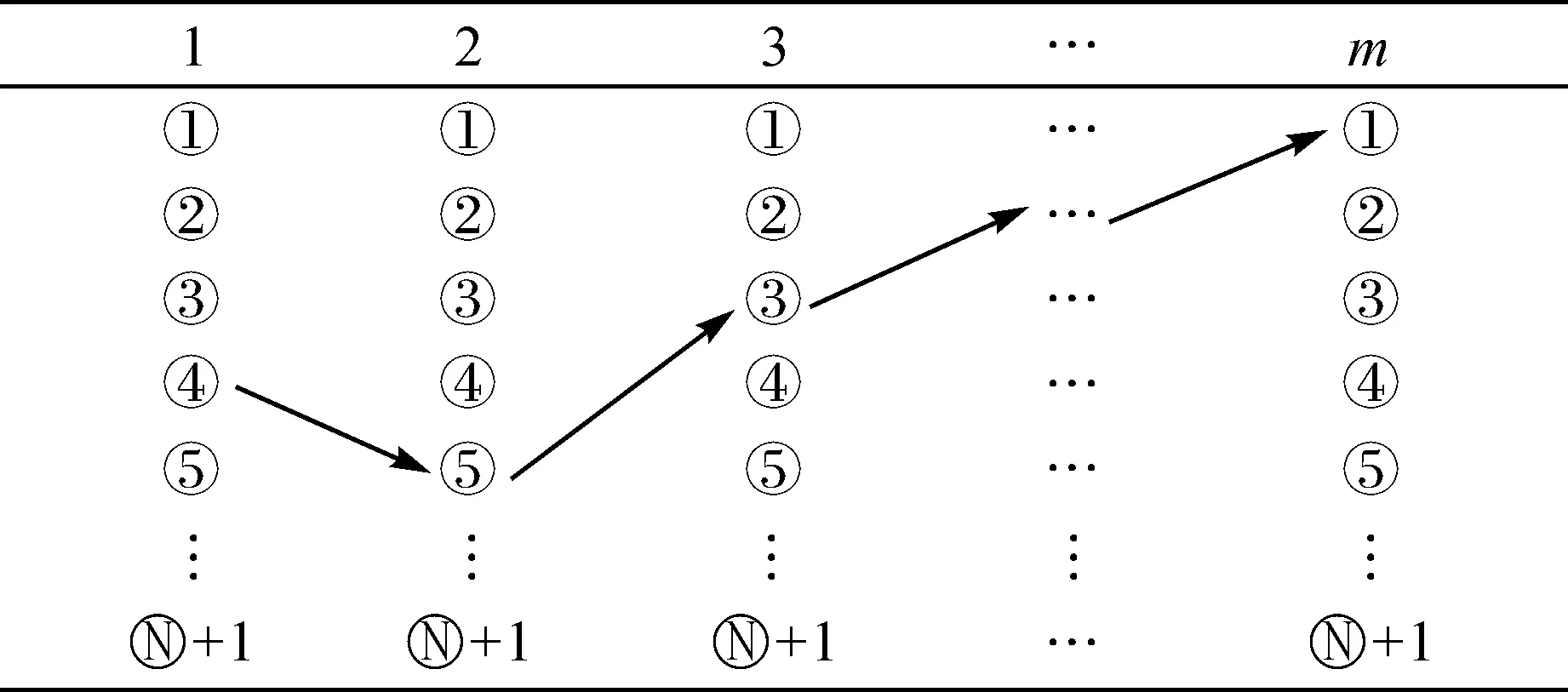
从表1可知，投影方向的状态为(4,5,3,…,1)，那么其所对应的解为

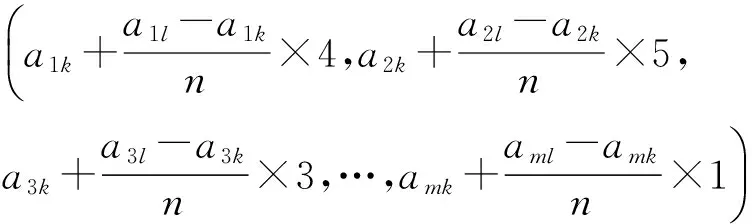
(7)

结合改进的蚁群算法求解投影向量，首先，需要改进蚁群连续空间寻优的状态转移规则。假设每一级设定1只蚂蚁(或更多)，蚂蚁总数为m(或更多)，将每一只蚂蚁的评价函数定义为相邻点之间的目标函数差值,Δfij=fi-fj,∀i,j。那么对限定在本级节点之间移动的每一只蚂蚁的转移概率pij为

(8)

式中，τij为每一只蚂蚁在邻域内的信息素强度，表达了第j节点对第i节点的吸引强度；Ak表示蚂蚁k在下一步可以经过的空间网格点集合。最初，蚂蚁散布在网格点中，记录评价函数值最佳的位置，依据以上转移概率公式移动每一只蚂蚁，按照最邻近原则进行搜索，如下所示：

其次，需要改进蚂蚁在连续空间寻优的信息素更新策略。信息素更新公式为

(9)

式中，ρ为信息素的残留系数，表达了信息强度的持久性，其值影响收敛的全局性与速度，一般取值为0.5～0.9之间。因为ρ越大，收敛就越快，但搜索就越易于陷入局部最优解，而ρ越小，全局搜索的能力就会提高，但搜索速度就会降低，因此对ρ提出了基于对数反正切函数的自适应更新策略，即ρ随迭代次数的反正切函数而发生改变，这样既保证了全局收敛性能，也提高了算法的收敛速度。Q为一正数，fk为目标函数值。ρ的更新公式为

(10)

式中，nc为迭代次数；参数a为控制迭代次数变化的加速度。

2　点云聚类试验分析

2.1　改进蚁群优化投影寻踪聚类试验

在试验中，用坐标x，坐标y，坐标z，法矢量(x,y,z方向)，曲率共7个特征来分类点云。为了使投影指数函数Q(a)达到最大值，必须同时优化7个参数。从本质上讲，它是一个多维的优化问题。本文采用改进的蚁群优化投影寻踪聚类算法。蚁群算法的参数见表3，改进后算法中的蚂蚁数目为变量的数量m=7，轨迹的相对重要性alpha=0.9，能见度的相对重要性beta=2.0，按照信息素进行转移的概率为q0=1，迭代次数的初始值为nc=1，各路径的信息素tau=0，各路径能见度为1。最大迭代次数是500。各个变量分为100等分,并将蚂蚁随机分布在每个变量的某一个区间内，其中ε为0.001。点云分割及提取的植物和建筑物结果如图1、图2所示。

图1　点云分割的植物和建筑物结果

图2　提取植物和建筑物的结果

图2左图为树，右图为建筑物。

本文试验用的点云数据为徕卡ALS60 sn/6133在太子港获取的机载激光雷达数据，其飞行高度约为760 m。本文使用交互式操作，从点云中提取树木和建筑物。通过设置不同的参数来提取树木和建筑物。并对树木与建筑物的数量与准确性进行评估。见表2和表4。

表2　树木与建筑物位置和数量的精度

表3　蚁群算法的参数

如表2所示，通过计算建筑物和树木的数量和位置可以看出，本文提出的方法适用于精确测定树木和建筑物的位置。

本文提出的改进的蚁群优化投影寻踪聚类与传统的蚁群优化投影寻踪聚类效果比较一致。与其他两种算法相比，本文提出的算法在迭代次数上较少，时间复杂度相对较低，这源于信息素残留系数的更新方式影响了迭代次数，对于连续空间寻优速度起着很重要的作用。最佳投影方向各个分量的大小反映了各个特征对点云分类的影响程度，从最佳投影方向可知，对点云的分类影响程度大小依次为坐标x、坐标y、法矢量、曲率和坐标z。

3　结　论

本文深入分析了蚁群算法在点云聚类中应用的计算原理，并将该模型与其他聚类模型相结合应用于三维点云的聚类中。总结如下：

(1) 深入分析蚁群算法在连续空间优化的原理，通过优化信息素残留系数的更新方式，对比了遗传算法优化投影寻踪的效率，实现投影寻踪聚类的最佳投影方向加速选择，为蚁群优化投影寻踪三维激光点云高维度特征的聚类提供指导。研究表明，信息素残留系数是影响连续空间搜索的关键因素，特别是对于大数据量的高维特征投影问题，特征的重要性对分类起到了决定作用，也意味着未来点云聚类研究应该加强特征选择的研究。

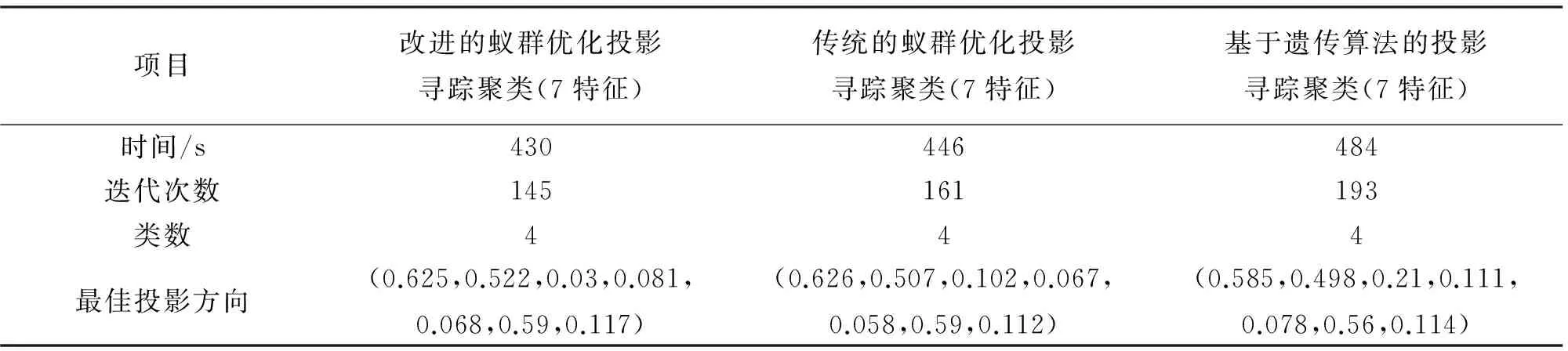
表4　对蚁群算法与其他算法的性能比较

(2) 改进的蚁群优化投影寻踪聚类方法适用于树和建筑物分割。经过试验评估发现，树木的高度和建筑物的结构对结果均有重要影响。一般来说，树或建筑物越高，百分比和定位精度就越好。本文认为这种方法用在其他领域具有可行性。

参考文献：

[1] GROSS H，THOENNESSEN U.Extraction of Lines from Laser Point Clouds[C]∥Symposium of ISPRS Commission Ⅲ：Photogrammetric Computer Vision PCV06.[S.l.]：International Archives of Photogrammetry，Remote Sensing and Spatial Information Sciences，2006：86-91.

[2] YANG B，FANG L，LI Q，et al.Automated Extraction of Road Markings from Mobile LiDAR Point Clouds[J].Photogrammetric Engineering & Remote Sensing，2012，78(4)：331-338.

[3] HULIK R，SPANEL M，SMRZ P，et al.Continuous Plane Detection in Point-cloud Data Based on 3D Hough Transform[J].Journal of Visual Communication and Image Representation，2014，25(1)：86-97.

[4] WANG L，CAO J，HAN C.Multidimensional Particle Swarm Optimization-based Unsupervised Planar Segmen-tation Algorithm of Unorganized Point Clouds[J].Pattern Recognition，2012，45(11)：4034-4043.

[5] BIOSCA J M，LERMA J L.Unsupervised Robust Planar Segmentation of Terrestrial Laser Scanner Point Clouds Based on Fuzzy Clustering Methods[J].ISPRS Journal of Photogrammetry and Remote Sensing，2008，63(1)：84-98.

[6] GUPTA S，WEINACKER H，KOCH B.Comparative Analysis of Clustering-based Approaches for 3-D Single Tree Detection Using Airborne Fullwave LiDAR Data[J].Remote Sensing，2010，2(4)：968-989.

[7] REITBERGER J，SCHNÖRR C，KRZYSTEK P，et al.3D Segmentation of Single Trees Exploiting Full Waveform LiDAR Data[J].ISPRS Journal of Photogrammetry and Remote Sensing，2009，64(6)：561-574.

[8] LEE H，SLATTON K C，ROTH B E，et al.Adaptive Clustering of Airborne LiDAR Data to Segment Individual Tree Crowns in Managed Pine Forests[J].International Journal of Remote Sensing，2010，31(1)：117-139.

[9] OTERO F E B，FREITAS A A，JOHNSON C G.A New Sequential Covering Strategy for Inducing Classification Rules with Ant Colony Algorithms[J].IEEE Transactions on Evolutionary Computation，2013，17(1)：64-76.

[10]XIAO J，ADLER B，ZHANG J，et al.Planar Segment Based Three-dimensional Point Cloud Registration in Outdoor Environments[J].Journal of Field Robotics，2013，30(4)：552-582.

[11]NI S，QIN J，SU C.Dynamic AntColony Algorithm Used in Continuous Space Optimization[J].Electronics Optics and Control，2009，16(12):12-14.

[12]KHANNA K，RAJPAL N.Reconstruction of Curves from Point Clouds Using Fuzzy Logic and Ant Colony Optimization[J].Neurocomputing，2015，161(8)：72-80.

[13]PARPINELLI R S，LOPES H S，FREITAS A A.An Ant Colony Algorithm for Classification Rule Discovery[J].Data Mining：A Heuristic Approach，2002：191-208.

[14]HEMMATEENEJAD B，SHAMSIPUR M，ZARE-SHAHABADI V，et al.Building Optimal Regression Tree by Ant Colony System-Genetic Algorithm：Application to Modeling of Melting Points[J].Analytica Chimica Acta，2011，704(1)：57-62.

[15]AFSHAR M H.Partially Constrained Ant Colony Optimization Algorithm for the Solution of Constrained Optimization Problems：Application to Storm Water Network Design[J].Advances in Water Resources，2007，30(4)：954-965.

[16]杨德贺，袁静，王秀英，等.形变观测数据的多异常形态统一识别[J].地球物理学报，2017,60(12)：4623-4632.

[17]杨德贺，王秀英，申旭辉，等.钻孔应变观测数据的分形特征研究[J].科学技术与工程，2017,17(34)：73-79.