一种基于SARIMA的经验对流层延迟模型
2018-04-08刘中流甘祥前梁春丽
刘中流,任 超,甘祥前,梁春丽
(1. 桂林理工大学测绘地理信息学院,广西 桂林 541004; 2. 广西空间信息与测绘重点实验室,广西 桂林 541004)
GNSS精密定位技术已广泛应用于测量改正的各个领域。然而GNSS信号穿过大气层时会引起大气延迟误差,这往往对定位精度会产生很大的影响。大气延迟误差主要分为电离层延迟误差和对流层延迟误差。由于电离层对GNSS信号表现出色散介质特性,故产生的电离层延迟与GNSS信号频率相关,因而目前在GNSS常规测量中常采用双频观测方法来消除电离层延迟的影响,且在一定范围内,其对电离层延迟的改正可达90%以上[1]。然而对流层对GNSS信号表现出了非色散介质特性,因此双频观测方法不适用于对流层延迟改正。对对流层延迟改正的常用方法有外部修正法、参数估计法和模型改正法[2-3],它们可以通过采集或运算的方法估计出ZTD值,再代入GNSS观测方程中便可进行延迟误差改正[4]。
改进对流层模型一直是减弱对流层延迟影响的有效方法[5-6],而近年来,部分学者在预测估计ZTD的领域进行了研究,并获得了一定的成效:王勇等使用BP神经网络的方法,在试验中取得了76%的预测值与真实值偏差(bias)在3 cm以内的成果[7];李剑锋等在试验中使用组合模型的方法,使得试验中的平均预测值精度(均方根误差,下同)达到了14.88 mm[8];吕慧珠等使用谱分析和AR补偿结合的方法,使得试验中的平均预测值精度达到了19.36 mm[9]。此类方法也可以较好地计算出对流层延迟,并代入观测方程中进行误差改正。许多学者将自回归移动平均模型(ARIMA)应用到电离层电子含量的预测中,并取得了较好的成果[10-12],而在对流层预测中对其的应用却很少有。ARIMA模型对非平稳序列具有较好的预测效果,且适用范围广,但却容易在捕捉序列线性与非线性复合性特征时出现精度下降[13]。针对上述情况,本文将ARIMA模型应用于ZTD预测,并引入一种基于季节性自回归移动平均模型(SARIMA)的对流层延迟估计新方法,该方法可分别针对不同的原始ZTD序列进行参数构建,然后进行预测以得到最终结果;针对我国不同地区的ZTD值进行预测,并统计分析它们的预测精度。
1 模型介绍
1.1 自回归移动平均模型(ARIMA)理论
ARIMA是一个可以衡量内生变量与其滞后性与改变量关系的系统模型,是对移动平均模型(ARMA)的扩展[14]。
ARIMA(p,d,q)的实质是ARMA(p,q)的d阶单整(d次差分),其效果是将一个非平稳的时间序列转化为平稳时间序列[15]。设Xt为等时间间隔的ZTD序列,则可将ARMA(p,q)模型表达为
φp(B)Xt=θq(B)εt
(1)
式中,B为滞后算子;εt为白噪声序列;φp(B)为p阶自回归系数多项式,定义其相应特征方程为φp(x);θq(B)为q阶滑动平均系数多项式,定义其相应特征方程为θq(x)。
当原ZTD序列{Xt}不平稳时,可考虑通过式(10)进行差分
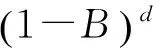
(2)
式中,u为差分算子;d为差分阶数。{Xt}在经过d次差分后变为平稳序列,即可建立ARIMA(p,d,q)模型的一般形式
(3)

1.2 季节性自回归移动平均模型(SARIMA)理论
SARIMA模型又是对ARIMA模型的拓展。虽然ARIMA(p,d,q)模型已经可以解决许多时间序列的拟合预测问题,但在实际操作中,又另有许多时间序列的变化具有明显的周期性特征,我们称之为季节性时间序列。由于时间序列的周期性变化,它们在不同周期内的同时期数据将处于一个相当的水平,此时可以恰当引入乘积季节性SARIMA(p,d,q)×(P,D,Q)模型[16]。当序列间的长期趋势、季节效应和随机波动间不是简单的相加关系时,可以使用ARIMA模型提取短期相关性,用周期步长为S的SARIMA模型提取季节周期性,再采用二者的乘积组合模型对ZTD序列进行预测,从而得到乘积季节模型的完整结构为
(4)


图1 SARIMA模型进行ZTD预测的基本流程
2 试验分析
2.1 数据准备
本文分别选取IGS中心发布的长春站(chan)和上海佘山站(shao)的2016年年积日1—30 d和92—121 d的ZTD数据作为本次分析的原始ZTD数据,数据时间分辨率变为1 h。采用ARIMA和SARIMA模型分别对它们进行预测分析,并评定其精度。预测分析原则为,选取这两个时段前29 d逐小时观测的ZTD数据作为训练数据,并对未来24个ZTD值逐小时地进行预测。
2.2 精度指标
实现对各个ZTD分量序列的SARIMA模型构建后,选取前29 d的数据进行拟合分析,并对后24 h的数据进行预测。本文引入精度指标:均方根误差(root mean square error,RMSE)、平均绝对误差(mean absolute error,MAE)、平均相对误差(mean relative error,MRE),它们的数学表达式分别为
(5)
(6)
(7)
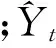
2.3 建模分析
在进行拟合预测前,应对SARIMA模型(或ARIMA模型)进行定阶。此处以上海佘山站1—29 d 原始ZTD数据为例进行模型构建分析,此时段数据如图2所示。

图2 上海佘山站年积日1—29 d ZTD数据
通过观察易于发现,该序列波幅在趋势上下波动且无明显增大或减小倾向,应属于趋势平稳(trend stationary),此时再引入ADF单位根检验法,判断序列是否严平稳。ADF检验结果见表1。
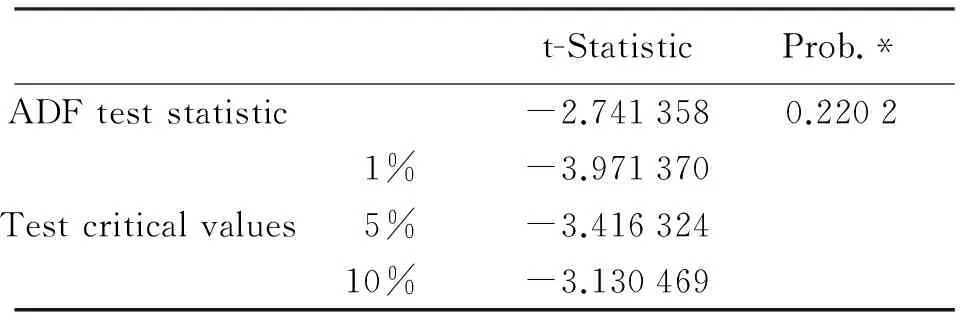
表1 ZTD序列ADF检验结果
结果显示,原序列即使在10%的置信水平上也不能拒绝单位根假设。此时需要对原序列进行一阶差分,并再次进行ADF检验,结果见表2。
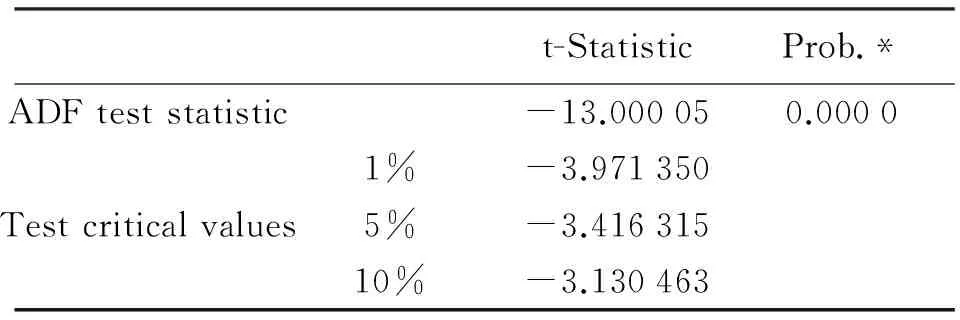
表2 一阶差分ZTD序列ADF检验结果
此时结果显示,即使在1%的置信水平下,也可以拒绝单位根假设,代表序列平稳,故d值取1。下一步应进行相关性分析,作出该一阶差分序列滞后36阶的ACF、PACF函数如图3所示。
由图3可知,其ACF、PACF函数均表现出拖尾性,满足AR(p)、MA(q)过程。此处PACF值三步截尾,一阶滞后处PACF值较为显著,且24阶滞后处再次上升至一个相对峰值,随后更高阶滞后的自相关系数明显减小,此类型表明AR(3)×SAR(24)基本符合该序列(此处SAR(24)仅为计算机的取向概念,告知计算机季节组中的每24 h为一个周期,而该模型应正确描述为p=3,P=1),同理可得q=8,P=1。故可基本选定SARIMA(3,1,1)×(8,0,1)模型。但此时定阶的模型仅代表它能很大程度上迫近原序列,并不代表就是最优模型,此时可选取该模型已确认参数的一定邻域内的正整数替换原参数,并一起进行AIC准则运算,选择使得AIC最小的参数组合确认为最优模型参数。本文通过AIC验证最终确认模型为SARIMA(3,1,1)×(8,0,1),并以此进行回归,再进行残差白噪声检验,残差ACF、PACF函数图如图4所示。
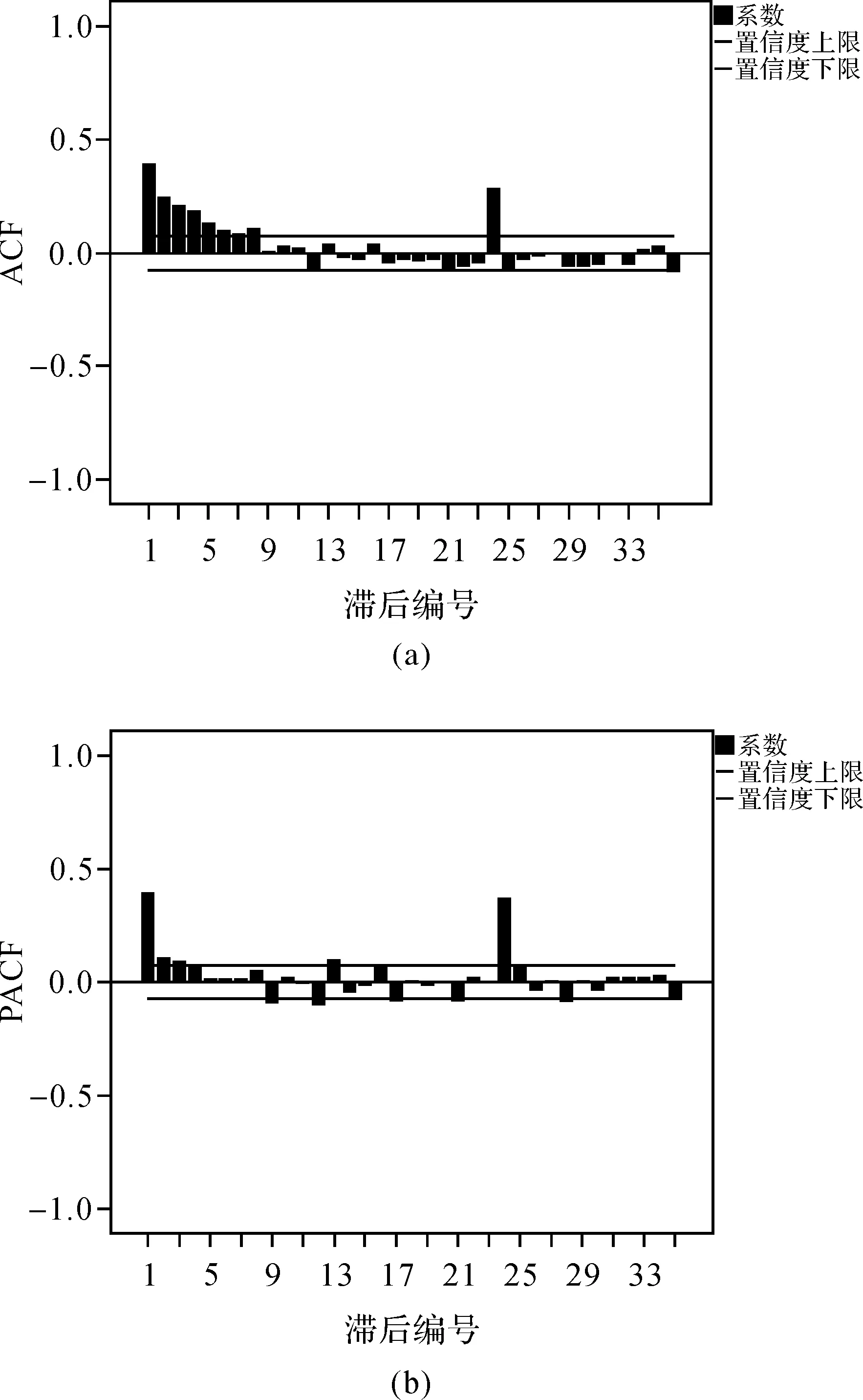
图3 一阶差分ZTD序列ACF、PACF图
显而易见,残差为白噪声序列,故可认为该模型可靠,可进一步用于ZTD数据预测。同理,其他序列也以此过程进行模型定阶,并作预测分析。
2.4 预测分析
对所准备的原始序列进行预测分析,最终得到两模型预测精度对比分别见表3、表4、表5。
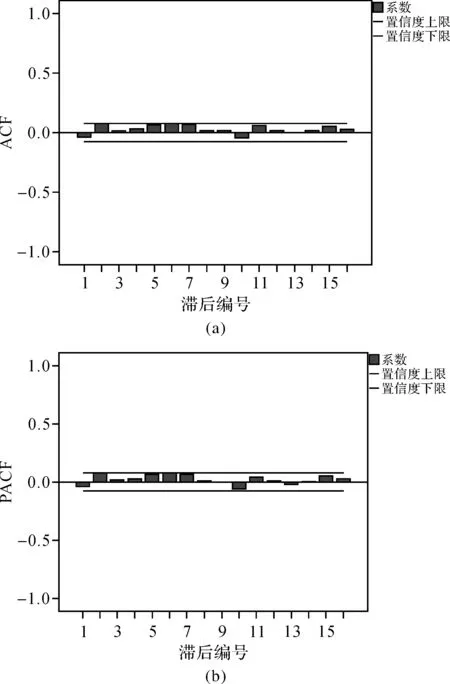
图4 残差序列ACF、PACF图
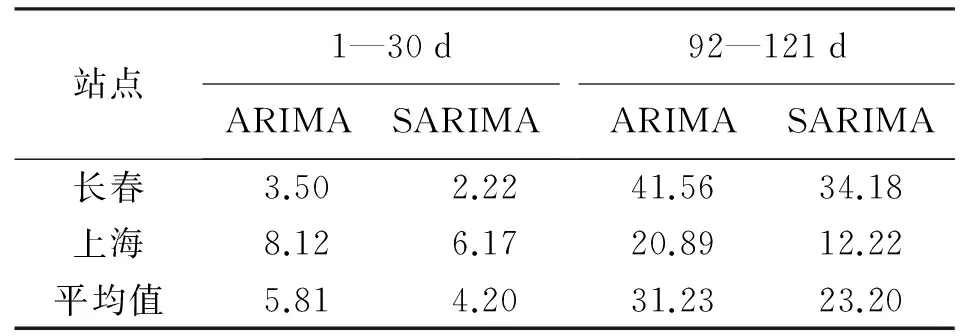
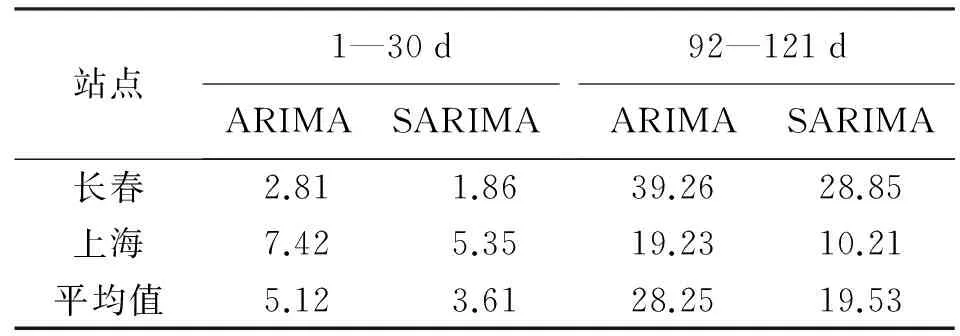
表4 两模型预测成果MAE对比 mm
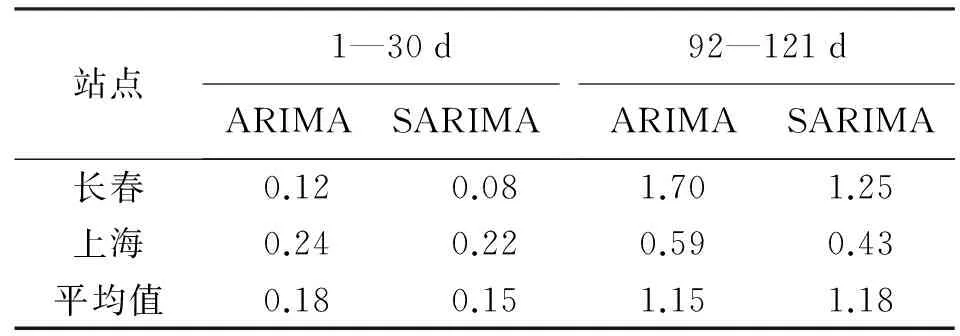
表5 两模型预测成果MRE (%)
本文对上述各表的预测结果进行分析,并总结得到以下结论:
(1) 加入季节性分析后,对ZTD序列的预测精度有较好的提高,对年积日1—30 d的数据预测结果显示,平均RMSE降低了27.7%,对年积日92—121 d的数据预测结果总体精度较前者虽有所下降,但同期平均RMSE也降低了25.7%。
(2) SARIMA模型预测结果显示,平均偏差不大,且占原值比很小,年积日92—121 d的数据预测结果的平均MRE仅1%左右,年积日1—30 d的数据预测结果平均MRE仅0.15%。
(3) SARIMA模型对ZTD数据的总体估计精度较领域内当前的其他模型(前文提及)的估计精度要高,总体平均RMSE降低了19.9%。
(4) 在部分时期、地区出现了预测精度降低的情况,由于对流层延迟受湿度影响较大,故本文猜测与同期气象变化存在关系,但不于此处进行研究。
3 结 论
本文综合分析了中国长春、上海地区的ZTD变化,并分别以ARIMA和SARIMA模型,对两个地区不同时期的ZTD序列进行了短期(24 h)预测。综合不同地区、时段的预测成果,结论如下:
(1) ARIMA和SARIMA模型对ZTD序列均有较好的预测效果,而由于ZTD序列存在一定的季节性特征,故总体而言加入季节性分析后预测精度均有较大提高。
(2) 本文在定阶试验时发现,存在个别ZTD序列不具有较强的季节性特征的情况,此时不能盲目加入季节性影响,否则将降低模型精度。
(3) SARIMA模型对ZTD序列的预测精度较高,可满足许多ZTD数值估计的需求,具有一定的实用意义。
(4) 关于SARIMA模型在不同地区、时期对ZTD序列的预测的应用效果需要进一步研究。
参考文献:
[1] 李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2005.
[2] 赵章明,冯径,洪亮.卫星定位中对流层延迟模型对比分析[J].测绘通报,2016(11):18-21.
[3] 李昭,邱卫宁,邱蕾,等.几种对流层延迟改正模型的分析与比较[J].测绘通报,2009(7):16-18.
[4] 丁晓光.对流层延迟改正在GPS数据处理中的应用与研究[D].西安:长安大学,2009.
[5] 姚宜斌,胡羽丰,余琛.一种改进的全球对流层天顶延迟模型[J].测绘学报,2015,44(3):242-249.
[6] 姚宜斌,张豹,严凤,等.两种精化的对流层延迟改正模型[J].地球物理学报,2015,58(5):1492-1501.
[7] 王勇,张立辉,杨晶.基于BP神经网络的对流层延迟预测研究[J].大地测量与地球动力学,2011,31(3):134-137.
[8] 李剑锋,王永前,郭俊元.预测模型在对流层延迟计算中的应用研究[J].测绘科学技术学报,2015,32(5):450-454.
[9] 吕慧珠,黄文德,闻德保.一种基于频谱分析和AR补偿的对流层延迟预报模型[J].大地测量与地球动力学,2015,35(2):283-286.
[10]刘军,柴洪洲,刘先冬,等.基于ARIMA(p,1,1)的电离层预报模型[J].大地测量与地球动力学,2010,30(3):79-82.
[11]刘立龙,陈军,黄良珂,等.基于小波-ARIMA电离层短期总电子含量预报[J].桂林理工大学学报,2016,36(2):294-299.
[12]张小红,任晓东,吴风波,等.自回归移动平均模型的电离层总电子含量短期预报[J].测绘学报,2014,43(2):118-124.
[13]朱帮助,林健.基于ARIMA和LSSVM的非线性集成预测模型[J].数学的实践与认识,2009,39(12):34-40.
[14]ZHANG G P.Time Series Forecasting Using a Hybrid ARIMA and Neural Network Model[J].Neurocomputing,2003,50(1):159-175.
[15]李子奈.计量经济学[M].北京:高等教育出版社,2000.
[16]张婷.CPI的 SARIMA 模型与X-12季节调整模型对比预测分析[J].经济问题,2014(12):37-41.
