基于GA-ANN融合算法的棉田杂草特征降维及分类识别
2018-04-08王淑芬杨玲香石河子大学理学院新疆石河子832003
王淑芬,杨玲香(石河子大学 理学院,新疆 石河子 832003)
新疆棉花产量占全国棉花产量的1/6,田间杂草是影响棉花产量和品质的一个重要因素。对棉田中不同植物进行有效识别、准确分类,是实现智能化精准除草至关重要的一步。叶片形态特征的准确识别是区分杂草和农作物的关键环节[1],为提高不同杂草识别的准确率,需要对植物多种特征(形状特征、纹理特征、空间颜色特征等)融合应用,但随着特征维数的增加,识别时间及空间复杂度明显提高。如何构建合理有效的算法,实现在众多相互关联的特征中快速、准确地提取有效特征是杂草识别的难点。近年来,遗传算法(Genetic algorithm,GA)、人工神经网络(Artificial neural network,ANN)、支撑向量机(Support vector machine,SVM)等人工智能算法被广泛应用于杂草识别研究。李先锋等[2]提出了基于SVM和D-S证据理论的多特征融合的杂草识别方法,解决了特征空间复杂度和分类维数过高的问题,试验结果表明,多特征决策识别方法的识别率达97%以上。李慧等[3]利用主成分分析(Principal component analysis,PCA)降维得到3个主成分,不但能有效减少SVM的训练时间,而且提高了分类准确率,效果良好。张新明等[4]提出了基于改进概率神经网络的玉米与杂草识别算法,可以实现最优特征选择,提高分类准确率。利用特征融合进行降维研究虽然可以降低分类识别的复杂度,但难以分析特征参数对不同类别杂草影响的显著性。本研究采用GA算法融合ANN的改进算法对棉花及杂草的多种特征参数进行降维提取,并利用自组织特征映射网络(Self-organizing map,SOM)对选取的优良特征参数组合进行网络训练,分析各优良特征之间的相互关系及对分类效果的影响,为通过提取棉花和杂草的显著特征,提高杂草的识别率提供参考。
1 材料和方法
1.1 试验材料
所用图片(图1)均为自然环境下,采用数码相机拍摄的棉花、苘麻、田旋花、龙葵草、灰菜的图像。图像采集时间为2016年4月15日—5月16日。采集地点为石河子大学农学院试验站(45°19′N、86°03′E)。数码相机的型号为SAMSUNG IT100/VLUU IT100/SAMSUNG SL820,分辨率为640×480像素,拍摄距离为离地面50 cm。

a.棉花;b.苘麻;c.田旋花;d.龙葵草;e.灰菜图1 棉花及杂草图像
1.2 图像处理与特征提取
1.2.1图像预处理为了克服光照和阴影的影响,应用归一化的2g-r-b算法[5-6]将彩色图像转化为灰度图像,其中r、g、b由下式确定:
R(x,y)、G(x,y)、B(x,y)分别表示GRB图像的红、绿、蓝三原色所对应的值。然后使用Otsu[7]方法将图像转化为二值图像,将植物从背景中分割出来。二值化后的图像可能存在孔洞和噪声,最后利用形态学算子进行后处理并分离出植物叶片,得到单叶二值图像。
1.2.2形状特征提取不同植物叶片的外观存在一定的差异。在处理后的叶片上提取宽长比S1、伸长度S2、致密度S3共3个无量纲的几何特征,具体公式如下:
其中,W表示叶片最小外接矩形的宽度,L表示叶片最小外接矩形的长度,A表示叶片区域面积,P表示叶片区域边界的周长。
1962年,Hu首先提出代数不变矩的概念,并给出了7个代数矩不变量,被称为Hu不变矩[8]。这个不变矩具有旋转、缩放和平移(Rotation,scale,translation,RST)不变性,常作为有效的形状特征被广泛应用于图像识别领域。对于数字图像f(x,y),其7个Hu不变矩定义为:
其中,ηij由下列公式计算:
r=(p+q)/2+1
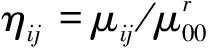
在计算时,为了便于区分,分别对以上7个不变矩取对数,即:
Hi=logφii=1,…,7
这样,便可得到叶片的10个形状特征:[S1,S2,S3,H1,H2,H3,H4,H5,H6,H7]。
1.2.3纹理特征提取选用叶片图像上4个方向(0°、45°、90°、135°)的灰度共生矩阵[9]所对应的特征值来提取纹理特征。设图像f(x,y)的大小为M×N,灰度级为L,行列方向上的距离为dx、dy。灰度共生矩阵是一个二维相关矩阵,用来描述图像在特定方向θ上,相隔为d=(dx,dy)且像素为i、j同时出现的联合概率P(i,j|d,θ),则4个方向的灰度共生矩阵定义如下[9-10]:
P(i,j|d,0°={(x,y)|f(x,y)=i,f(x+dx,y+dy=j),|dx|=d,dy=0}
P(i,j|d,45°={(x,y)|f(x,y)=i,f(x+dx,y+dy=j),|dx|=d,dy=-dx}
P(i,j|d,90°={(x,y)|f(x,y)=i,f(x+dx,y+dy=j),dx=0,|dy|=d}
P(i,j|d,135°={(x,y)|f(x,y)=i,f(x+dx,y+dy
=j),|dx|=d,dy=dx}
对上述灰度共生矩阵进行归一化:
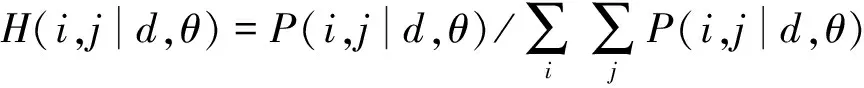
然后提取不同方向的特征值,并求平均作为最后的纹理特征[3]。所对应的纹理特征对比度M1、能量M2、相关性M3、同质性M4和熵M5的具体计算公式如下:
其中,μx、μy和σx、σy分别是相应的边缘分布的均值和标准差。
1.2.4颜色特征提取颜色信息也是区分植物的一类重要特征。文献[11-12]给出了数字图像的颜色矩的定义,即将图像的各个像素点的颜色值当作是一个概率分布,则可用其各阶矩来描述图像。本研究提取HSV空间的H和S分量的前3阶矩共6个特征向量作为颜色特征参数[13],具体表达式如下:
其中,i代表H或S分量,Pij为相应分量的颜色值,N为像素个数。
综上所述,本研究共提取了叶片的21个相关特征作为分类的依据。
1.3 算法理论
1.3.1GA算法GA算法是一种随机搜索的智能方法,是模拟达尔文的遗传学和自然界优胜劣汰的生物进化过程的计算模型[14]。其思想的基本过程如下。
(1)种群初始化:进化代数计数器t=0,最大进化代数T,随机生成M个个体作为初始群体P(0)。
(2)计算个体适应度:对不同问题设置针对性的评价函数,计算群体P(t)中各个个体的适应度。
(3)选择算子设计:对群体进行选择操作。选择的目的是保证群体中的优秀个体能遗传到下一代或通过交叉操作产生新的个体再遗传到下一代。
(4)交叉算子设计:对群体进行交叉操作。交叉算子在遗传算法中起核心作用。
(5)变异算子设计:对群体进行变异操作。变异算子可保持群体的多样性,避免算法陷入局部搜索。
种群P(t)经过选择、交叉、变异运算之后得到下一代种群P(t+1)。
(6)终止条件判断:若t=T,则以进化过程中所得到的具有最大适应度的个体作为最优解输出,终止计算。
1.3.2ANN算法ANN[15-17]是一种模仿动物神经网络的工作特征,进行分布式并行信息处理的数学模型。这种数学模型网络是根据系统的复杂程度,通过不断调整内部大量节点之间的相互连接关系,达到处理信息的目的。它具有自学习、自适应、并行处理等优良特点,在优化计算、智能控制、模式识别、信号处理等方面具有广泛的应用。
BP(Back propagation)网络作为应用最广泛的神经网络模型之一,通过反向传播不断地调整网络的参数,使网络误差平方和最小。在输入模式样本较少的情况下,2层BP网络就可以了,当输入模式样本很多时,需要增加一个隐层,隐层节点数如果太少,网络容错性差,在识别新的输入样本时效果不理想,隐层节点数如果太多,会导致学习时间过长。通常隐层节点数的设置与求解问题的具体要求、输入输出的单元数目都有密切的关系。
SOM网络是一种无导师的学习网络,接受外界的输入模式时会分成不同的区域,各区域对不同输入模式产生各自的响应特征,实现分类的目的。其学习规则是“胜者为王”,当输入一个样本时,寻找与其最为相似的竞争层神经元,就是获胜神经元。以获胜的神经元为中心,调整周围其他神经元的权值,调整的结果是使竞争层的特定神经元变得对输入层的某些样本敏感,从而达到分类的目的。自组织特征映射图可保留各模式的拓扑关系,便于有效、直观地研究各特征对分类结果影响的显著性。
1.3.3GA-ANN融合算法在杂草分类识别中,如果利用全部特征参数,一方面加大了数据量的计算,另一方面由于某些特征的重复性和交叉显现特点,容易导致分类识别率偏低的问题。当神经网络模型的输入样本(即影响因素)维数过高、各变量因素不相互独立时,容易导致所建立的模型精度低、建模时间长等问题。因此,在建立模型之前,有必要对输入样本的分量进行优化选择,将冗余自变量去掉。本研究考虑GA算法优良的全局搜索性能、并行计算能力及可扩展性,融合神经网络模式识别功能及SOM神经网络多维图形可视化优势,利用GA-ANN融合算法进行数据降维及分类识别。以样本的21个特征参数进行遗传编码,为保证GA算法初始群体的均匀分布,采取rand函数生成初始群体,通过神经网络模式识别函数计算的分类精度可评估特征参数不同组合分类结果的优劣,在求得最优特征组合的基础上,利用SOM神经网络的可视化优势,分析各个特征对分类结果的影响。图2显示了GA-ANN融合算法流程。
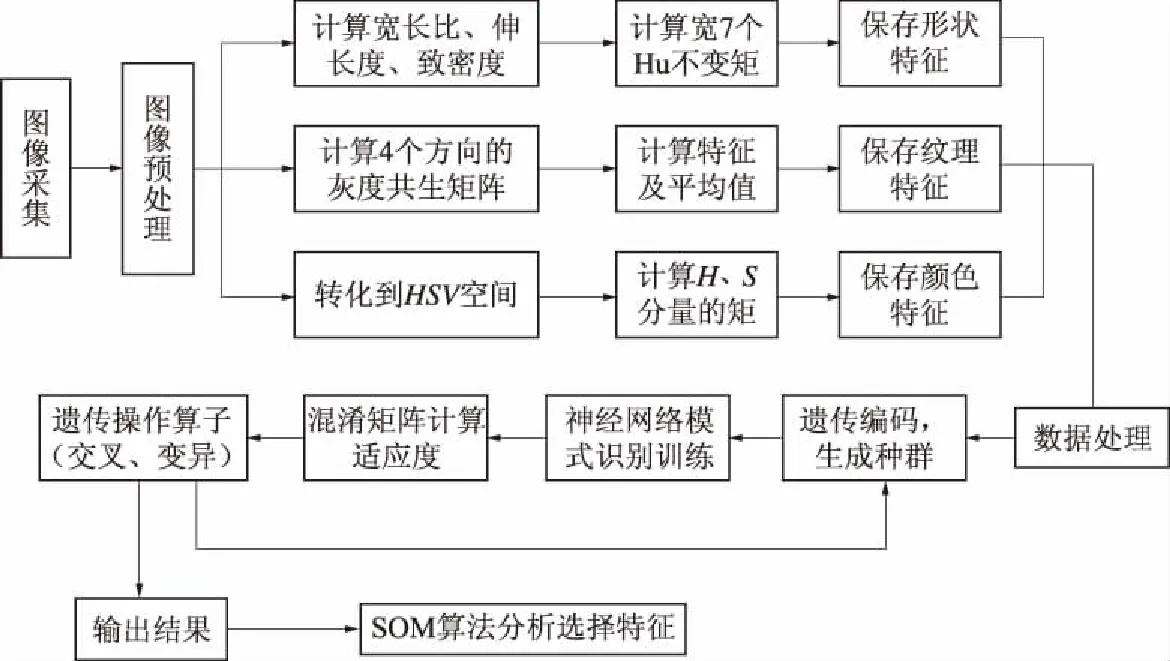
图2 GA-ANN融合算法流程
2 结果与分析
为了验证GA-ANN融合算法对分类识别的有效性,本研究选用棉花和杂草共195个样本的21个特征参数进行数值模拟,并与利用全部特征参数及PCA降维处理的识别准确率进行了对比。结果表明,改进的GA-ANN融合算法不仅能减少数据冗余,简化计算量,而且筛选出的主要特征具有独立性、可区分性、数量少的特点,能有效应用于分类识别,提高分类精度。
2.1 神经网络模式识别函数patternnet分析
模式识别函数patternnet中,通过采用经验公式与逐步试验法,设置隐含层神经元个数为20,trainFcn函数选择trainlm,此训练函数对中等规模的前馈网络(多达数百个连接权)是最快速算法;Performance function默认值是crossentropy。图3为模式识别网络的训练模型,在遗传算法初始群体的生成过程中,会选取不同特征组合,具体选取的特征个数为图3中输入变量的个数。图4为混淆矩阵,行代表了预测类别,列代表了数据的真实归属类别,对角线元素为准确预测的样本数目。
2.2 GA-ANN融合算法结果分析
本研究对GA-ANN融合算法模型进行了仿真试验。在GA-ANN融合算法中,种群个体数设置为30,迭代次数设置为20,采取精英保留策略,每次可得600个不同的特征组合,从中获取全局最优特征组合。进行随机独立仿真试验100次,特征组合的总数可达60 000个,得到100组优良特征组合,其平均分类准确率稳定在98%左右。表1列出了融合算法获得的部分优良特征组合。从表1可以看出,第8组特征组合的分类准确率达到99.87%。与利用全部特征参数及PCA分析降维后的分类准确率进行了对比,利用全部特征虽然分类准确率可以达到一个相对较高的水平,但考虑样本特征参数数量众多,特征参数相互之间交叉的情况,很容易造成数据冗余,计算缓慢;而PCA分析降维法的分类准确率相对较低。试验结果表明,改进的GA-ANN融合算法可有效地将特征参数缩小为8~13维,并保证良好的分类效果。
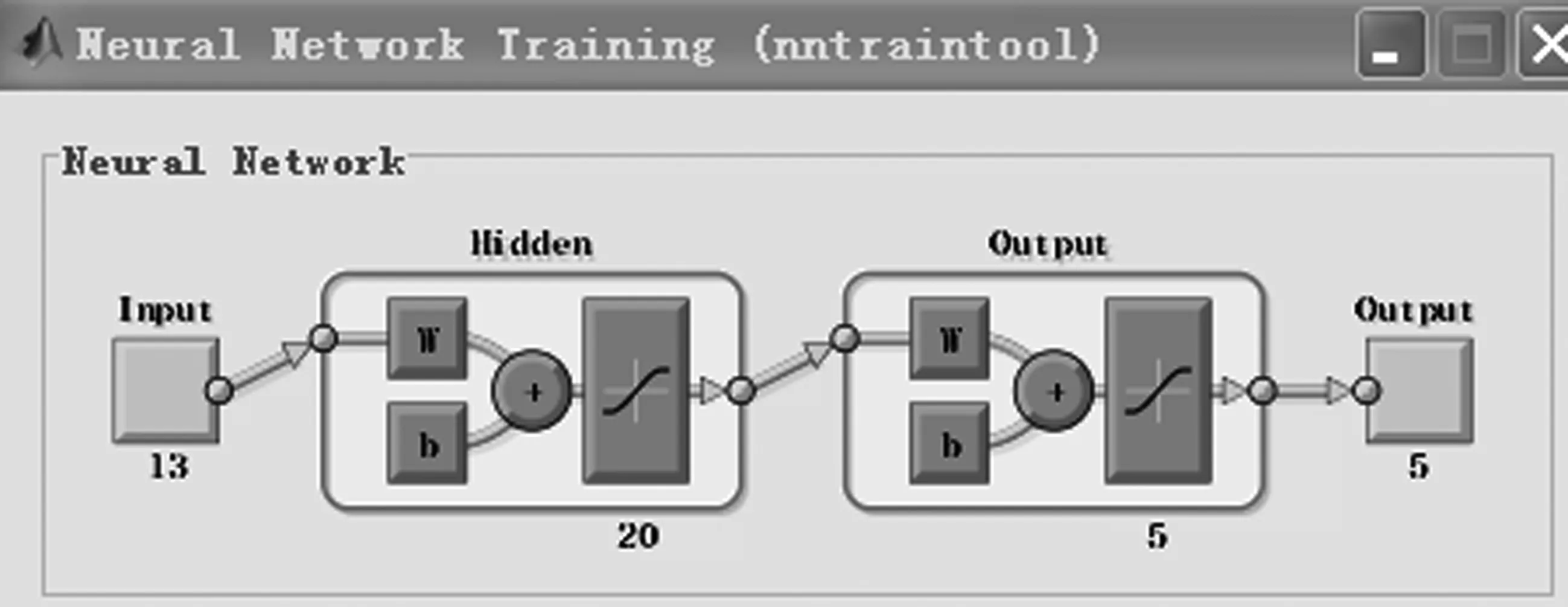
图3 模式识别网络训练模型
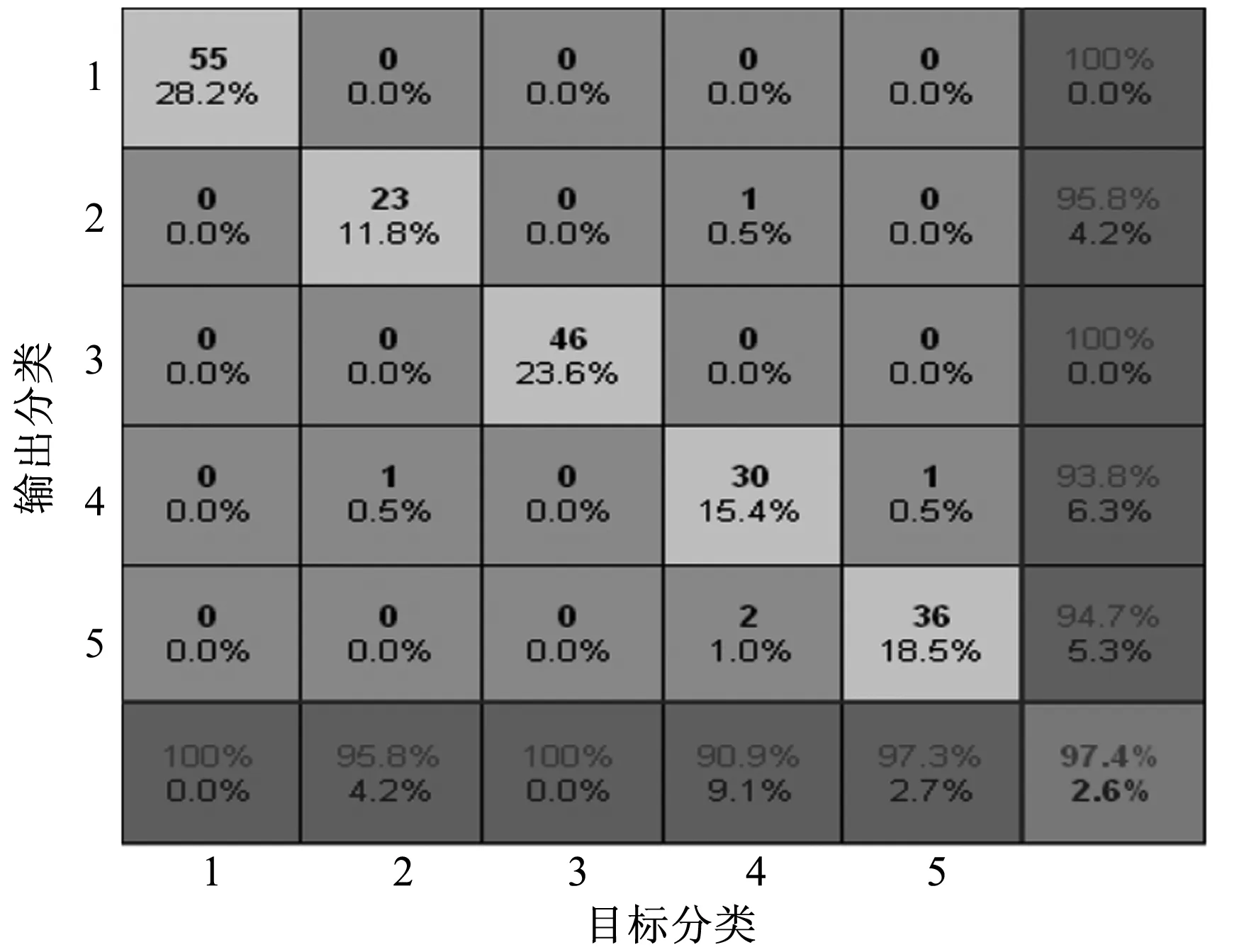
图4 混淆矩阵
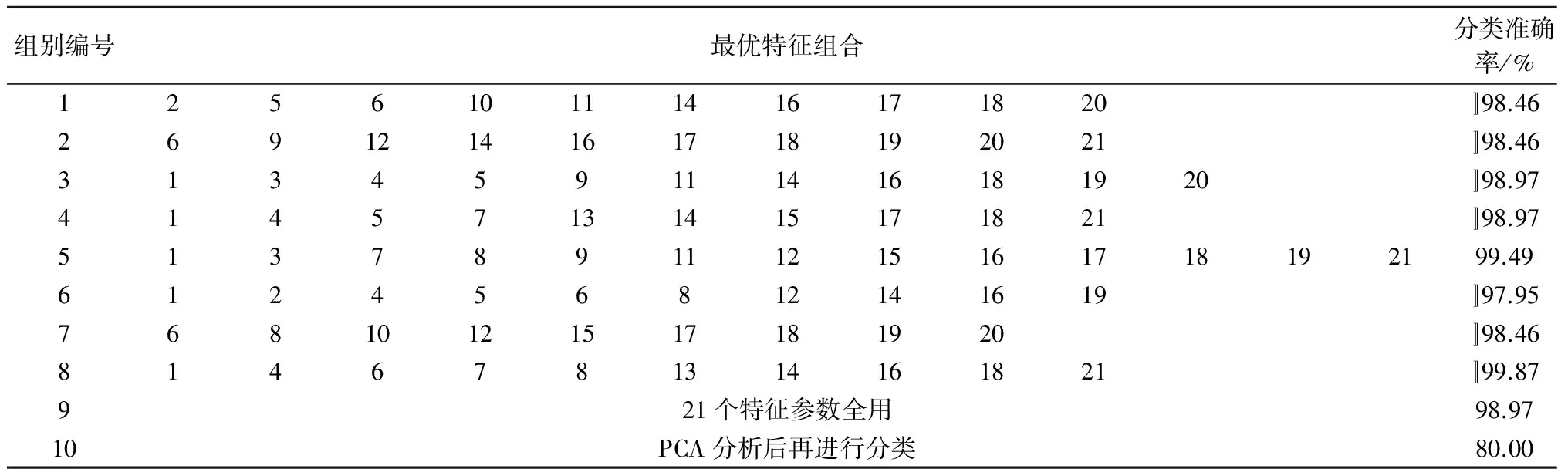
表1 融合算法获得的部分优良特征组合
2.3 降维特征参数组合的SOM神经网络分析
为深入研究选取的各特征参数对分类准确率的影响以及它们之间的相关性,利用SOM神经网络对选取特征参数组合进行网络训练,195个样本分为5类:原始样本1—55为棉花样本,56—79为苘麻样本,80—125为田旋花样本,126—158为龙葵草样本,159—195为灰菜样本。选取表1中特征组合分组相对均匀、准确率最高的第8组进行SOM分析。在第8组中序号1、4、6、7、8、13、14、16、18、21分别对应参数宽长比、Hu不变矩1、Hu不变矩3、Hu不变矩4、Hu不变矩5、能量、同质性、H一阶矩、H三阶矩、S三阶矩。在selforgmap函数中,网络输出层拓扑结构设置为[5,1],邻域大小的初始值为1,拓扑函数为hextop,距离函数为linkdist,最大迭代次数设定为200次。
分类结果如图5所示,第1类55个为棉花样本,第2类24个中包含23个苘麻样本和1个错分样本,第3类43个中包含31个龙葵草样本和12个错分样本,第4类29个中包含25个灰菜样本和4个错分样本,第5类44个中包含43个田旋花样本和1个错分样本。分类准确率为90.70%。
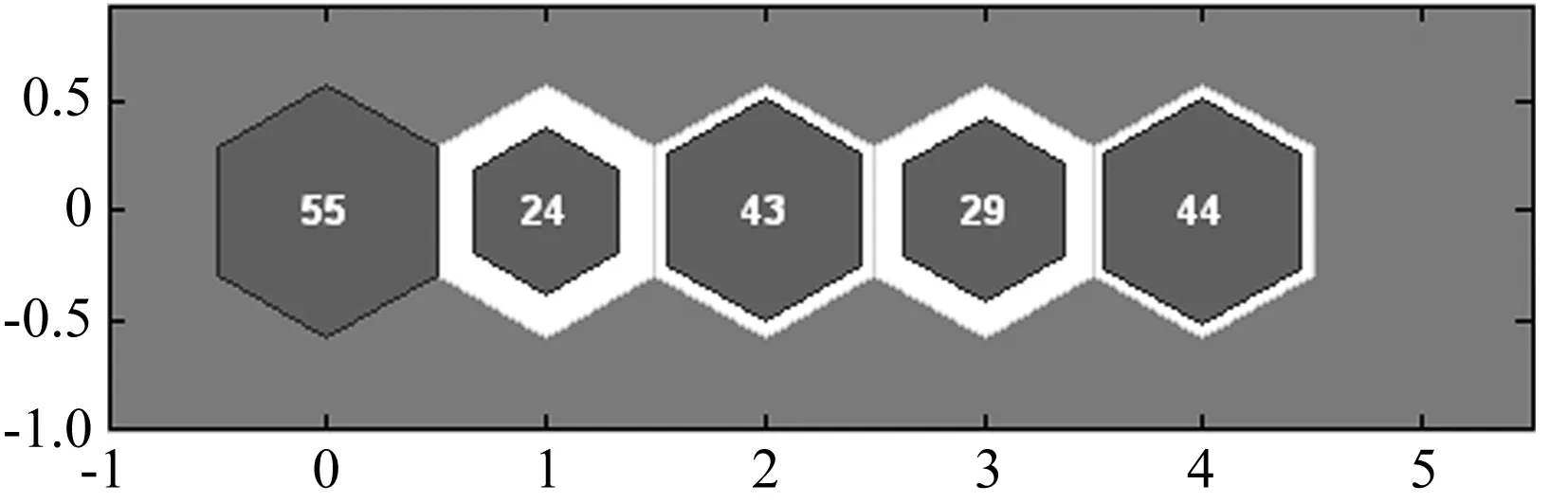
神经元形状为六边形,其位置依次为(0,0)、(1,0)、(2,0)、(3,0)、(4,0),六边形内数字为该类别包含样本数量图5 样本分类结果
图6中从左到右5个神经元(棉花、苘麻、龙葵草、灰菜、田旋花)依次通过不同颜色的六边形相连,六边形颜色从黑色到红色到黄色表示不同神经元之间距离的远近,可以看出,第2类(苘麻)、第3类(龙葵草)和第4类(灰菜)样本神经元相邻,特征差异性较小,在分类中容易出现错分的现象,而第1类(棉花)和第5类(田旋花)样本神经元不相邻,有显著的特征差异性,因而分类效果较好。
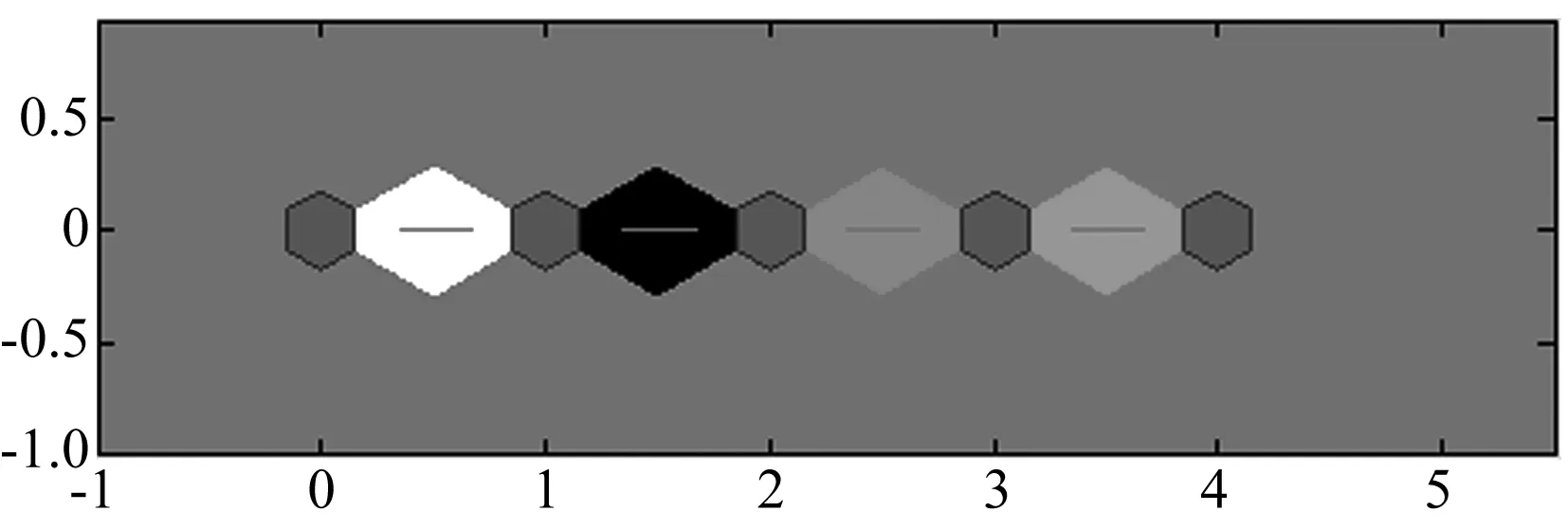
小六边形为神经元,大六边形表示两神经元邻近,大六边形颜色表示神经元距离的远近图6 神经元邻域加权距离映射图
图7中的输入变量1—10分别对应表1中第8组的特征参数1、4、6、7、8、13、14、16、18、21。每一个特征参数权重分布图中,六边形颜色从黄色到红色到黑色依次表示特征参数对不同类别杂草分类影响的强弱。总体从颜色上观察,不同样本差异性显著,表明经过融合算法降维后选取的特征,对各个类别的影响呈现出独立性、可区分性的显著特点。苘麻、龙葵草、灰菜样本的各参数权重,大多2类或3类颜色接近,说明这3类样本特征差异性不明显,在分类中易混淆。而棉花和田旋花的各参数权重图颜色与其余3类差异性明显,因而分类效果较好。棉花样本神经元在1、18序号对应的宽长比、H三阶矩权重图中呈现黄色,表明宽长比、H三阶矩与棉花样本的分类准确率呈强相关性;在4、13、16、21序号对应的Hu不变矩1、能量、H一阶矩、S三阶矩权重图中呈现黑色,表明这4类特征与棉花样本的分类准确率相关性不显著;其余特征参数根据神经元颜色从黑色到红色再到黄色的变化,对棉花样本分类准确率的影响逐步加强。
根据各参数权重分布图颜色的差异,对各特征参数与苘麻、龙葵草、灰菜、田旋花4类样本的分类准确率进行同样的相关性分析。1序号对应的宽长比与苘麻样本分类准确率呈强相关性,16、18、21序号对应的H一阶矩、H三阶矩、S三阶矩与苘麻样本分类准确率具有一定的相关性,其余特征参数对苘麻样本分类准确率的影响不显著。1、16、21序号对应的宽长比、H一阶矩、S三阶矩与龙葵草样本的分类准确率呈较强相关性,6、13、14、18序号对应的Hu不变矩3、能量、同质性、H三阶矩与龙葵草样本的分类准确率具有一定的相关性。6、16、21序号对应的Hu不变矩3、H一阶矩、S三阶矩与灰菜样本的分类准确率呈强相关性,其余特征参数与灰菜样本的分类准确率具有一定的相关性。对比苘麻、龙葵草、灰菜样本的显著性特征参数发现,H一阶矩、S三阶矩对3类样本的影响呈现共性,导致分类效果不理想。4、7、8、13、14序号对应的Hu不变矩1、Hu不变矩4、Hu不变矩5、能量、同质性与田旋花样本的分类准确率呈强相关性,6、16、21序号对应的Hu不变矩3、H一阶矩、S三阶矩与田旋花样本的分类准确率具有一定相关性,1、18序号对应的宽长比、H三阶矩特征与田旋花样本的分类准确率相关性较弱。对比1、18序号特征对棉花和田旋花的影响可以发现,差异性显著,因此这2类样本特征区分明显,分类效果良好。
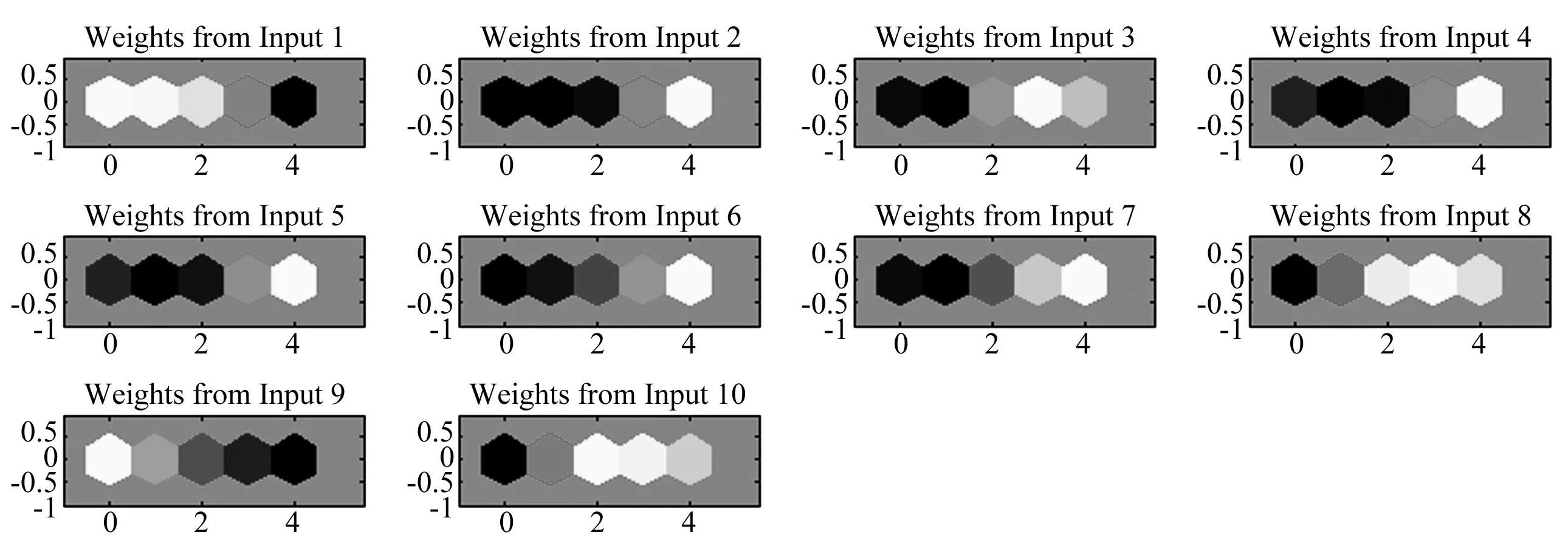
10个小图形中六边形颜色反映不同特征参数对5种植物分类影响的权重大小图7 输入参数权重分布图
3 结论与讨论
提高田间杂草的识别率在高效、精准除草工作中起着至关重要的作用,为农作物的优质高产奠定基础。植物叶片的形状特征、纹理特征、空间颜色特征等参数可用于区分农作物与不同类别杂草,研究人员利用模式识别算法开展了大量杂草分类研究工作[1-4],然而,对于植物叶片提取后的优良特征参数与植物类别的相关性研究较少。本研究提取了棉花与4类杂草叶片的21种特征参数,将特征参数进行遗传编码,利用神经网络模式识别算法构造适应度函数,遗传算法收敛的最优解对应提取的优良特征组合,可有效降低特征参数空间的复杂度。仿真试验结果表明,融合算法降维后获得的100组优良特征组合模型分类准确率稳定在98%左右,特征参数维数缩小为8~13维。融合算法与利用全部特征参数的模型比较,在保证分类准确率的前提下,特征空间复杂度明显降低,与PCA分析法降维的分类准确率相比,提高了约18个百分点。进一步采用SOM对降维后的特征参数进行了网络训练,结果表明:宽长比、H三阶矩特征对棉花样本分类影响显著,H一阶矩、S三阶矩对棉花样本分类影响不显著,而对苘麻、龙葵草、灰菜样本的分类影响显著,同时其也是田旋花样本多个显著特征参数中的2个。此结果与李先锋等[18]在特征优化后保留的最优特征子集相似程度较高,建议棉田杂草数据采集和图像处理阶段,加强与棉花样本分类准确率有强相关性特征参数的提取。
参考文献:
[1]金小俊,陈勇,孙艳霞.农田杂草识别方法研究进展[J].农机化研究,2011,33(7):23-27.
[2]李先锋,朱伟兴,孔令东,等.基于SVM和D-S证据理论的多特征融合的杂草识别方法[J].农业机械学报,2011,42(11):164-168.
[3]李慧,祁力钧,张建华,等.基于PCA-SVM 的棉花出苗期杂草类型识别[J].农业机械学报,2012,43(9):184-189.
[4]张新明,涂强,冯梦清.基于改进概率神经网络的玉米与杂草识别[J].山西大学学报(自然科学版),2015,38(3):432-438.
[5]吕朝辉,陈晓光,吴文福,等.用BP神经网络进行秧苗图像分割[J].农业工程学报,2001,17(3):146-148.
[6]Woebbecke D M,Meyer G E,Von Bargen K,etal.Color indices for weed identification under various soil,residue,and lighting conditions[J].Transactions of the ASABE,1995,38(1):259-269.
[7]Otsu N.A threshold selection method from gray-level histograms[J].IEEE Transactions on Systems,Man,and Cybemetics,1979,9(1):62-66.
[8]李先锋.基于特征优化和多特征融合的杂草识别方法研究[D].镇江:江苏大学,2010.
[9]Haralick R M,Shanmugam K,Dinstein I.Textural features for image classification[J].IEEE Transactions on Systems,Man,and Cybemetics,1973,3(6):610-621.
[10]黄艳丽.基于整体局部颜色特征和纹理特征的图像检索算法研究[D].兰州:兰州大学,2012.
[11]Stricker M A,Orengo M.Similarity of color images[C]//Proceeding of SPIE 2420-Storage and retrieval for image and video databases Ⅲ.San Jose,USA:The International Society for Optical Engineering,1995:381-392.
[12]Stricker M,Dimai A.Spectral covariance and fuzzy regions for image indexing[J].Machine Vision and Applications,1997,10(2):66-73.
[13]张少博,全书海,石英,等.基于颜色矩的图像检索算法研究[J].计算机工程,2014,40(6):252-255.
[14]王小平,曹立明.遗传算法:理论、应用与软件的实现[M].西安:西安交通大学出版社,2002.
[15]楼顺天,施阳.基于Matlab的系统分析与设计:神经网络[M].西安:西安电子科技大学出版社,2000.
[16]蒋宗礼.人工神经网络导论[M].北京:高等教育出版社,2001.
[17]周开利,康耀红.神经网络模型及其MATLAB仿真程序设计[M].北京:清华大学出版社,2006.
[18]李先锋,朱伟兴,纪滨,等.基于特征优化和LS-SVM的棉田杂草识别方法[J].农业机械学报,2010,41(11):168-172.
