循环钻进过程中井筒温度场新模型

王江帅 ，李军 ，柳贡慧 ，2，杨宏伟 ，王超 ，宋学锋

（1.中国石油大学（北京）石油工程学院，北京 102249；2.北京工业大学机械工程与应用电子学院，北京 100192）

0 引言

准确计算井下循环温度，对钻井工程的影响很大，它不仅关系到钻井安全和固井质量，而且对井筒压力平衡、井壁稳定、井下工具强度设计等具有重要的指导作用［1-5］；因此，准确预测井筒温度分布及其变化规律，对安全高效钻进具有重要意义。国内外很多学者对井筒温度进行了深入研究［6-13］，建立的模型基本分为全瞬态模型和半瞬态模型2种，已有研究成果为准确预测井筒温度提供了可靠的依据。然而，利用现有的全瞬态模型求解井筒温度场时，需要计算地层温度，计算过程繁琐，计算量相对较大，而且现有模型也很少考虑在循环钻进过程中钻屑的进入对环空内钻井流体热学性能的影响。

针对以上不足，本文在传热学基本原理的基础上，充分考虑了钻井过程中岩屑进入环空后对流体热学性能的影响，建立了循环钻进过程中井筒温度场的计算新模型，并给出了模型求解步骤及稳定性判断依据。所建模型形式简洁、求解方便，可为井筒温度场的准确计算提供理论指导。

1 物理模型

在正常钻井作业中，钻井液由井口进入钻柱内，然后经过钻头喷嘴进入环空，在井底混合岩屑上返至井口（见图1）。钻井液循环期间，地层与环空钻井液进行热交换，环空钻井液与钻柱内钻井液进行热交换。钻井液在井内的整个循环过程，可以看作是一个具有一定边界条件的热交换器。

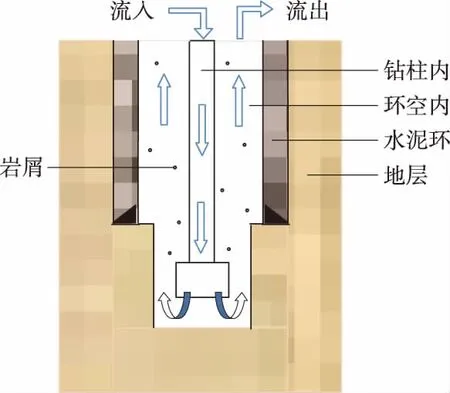
图1 井筒物理模型

2 数学模型

2.1 假设条件

在建立井筒温度数学模型时，进行以下假设：1）钻杆内和环空内流体温度在径向上不发生变化；2）井筒向外一定距离处，地层温度为原始地温（Holmes等［14］认为不受扰动的地层半径为3.05 m，本文选取该值作为原始地温位置与井眼中心轴线的距离）；3）忽略摩擦生热；4）短时间低钻速钻进时，忽略进尺对井深的影响；5）考虑岩屑进入环空对流体传热的影响；6）将地层与水泥环的热性能视为相同。

2.2 温度场模型的控制方程

考虑井筒内流体流动方式（见图2），根据热力学第一定律，即微元体内能量增量等于进入微元体的净热流量与外界对微元体做的功之和，针对钻杆内和环空内流体分别建立控制方程。

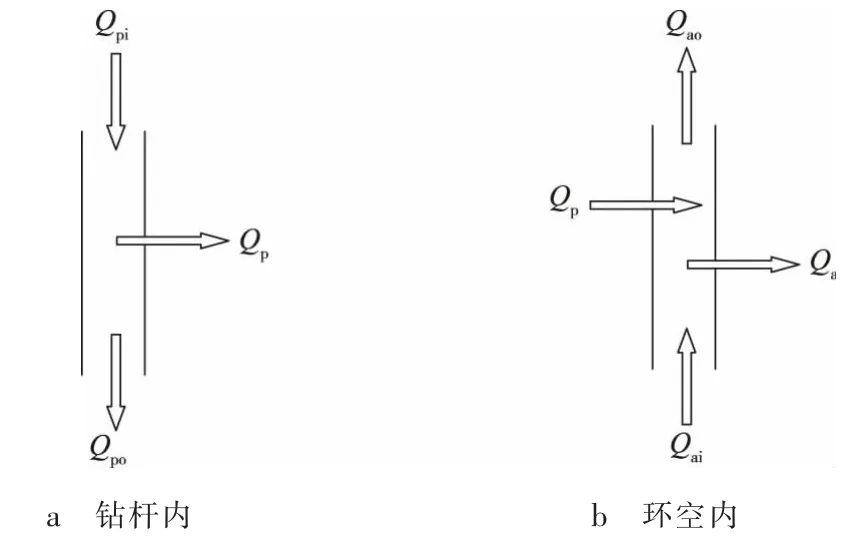
图2 井筒内流体传热示意

2.2.1 钻杆内温度场控制方程

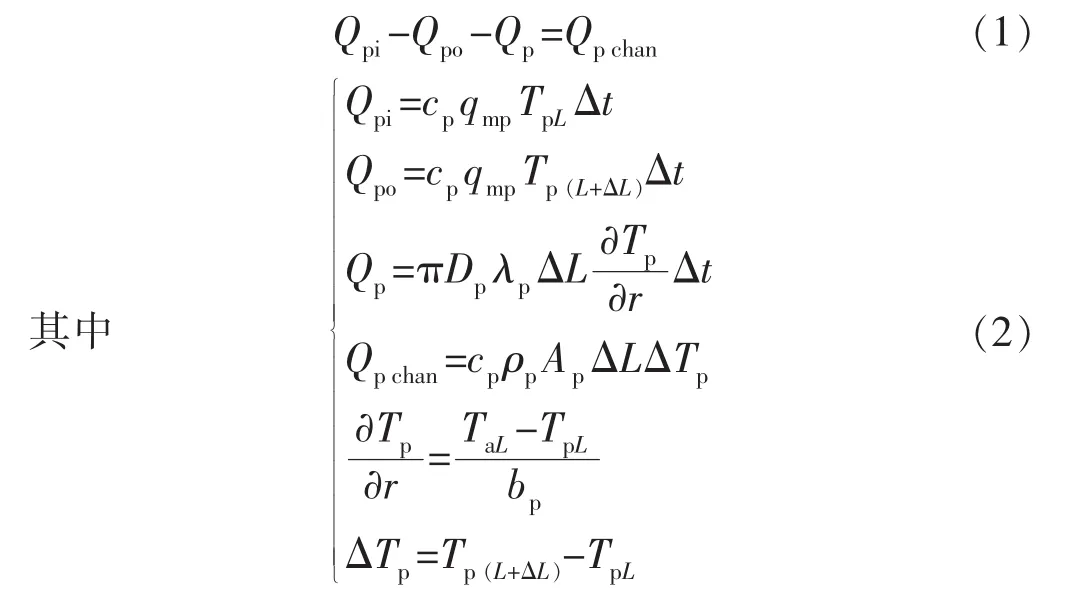
将式（2）代入式（1）中，化简可得：

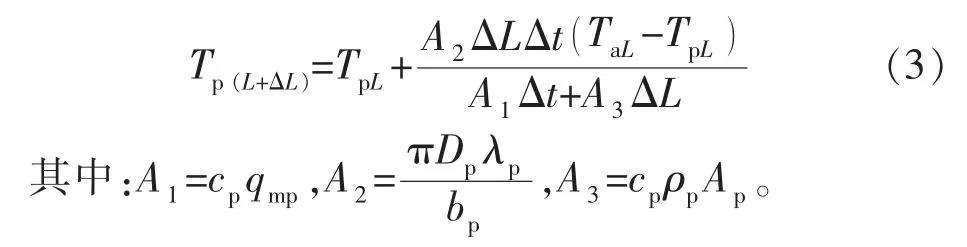
式中：Qpi，Qpo分别为钻杆内流入、流出流体的热量，J；Qp为钻杆与环空之间的传热量，J；Qpchan为钻杆内微元体内流体热量的改变量，J；cp为钻杆内流入流体的比热容，J/（kg·℃）；qmp为钻杆内流入流体的质量流量，kg/s；TpL，Tp（L+ΔL）分别为流入、 流出钻杆内微元体的流体温度，℃；L为任意微元体的位置深度，m；ΔL为微元体的长度，m；Δt为时间步长，s；Dp为钻杆外径，m；λp为钻杆的导热系数，W/（m·℃）；r为径向位移，m；Tp为钻杆内流体温度，℃；ρp为钻杆内流入流体的密度，kg/m3；Ap为钻杆内流体流动的面积，m2；TaL为环空内流体温度，℃；bp为钻杆的壁厚，m。

2.2.2 环空内温度场控制方程

将式（5）代入式（4）中，化简可得：

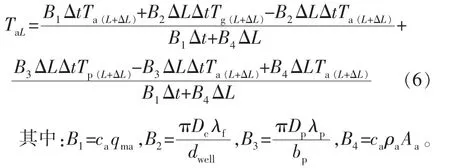
式中：Qai，Qao分别为环空内流入、流出流体的热量，J；Qa为环空与地层之间的传热量，J；Qachan为环空内微元体内流体热量的改变量，J；ca为环空内流入流体的比热容，J/（kg·℃）；qma为环空内流入流体的质量流量，kg/s；TaL，Ta（L+ΔL）分别为流入、 流出环空内微元体的流体温度，℃；Tg（L+ΔL）为深度 L+ΔL 处的原始地层温度，℃；Dc为温度为地温位置处的圆柱外径，m；λf为井壁的导热系数，W/（m·℃）；Twell为井眼和温度为地温位置处之间的温度，℃；dwell为井眼和温度为地温位置处之间的距离，m；ρa为环空内流入流体的密度，kg/m3；Aa为环空内流体流动的面积，m2。

2.3 温度场模型的辅助方程

由于环空内有岩屑进入，因此改变了环空混合流体的热学性能。

混合流体的密度为

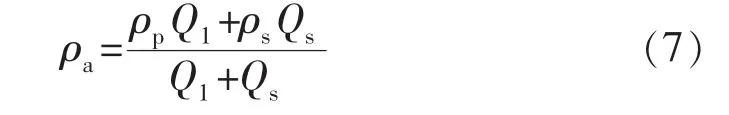
混合流体的质量流量为

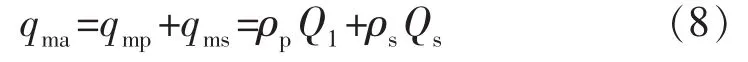
混合流体的比热容为

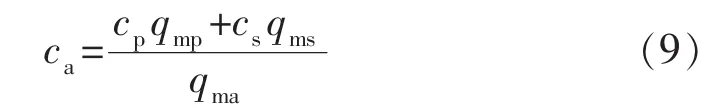
式中：ρs为岩屑的密度，kg/m3；Q1为钻井液排量，m3/s；Qs为岩屑的产生速率，m3/s；cs为岩屑的比热容，J/（kg·℃）；qms为岩屑的质量流量，kg/s。

3 模型求解

采用迭代方法对井筒温度场模型进行求解，具体求解步骤如下：1）假定环空温度为原始地温，即，利用式（3）计算出i时刻钻杆内微元体的流体温度分布；2）将钻杆内温度代入式（6），计算 i时刻环空内微元体的流体温度分布；3）将计算得到的环空温度再次代入式（3），重新计算钻杆内温度分布；4）将钻杆温度代入式（6）中，重新计算环空内温度分布。重复步骤3）和4），当环空温度分布满足式（10）时，认为计算结果稳定。

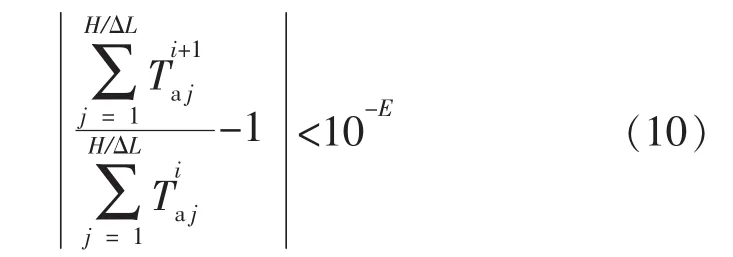
模型计算结果的稳定性取决于E值，模拟分析了E值对模型计算结果稳定性的影响规律（见图3）。

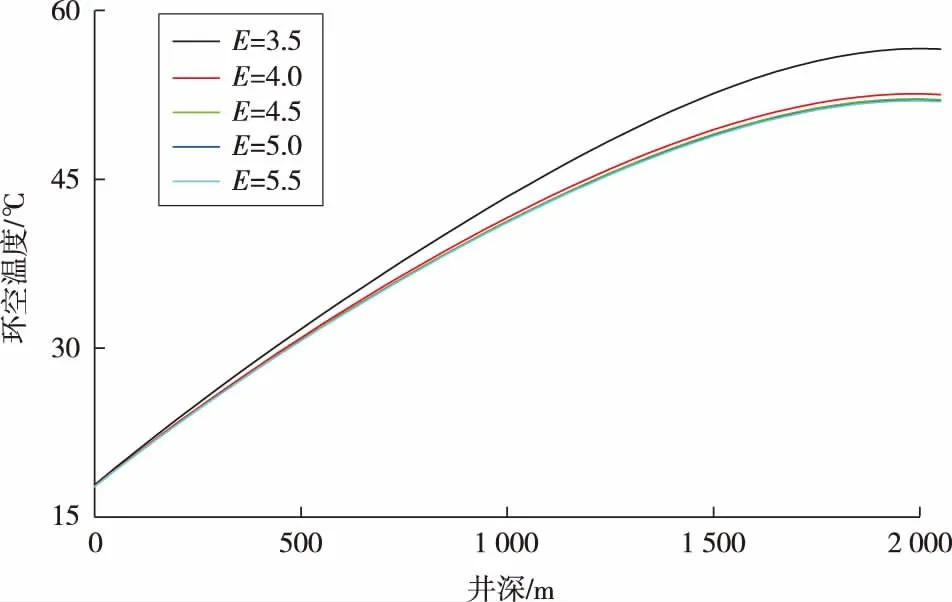
图3 E值对模型计算结果稳定性的影响

由图3可以看出，当E值大于4.0时，计算结果趋于稳定，无任何不稳定问题。建议根据不同的井眼几何尺寸、钻井流体及地层特性，寻求最优的E值。

4 实例分析

4.1 实例1

利用冀东油田某井实测温度数据对模型的合理性进行对比验证。现场施工的工艺流程为起钻—安装测量短节—下钻—循环钻进，钻井基础数据及热物性参数见表1。

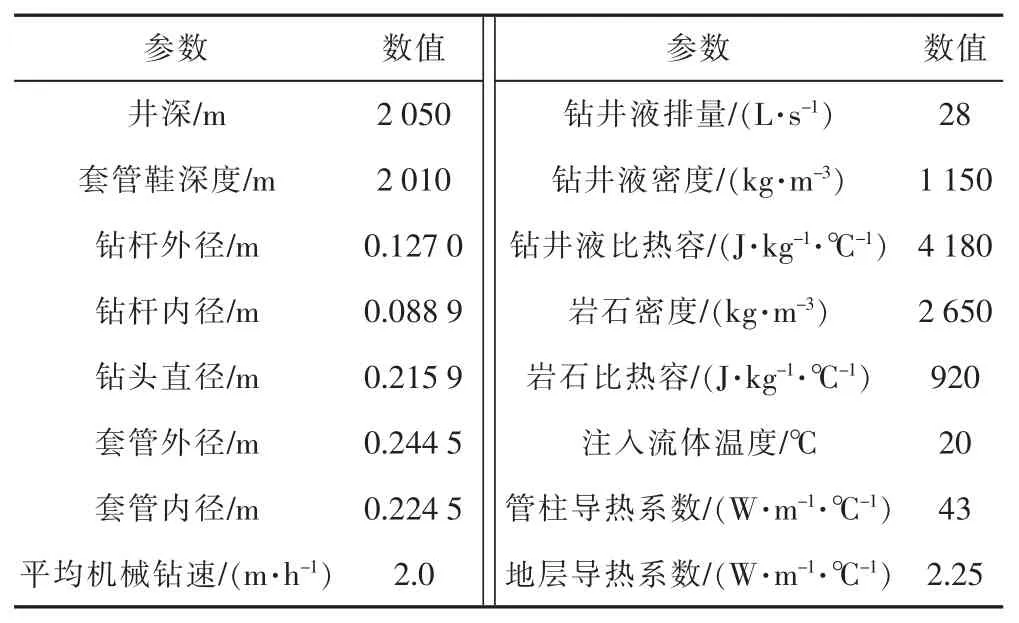
表1 钻井基础数据及热物性参数

循环钻进期间，用本文模型模拟计算的环空井底温度值与实测值基本吻合（见图4）。计算得到的井底最高温度稳定在51℃，与实测值的最大误差不超过2℃。整个循环期间模拟计算值与实测值的最大误差不超过7.3%，精度满足工程需要，表明本文井筒温度场模型计算结果符合现场实际情况。

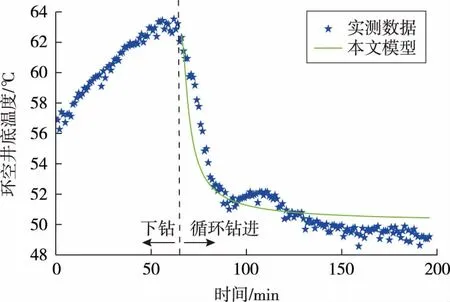
图4 循环钻进期间模型计算结果与实测数据对比

4.2 实例2

利用文献［15］中N23井的实测数据进行对比验证。钻井基础数据及热物性参数见表2。

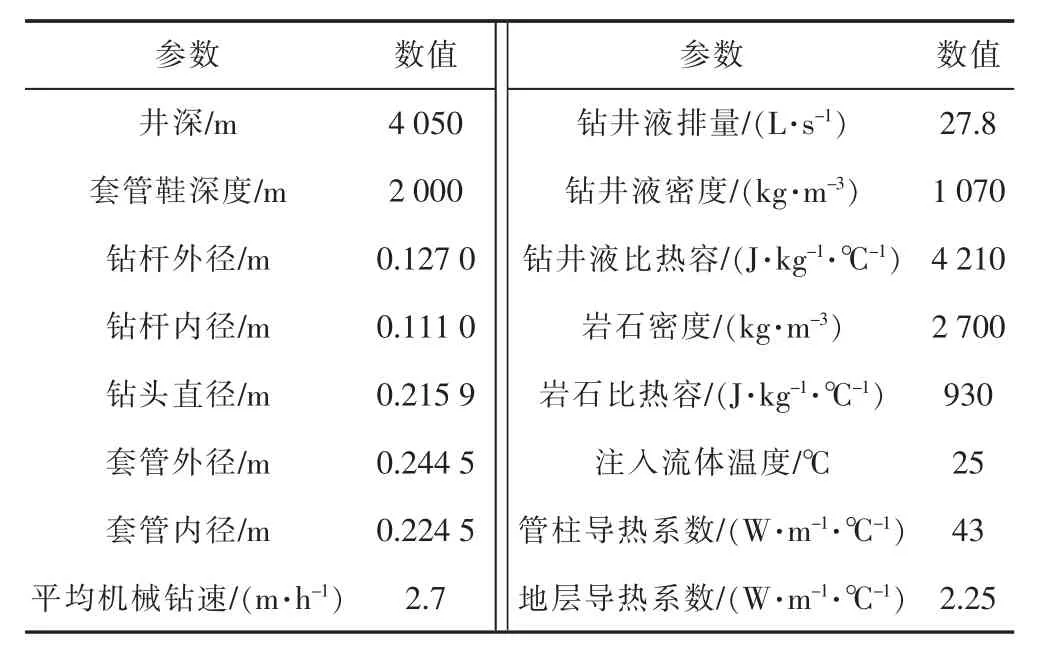
表2 N23井钻井基础数据及热物性参数

模型模拟得到的温度剖面与实测温度数据吻合较好，证明了本文模型的合理性（见图5）。在部分井段，模型计算值与实测温度数据之间存在一定差异，主要有2个原因：一是模型模拟的是循环钻进过程中的温度剖面，而实测数据是在钻进停止后测得的，该时间间隔内流体与外部发生传热，使得流体温度发生改变；二是该井2 665～3 300 m为玄武岩和砂岩夹层组合的地层，钻井过程中需要维持井壁稳定而增大钻井液密度，导致多孔砂岩层段发生钻井液漏失，降低了近井筒附近的地层温度，从而导致环空流体温度的降低。

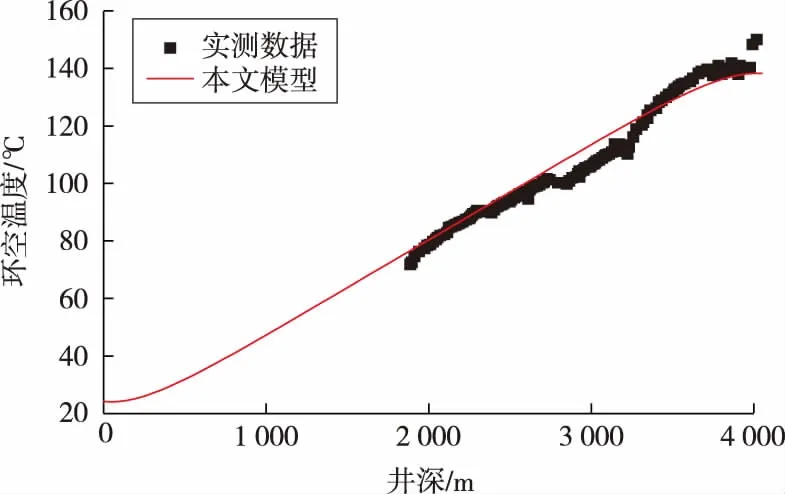
图5 N23井环空温度剖面模型计算结果与实测数据对比

5 结论

1）在传热学基本原理的基础上，充分考虑钻井过程中岩屑进入环空后对流体热学性能的影响，将井壁至原始地温位置之间的地层等效为一传热体，建立了循环钻进过程中井筒温度场的计算模型。该模型可为井筒温度场的准确计算提供理论指导。

2）对本文算例来说，当E值大于4.0时，计算结果趋于稳定，无任何不稳定问题。建议根据不同的井眼几何尺寸、钻井流体及地层特性，寻求最优的E值。

3）利用2口实测井的温度数据进行对比验证，模型模拟结果与实测温度数据吻合较好。循环钻进时，环空井底温度的模拟计算值与实测值之间的最大误差不超过7.3%，精度满足工程需要，证明了本文模型的合理性。

［1］何世明，尹成，徐壁华，等.确定注水泥与钻井过程中井内循环温度的数学模型［J］.天然气工业，2002，22（1）：42-45.

［2］KABIR C S，HASAN A R，KOUBA G E，et al.Determining circulation fluid temperature in drilling，workover，and well control operations［J］.SPE Drilling&Completion，1996，11（2）：74-79.

［3］易灿，闫振来，郭磊.井下循环温度及其影响因素的数值模拟研究［J］.石油钻探技术，2007，35（6）：47-49.

［4］席岩，柳贡慧，李军，等.页岩气井体积压裂井筒温度计算及套管强度变化分析［J］.断块油气田，2017，24（4）：561-564.

［5］罗威，廖锐全，文静，等.稠油开采双管拌热传热过程研究［J］.断块油气田，2008，15（4）：87-89.

［6］赵琥，刘文成，赵丹汇，等.深水钻井作业井下循环温度场预测［J］.中国海上油气，2017，29（3）：78-84.

［7］WARD M，GRANBERRY V，CAMPOS G，et al.A joint industry project to assess circulating temperatures in deepwater wells［J］.SPE Drilling&Completion，2003，18（2）：133-137.

［8］何世明，何平，尹成，等.井下循环温度模型及其敏感性分析［J］.西南石油学院学报，2002，24（1）：57-60.

［9］张建国.钻井循环过程中井内瞬态温度预测模型［J］.钻采工艺，2014，37（3）：5-8.

［10］陈林，孙雷，彭彩珍，等.注CO2井筒温度场分布规律模拟研究［J］.断块油气田，2009，16（6）：82-84.

［11］卢智慧，何雪芹，刘志恒，等.考虑环境因素的井筒流动温度场计算［J］.断块油气田，2016，23（5）：652-654.

［12］杨谋，孟英峰，李皋，等.钻井全过程井筒-地层瞬态传热模型［J］.石油学报，2013，34（2）：366-371.

［13］何淼，柳贡慧，李军，等.多相流全瞬态温度压力场耦合模型求解及分析［J］.石油钻探技术，2015，43（2）：25-32.

［14］HOLMES C S，SWIFT S C.Calculation of circulating mud temperatures［J］.Journal of Petroleum Technology，1970，22（6）：670-674.

［15］LI B，LI H，GUO B Y，et al.A new numerical solution to predict the temperature profile of gas-hydrate-well drilling［J］.SPE Journal，2017，22（4）：1201-1212.