时频二维低/无碰撞区跳频序列集构造
2018-04-04许成谦
许成谦, 曹 琦
(燕山大学信息科学与工程学院, 河北 秦皇岛 066004)
0 引 言
基于低/无碰撞区(low hit zone/ no hit zone,LHZ/NHZ)跳频序列的准同步组网的跳频码分多址系统是一种性能优越的跳频通信方式,与传统的跳频通信方式相比,具有更低的多址干扰以及抗多径干扰能力。LHZ/NHZ跳频序列的优劣对跳频码分多址系统的性能有着决定性的影响,所以,设计出性能良好的LHZ/NHZ跳频序列一直是研究跳频码分多址系统的重要方向之一。近年来,学者们分别在构造NHZ跳频序列[1-3]与LHZ跳频序列[4-9]方面取得了大量的研究成果。
在实际系统中,跳频信号除存在传输时延外,还可能发生频率偏移。特别是像雷达等系统在高速运动的情况下,传输信号的频率可能发生偏移,跳频序列的频隙可能移位至其他频隙,导致与其他跳频序列发生碰撞,影响通信质量。所以,有必要将只考虑时延的一维碰撞区扩展到同时考虑时延频移的二维碰撞区。文献[10]首先考虑了跳频序列包含频移的汉明相关性,用Reed-Solomon (RS)跳频序列作为实例进行分析。文献[11]设计出了基于Costas序列的跳频序列,根据实际系统可能出现的最大多普勒频移,利用循环移位法获得含有一个间隙列和一个间隙行的序列族来设计正交频分复用系统的跳频序列。文献[12]提出了时频二维无碰撞区跳频序列的概念,并推导出了此类跳频序列的理论界,设计出了时频二维无碰撞区跳频序列集。文献[13]给出了跳频序列由时频低碰撞区边长值、时频二维移位汉明相关值、频隙个数、序列的长度、序列的个数构成的理论界。文献[14]分别基于Welch Costas阵列和Golomb Costas阵列构造出了两种满足理论界的时频二维低碰撞区跳频序列集。文献[15]研究了跳频序列集时频最大周期汉明相关值的理论界,分析了Cai跳频序列集和多项式同余法构造的跳频序列集的时频二维周期汉明相关性。
本文首先证明了RS码的时频二维周期汉明自相关函数的上界,为后续的构造提供了理论基础;此后,提出了两种时频二维低/无碰撞区跳频序列集的构造方法。第一种方法基于RS码来构造时频二维周期低碰撞区跳频序列集,同时,构造出的跳频序列集也为时频二维非周期低碰撞区跳频序列集。第二种方法利用矩阵来构造时频二维非周期无碰撞区跳频序列集。
1 基本概念

(1)
式中

当s1=s2时,Hs1s1(τ,v)称为s1的时频二维周期汉明自相关函数,当s1≠s2时,Hs1s2(τ,v)称为s1和s2的时频二维周期汉明互相关函数。
下面给出时频二维非周期汉明相关函数的概念。

(2)
式中

文献[1]和文献[4]分别给出了一维汉明相关函数下具有无碰撞区和低碰撞区的跳频序列概念。下面给出时频二维汉明相关函数下具有无碰撞区和低碰撞区的跳频序列概念。

0≤τ≤TA,0≤v≤VA,(τ,v)≠(0,0)}}
(3)
0≤τ≤TA,0≤v≤VA,(τ,v)≠(0,0)}}
(4)
0≤τ≤TC,0≤v≤VC,k≠l}}
(5)
0≤τ≤TC,0≤v≤VC,k≠l}}
(6)
Lt=min{LAt,LCt},Lf=min{LAf,LCf}
(7)
若(Lt,Lf)≠(0,0),则称区间[0,LAt]×[0,LAf]为S的时频二维周期自相关低碰撞区,称区间[0,LCt]×[0,LCf]为S的时频二维周期互相关低碰撞区,称区间[0,Lt]×[0,Lf]为S的时频二维周期低碰撞区,称S为(q,L,M,Lt,Lf,Ha(S),Hc(S))时频二维周期低碰撞区跳频序列集。
为简化起见,在下面的讨论中,令Ha=Ha(S),Hc=Hc(S),Hm=max{Ha,Hc}。
特殊地,当Ha=Hc=0时,称S的低碰撞区为S的无碰撞区,用符号Z表示。此时,称区间[0,ZAt]×[0,ZAf]为S的时频二维周期自相关无碰撞区,称区间[0,ZCt]×[0,ZCf]为S的时频二维周期互相关无碰撞区,称[0,Zt]×[0,Zf]为S的时频二维周期无碰撞区,称S为(q,L,M,Zt,Zf)时频二维周期无碰撞区跳频序列集。
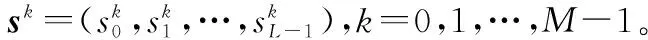
0≤τ≤TA,0≤v≤VA,(τ,v)≠(0,0)}}
(8)
0≤τ≤TA,0≤v≤VA,(τ,v)≠(0,0)}}
(9)
0≤τ≤TC,0≤v≤VC,k≠l}}
(10)
0≤τ≤TC,0≤v≤VC,k≠l}}
(11)
(12)

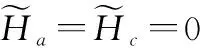
设GF(q)为q阶有限域,q=pm,p为素数,m为正整数,α是GF(q)的本原元,以多项式g(x)=(x-α)(x-α2)…(x-α2t)(t>0)生成多项式的循环码称为GF(q)上的RS码。RS码的码长为q-1,信息位数为q-2t-1。

2 性质
定理1给出了RS码码字时频二维周期汉明自相关函数的上界,即RS码码字与其时频二维移位码字碰撞次数的上界。
定理1设s为GF(q)上信息位数为b的RS码的码字,则s的时频二维周期汉明自相关函数不大于b-1,即Hss(τ,v)≤b-1。
证明
设s=(n(1),n(α),n(α2),…,n(αq-2)),则
(13)
令αi=x,根据汉明相关函数的特点知,式(13)的值等于式(14)根的个数。
n(x)-n(ατx)-v=0
(14)
因为n(x)是b-1次多项式,所以式(14)在GF(q)上最多有b-1个根,因此
Hss(τ,v)≤b-1
(15)
证毕
定理1指出RS码码字的二维汉明相关函数的上界是RS码的信息位数减1,因此为了使得码子二维汉明相关函数性小,需要采用信息位数小的RS码。

证明从S中任意选取序列sk和sl,k,l=0,1,…,M-1,其时频二维非周期汉明相关函数为
(16)

(17)


(18)
即
(19)
证毕
定理2给出了形成跳频序列集时频二维非周期无碰撞区的充分条件,从该条件可以得到判断跳频序列集时频二维非周期无碰撞区大小的有效方法。
3 构造
3.1 时频二维周期低碰撞区跳频序列集的构造方法
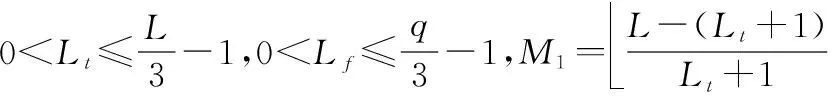
构造方法具体如下:
步骤1从C中选取M个码字sk,k=0,1,…,M-1,其中sk的信息向量为
nk=(1+k(Lf+1),α1+k(Lt+1))
(20)
式中,α是GF(q)的本原元。
步骤2将选取的每个码字看作一个跳频序列,构成跳频序列集S={sk}。其中,k=0,1,…,M-1。
定理3构造方法1所构造出的序列集S为(q,q-1,M,Lt,Lf,1,1)时频二维周期低碰撞区跳频序列集。
证明由构造方法1构造的跳频序列集频隙个数为q,序列长度为q-1,序列数目为M且M≥2,下面证明低碰撞区为[0,Lt]×[0,Lf]。
(1) 讨论自相关性
对于∀sk∈S,由构造方法1知,sk是RS码中的码字,由定理1知,对(τ,v)≠(0,0),有
Hsksk(τ,v)≤1
(21)
即S中序列的时频二维周期汉明自相关函数皆小于等于1。
(2) 讨论互相关性
设sk,sl分别是信息向量nk,nl对应的RS码码字, 其中nk=(1+k(Lf+1),α1+k(Lt+1));nl=(1+l(Lf+1),α1+l(Lt+1))(k≠l),则sk=(nk(1),nk(α),nk(α2),…,nk(αq-2)),sl=(nl(1),nl(α),nl(α2),…,nl(αq-2))∈S。
sk和sl的时频二维周期汉明互相关函数为
(22)
根据汉明相关函数的特点知,式(22)的值等于式(23)根的个数。
nk(αi)-nl(αi+τ)-v=0
(23)
令αi=x,由式(20)知式(23)为
1+k(Lf+1)+α1+k(Lt+1)x-
[1+l(Lf+1)+α1+l(Lt+1)+τx+v]=0
(24)
即
(α1+k(Lt+1)-α1+l(Lt+1)+τ)x+(k-l)(Lf+1)-v=0
(25)
当(τ,v)∈[0,Lt]×[0,Lf]时,因为1+k(Lt+1)-[1+l(Lt+1)+τ]=(k-l)(Lt+1)-τ≠0,所以α1+k(Lt+1)-α1+l(Lt+1)+τ≠0,此时式(25)为一次多项式,即式(25)在GF(q)上最多有1个根,因此
Hsksl(τ,v)≤1((τ,v)∈[0,Lt]×[0,Lf])
(26)
证毕

3.2 时频二维非周期无碰撞区跳频序列集构造
构造方法2取频隙集合F={0,1,…,q-1},其中
(27)

构造方法具体如下:

(28)
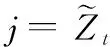
(29)
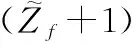
(30)
式中,T表示转置。

(31)
式中,T表示转置。


证明
(1) 证明频隙总数,序列长度的值
由式(27)和i、j、k的取值范围知,构造的跳频序列的元素取自F,因此频隙总数为

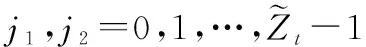


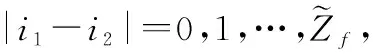
证毕
4 构造实例
4.1 构造方法1实例
设C为有限域GF(11)上的RS码,C的信息位数b=2,码长L=10,令Lt=1,Lf=1,则M1=4,M2=4,M=4。2为GF(11)上的一个本原元。从C中选取4个码字sk(k=0,1,2,3),其中,sk(k=0,1,2,3)的信息向量分别为n0=(1,2),n1=(3,23),n2=(5,25),n3=(7,27),则
s0=(3,5,9,6,0,10,8,4,7,2)
s1=(0,8,2,1,10,6,9,4,5,7)
s2=(4,3,1,8,0,6,7,9,2,10)
s3=(3,10,2,8,9,0,4,1,6,5)
将选取的每个码字sk(k=0,1,2,3)看作一个跳频序列,这4个跳频序列构成的集合S={sk}是参数为(11,10,4,1,1,1,1)的时频二维周期低碰撞区跳频序列集。
S中跳频序列的时频二维周期汉明自相关函数和互相关函数分别取值为
式中,k≠l且k,l=0,1,2,3;λ为不小于0的整数。可以看出相关函数的峰值为10,时频二维周期低碰撞区为[0,1]×[0,1]。
4.2 构造方法2实例

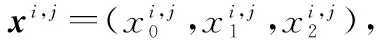
式中,i=0,1;k=0,1,2。
(2) 构造3×3阶矩阵A0、A1,表示为
(3) 构造3×3阶矩阵A2,表示为
(4) 将矩阵A0、A1、A2拼接得到矩阵A,表示为
A=[A0A1A2]=

(5) 取A矩阵每一行对应一个跳频序列sk(k=0,1,2),则所有跳频序列构成的跳频序列集S={sk}即为(19,9,3,2,1)时频二维非周期无碰撞区跳频序列集。
集合中跳频序列的时频二维非周期汉明自相关函数和互相关函数分别取值为
Hsksk(τ,v)=
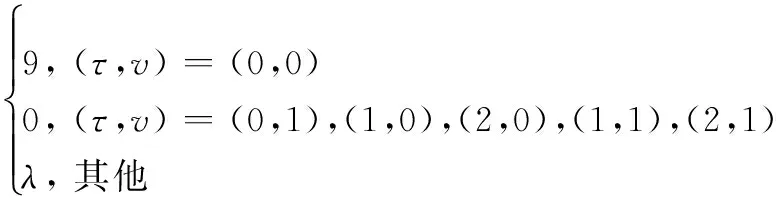
Hsksl(τ,v)=

式中,k≠l且k,l=0,1,2;λ为不小于0的整数。可以看出相关函数的峰值为9,时频二维非周期无碰撞区为[0,2]×[0,1]。
5 结 论
文献[10]以RS码为实例,分析了跳频序列在同时考虑时延和频移时的汉明相关性,但是没有给出基于RS码的低碰撞区跳频序列时频二维汉明相关函数取值的理论证明结果。本文证明了以RS码码字形成的跳频序列的时频二维周期汉明自相关函数的上界为RS码的信息位数减1。构造方法1利用RS码中一些特殊信息向量对应的码字构造出了时频二维周期(非周期)低碰撞区跳频序列集。构造方法2通过将频隙分组构成行向量,再将向量转置后拼接形成矩阵,取矩阵的行作为跳频序列,这些跳频序列构成的跳频序列集即为时频二维非周期无碰撞区跳频序列集。本文对构造方法1和构造方法2构造出的跳频序列的时频二维汉明相关性进行了严格证明,从理论上保证了这些构造方法的正确性。
参考文献:
[1] YE W X, FAN P Z. Construction of non-repeating frequency-hopping sequences with no-hit-zone[J].Electronics Letters, 2006, 42(12): 681-682.
[2] ZENG Q, PENG D, WANG X. Performance of a novel MFSK/FHMA system employing no-hit zone sequence set over rayleigh fading channel[J].IEICE Trans.on Communications,2011,94-B(2):526-532
[3] CHUNG J, HAN Y K, YANG K. No-hit-zone frequency-hopping sequence sets with optimal hamming autocorrelation[J]. IEICE Trans.on Fundamentals of Electronics, Communications and Computer Sciences, 2010, E93-A (11):2239-2244.
[4] MA W P, SUN S H. New designs of frequency hopping sequences with low hit zone[J]. Designs Codes and Cryptography, 2011,60 ( 2) :145-153.
[5] CHUNG J,YANG K. New Classes of optimal low-hit-zone frequency-hopping sequence sets by cartesian product[J]. IEEE Trans.on Information Theory, 2013, 59(1):726-732.
[6] HAN H, PENG D, PARAMPALLI U, et al. Construction of low-hit-zone frequency hopping sequences with optimal partial Hamming correlation by interleaving techniques[J]. Designs Codes and Cryptography, 2017,84(3): 401-414.
[7] LIU X, PENG D, HAN H. Low-hit-zone frequency hopping sequence sets with optimal partial Hamming correlation properties[J]. Designs, Codes and Cryptography, 2014, 73(1): 167-176.
[8] WANG C Y, PENG D Y, HAN H Y, et al. New sets of low-hit-zone frequency-hopping sequence with optimal maximum periodic partial Hamming correlation[J]. Science China Information Sciences, 2015, 36(2): 1-15.
[9] WANG C Y, PENG D Y, ZHOU L M N. New constructions of optimal frequency-hopping sequence sets with low-hit-zone[J]. International Journal of Foundations of Computer Science, 2016, 27(1): 53-66.
[10] MERSEREAU R M, SEAY T S. Multiple access frequency hopping patterns with low ambiguity[J]. IEEE Trans.on Aerospace and Electronic Systems, 1981, 17(4): 571-578.
[11] 姚建国, 王玉峰, 衡伟. Golomb Costas序列 的结构及其在OFDM系统中的应用[J]. 通信学报, 2013, 34(7): 1-13.
YAO J G, WANG Y F, HENG W. Constructions of Golomb Costas arrays and their applications in OFDM systems[J]. Journal on Communications, 2013, 34(7): 1-13.
[12] 叶文霞.无碰撞区跳频序列与准同步/消息驱动跳频通信系统研究[D].成都:西南交通大学,2011:31-40.
YE W X. Investigation of no hit zone FH sequences,quasi-synchronous and message diven FH systems[D]. Chengdu: Southwest Jiaotong University, 2011: 31-40.
[13] 许成谦,马雅楠. 时频低碰撞区跳频序列理论界的研究[J].燕山大学学报, 2017, 41(1): 68-73.
XU C Q, MA Y N. Theoretical bounds on low hit zone of time-frequency frequency hopping sequences[J].Journal of Yanshan University, 2017,41(1):68-73.
[14] 许成谦,马雅楠. 二维时频低碰撞区跳频序列集的构造[J].系统工程与电子技术,2017,39(4): 905-909.
XU C Q, MA Y N. Construction of frequency hopping sequence set with two-dimensional time-frequency low hit zone[J]. Systems Engineering and Electronics,2017, 39(4): 905-909.
[15] 刘元慧,许成谦. 两类跳频序列集时频二维汉明相关性的分析[J].系统工程与电子技术,2017,39(9):2132-2136.
LIU Y H, XU C Q. Analysis of time-frequency two-dimensional Hamming correlation of two frequency hopping sequence sets[J].Systems Engineering and Electronics,2017,39(9):2132-2136.
