分布式多无人机协同侦察目标分配研究

岳　源，屈高敏

(中国民航飞行学院， 四川 广汉　618300； 西安航空学院， 西安　710077)

随着无人机载荷能力和智能水平的进步，多无人机协同执行任务成为可能[1-4]。执行多目标侦察任务是多无人机协同应用的一个重要方向。多目标侦察任务要求无人机集群在分配目标时不重不漏且侦察价值最大。因此，多无人机在执行侦察任务中如何进行多目标的分配决策是当前无人机协同的主要课题。

文献[5]根据无人机携带传感器的侦察分辨率和目标出现时间窗约束建立了分配模型。文献[6]建立了以总飞行路程和技术数量为指标异构无人机的协同分配模型。文献[7]研究给定一组具有不同侦察载荷能力的UAV对任务场景中的多个任务区进行信息侦察。文献[8]研究了集中式协同体系下多无人机在任务执行阶段之前的侦察目标分配方法。文献[9]研究了基于时间约束的异构类型的任务处理增加了多无人机任务分配问题复杂度。文献[10]提出了利用信息确定性指标对侦察收益的大小进行衡量，并提出了一种基于时间窗机制的多无人机任务分配方法。但是这些文献没有深入分析影响无人机侦察能力的因素，并没有将这些因素对目标分配的影响考虑进去，特别是缺乏对无人机数据链容量、雷达探测能力、无人机智能水平的综合考虑。因此，本文在考虑上述因素基础上建立了针对分布式协同体系下的多无人机多目标分配策略，并采用改进分配方法的粒子群算法对模型进行求解。

1　多无人机协同体系

多无人机通过信息交互实现了集群协同。无人机集群根据控制决策机制的不同，主要分为集中式体系、分布式体系两种协同体系[11-13]。

如图1所示，集中式体系依赖于唯一的中央控制节点，一般由性能优异的无人机或地面控制站承担。中央控制节点控制着集群通信中枢，拥有集群的决策权。这种体系复杂性低，但面对突发情况响应慢，执行复杂任务效能低。特别是，承担中央控制节点的无人机故障或损毁时，整个无人机集群完成任务的质量就会极大降低。

如图2所示，分布式协同体系依赖于无人机集群自身智能水平，通过数据链进行实现控制决策。这种体系具有很高的智能水平，可以充分发挥各无人机自治水平，但对通信容量和无人机智能水平要求较高。分布式多无人机协同体系中，各无人机平台性减弱(即无人机载荷能力、飞行速度等能力的要求降低)，节点性增强(即无人机智能能力、数据链容量、传感器能力等能力要求提高)。以执行侦察任务为例：U1无人机因受损不能完成任务时，可以通过数据链将实时情况共享到无人机集群，由系统内其他无人机申请完成任务，从而提高了任务完成质量。协同工作示意图如图3。

在这个工作流程下，无人机需要拥有足够通信容量来进行大量的数据交互，需要足够的智能水平能够根据信息自主决策。就侦察任务而言，无人机传感器性能影响着任务完成的质量。同时，为了提高任务完成效率，无人机的航程也会是重要考虑因素。因此，无人机相对目标的路程、无人机探测传感器性能、无人机通信容量、无人机智能水平是影响分布式多无人机协同侦察任务完成质量的重要因素。

2　问题描述与建模

2.1　问题描述

分布式多无人机协同执行侦察任务，假设有N架无人机组成集群，设为集合U={U1,U2,…,UN}，对∀Ui∈U，〈PosU,B，S,N,v,h,I,D,Pf,Pm〉为无人机属性，PosU为无人机二维坐标位置，RU为无人机的通信容量，IU为无人机的智能水平，v为无人机巡航速度，h为无人机巡航高度，AU为无人机的雷达能力。目标集合T={T1,T2,…,TM}，M为目标数量，对∀Tj∈T，二元组〈PosT,VT〉为目标属性，PosT为目标二维坐标位置，VT为目标价值。无人机集群通过数据链共享集群各无人机信息及相应目标信息，使得集群对目标侦察优势最大。

2.2　侦察优势函数

目标分配的本质在于立足现有资源且资源配置尽可能地最优[13]。因此，应根据不同无人机的相对优势来进行任务分配。具体到侦察任务而言，分布式无人机协同体系一方面需要无人机携带的雷达载荷性能优异，另一方面依赖无人机具有较好的数据交流能力，以实现无人机集群对目标信息的掌握，因此进行对无人机目标分配时主要考虑无人机相对目标的路程优势、容量优势、雷达优势、智能优势。

2.2.1路程优势

进行任务分配时首先考虑的是无人机与目标的初始位置。为了使得分配结果最优，尽量把距离目标近的无人机分配给目标。由于集群里无人机处于不同的位置，距离不同目标的路程也不一样，那么无人机i相对与目标j的路程优势可描述为：

(1)

式(1)中：Lij指无人机i对目标j的路程优势，其值越大意味优势越大；Sij是指无人机i到目标j的距离；∑Sij是指无人机i到所有目标的距离之和。

2.2.2通信容量优势

容量优势是指当前无人机能够传输多大的数据容量。能够传输的数据容量越大，目标信息就越容易被反馈。多输入多输出技术以其大容量、高质量传输性能优势成为无线通信领域的一项重要技术。

根据文献[15]知，数据链的通信容量与带宽、天线的信噪比有关，由香龙公式可得无人机的通信容量公式为：

Cij=B·log2(1+S/N)

(2)

式(2)中：Cij表示无人机i对目标j的通信容量优势；B表示带宽；S表示无人机i传感器信号平均功率；N表示目标j背景噪声功率。

这里对通信容量优势进行归一化处理，将通信容量转化到[0,1]区间，转换方法如下(下文方法相同)：

(3)

2.2.3雷达优势

雷达优势是指当前无人机相对其他无人机雷达探测能力的优势。当前主流无人机主要搭载合成孔径雷达(SAR)，本文以SAR为研究对象建模，需要考虑无人机相对于目标的角度优势、距离优势、探测优势等。

如图4所示，无人机沿着OA方向飞行，为保证侦察效果最佳，无人机做高度为h，速度为v匀速定高飞行。无人机瞬时探测靶面长度为r，无人机与目标的俯仰角为α，SAR视场角为β时，则：

(4)

单位时间中无人机对目标的角度优势为Pa

Pa=r/v

(5)

SAR探测能力随距离的增大而减小,设雷达最大探测距离为D,目标距离雷达的距离为d，则对目标的距离优势为Pd

Pd= e-d/DZ

(6)

无人机在执行侦察时一方面取决自身的侦察能力，另一方面取决于目标的伪装程度。无人机在侦察区域中侦察到目标的能力，它可以用发现目标概率Pf、目标的伪装度Pm这两个参数表示，则对目标的探测优势为Pw

Pw=Pf·(1-Pm)

(7)

综合上述三方面的优势函数，对Pa、Pd、Pw计算结果进行归一化处理，使各分项数值处于[0,1]之间，即可得侦察优势函数为：

(8)

式(8)中，δ1+δ2+δ3=1。考虑到雷达的探测优势主要来源于距离优势，设定δ1=δ3=0.2，δ2=0.6。

2.2.4智能优势

无人机智能水平参考美国空军研究实验室的智能等级定义[16]，若无人机i智能水平处于8级，那么取无人机的智能水平Ini为0.8。无人机的智能优势即与无人机自身智能水平有关还和目标复杂度有关。可得智能优势函数为：

Iij=Ini·coj

(9)

2.2.5无人机集群目标优势函数

对上述优势函数的计算结果进行归一化处理，综上可知无人机集群任务目标函数为：

X=ω1L+ω2SA+ω3I

(10)

式(10)中：X指量化的无人机侦察优势；L指某无人机对某目标的距离优势；R指某无人机完成侦察任务的通信容量优势；A指某无人机的雷达优势(考虑到无人机的雷达侦察数据需要通过数据链来传递，数据链的通信容量决定着无人机的雷达优势是否可以发挥出来，因此要将这两个因素综合考虑)；I指某无人机的智能优势，无人机智能水平越高越容易识别目标信息；ω1、ω2、ω3为分项优势的权重(其中ω1+ω2+ω3=1，由于本模型中各分项优势重要程度接近，故设定ω1=ω2=0.35，ω3=0.3)。

2.3　协同侦察多目标分配模型

定义矩阵Xij为无人机集群对目标的侦察优势矩阵，xij表示集群第i架无人机对第j个空中目标的侦察优势指数。

(11)

定义矩阵Yj为目标的价值矩阵，yj表示第j个目标的价值指数。

(12)

综上，无人机集群对目标分配模型如下：

(13)

式(13)中，J为无人机集群对目标的侦察价值，每架无人机要么不参与分配，要么最多分配一个目标；一个目标最多分配一个无人机。

3　改进离散粒子群算法

3.1　基本算法

为了研究智能体的群体行动，人们借鉴了动物社会的群体动力学，粒子群算法通过模拟飞鸟觅食的行为来实现。通过对飞鸟位置和速度的更新来找到最优解，一般描述为：

Vij(t+1)=ωVij(t)+c1r1j(t)[yij(t)-xij(t)]+

(14)

xi(t+1)=xt(t)+vi(t+1)

(15)

式(14)中：Vij(t)指粒子i在t时刻第j维上的惯性速度；xij(t)粒子i在t时刻第j维上的维度；c1、c2为常数，分别为认知速度和社会速度的学习因子；r1j(t)、r2j(t)为[0，1]之间随机数。

3.2　改进分配方法

任务分配的求解问题中，变量的取值是离散的，所以解决非连续的优化问题要利用离散粒子群算法(DPSO算法)进行优化。在优化过程中必须进行变量的离散化：一方面需要将粒子的位置离散化，另一方面也要将更新速度离散化。粒子在选择新位置的时候，并不是在全定义域内进行选择。粒子移动的位置表示该粒子对于任务分配的结果，目标的数目也是微粒的维数，粒子的更新速度为无人机和目标之间的任务配对的变化情况[17-18]。文献[19]就运用交换子和交换序列实现了粒子群算法向离散空间的映射。文献[20-21]运用结果取整的方法，实现了位置和速度的离散化。

DPSO算法流程如图5所示。具体流程如下：

步骤1：初始化设置微粒群的规模，惯性权值，加速系数，最大允许迭代次数，生成随机的初始无人机和目标的任务配对，并计算目标评价函数的适应的值。

步骤2：就初始粒子适应度值，寻找出个体最优值、群体最优值。

步骤3：根据公式计算各微粒新的速度，并对各微粒新的速度进行限幅处理。

步骤4：根据公式计算各微粒新的位置，并对各微粒新的位置进行限幅处理。

步骤5：对每个微粒，比较其当前适应值和其个体经历过的最好适应度值，若当前适应值更优，则令当前适应值为其个体历史最好的适应度值，并保存当前位置为其个体历史最好位置。

步骤6：比较群体所有微粒的当前适应度值和全局历史最好的适应度值，若某微粒的当前适应度值更优，则令该微粒的当前适应值为全局历史最好适应度值，并保存该微粒的当前位置为全局历史最好位置。

步骤7：若满足停止条件，则搜索停止，输出搜索结果；否则，返回步骤3继续搜索。

4　仿真算例

假定飞行前任务装订为：8架无人机对8个目标进行侦察，设置粒子群种群数量为50，速度范围为[-1，1]，位置范围为[1，8]，迭代次数设定[19-21]为200，目标位置参数、无人机初始参数、无人机载荷参数分别如表1、表2、表3所示。分配结果仿真如图6所示。

通过仿真试验，可得适应度值为2.832 9。在该适应度值下，无人机集群对目标的分配策略是U1T3，U2T1，U3T2，U4T6，U5T5，U6T7，U7T8，U8T4。

表1　目标参数

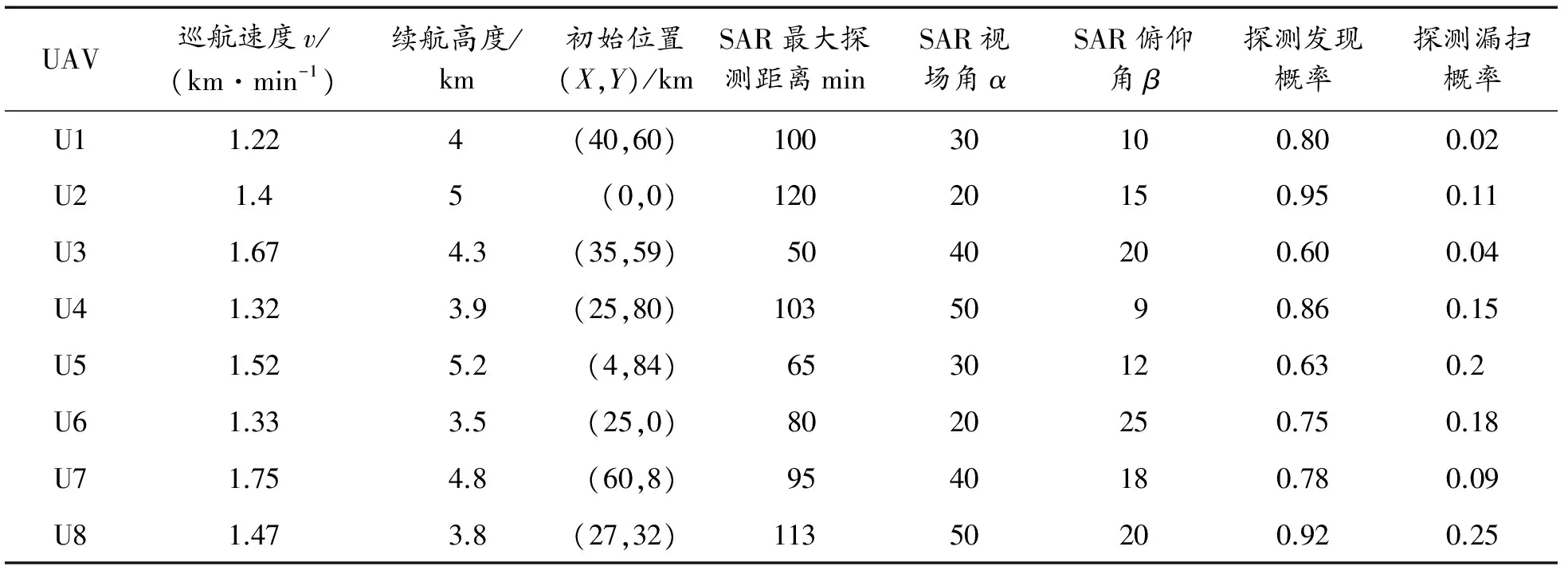
表2　无人机基本参数

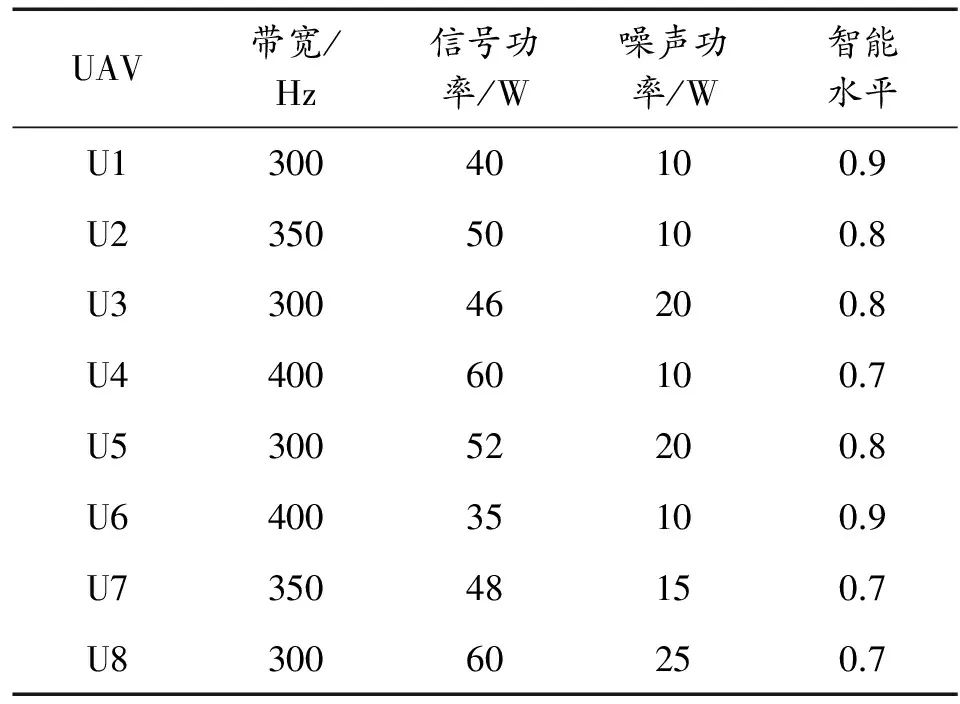
表3　无人机载荷参数

从仿真试验可以看出，离散粒子群算法在第80次迭代附近找到了最优分配方案，说明算法收敛速度比较快，能够有效地解决多约束条件下的多无人机协同任务分配问题，且目标的分配结果满足了诸多约束规则。

5　结论

本文针对分布式多无人机协同体系进行了分析，研究了影响该体系的路程、通信容量、雷达能力、智能水平四个主要因素，并在此基础上建立任务目标分配模型，贴合分布式多无人机协同的实际。针对离散粒子群算法变量不连续的问题，在考虑到执行侦察任务的基础上，提出了改进分配方法，使得分配方案有更好的实际意义，并取得了良好的收敛性。

参考文献：

[1]United States Air Force RPA vector:Vision and Enabling Concepts 2013—2038[R].Headquarters USA Air Force,17 Feb，2014.

[2]A future vision for remotely piloted aircraft:Leveraging interoperability and networked operations[R].Headquarters USA Air Force，21 Jun，2013.

[3]TIRPAK J A.Aperture:pilotless futures; modular airplanes strategic agility invisible jammers[J].Air Force Magazine， 2014(5):10-12.

[4]张洋,谭健美,朱家强.美国空军未来25年无人机系统路线图解析[J].飞航导弹,2015(1):54-57.

[5]孙健,刘慧霞,席庆彪.基于改进粒子群算法的多UAV协同侦察任务规划[J].现代电子技术,2012,35(7):12-15，18.

[6]苏菲,陈岩,沈林成.基于蚁群算法的无人机协同多任务分配[J].航空学报,2008(S1):184-191.

[7]张耀中,谢松岩,张蕾,张建东.异构型多UAV协同侦察最优化任务决策研究[J].西北工业大学学报,2017,35(3):385-392.

[8]邓启波.多无人机协同任务规划技术研究[D].北京:北京理工大学,2014.

[9]林林.基于协同机制的多无人机任务规划研究[D].北京:北京邮电大学,2013.

[10] 张蕾.多无人机协同侦察任务决策研究[D].西安:西北工业大学,2016.

[11] 黄长强,翁兴伟,王勇,等.多无人机协同作战技术[M].北京:国防工业出版社,2012.

[12] 沈林成,牛轶峰,朱华勇.多无人机自主协同控制理论与方法[M].北京:国防工业出版社,2013.

[13] 曹文静.多无人机协同体系结构研究[M].北京:国防工业出版社,2017.

[14] GALATI D G,SIMAAN M A.Effectiveness of the nash strategies in competitive multi-team target assignment problems[J].Transactions of Aerospace and Electronic systems，2007， 43(1)： 126-134.

[15] 高喜俊,陈自力.多天线结构对无人机MIMO信道容量的影响[J].航空学报,2015,36(10):3401-3410.

[16] 陈宗基,魏金钟,王英勋,周锐.无人机自主控制等级及其系统结构研究[J].航空学报,2011,32(6):1075-1083.

[17] ANDRIES P.ENGELBRECHT.计算群体智能基础[M].谭营,译.北京:清华大学出版社,2009.

[18] 高飞.MATLAB智能算法超级学习手册[M].北京:人民邮电出版社,2014.

[19] 李炜,张伟.基于粒子群算法的多无人机任务分配方法[J].控制与决策,2010(9):1359-1363，1368.

[20] 尹高扬,周绍磊,莫骏超,等.基于多目标粒子群优化的无人机协同多任务分配[J].计算机与现代化,2016(8):7-11.

[21] 王强,张安,宋志蛟.UAV协同任务分配的改进DPSO算法仿真研究[J].系统仿真学报,2014(5):1149-1155.