基于岩石物理模型的转换横波分裂在碳酸盐岩裂缝储层预测中的应用

曹占宁，李向阳*，孙绍寒，秦喜林

1 中国石油大学(北京)油气资源与工程国家重点实验室，北京 102249

2 中国石油大学(北京) CNPC物探重点实验室，北京 102249

3 中石油东方地球物理公司研发中心，涿州 072751

0 引言

裂缝型油气藏在世界已探明油气藏类型中占有重要地位，特别是我国西部地区碳酸盐岩裂缝型油气藏具有可观的油气储量。随着多波多分量地震勘探技术的不断发展，利用横波分裂技术刻画裂缝储层的发育特征成为必然趋势。

岩石物理是连接地震响应与裂缝介质参数的纽带，也是利用地震资料进行裂缝型油气藏检测的基础[1]。Bristow通过计算裂缝储层的弹性模量与泊松比研究了裂缝介质模型[2]。Schoenberg和Sayers利用线性滑动理论推导了具有水平对称轴的横向各向同性(HTI)介质的柔度矩阵[3]。Connell和Budiansky提出了自相容近似模型来探究裂缝中充填流体的等效介质的物性参数变化[4]。Xu和White针对砂泥岩储层，基于微分等效介质理论(DEM)和Gaussmann流体替换公式建立了Xu-White模型[5-6]。Xu和Payne针对碳酸盐岩储层，在Xu-White模型的基础上加入了岩石矿物组分和孔隙类型的影响，提出了Xu-Payne模型[7]。Chapman考虑了裂缝尺度对地震响应特征的影响，提出了多尺度裂缝岩石物理模型，并在此基础上分析了与频率相关的速度频散及衰减特性[8-9]。

Crampin通过多年的研究发现，广泛扩容性各向异性介质(EDA)在地下是广泛存在的，当地震波在这种裂缝定向排列的介质中传播时会产生快慢横波分裂现象[10]。通过对穿过裂缝储层的横波分裂属性的分析，可以得到大量表征裂缝储层内部结构的信息[11-12]。随后，越来越多的学者致力于研究横波分裂现象与裂缝属性之间的联系，并借此反演裂缝发育特征[13-14]。Tillostson等利用人工岩样指出横波分裂性质与岩石裂缝走向以及岩石饱含流体的性质密切相关[15]。Sayers指出横波分裂属性不仅受流体体积模量的影响，同时也和裂缝的连通性有一定关系[16]。Alford在快慢横波正交极化分裂且相互垂直的假设下，推导了二维四分量VSP横波分裂算法，并用实际横波资料进行了验证[17]。随后Lefeuvre, Winterstein和Meadows等人先后发展了传递函数法、剥层法等反演方法[18-19]。Li等利用线性变换技术提出了快慢横波分离最大化的准则，并在此基础上利用时差谱分析法求取了快慢横波时差剖面，取得了良好的效果[20-21]。肖维德等利用层剥离技术研究了多层裂缝层的横波分裂现象[22]。张建利等对三种双扫描横波分裂算法进行了对比分析，指出切向能量法最为稳定[23]。解建建重点研究了利用Alford正交旋转法进行快慢横波分离，并将其应用于新场地区实际资料，取得了较好的应用效果[24]。

本文以我国西部塔里木盆地S地区中下奥陶统鹰山组碳酸盐岩储层为研究对象，其微观结构表现为具有水平对称轴的近似垂直平行排列的宏观HTI(Horizontal Transverse Isotropic) 介质。储层具有典型的碳酸盐岩特征，裂缝等非均质体极为发育，勘探开发显示目的层具有可观的资源储量且以产气为主。本文针对研究区目的层岩石的岩石物理特征，修正Chapman模型的岩石基质部分，建立了切合实际的多尺度岩石物理模型，并在此模型基础上利用转换横波分裂属性对裂缝型储层进行了检测分析。检测结果与实际钻井资料吻合，对实际生产具有指导促进作用。

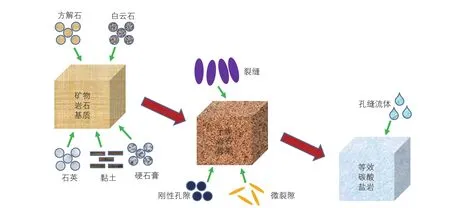
图1 碳酸盐岩等效岩石物理建模示意图Fig. 1 Carbonate rock physics model

1 方法原理

1.1 岩石物理建模

岩石物理模型是确定地震响应与裂缝介质参数的桥梁，也是利用地震资料进行裂缝型油气藏检测的基础。根据现有测井资料显示，研究区目的层岩石基质矿物主要由方解石、白云石、石英、黏土以及硬石膏组成，同时碳酸盐岩复杂的孔隙空间类型也会对岩石的等效模量产生较大影响[25-26]。本文涉及的油气储集空间主要包括圆形孔隙、微裂隙以及裂缝，同时认为各种孔缝随机均匀分布于储层中，孔缝中充填的流体主要为天然气以及矿物水。相应的岩石物理模型构建流程如图1所示，首先根据研究区岩心测井解释获得的岩石矿物基质组分，利用Voigt-Reuss-Hill平均理论计算得到矿物岩石基质的弹性模量；然后利用Chapman多尺度岩石物理理论将孔隙—微裂隙—裂缝系统加入到岩石基质中形成干燥岩石骨架，最后利用Chapman理论将天然气、水加入到岩石骨架中，计算得到等效碳酸盐岩岩石物理模型的弹性刚度矩阵。

1.1.1 Voigt-Reuss-Hill平均理论

本文利用Voigt上限和Reuss下限的Hill平均，可以计算得到含多种矿物组分的岩石基质的等效弹性刚度矩阵[27]：

其中，MV、MR分别表示岩石矿物组分的Voigt上限以及Ruess下限。

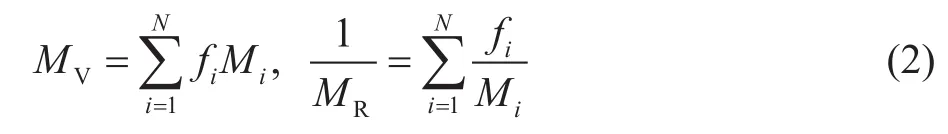
式中，fi是第i个组分的体积分数，Mi则是第i个组分的弹性模量。

1.1.2 Chapman多尺度岩石物理理论

实际裂缝型储层中通常广泛发育不同类型孔缝空间，Chapman提出了多尺度裂缝岩石物理模型，用于描述在全频带范围下的储层岩石的复杂孔隙—裂缝系统，裂缝与孔隙之间和不同孔隙之间的流体喷射流动现象[8-9]。根据Chapman多尺度裂缝岩石物理理论，等效模型的刚度张量可以表示为如下形式：

其中，C0是岩石基质的各向同性弹性刚度矩阵，分别表示来自球形孔隙、微裂隙和裂缝的附加贡献，分别乘以孔隙度φ、微裂隙密度以及裂缝密度均是拉梅系数、频率、裂缝性质和流体性质的函数。在大多数实际储层中，球形孔隙的孔隙度远大于微裂隙孔隙度，此时在地震频率范围内，式3中的微裂隙项可以忽略，从而简化模型变量，增强模型的适用性[8]。模型中流体性质的影响主要体现在三个方面的综合作用，分别是流体的体积模量、密度和颗粒尺度的弛豫时间的影响。其中，弛豫时间τm与喷射流动作用息息相关，表示流体流动时达到压力平衡所需要的弛豫时间[28]：

其中，η为流体黏滞系数，单位为Pa·s，κ为渗透率，单位为mD。

1.2 快慢横波分离

当地震波传播通过呈平行排列的垂直裂缝介质时会分裂为偏振方向近似正交的两类横波。快横波S1偏振方向平行于裂缝走向，传播速度较快；慢横波S2偏振方向平行于裂缝法向，传播速度较慢。图2是当上行转换横波传播通过呈平行排列的垂直裂缝介质时发生横波分裂的示意图，其中裂缝走向与测线方向呈θ夹角。三分量检波器的布置采用笛卡尔右手坐标系，径向分量R平行于测线方向，切向分量T垂直于测线方向，垂直方向指向读者。采集到的横波地震数据为径向分量R以及切向分量T，因此需要将R、T分量进行转换分离得到S1与S2，以便进行后续处理分析。

通过褶积模型可以更好地分析横波分裂现象，径向方向记录的地震波场R与横向方向记录的地震波场T在频率域可以表示为[21]：

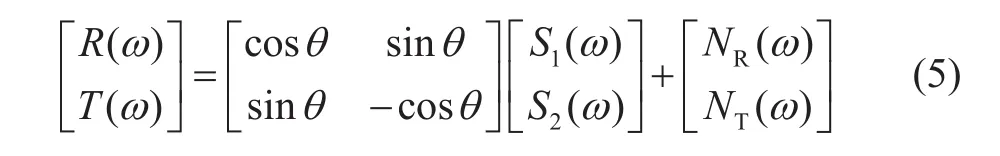
式中，ω=2πf为角频率，θ表示旋转角，NR()ω和NT()ω分别表示径向方向与横向方向的噪音分量，S1()ω和S2()ω分别表示快慢横波分量。通过计算快慢横波间的剩余误差，可以有效地将两者分离，如下式所示：

其中，∆t是快慢横波间的延迟时，将其代入式5中并进行转换，得到时间域的表示形式：

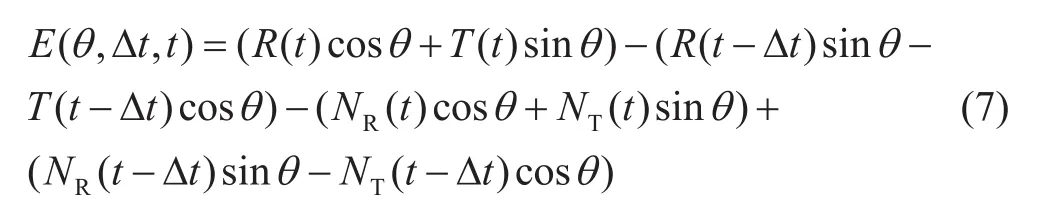
图2 裂缝走向与横波分裂示意图Fig. 2 The diagram of fracture strike direction and shear wave spliting

上式是二维矢量旋转分析的基础。对该公式进行旋转角θ与时差∆t的双参数扫描，其目标函数F(θ,∆t)可定义为：

其中，tk表示第k个采样时间。采用穷举法将每一对可能的方位角θ与时移∆t取值代入目标函数中，求得目标函数的值，比较并搜索所有计算结果中的极小值点，可以得到快横波的方位角θ和时差∆t，即可实现对快慢横波的有效分离。

2 理论模型分析

根据研究区的测井、岩芯数据，我们设计了一个三层裂缝模型以分析基于岩石物理模型的横波分裂属性特征。模型顶层为泥岩段，可以看做是各向同性层，密度为2.6 g/cm3，纵波速度为4300 m/s，横波速度为2200 m/s，层厚1000 m。奥陶统鹰山组碳酸盐岩储层是储层，储层中竖直裂缝广泛发育，近似HTI介质裂缝储层，将其设为模型的中间层，层厚500 m，孔隙度为10%，裂缝半径为1 m，裂缝纵横比为0.001，储层矿物组分及流体特征参数根据研究区实际测井资料获得，如表1所示。模型底层为基底各向同性层，密度为2.8 g/cm3，纵波速度为6000 m/s，横波速度为3150 m/s，层厚1000 m。

正演模拟的震源为25 Hz雷克子波，采用单边放炮，60道检波器接收，道间距为25 m，利用反射率法可以得到地面三分量地震记录[29]。图3与图4分别为饱含水以及饱含气时正演转换横波地震记录。两幅图中(a)、(b)分别展示了裂缝走向与测线呈45°夹角时的单炮转换横波反射道集记录，其中在零偏移距670 ms附近同相轴为裂缝储层顶界面反射，970 ms附近同相轴为裂缝储层底界面反射。选取目的层底界面反射作为研究对象，可以发现由于横波分裂现象，径向分量与切向分量存在明显的振幅差异，且由于快慢横波叠加在一起，两个分量的反射同相轴均呈现“双峰”状态，其中切向分量 “双峰”现象较为明显。利用上述双参数扫描方法进行快慢横波提取，可以分别得到饱含不同流体的快慢横波道集记录(图3c、d与图4c、d)。可以发现目的层底界面快慢横波同相轴均呈“单峰”状态，说明快慢横波得到了有效的分离。同时可以发现饱含不同流体时，快慢横波之间均具有一定的能量差异。

2.1 振幅差异分析

在各向同性介质中，根据Gassmann 理论，流体不会影响介质的剪切模量，所以介质的横波特性不会发生变化。但是在各向异性介质中，根据Brown-Korrings 理论，流体的可压缩性会严重影响横波的传播[30]。Thomsen指出地震波在裂缝介质中传播时，由于缝隙中流体压力的变化，流体会发生流动，从而影响裂缝介质的各向异性特征，进而影响横波的分裂属性[31-32]。线性滑动模型提出利用切向柔度以及法向柔度来表征裂缝系统，其中切向柔度与裂缝中充填的流体性质有关，法向柔度受流体体积模量的影响较大[33]。Chapman 提出由于不同流体的黏滞度不同，缝隙介质的慢横波特征会产生较大变化，而黏滞度主要影响流体的弛豫时间[8]。Tilloston 通过物理模型证明横波分裂特性与缝隙中充填的流体类型有极大相关性[15]。因此我们认为可以利用横波分裂的振幅特性区分具有不同体积模量与黏滞度的流体类型。

为了进一步分析饱含不同流体时的快慢横波特征，我们分别提取了裂缝密度为5%时饱含水与饱含气的目的层底界面快慢横波反射均方根振幅，并进行了统计分析。图5为目的层分别饱含水和天然气时，目的层底界面快横波与慢横波均方根振幅曲线。可以看出饱含水时，快慢横波振幅差异不大，而饱含气时，两者之间的差异较大。这是由于不同类型的流体受到地震波传播压力的影响而发生流体流动，不同的流体特征影响横波分裂特性所致。

表1 碳酸盐岩基质矿物组分特征参数Table 1 Rock physics parameters of carbonate matrix components

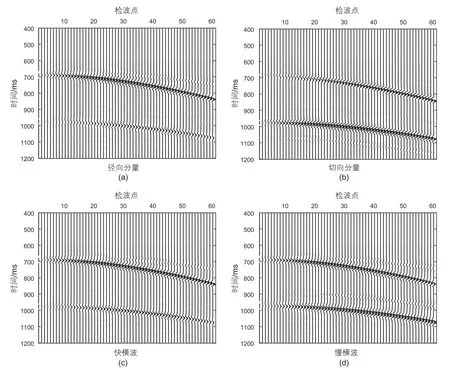
图3 饱含水时,径向分量(a)、切向分量(b)地震记录以及快慢横波((c)，(d))地震记录Fig. 3 The synthetic record of radial component (a), tangential component (b), fast shear wave (c) and slow shear wave (d)saturated with brine

为了定量说明饱含不同流体时快慢横波的均方根振幅差异，我们计算了目的层底界面的慢横波与快横波之间的振幅差值以及两者之间的比值，如图6所示。可以发现，饱含水时，近偏移距的慢横波振幅小于快横波振幅，随着偏移距的增大，两者之间的差异由负值变为正值，其比值变化范围在80%～120%；而饱含气时，慢横波振幅一直小于快横波振幅，且随着偏移距的增大，两者之间的差异逐渐增大，其比值逐渐减小，近偏移距比值在60%左右，此后逐渐减小。说明快慢横波的反射振幅比值对流体类型较为敏感，当振幅比值小于60%时，裂缝中充填天然气；当比值大于70%时，裂缝中含水的可能性较大。

2.2 延迟时间分析

同时为了验证裂缝密度对快慢横波分裂性质的影响，选取不同裂缝密度进行横波分裂分析。图7分别为目的层底界面快横波反射时间与慢横波反射时间随裂缝密度的变化，可以看到，随着裂缝密度的增大，快横波的反射时间基本不变；而慢横波的反射时间随着裂缝密度的增大而增大，且反射时间增量与偏移距大小无关。说明裂缝密度的改变不会对沿裂缝走向传播的快横波反射旅行时造成影响，但是对沿裂缝法向传播的慢横波反射旅行时影响较大，从而验证说明了利用快慢横波之间的延迟时间可以判断裂缝密度的大小，延迟时间越大，裂缝发育密度越大。

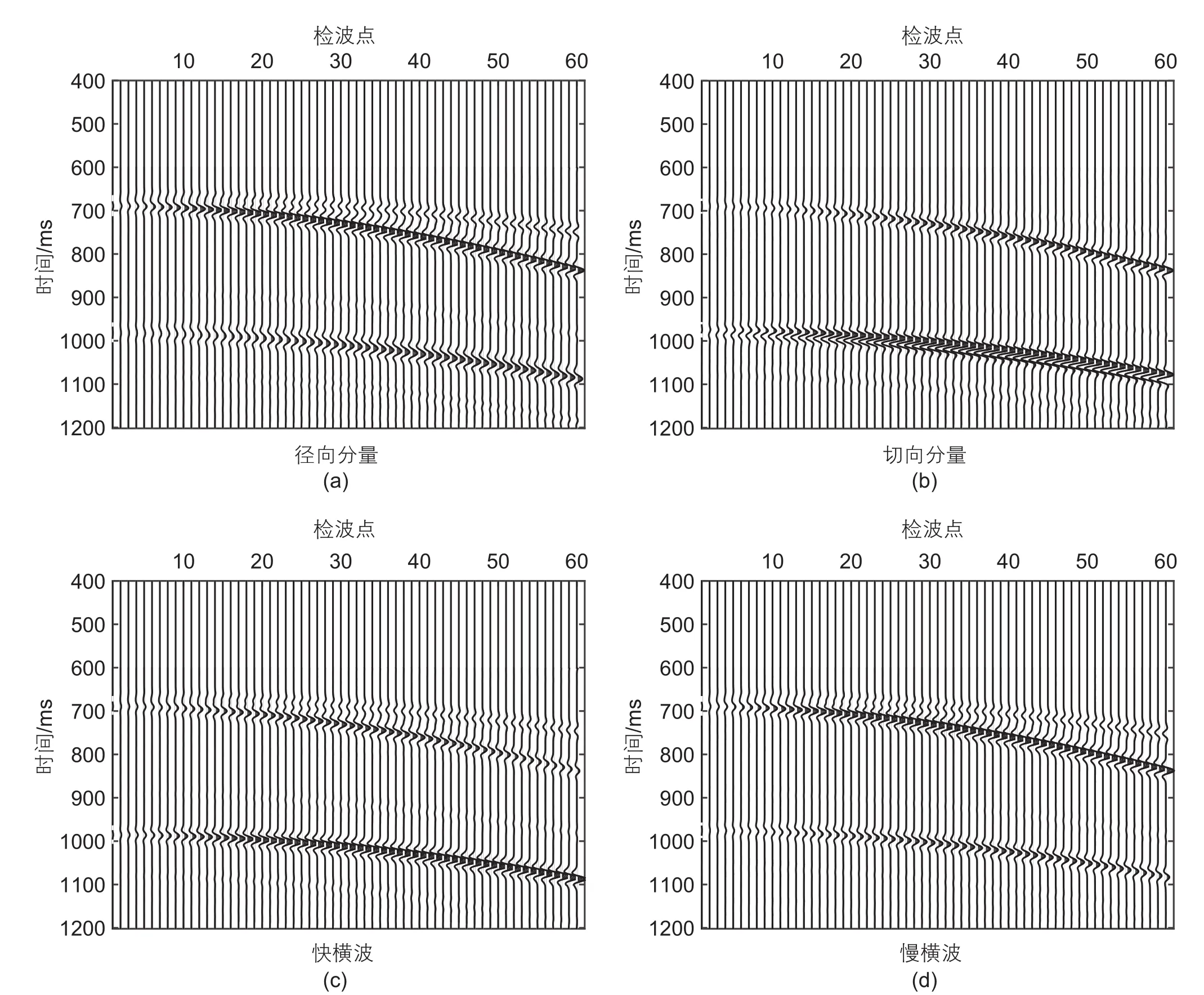
图4 饱含气时,径向分量(a)、切向分量(b)地震记录以及快慢横波((c)，(d))地震记录Fig. 4 The synthetic record of radial component (a), tangential component (b), fast shear wave (c) and slow shear wave (d) saturated with gas

图5 饱含水(a)与饱含气(b)时，目的层底界面快横波与慢横波均方根振幅曲线Fig. 5 The RMS amplitude curves of fast shear wave and slow shear wave of the bottom of fracture layer saturated with brine (a) and gas (b)

图6 饱含不同流体时，目的层底界面慢横波与快横波的均方根振幅之差(a)与均方根振幅之比(b)Fig. 6 The RMS amplitude difference (a) and ratio (b) of fast shear wave at the bottom of fracture layer saturated with different fluid

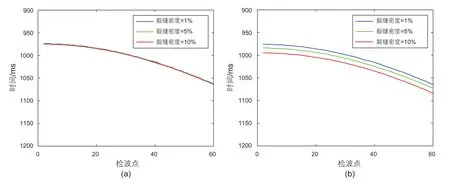
图7 不同裂缝密度时，目的层底界面快横波反射时间(a)与慢横波反射时间(b)随偏移距的变化Fig. 7 The travel time curves of fast shear wave (a) and slow shear wave (b) of the bottom of fracture layer with different fracture densities

基于以上数值模拟分析，我们认为转换横波的分裂属性可以作为研究区碳酸盐岩天然气储层预测的重要依据。通常认为在研究区块中裂缝密度大且饱含气的储层为目标储层，因此可以结合利用快慢横波之间的延迟时间与反射振幅能量差异属性进行含气储层预测。

3 实例分析

依据前文数值模拟分析，笔者将快慢横波之间的延迟时间与反射振幅能量差异分析应用于实际多波地震采集资料中，进行实际裂缝型油气藏检测。研究区为我国西部塔里木盆地S地区中下奥陶统鹰山组碳酸盐岩储层。多年的勘探开发表明，该区广泛发育高角度裂缝等各向异性地质体，呈现宏观HTI 介质特征，天然气储量丰富，持续勘探具有巨大的资源基础。为提高转换横波资料的可靠性，前期我们已经对横波数据进行了静校正、保幅去噪、吸收补偿、反褶积率等一系列预处理工作，文中通过多波处理软件提取了转换波地震资料的横波分裂参数。

图8为目的层快慢横波之间的反射延迟时间平面分布图，不同颜色表示快慢横波之间的延迟时间不同，红色代表较大的延迟时间，蓝色代表较小的延迟时间。从图中可以看出，研究区内时间延迟的变化范围为25～35 ms。研究区中东部时间延迟成条带状北西—东南向分布，且西南部时间延迟明显大于中东部，说明研究区西南部(图中红色三角形区域)裂缝集中发育，密度较大。

图9为目的层段60 ms时窗内慢横波反射能量与快横波反射能量的比值差异，不同颜色表示快慢横波之间的反射振幅比值不同，红色代表较大的比值，蓝色代表较小的比值。可以发现，研究区能量比值的变化范围在0.2～1。西南部能量比值较低，中部地区比值间隔分布，东北部比值接近于1。说明西南部储层(图中红色椭圆形区域)以含气为主，而东北部含水比例较高。对比多波工区内钻井的油气显示数据(表2)，可以发现大部分井都位于反射振幅比值的低值区域，而高值区域无井位分布。

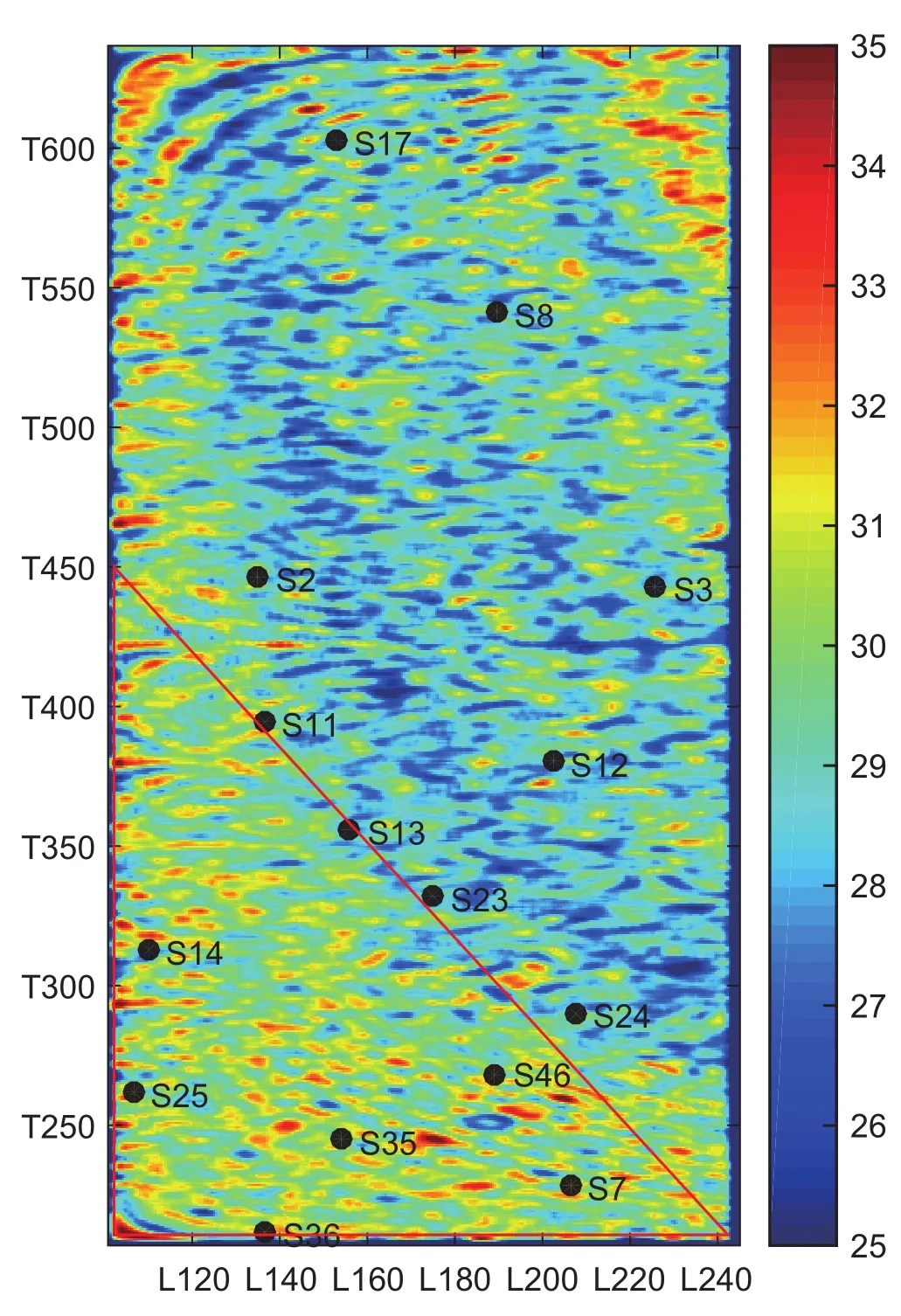
图8 快慢横波之间延迟时间分布图Fig. 8 The map of time delay between fast and slow shear wave

将延迟时间、反射振幅比与研究区内已知开发井的相对产能数据(图10)进行对比分析，可以发现S14、S35、S25井天然气累计产量较高，位于时间延迟大且能量比值低的区域，说明该区域裂缝十分发育且以含气为主，具有较大的勘探开发潜力；S23、S2井累计采水较多，位于时间延迟过渡带且能量比值较低的区域，说明该区域裂缝发育但缝隙填充流体主要为水；S8、S17井目的层为干层，位于时间延迟小且能量比值高的区域，说明该区域裂缝不发育，流体填充较少。统计分析研究区延迟时间(图8)、振幅比值(图9)、钻井结果(表2)以及累计产能(图10)，可以发现虽然由于目标储层埋深较大，快慢横波数据信噪比较低，预测结果存在一定误差，但是预测结果与钻井及试采数据大体吻合，表明了预测方法的有效性以及预测结果的可靠性。

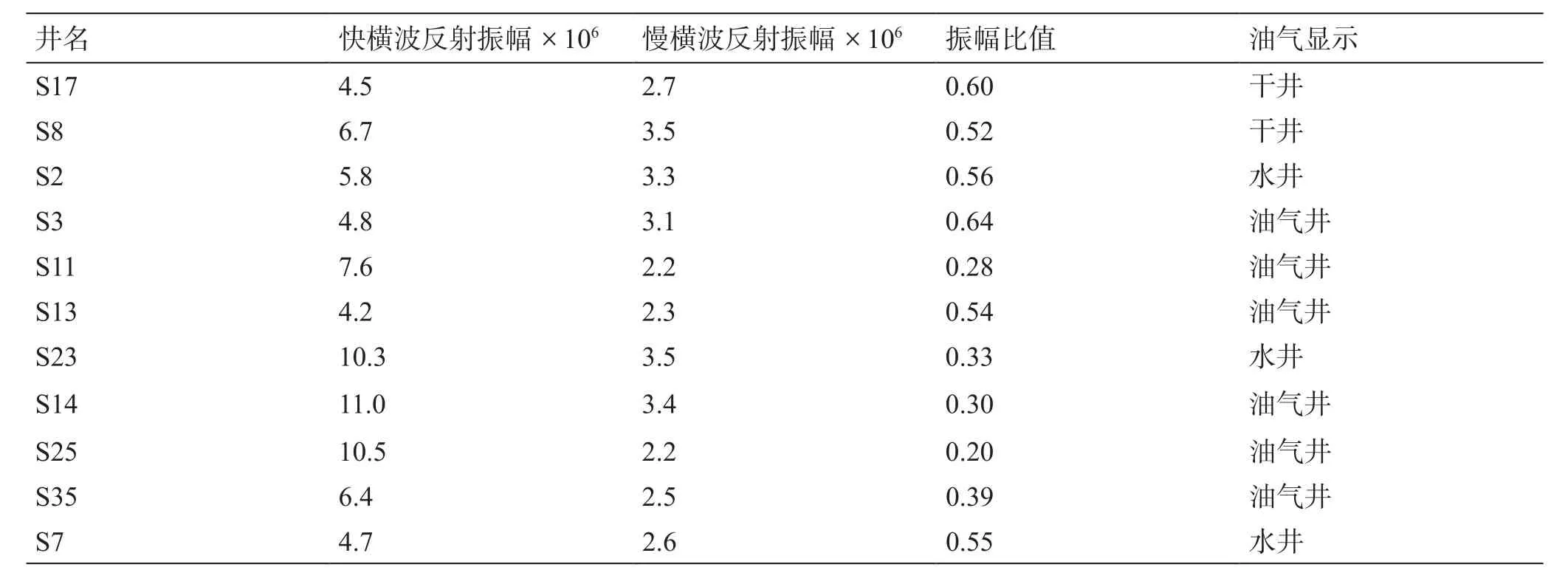
表2 反射能量与钻井结果对比Table 2 The comparison of re flected energy and drilling data

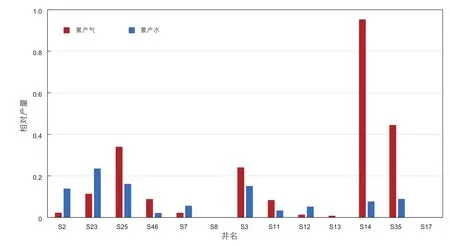
图10 研究区开发井相对累计产能对比图Fig. 10 The relative accumulative capacity of development wells in the study area

4 结论

本文提出的裂缝储层检测方法充分利用了Chapman模型可以描述多尺度孔缝空间的优势，并与VRH平均相结合，修正了岩石基质矿物组分构成，建立了更加切合实际的岩石物理模型，为横波分裂属性分析提供了理论基础。模型和实际数据的横波分裂属性分析表明，饱含水时快慢横波之间的能量差异较小，而饱含气时两者之间能量差异较大，同时验证了快慢横波之间的延迟时间随着裂缝的发育密度增大而增大。因此，我们认为快慢横波延迟时间较大且能量差异明显的区域为有利含气储层。实际应用结果与钻井及试生产结果一致，进一步表明了预测结果的可靠性以及利用本文方法进行碳酸盐岩含气储层预测的有效性与实用性。

[1] 徐胜峰, 李勇根, 曹宏, 等. 地震岩石物理研究概述[J]. 地球物理学进展, 2009, 24 (02): 680-691. [XU S F, LI Y G, CAO H, et al.The overview of seismic rock physics research [J]. Progress in Geophysics, 2009, 24 (02): 680-691.]

[2] BRISTOW J R. Microcracks and the static and dynamic elastic constants of annealed and heavily cold-worked metals [J]. British Journal of Applied Physics, 1960, 11 (2): 81-85.

[3] SCHOENBERG M, SAYERS C M. Seismic anisotropy of fractured rock [J]. Geophysics, 1995, 60 (1): 204-211.

[4] O'CONNELL R J, BUDIANSKY B. Seismic velocities in dry and saturated cracked solids [J]. Journal of Geophysical Research Atmospheres, 1974, 79 (35): 5412-5426.

[5] XU S, WHITE R E. A new velocity model for clay-sand mixtures [J]. Geophysical Prospecting, 1995, 43 (1): 91-118.

[6] XU S, WHITE R E. A physical model for shear-wave velocity prediction [J]. Geophysical Prospecting, 1996, 44 (4): 687-717.

[7] XU S, PAYNE M A. Modeling elastic properties in carbonate rocks [J]. Leading Edge, 2009, 28 (1): 66-74.

[8] CHAPMAN M. Frequency-dependent anisotropy due to meso-scale fractures in the presence of equant porosity [J]. Geophysical Prospecting, 2003, 51 (5): 369-379.

[9] CHAPMAN M. Modeling the effect of multiple sets of mesoscale fractures in porous rock on frequency-dependent anisotropy [J].Geophysics, 2009, 74 (6): 97-103.

[10] CRAMPIN S. A review of wave motion in anisotropic and cracked elastic media [J] .Wave Motion, 1981, 3 (4): 343-391.

[11] MARTIN M A. Shear-wave birefringence: A new tool for evaluating fractured reservoirs [J]. Leading Edge, 1987, 6 (10): 22-28.

[12] CRAMPIN S. Evaluation of anisotropy by shear-wave splitting [J]. Geophysics 1985, 50 (1): 142–152.

[13] QUINTAL B, JÄNICKE R, RUBINO J, et al. Sensitivity of S-wave attenuation to the connectivity of fractures in fluid-saturated rocks[J]. Geophysics, 2014, 79 (5): 15–24.

[14] FOORD G, VERDON J, KENDALL J. Seismic characterization of fracture compliance in the field using P- and S-wave sources [J].Geophysical Journal International. 2015, 203 (3): 1726–1737.

[15] TILLOTSON P, CHAPMAN M, BEST A, et al. Observations of fluid-dependent shear-wave splitting in synthetic porous rocks with aligned penny-shaped fractures [J]. Geophysical Prospecting, 2011, 59 (1): 111–119.

[16] SAYER C M. Fluid-dependent shear-wave splitting in fractured media [J]. Geophysical Prospecting, 2015, 50 (4): 393–401.

[17] ALFORD R M. Shear data in the presence of azimuthal anisotropy [C]. 56th Annual SEG Meeting Expanded Abstracts, Dilley, Texas,1986.

[18] LEFEUVRE F. Propagator matrix and layer stripping methods: A comparison of shear-wave birefringence detection on two data sets from railroad gap and Lost Hills fields [C]. 61st Annual SEG Meeting Expanded Abstracts, Houston, Texas, USA, 1991.

[19] WINTERSTEIN D F, MEADOWS M A. Shear-wave polarizations and subsurface stress directions at Lost Hills Field [J]. Geophysics,1991, 56 (9): 1331-1348.

[20] LI X, CRAMPIN S. Linear-transform techniques for analyzing shear-wave splitting in four-component seismic data [J]. Geophysics,1993, 58 (2): 240-256.

[21] 李向阳. 一种检测油气储层中裂缝发育程度的方法及装置[P]. 中国: CN103076632A, 2014-05-01. [LI X Y. A method and device for detecting the development degree of fracture in oil and gas reservoirs [P].China: CN103076632A, 2014-05-01.]

[22] 肖维德, 徐天吉, 丁蔚楠. 利用转换横波层剥离分析技术检测裂缝[J]. 石油地球物理勘探, 2013, 48 (06): 966-971. [XIAO W D,XU T J, DING W N. Fracture detection with layer-stripping of PS-wave splitting [J]. Petroleum Geophysical Prospecting. 2013, 48 (06):966-971.]

[23] 张建利, 王赟, 刘志斌, 等. 三种双扫描横波分裂算法在裂缝探测中的应用研究[J]. 石油地球物理勘探，2017, 52 (01): 105-113. [ZHANG J L, WANG Y, LIU Z B, et al. Application of three kinds of double scanning shear wave splitting algorithm in fracture detection [J]. Petroleum Geophysical Prospecting, 2017, 52 (01): 105-113.]

[24] 解建建. 基于横波分裂分析的裂缝检测方法研究及应用 [D]. 成都: 成都理工大学, 2011. [XIE J J. The research and application of fracture detection methods based on shear wave splitting [D]. Chengdu: Chengdu University of Technology, 2011.]

[25] KUMAR M, HAN D H. Pore shape effect on elastic properties of carbonate rocks [C]. 75th Annual SEG Meeting Expanded Abstracts,Houston, Texas, USA, 2005.

[26] LUCIA. Rock-fabric/petrophysical classi fication of carbonate pore space for reservoir characterization [J]. AAPG Bulletin, 1995, 79 (9):1275-1300.

[27] MAVKO G, MUKERJI T, DVORKIN J. The rock physics handbook: Tools for seismic analysis of porous media [M]. Cambridge:Cambridge University Press, 2009.

[28] AL-HARRASI O H, KENDALL J M, CHAPMAN M. Fracture characterization using frequency-dependent shear wave anisotropy analysis of microseismic data [J]. Geophysical Journal International, 2011, 185 (2): 1059-1070.

[29] 寻浩, 董敏煜, 牟永光. 各向异性介质中反射率法波场模拟及体波辐射图案[J]. 石油地球物理勘探, 1997, 32 (5): 605-614. [XUN H, DONG M Y, MOU Y G. Wave field simulation using re flectivity method and body-wave radiation patterns in anisotropic media [J].Oil Geophysical Prospecting, 1997, 32 (5): 605-614.]

[30] BROWN R J S, KORRINGA J. On the dependence of the elastic properties of a porous rock on the compressibility of the pore fluid [J].Geophysics, 1975, 40 (4): 608-616.

[31] THOMSEN L. Elastic anisotropy due to aligned cracks in porous rock [J]. Geophysical Prospecting, 1995, 43: 805–829.

[32] ZATSEPIN S V, CRAMPIN S. Modelling the compliance of crustal rock—I. Response of shear-wave splitting to differential stress [J].Geophysical Journal International, 1997, 129: 477–494.

[33] SCHOENBERG M, DOUMA J. Elastic wave propagation in media with parallel fractures and aligned cracks [J]. Geophysical Prospecting, 1988, 36: 571–590.