基于AHP和VPRS的输变电施工风险灰色综合评价研究
2018-04-03秦伟
秦 伟
(广州供电局有限公司,广东 广州 510620)
据国家能源局统计数据,2017年上半年,全国发生电力人身伤亡责任事故29起,死亡(失踪)37人,重伤1人。其中,电力建设人身伤亡事故9起,死亡(失踪)17人,造成重大社会影响和人身财产损失。电力建设伤亡事故主要集中在触电、高处坠落、起重机械伤害、物体打击和坍塌等事故[1-2]。面对严峻的电力建设安全生产形势,要实现安全生产,需全面系统分析输变电工程安全生产影响因素与风险评价方法。因此,探索出简单有效的输变电工程安全评价方法显得尤为重要。
国内施工安全评价研究主要集中在建筑施工安全上,而输变电工程施工安全风险评价研究相对较少。在风险评价指标体系方面,黄世国等[3]从人、机和环境3个维度构建了施工安全评价指标体系。张健等[4]用分叉树对施工现场进行分析,结合层次分析法确定指标权重。王朋等[5]在构建三级施工安全风险指标基础上,用变精度粗糙集与层次分析法确定指标权重。在施工风险评价方面,倪明杨[6]利用物元理论构建施工风险评价模型。林陵娜等[7]采用调查研究法筛选施工安全关键因素,构建基于系统动力学理论的施工安全状态识别模型。黄国忠等[8]针对施工现场安全因素的灰色特性,建立灰色欧几里德理论安全评价模型。杨莉琼等[9]对施工安全进行定量分析,构建二元决策图安全风险评价模型。翟越等[10]用BIM虚拟施工技术构建多维数字化施工安全评价模型。王友国等[11]在大型工程项目中用Gray-Shapley理论构建施工安全评价模型。安磊等[12]构建故障树风险评价模型。姚俊伟等[13]用层次分析法对输变电工程进行安全性后评价。潘华等[14]建立输变电工程三角模糊综合评价模型。高杨杨等[15]结合三角模糊数,构建输变电工程安全评价云模型。
上述施工安全风险评价模型较少考虑施工安全风险较强的非线性、模糊性及定性指标偏多等问题。鉴于此,笔者结合变精度粗糙集(VPRS)与层次分析法(AHP)确定指标权重,运用灰色系统理论构建输变电工程施工安全风险多层次灰色评价模型;并结合输变电工程施工实例对安全风险进行综合分析评价,以验证模型的科学合理和可操作性。
1 评价指标体系的建立
输变电工程施工现场条件复杂多变,各安全风险因素相互影响,评价指标的合理选择直接影响施工安全风险评价的科学性与准确性。施工现场具有人员流动性大,施工技术条件和环境复杂,露天作业、高空作业、特种作业多等特性。在大量文献资料研究的基础上,结合施工实例和电力施工安全检查标准,遵循安全风险的全面系统性、层次科学性和可操作性原则,采用事故致因与人机工程学理论分别从人员因素、设备因素、技术因素、环境因素和管理因素5个维度对施工安全风险因素进行归纳总结,构建输变电工程施工安全风险评价指标体系,如图1所示。
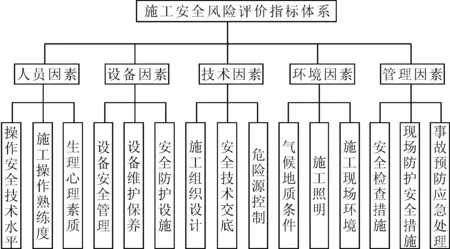
图1 输变电工程施工安全风险评价指标体系
2 指标权重的确定
2.1 变精度粗糙集理论
变精度粗糙集是在粗糙集上经过预置近似精度因子β(0.5<β≤1)扩充得到,有利于消除施工安全指标在专家打分决策时的分类误差,有效解决属性间不确定性关系或无函数的数据分类问题。设条件属性集为C,决策属性集为D,有C,D⊆A,A为有限属性集。当所有评分对象集合为U时,若集合Z与集合P分别隶属于集合U与集合C,则可将Z划分3个区间:
(1)
(2)
(3)
其中,E(P)为基于P的条件类,表示等价类集合。令打分的对象(施工项目)数量为card(U),则P相对于D的变精度粗糙集分类质量(quality of classification)QoC为:
(4)
QoC的数值在一定程度上体现了条件属性间的重要性,可以用来构建判断矩阵以确定施工风险指标在施工安全中的重要度。γβ(P,D)为P在正确分类率β条件下,划入决策属性D的数量,其数值大小同D对于P的重要度成正比。因此,QoC可用于表示条件类P相对决策属性D的重要性。
2.2 变精度粗糙集模型
针对施工安全评价指标,采用变精度粗糙集理论构建指标权重确定模型。令Pi表示指标体系中第i(i=1,2,…,n)个指标,且各指标间相对独立;群决策Pki相对于Dk的重要性可以通过专家对各样本及相关指标打分得到,即:
(5)
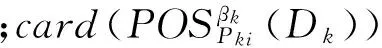
构造层次分析的矩阵集合B={B1,B2,…,Bm},其中Bk为判断矩阵,取决于第k个专家的打分。
(6)
其中,bkij为第k个专家确定出的指标体系Pi相对于Pj的重要程度,即:
由于bkij×bkjh=bkih,所以Bk是完全一致判断矩阵。变精度粗糙集计算过程中的判断结果可以有效解决判断矩阵不一致的问题。条件属性Pki特征值可以通过几何平均法得到:
(8)
(9)
归一化处理后可得出判断矩阵Bk中指标权向量为:
(10)
(11)
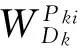
在群决策表的基础上,结合层次分析法与变精度粗糙集理论对输变电施工安全指标从主观和客观两方面进行评价,设对应权重分别为Ok和Sk。B表示m个专家判断矩阵的集合;Bk跟其他判断矩阵之间相似性反映出第k个专家的客观权重大小,相似性越低则专家权重越低。
bkj=(bk1j,bk2j,…,bknj)
(12)
vec(Bk)=(bk1,bk2,…,bkn)
(13)
那么专家i*与专家j*之间的相似性定义为:
(14)
其中,0 (15) 因此,将第k个专家的客观权重定义为: (16) (17) 灰色系统研究的是不确定性以及“部分信息缺失”的小样本数据系统。多层次灰色评价模型综合定量计算与定性分析,能有效解决系统信息数据缺乏和定性指标偏多的问题,采用变精度粗糙集模型确定指标权重,再运用灰色系统理论来确定安全风险指标的白化权矩阵和白化权向量,最后对施工安全风险进行综合评价。 对于定性指标采用专家打分法进行评分,评分值为1~5。然后采用集对分析模型确定施工安全指标权重,其权重集用A来表示,即一级指标权重集为A=(a1,a2,a3,a4,a5),二级指标权重集为Al=(Al1,Al2,…,Aln),其中l=1,2,…,5。 (1)建立评价样本矩阵。有P位专家对施工安全定性评价指标打分,且第W位专家对指标Pij的打分为dijw,则构建评价样本矩阵为D。 (18) (2)确定评价对象灰类。根据评价等级将评价灰类划分为5类,相应灰数和白化权函数为: 第一灰类“低风险”,灰数设定为⊗1∈[0,1,2],对应白化函数f1(dijw)的表达式为: (19) 第二灰类“较低风险”,灰数设定为⊗2∈[0,2,4],对应白化函数f2(dijw)的表达式为: (20) 第三灰类“中等风险”,灰数设定为⊗3∈[0,3,6],对应白化函数f3(dijw)的表达式为: (21) 第四灰类“较高风险”,灰数设定为⊗4∈[0,4,8],对应白化函数f4(dijw)的表达式为: (22) 第五灰类“高风险”,灰数设定为⊗5∈[0,5,10],对应白化函数f5(dijw)的表达式为: (23) (3)灰色评价系数计算。定性指标Pij的第e个评价灰类的灰色评价系数xije为: (24) 那么评价项目各个评价灰类的总灰色评价系数xij为: (25) (4)确定指标灰色评价权向量。记评价指标Pij的第e个灰色评价权为rije,则: rije=xije/xij (26) 那么评价指标Pij的灰色评价权向量rij为: rij=(rij1,rij2,rij3,rij4,rij5) (27) 全部指标灰色评价权矩阵Rk为: (1)设Gk表示指标Pk属于各灰类灰色评价权向量,gke(e=1,2,…,5)表示指标Pk的第e个灰类的灰色评价权,则有: Gk=Ak·Rk=(gk1,gk2,…,gk5) (29) (2)依据Pk的综合评价结果Gk得到Pk属于各评价灰类灰色评价权矩阵R: G=A·R=(g1,g2,…,g5) (30) 按最大隶属度原则,ge所得最大值即为Pk的评价灰类。为完善评价结果,将低风险、较低风险、中等风险、较高风险、高风险5个风险等级赋值为1、2、3、4、5,得到各评价灰类等级值化向量C=(1,2,3,4,5),最终得到施工安全风险评价等级Z为: Z=G×CT (31) 广东某220 kV输变电工程本期新建主变压器2×240 MVA,规划220 kV出线4回,110 kV出线6回,10 kV出线20回, 无功补偿容量电容器2×(6×10 020) kvar,主接线采用双母线接线。根据所构建的输变电工程施工安全评价指标体系,邀请5位经验丰富的电力建设工程专家对施工安全风险指标进行打分,具体评分值如表1所示。 表1 施工安全风险指标评价值 根据变精度粗糙集模型确定指标权重的步骤,先由专家组现场对施工安全指标进行打分,依据打分值构建要素评价决策表,其中近似精度因子β取值0.2,经计算得到一级指标权重A=(0.272 8,0.150 5,0.196 9,0.167 5,0.222 2),详细计算过程可参考文献[5]。 同理,计算得到施工安全二级指标权重,分别为A1=(0.364 0,0.323 3,0.232 8);A2=(0.385 4,0.320 9,0.340 9);A3=(0.362 1,0.331 1,0.360 1);A4=(0.310 4,0.323 6,0.347 5);A5=(0.374 0,0.275 0,0.340 2)。 根据专家评分数据和多层次灰色评价模型的计算步骤,得到施工安全风险指标的灰色评价权向量矩阵R: 二级灰色综合评价: G1=A1×R1=(0.364 0,0.323 3,0.232 8)× (0.047 4,0.168 9,0.228 5,0.250 0,0.225 2) G2=A2×R2= (0.000 0,0.199 0,0.313 5,0.309 2,0.225 5) G3=A3×R3= (0.028 7,0.243 1,0.313 5,0.260 0,0.208 0) G4=A4×R4= (0.052 7,0.202 6,0.281 5,0.247 0,0.197 6) G5=A5×R5= (0.117 8,0.275 1,0.239 2,0.198 4,0.158 7) 一级灰色综合评价: G=A×R= (0.056 3,0.224 3,0.272 6,0.249 8,0.201 8) Z=G×CT=3.33 在输变电工程施工安全风险五大影响因素中,从一级指标权重角度来分析,可以看出人员因素最为重要,说明在施工中要重视人的安全影响因素。结合变精度粗糙集与层次分析法确定一级指标重要度排序结果为:人员因素>管理因素>技术因素>环境因素>设备因素,与文献[9]一致,验证了权重模型的科学性与有效性。 依据风险等级划分,根据评价结果得出输变电施工安全风险,风险评价结果为3.33主要集中在中等风险。由此可以判断该输变电工程项目施工安全风险等级为中等偏高,施工过程中应加强安全风险控制,重点加强施工现场人员管控,做好安全交底、技术交底和任务交底,防范高空作业和人员触电事件,保障输变电工程施工安全。 施工安全风险评价指标权重的确定,结合了变精度粗糙集与层次分析法,使施工安全指标权重更加贴合实际,提高了输变电工程施工安全风险评价结果的准确可靠性。笔者综合变精度粗糙集与层次分析法,利用灰色多层次综合评价模型,对输变电工程施工项目实例进行评价分析,得出项目施工安全风险等级为中等偏高,人员因素对施工安全影响最大,验证了模型的可操作性与科学合理性。 参考文献: [1]李伟民,沈辉,程淼生,等.输变电工程重大危险源风险及应急管理[J].电力与能源,2011,32(3):247-250. [2]冯凯梁.建筑施工危险源分类研究综述及应用[J].武汉理工大学学报(信息与管理工程版),2017,39(1):41-44. [3]黄世国,袁晓.建筑施工安全综合评价体系的研究与应用[J].西南大学学报(自然科学版),2012,34(7):130-135. [4]张健,王晓新,蔡亮,等.建筑施工现场安全评价指标与权重值确立[J].沈阳建筑大学学报(自然科学版),2012,28(3):485-490. [5]王朋,方向,刘婷,等.基于AHP和VPRS输变电施工风险指标及权重研究[J].武汉理工大学学报(信息与管理工程版),2016,38(5):557-560. [6]倪明杨.基于物元分析理论高层建筑施工安全风险评估[J].武汉理工大学学报(信息与管理工程版),2016,38(3):293-296. [7]林陵娜,苏振民,王先华.基于系统动力学的建筑施工项目安全状态识别模型构建[J].中国安全生产科学技术,2011,7(12):80-86. [8]黄国忠,吴忠广,杨灿生,等.基于灰色欧几里德理论的建筑施工安全评价模型[J].北京科技大学学报,2011,33(4):515-520. [9]杨莉琼,李世蓉,贾彬.基于二元决策图的建筑施工安全风险评估[J].系统工程理论与实践,2013,33(7):1889-1897. [10]翟越,李楠,艾晓芹,等.BIM技术在建筑施工安全管理中的应用研究[J].施工技术,2015,44(12):81-83. [11]王友国,王秀代.基于Gray-Shapley的大型工程项目施工安全风险评价研究[J].建筑技术,2017,48(3):289-292. [12]安磊,王绵斌,谭忠富.基于集对故障树法的输变电工程风险评估模型[J].华东电力,2011,39(1):12-18. [13]姚俊伟,何奇,骆子潆,等.基于AHP的输变电工程安全性后评价体系研究[J].电力学报,2016,134(5):419-423. [14]潘华,高杨杨,薛小龙,等.基于三角模糊数的输变电工程模糊综合评价[J].工程管理学报,2015(4):78-83. [15]高杨杨,潘华,薛小龙,等.基于三角模糊数的云模型在输变电工程项目安全评价中的应用[J].科技管理研究,2016,36(13):53-57.
3 多层次灰色评价模型的构建
3.1 确定评分标准及层次指标权重
3.2 确定指标灰色评价权向量
3.3 确定指标灰色评价权矩阵
3.4 多层次综合评价
4 实例应用
4.1 工程实例背景
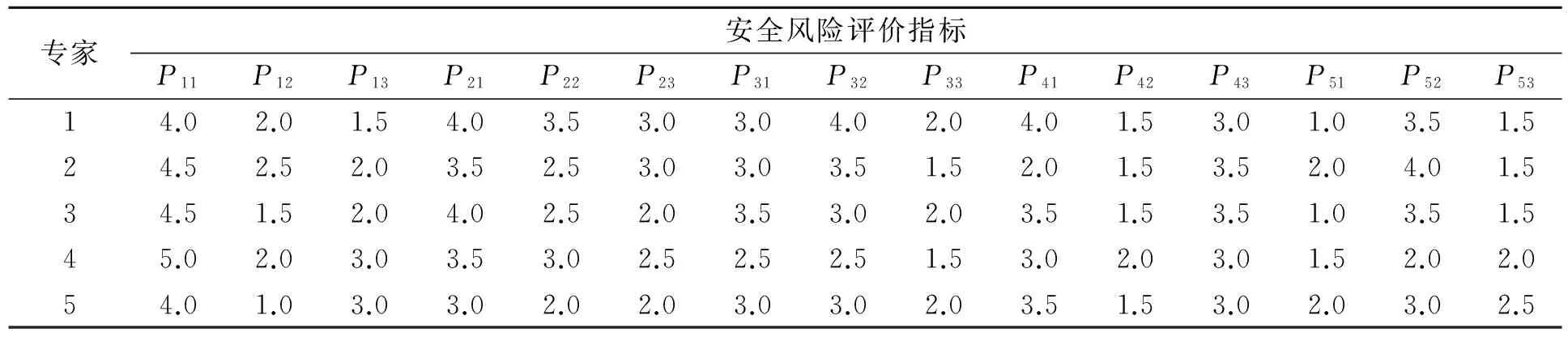
4.2 确定指标权重
4.3 多层次灰色评价
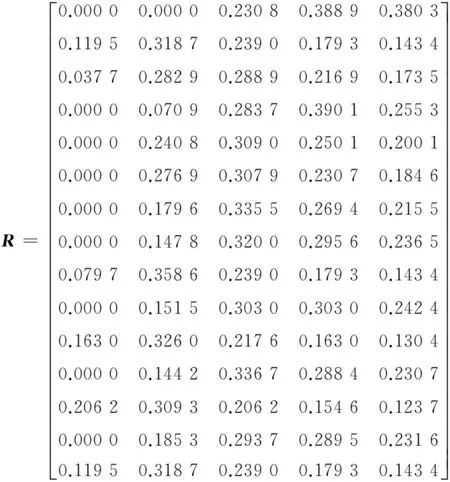

5 结论
