一种表面结构多尺度融合测量系统

王生怀　徐风华　陈育荣　谢铁邦

1.湖北汽车工业学院机械工程学院，十堰，4420022.华中科技大学机械科学与工程学院，武汉，430074

0　引言

在科学与工程领域，由机械加工、电化学处理和表面处理等工艺过程形成的物体表面结构，与机器运行、制造过程、质量控制以及一般的摩擦学都有着密切关系，因此表面结构的测量与评定尤为重要[1-3]。传统的表面形貌测量方法和系统在一定程度上也能满足现代科学与工程表面结构的测量要求[4-8]，这些方法有各自的优势和局限，具体应用取决于被测对象的表面特性和测量要求。但是，传统的表面形貌测量方法由于其本身测量原理及其测量范围、测量精度等的限制，无法满足科学与工程表面结构测量的高精度、大量程和非接触等多尺度要求。

国外学者将光学干涉显微镜和原子力显微镜结合[9]，用于提高光学显微镜的横向和纵向测量分辨率。这种改进在干涉显微镜的视场范围内提高了干涉显微镜的横向和纵向分辨率，但是没有扩大干涉显微镜的测量视场，测量范围受限。英国国家物理实验室工程测量部开发了可溯源的区域表面结构测量仪[10-11]，该仪器采用点接触测量，测量效率非常低，且其触针针尖的大小限制了横向分辨率。国内也进行了显微干涉测量研究，提出了多种改进测量方法，包括表征工程表面的新型两用测量仪[12]、复合型超精密表面形貌测量仪[13-14]、波长轮换与相移扫描相结合的表面形貌测量系统[15]和金刚石砂轮表面形貌测量系统[16]。这些测量系统在一定应用范围内取得了较好的测量效果，但不能满足表面结构的多尺度测量要求。

针对上述问题，本文提出了一种表面结构多尺度融合测量系统。

1　表面结构多尺度融合测量原理

1.1　测量系统总体设计

对于现代科学与工程领域的MEMS器件、NEMS器件、微光学器件等表面结构，现有的单一测量系统已不能满足其表面结构的多尺度测量要求，需要根据被测器件表面结构不同区域的测量要求，采用多个测量系统进行测量。本文提出的多尺度融合测量系统即可实现多种测量方法的多尺度融合测量。测量系统总体设计方案如图1所示，由多尺度融合测量传感器、三维精密位移工作台及图像采集系统、计算机处理系统和工作台测控系统组成。

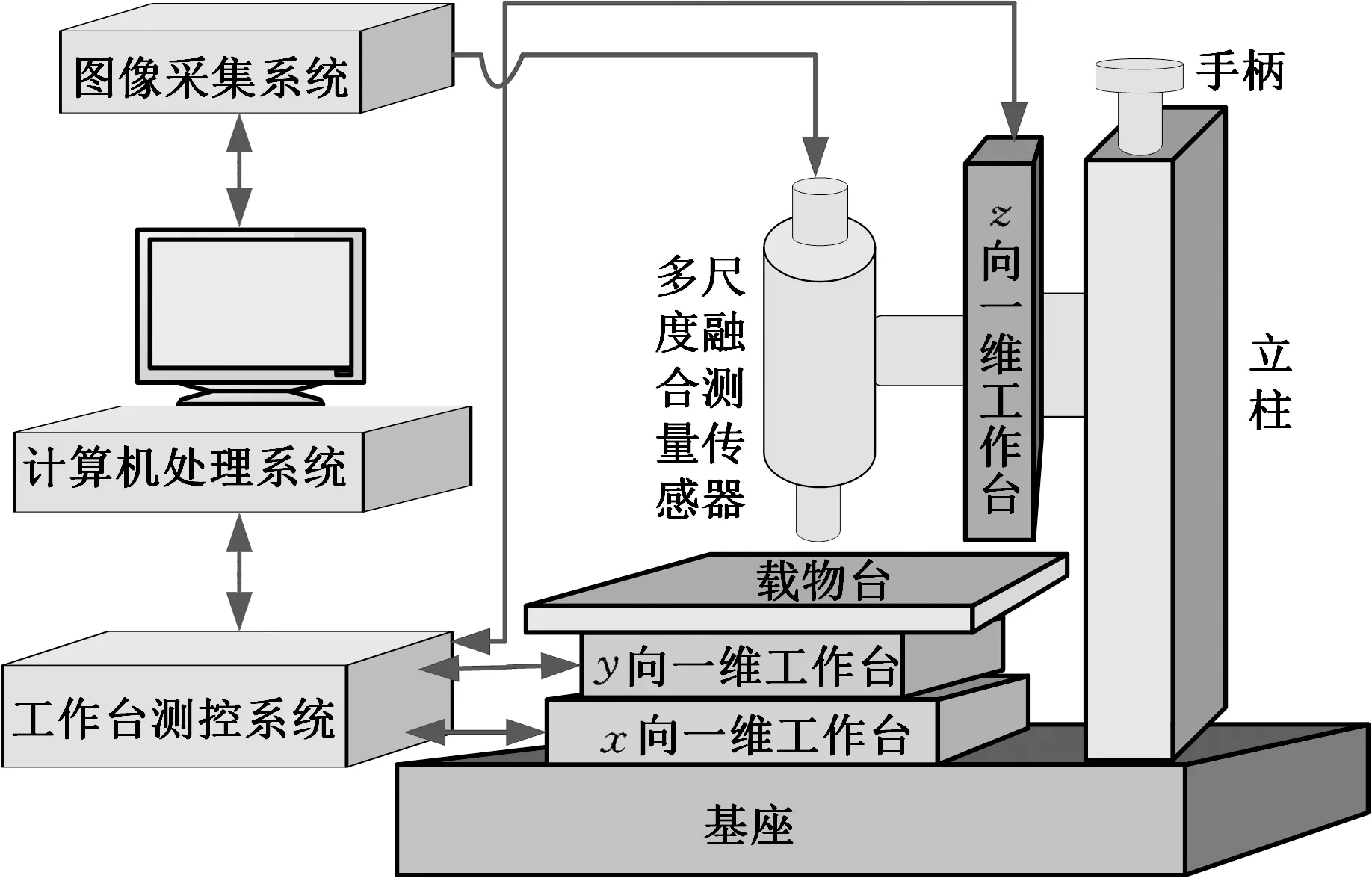
图1　多尺度融合测量系统示意图Fig.1　Diagram of multi-scale integration measurement system

1.2　多尺度融合测量传感器

如图2所示，传感器由光源光路、参考光路、测量光路和采集装置四部分组成。光源光路包括光源S、聚光镜O1和O2、滤光片F、孔径光阑Q1、视场光阑Q2、照明物镜O3。参考光路包括补偿光楔W1、物镜O5、反射镜P1。测量光路包括补偿光楔W2、物镜O4、纳米探针N1、金刚石探针C1和被测表面P1。采集装置主要包括CCD成像装置和图像采集卡。

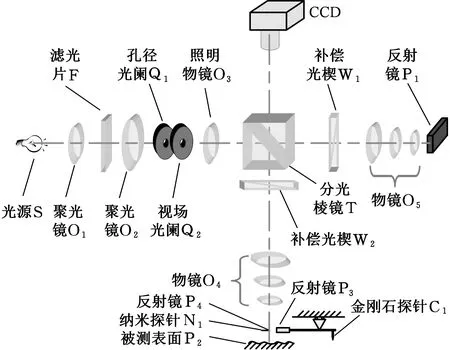
图 2　多尺度融合测量传感器原理图Fig.2　Diagram of multi-scale integration measurement sensor

光源S发出的光线经光源光路后，投射到分光棱镜T上，被分成两部分，一部分反射，一部分透射。从分光棱镜T透射的光经参考光路射向反射镜P1，并被反射重新通过参考光路，通过分光棱镜T改变方向，射向CCD；从分光棱镜T反射的光经测量光路射向被测表面P2，再被反射重新通过测量光路，透射经过分光棱镜T，射向CCD。来自参考光路和测量光路的两束光结合，产生干涉，形成干涉条纹，并被CCD接收，从而构成多尺度融合测量传感器的垂直扫描白光显微干涉测量光路。补偿光楔W1和W2分别用来调整对应光路的光程差。

反射镜P1工作模式分为干涉测量模式和显微图像测量模式。在干涉测量模式下，反射镜P1将来自分光棱镜T的光反射回分光棱镜T，参与干涉。在显微图像测量模式下，通过改变反射镜P1与参考光路的角度，来自分光棱镜T的光不反射回分光棱镜T，传感器相当于一般的显微镜，从而构成显微图像测量光路。

在干涉测量模式下，将纳米探针N1移入物镜O4的焦平面位置，纳米探针针尖背面的反射镜P4朝上，且物镜O4的光轴线通过该反射镜的中心。此时，投射在P4上反射回去的白光和投射在P1上反射回去的白光形成干涉条纹，并在CCD上成像。

以白光作为光源，光谱带宽为Δk，中心谱线波数为k0(k0=2π/λ0，λ0为中心波长)，假设其他参数与波数k无关，以CCD成像面为xy平面，并使成像于CCD平面的干涉条纹方向平行于y方向，对所有谱线在干涉场中的光强进行积分，可以得到光强分布[14]：

(1)

p=sin2α-sin2θk=2π/λ

式中，A为光振幅常量；M为显微物镜放大倍数；d为单透镜成像系统物平面到透镜平面的距离；λ为光源波长；α为参考反射镜绕物镜光轴转角；θ为探针微悬臂偏转角；Δz为探针微悬臂变形量。

可见干涉条纹是被sinc函数调制的余弦函数。利用零光程差条件，可得纳米探针悬臂变形量与条纹移动量的关系：

(2)

在测量过程中，α和M为定值，而θ角随着被测表面结构的变化有微小变动，从而使探针微悬臂变形量与干涉条纹移动量之间产生非线性关系，引起测量误差。

测量过程中，被测表面结构垂直方向上的高度变化引起了纳米探针沿物镜O4的光轴线方向的位移，从而导致CCD上白光干涉条纹在CCD相面上的移动。当条纹的移动未超出相面时，可直接利用条纹的移动量来计算纳米探针的位移量，从而得出被测表面结构的高度信息；当条纹的移动超出相面时，则通过垂直扫描工作台重新将干涉条纹拉回相面，此时结合相面和垂直工作台的位移即可计算纳米探针的位移量，从而得出被测表面结构的高度信息。为了解决式(2)的非线性问题，可直接利用零级条纹的初始位置来定位。

对于表面结构差异较大的结构表面，白光干涉垂直扫描或纳米探针均难以进行测量。此时可在白光干涉测量模式下，将与金刚石探针C1相连的反射镜P3移入物镜O4的焦平面位置，将被测表面移到金刚石探针C1下，采用上述纳米探针类似的计量方法，实现对被测表面结构的金刚石探针扫描测量。

1.3　三维精密位移工作台

三维精密位移工作台结构设计[17]如图1所示，由x、y和z三个方向的一维精密位移工作台构成。

x向、y向和z向的三个一维精密位移工作台的结构设计完全相同，采用模块化设计，位移执行部件和位移计量部件均相同，从而便于重构，其结构如图3所示。

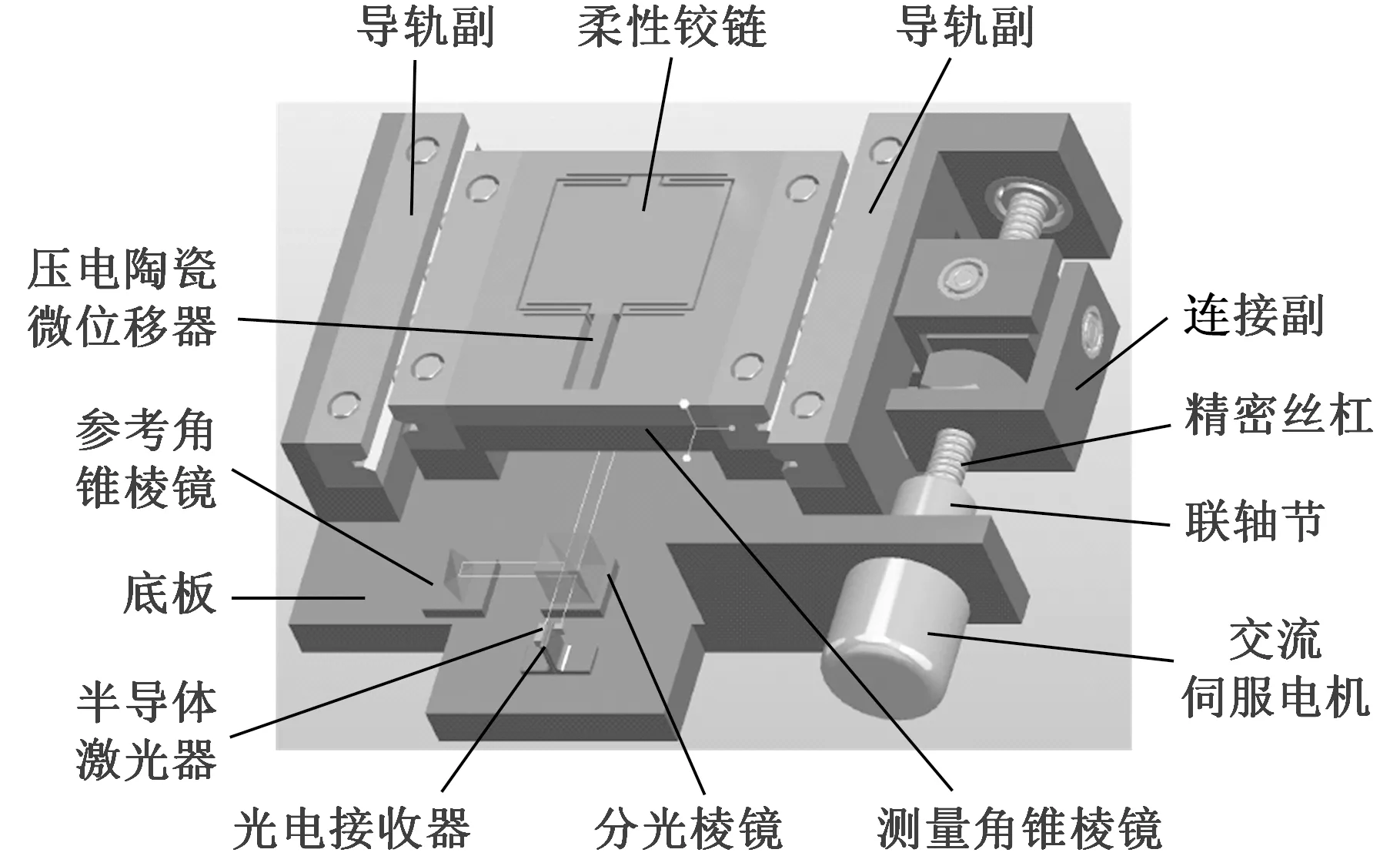
图3　一维精密位移工作台结构简图Fig.3　Diagram of 1D precision displacement worktable

一维精密位移工作台采用粗、精两级驱动。其中，粗驱动行程可达50 mm，分辨率可达0.2 μm，精驱动行程可达20 μm，分辨率可达0.1 nm。工作台位移计量装置采用迈克尔逊干涉原理，在柔性铰链底部安装测量角锥棱镜，在底板上安装参考角锥棱镜。在分光棱镜前侧安装双半导体激光器和光电接收器，形成一个位移检测系统。粗、精两级驱动共用一个检测系统，从而构成一维精密位移工作台的闭环控制系统，结合行程开关，实时修正位移执行部件的位移误差。一维精密工作台测控系统如图4所示。

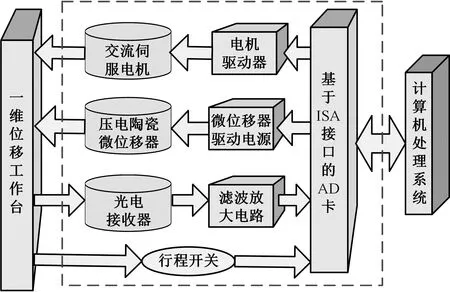
图4　一维精密位移工作台测控系统简图Fig.4　Diagram of measurement and control system for 1D precision displacement worktable

1.4　单场与融合测量

在单场测量工作状态下，测量系统可实现显微图像测量、垂直扫描白光干涉测量和纳米探针测量三种独立测量模式以及融合测量。

对于前两种独立测量模式，当表面结构的被测区域不超过测量物镜的视场时，只需要移动垂直扫描z向一维精密位移工作台，水平方向的x、y二维精密位移工作台则不需要移动。光学显微图像测量通过自动聚焦获取清晰的图像，z向一维工作台对被测区域进行垂直扫描；垂直扫描白光显微干涉测量同样也是z向一维工作台对被测工件进行垂直扫描。在这两种测量模式下，CCD采集的信号分别是光学显微图像和白光显微干涉图像，两种图像的特征值分别为图像清晰度和干涉条纹对比度。由于垂直扫描白光显微干涉测量需要获取扫描过程中的每一幅图像，而光学显微图像测量只需要某一幅清晰的图像，因此，首先通过实验确定垂直扫描白光干涉测量模式下的干涉成像条纹对比度和显微图像测量模式下的显微成像清晰度的对应关系，从而根据测量需要在前后两种测量模式中实时切换，这样得到的二维平面图像和三维图像相对应，实现二维、三维融合测量。其中，横向分辨率取决于光学镜头的放大倍数，本系统采用40倍放大物镜，可获得小于1 μm的横向分辨率，纵向分辨率取决于干涉条纹的分辨率，可达1 nm，测量范围最大可达50 mm×50 mm。

由于光学镜头横向分辨率的限制，前两种测量模式的分辨率只能达到亚微米级。对于第三种测量模式，在白光干涉模式下，将纳米探针移入测量光路，传感器主体内部的白光经过内部的分光镜分光后，一部分经过测量物镜至微悬臂探针针尖顶部的反射镜P4上并被反射，进入传感器主体内部；另一部分通过参考物镜投射到反射镜P1上并被反射回传感器主体内部，与微悬臂探针针尖顶部反射镜反射的白光汇聚，产生白光干涉条纹。干涉条纹经传感器主体内部的放大镜放大后，在CCD探测器成像平面上成像；微悬臂探针针尖沿着测量物镜光轴轴线方向的移动，改变了测量光路的光程，导致白光干涉条纹产生移动，计算CCD成像平面上干涉条纹移动量，即可获得对应的纳米探针针尖沿测量方向的移动量。启动压电陶瓷微位移器，驱动xy向精密位移工作台的柔性铰链在水平方向进行扫描，即可实现三维纳米测量。

假设白光光源中心波长为λ0，白光干涉条纹在CCD上成像后所占像元数为N，则CCD接收干涉条纹的分辨率为

(3)

将干涉条纹的宽度调到3 mm，所占像元个数约为300，零级条纹扫过这些像元时，两像元之间的分辨率为0.275 μm/300，因此纳米探针测量的分辨率约为1 nm。若采用亚像素技术，可得到小于0.1 nm的分辨率。测量前先转动反射镜，使反射镜反射的参考光未被反射回参考物镜，测量物镜光路构成了显微放大光路，能对测量区域进行显微放大，从而直接观察被测区域。一般情况下，纳米探针悬臂梁的宽度为几十微米，在采用合适倍数物镜条件下，CCD探测器的视场可达几百微米，可将多个探针并排布置，使之分别在CCD探测器的视场中形成干涉条纹，从而实现多探针同时测量，提高测量效率。纳米探针的横向测量范围取决于三维精密位移工作台的移动范围。考虑到纳米测量的有效性，一般取20 mm×20 mm测量范围即可满足使用要求。

1.5　拼接、融合测量与定位

测量系统的横向分辨率受限于物镜数值孔径，数值孔径的增大提高了测量横向分辨率，但是使测量视场减小，影响了系统的测量范围。为获取大面积高倍率二维、三维表面结构光学显微图像，基于测量系统自带的三维精密位移工作台，在物镜横向分辨率达到极限分辨率0.2 μm的情况下，采用精密定位子孔径拼接方法，即可满足大面积高倍率二维、三维表面结构光学显微图像的无特征、无痕和无缝拼接测量要求。在拼接测量过程中，结合本文的单孔径互融测量，即可得到满足要求的图像。

在拼接测量过程中，需要通过水平精密二维位移工作台将物体逐场移动到测量物镜视场下，以供CCD成像。这里假设CCD成像面和水平精密二维位移工作台所在空间平面平行，只考虑CCD成像面投影到水平工作台上的情况。如图5所示，以CCD成像面OA和OB建立成像面坐标系。水平工作台x向和y向导轨所在方向分别用OP1和OP2表示，建立工作台坐标系。由于安装误差，CCD坐标系分别与水平工作台的OP1和OP2之间存在的夹角为α和β。CCD成像面采用粗实线框1表示，即被测样件的成像区域。点划线框2表示X向工作台驱动样件沿导轨方向OP1从O点移动到P1点位置，虚线框3表示Y向工作台驱动样件沿着导轨方向OP2从O点移动到P1点位置。

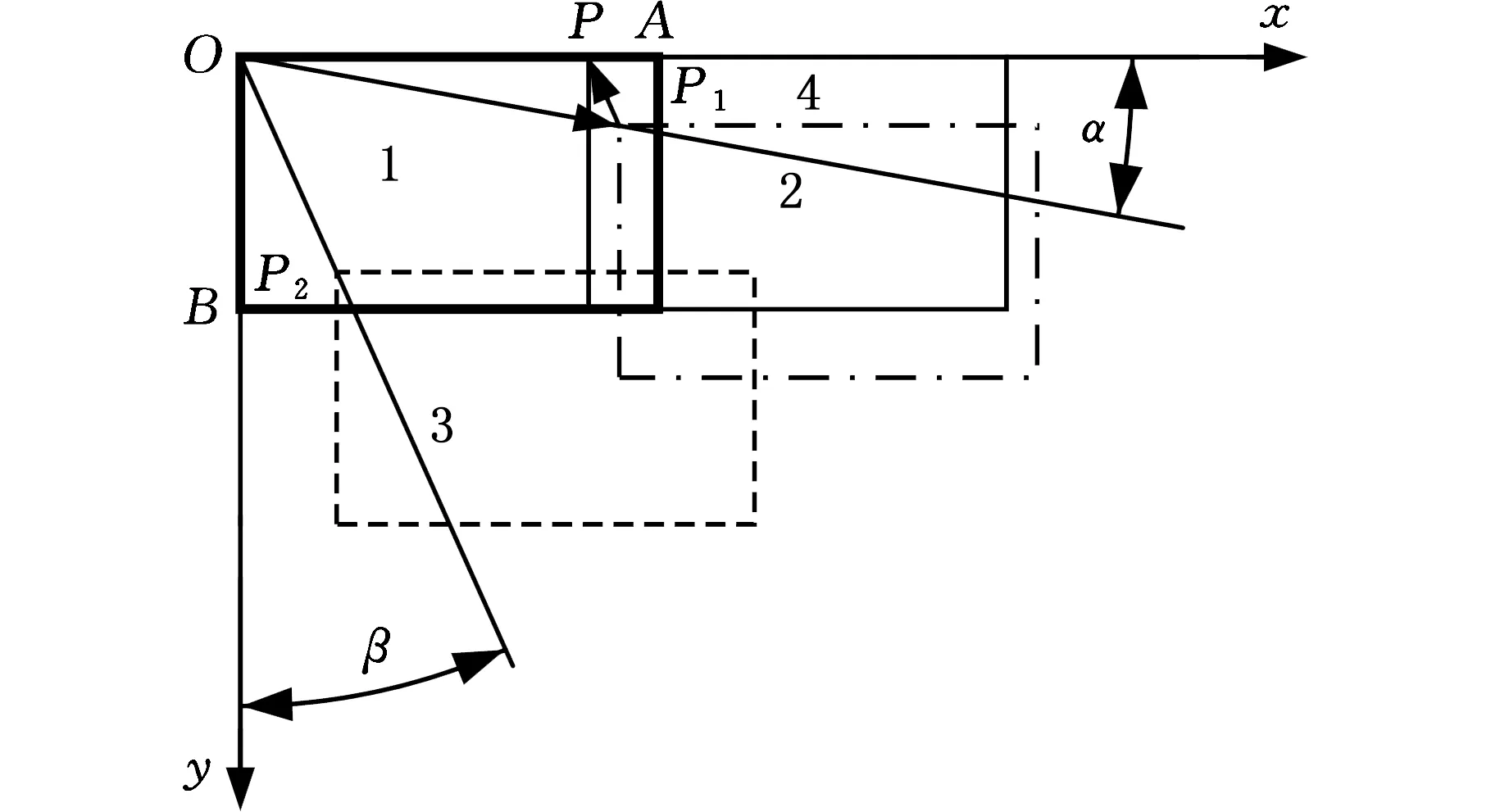
图5　工作台移动路径Fig.5　Moving path of the worktable

为提高拼接效率，被测区域需逐场水平进入CCD成像。如图5所示，假设要将被测区域从框1所示区域横向平行移动到框4所示区域，且两区域部分重叠，重叠宽度为PA。由于存在α和β，则需要通过两步平移达到。以P点作OP2的平行线交OP1于P1点，首先x向工作台驱动样件沿OP1移动到P1点，然后y向工作台驱动样件沿OP2移动到P点，从而补偿了由于水平二维精密位移工作台安装误差而产生的拼接错位。在被测区域纵向平行移动时，产生的拼接错位也采用同样的办法解决。作为一般化，假设被测区域在CCD成像面坐标系下的某一位置为(dx,dy)，则水平二维精密位移工作台需要移动的位移(Wx,Wy)为

(4)

其中，测量系统的α和β为定值，并可采用测量系统本身自带的计量装置进行测定[18]。

由于表面结构的多尺度性，有时只需要对某些含有较多结构特征的区域进行测量，并不需要对整个被测区域进行三维垂直扫描的子孔径拼接测量，因此，在进行三维测量前，先获取整个被测区域的二维显微拼接图像，并对图像进行基于形态学的自动分割和分类识别，再根据需要进行定位三维垂直扫描测量。对于那些横向测量分辨率要求超过光学镜头横向分辨率的区域，则切换到纳米探针测量模式下实行三维纳米测量。

1.6　金刚石探针扫描测量

采用金刚石探针扫描测量主要有两个目的：①充分利用传感器的系统资源，使之在传感器现有资源条件下，稍微增加一些零部件，即可增加传感器的测量功能；②增加金刚石探针扫描测量功能，可克服显微图像测量、白光干涉垂直扫描测量和纳米探针测量这几种方法的不足，满足表面结构多尺度特性的测量要求。

在白光干涉测量模式下，将与金刚石探针C1相连的反射镜P3移入物镜O4的焦平面位置，将被测表面移到金刚石探针C1下，白光束通过分光镜，一束到达参考镜，另一束通过分光棱镜到达反射镜P3，两束光返回到分光面产生干涉条纹。x、y工作台移动，被测表面的变化由金刚石触针感测，通过杠杆带动反射镜P3移动，引起干涉条纹移动，CCD采集条纹移动量，经过计算机系统进行处理，即可得出金刚石探针垂直方向上的位移，x、y方向位移由x、y工作台测量系统计量。

根据上述纳米探针的测量原理，当干涉条纹的横向分辨率达到纳米级水平时，CCD成像面上只能检测到白光半波长范围内的位移。由于金刚石探针测量范围为毫米级，造成较大纵向位移时白光干涉零级条纹移出CCD视场，因此必须采用相应的测量策略。此时，若金刚石探针的垂直位移使得白光干涉条纹移出CCD视场，需要启动垂直扫描工作台在垂直方向进行扫描，使干涉条纹重新回到CCD视场范围内，并将白光干涉零级条纹作为零位基准，工作台垂直方向位移与干涉条纹在CCD视场范围内移动对应的位移量之和，则是此处被测点在垂直方向的位移。结合x、y工作台在水平方向上的扫描，即可获取被测表面结构的毫米级范围的测量结果。由上文分析可知，白光干涉条纹移动量分辨率和工作台扫描位移计量分辨率均可达到纳米级，因此金刚石探针测量的纵向分辨率可达1 nm。金刚石探针的横向测量范围取决于三维精密位移工作台的移动范围，可达50 mm×50 mm测量范围。此外，为了易于判断垂直工作台需要扫描的方向，可附加电感位移传感器辅助判断方向。

目前，纳米探针测量和金刚石探针测量需要交替更换，在一定程度上影响测量效率，但是若进一步设计成光学显微镜旋转镜头的工作模式，则测量效率不受影响。由于两个测头整体更换，且测量精度主要取决于三维工作台精度和对干涉条纹的分析，因此不影响测量精度和重复性，不需要每次和标准样板比对。

2　实验装置和测量数据

2.1　实验装置

根据上述原理搭建的实验装置如图6、图7所示。

图6　多尺度融合测量系统实物图Fig.6　Prototype of multi-scale integration measurement system

(a)纳米探针测头　(b)金刚石探针测头图7　纳米探针测头和金刚石探针测头Fig.7　Nano-probe measuring head and diamond-probe measuring head

2.2　二维显微图像测量

在二维显微图像测量模式下，需对图像与实物之间的尺度关系进行标定。以一等标准玻璃线纹尺为标定量具，线纹尺刻线总长为1 mm，刻线间距为10 μm，检定精度为±(0.1+0.5L) μm，L为检定长度(m)。线纹尺的单场显微图像如图8所示。为验证显微图像测量的标定结果，对单场刻线的不同刻度值分别进行10次显微图像测量，可得300 μm时的示值误差为-0.251 μm，标准偏差为0.401 3 μm。

图8　标准尺的单场显微图像Fig.8　Single aperture microscopy image of standard ruler

图9为1×4孔径拼接显微图像，通过拼接显微图像，可对基本尺寸大于单孔径视场的被测物进行高分辨率的图像拼接测量。

图9　标准尺的1×4孔径拼接图Fig.9　Stitching microscopy image of 1×4 apertures of standard ruler

2.3　三维白光干涉测量

为验证三维白光干涉测量结果的有效性，采用具有微米级深度的单刻线样板进行验证。刻线样板表面结构如图10所示，包括水平方向的主刻线和与之垂直的四条辅助刻线。

图10　单刻线样板表面结构Fig.10　Surface texture of single line template

以两种不同刻线深度的单刻线样板进行验证，由中国计量科学研究院检定的样板刻线深度结果分别为1.26 μm和3.33 μm，本系统测得的单场三维表面结构如图11、图12所示，计算得到两样板刻线深度的平均值为1.263 μm 和3.328 μm，对应的示值误差为0.003 μm和 -0.002 μm，示值相对变化量为1.27%和0.63%。

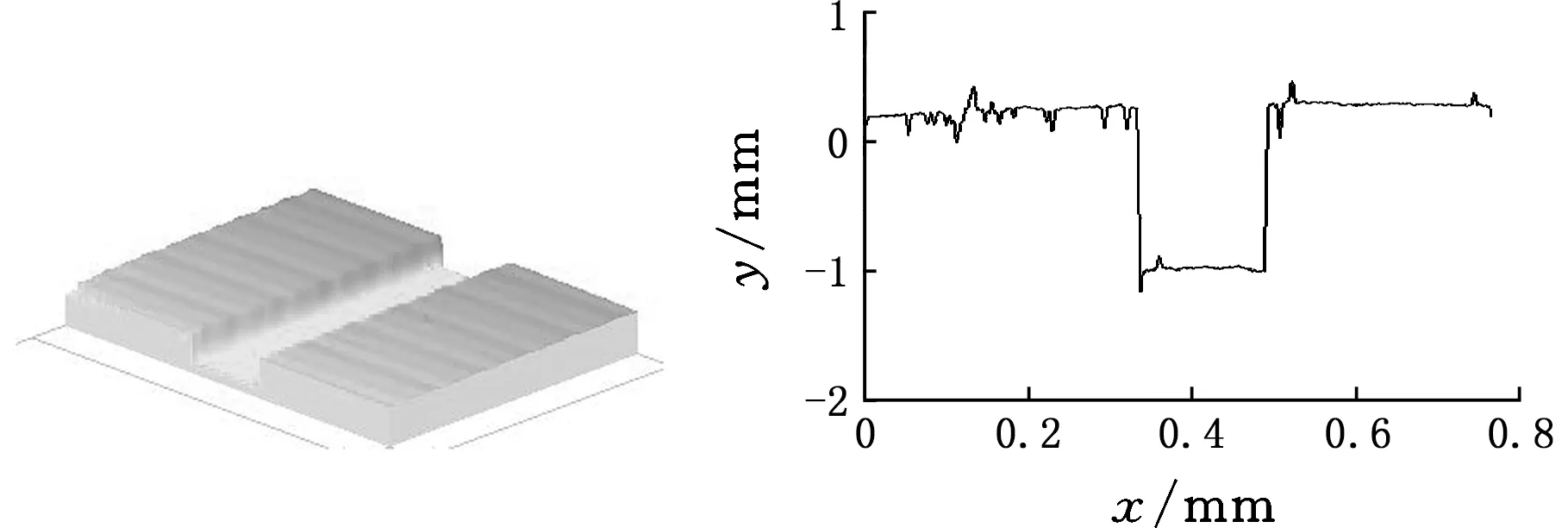
图11　深度为1.26 μm的单刻线样板的测量Fig.11　Measurement of single line template with depth of 1.26 μm

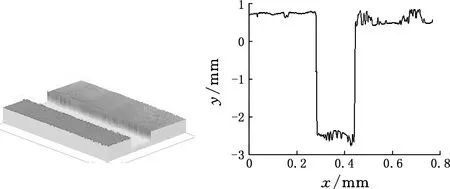
图12　深度为3.33 μm的单刻线样板的测量Fig.12　Measurement of single line template with depth of 3.33 μm

图13为单刻线样板部分刻线的3×3孔径拼接测量，在保持单场较高分辨率的情况下，有效扩大了测量视场。

图13　单刻线样板的3×3孔径拼接测量Fig.13　Measurement of 3×3 aperture for single line template

2.4　白光干涉纳米探针测量

为验证白光干涉纳米探针测量结果的有效性，采用扫描探针校准光栅进行验证。校准光栅型号为TGZ2，经德国PTB认证，该光栅高度为(106.8±1.0)nm，周期为(3.00±0.01)μm。选取光栅上三个不同的有效位置进行测量，获得三条对应的轮廓曲线，分别获得三个位置的高度平均值，最后取平均得到该校准光栅高度的平均值为103.1 nm，相对示值误差为-3.5%。测量数据如表1所示，其中一条测量轮廓曲线如图14所示。

表1　测量结果与示值误差Tab.1　Measurement results and indication error

图14　TGZ2样板测量轮廓曲线Fig.14　Measurement profile curve of template TGZ2

2.5　白光干涉金刚石探针测量

为验证白光干涉金刚石探针测量结果的有效性，采用金属刻线表面粗糙度样板进行验证。样板型号为A05149，刻线为4根/mm，由中国计量科学研究院检定Ra=4.08 μm。

取采样长度为1.5 mm，采样间隔为1 μm，经软件算法和数据处理后得Ra=4.05 μm，测得值的相对误差为0.74%。图15所示为A05149样板测量后得到的一条二维粗糙度曲线。

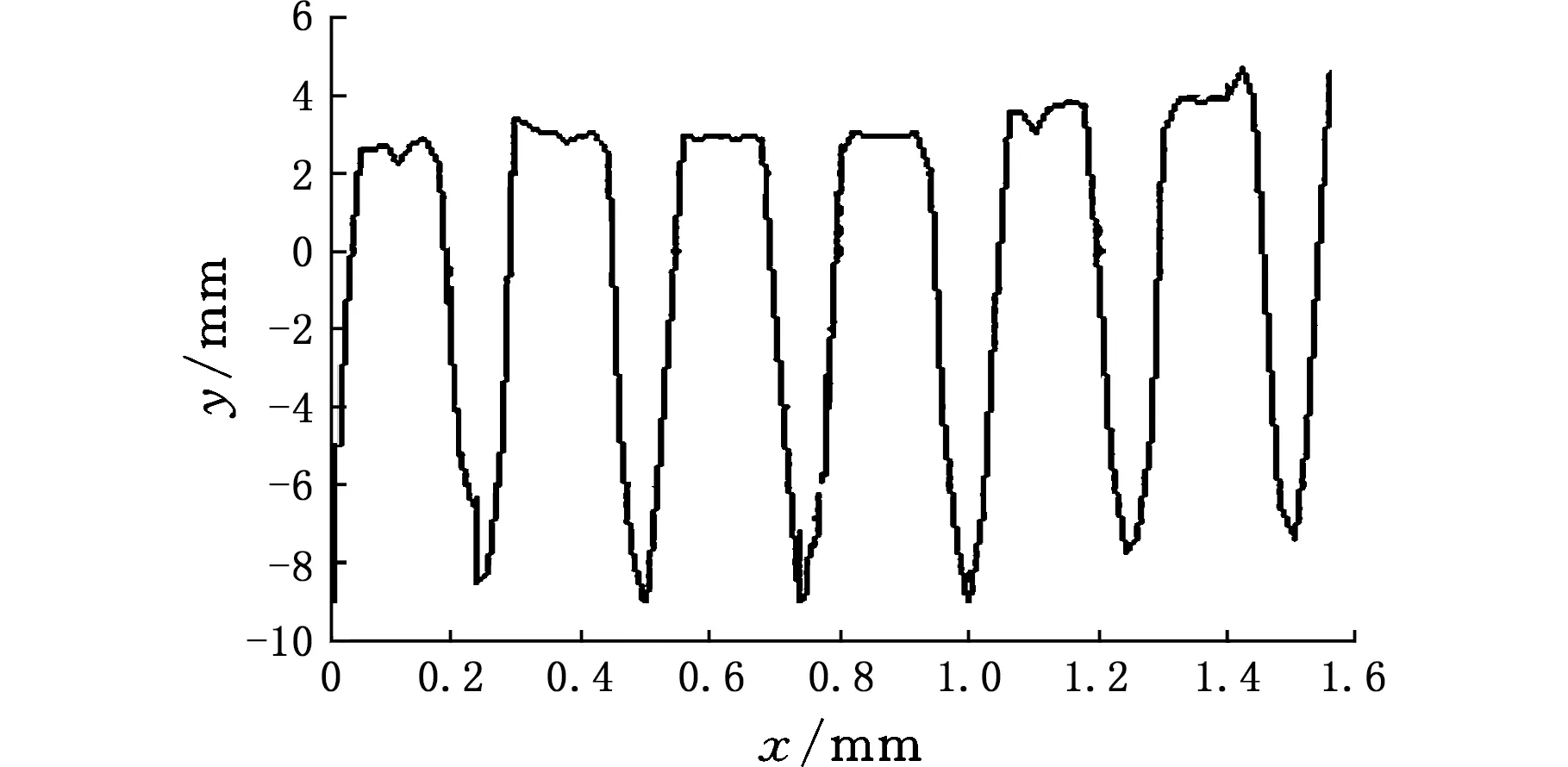
图15　A05149样板二维粗糙度曲线Fig.15　2D roughness curve of template A0519

3　结语

本文提出的表面结构多尺度融合测量系统充分利用一套光学显微干涉系统主体结构，融合多种测量方法，满足现代科学与工程表面结构的多尺度融合测量需要。此外，可依托该测量系统获取三维表面结构测量时对应的二维显微图像，实现区域表面结构的二维分割，进一步实现对三维数据的分割，有利于采用流域分割法对三维点阵测量数据进行分割和3D-Motif参数计算与评定，从而获得更全面的表面结构特征及其评定结果。

参考文献：

[1]JIANG X, SCOTT P J, WHITEHOUSE D J, et al. Paradigm Shifts in Surface Metrology. Part I. Historical Philosophy[J]. Proceedings Mathematical Physical & Engineering Sciences, 2007, 463(2085):2049-2070.

[2]JIANG X, SCOTT P J, WHITEHOUSE D J, et al. Paradigm Shifts in Surface Metrology. Part II. the Current Shift[J]. Proceedings Mathematical Physical & Engineering Sciences, 2007, 463(2085):2071-2099.

[3]HU Z M, DEAN T A. A Study of Surface Topography, Friction and Lubricants in Metalforming[J]. International Journal of Machine Tools & Manufacture, 2000, 40(11):1637-1649.

[4]CLARK S R, GREIVENKAMP J E. Ball Tip-stylus Tilt Correction for a Stylus Profilometer[J]. Precision Engineering, 2002, 26(4):405-411.

[5]CHU C L, LIN C H, FAN K C. Two-dimensional Optical Accelerometer Based on Commercial DVD Pick-up Head[J]. Measurement Science & Technology, 2007, 18(1):265-274.

[6]FAN K C, CHEN L C, LIN C D, et al. Development of Dynamic 3-D Surface Profilometry Using Stroboscopic Interferometric Measurement and Vertical Scanning Techniques[J]// Journal of Physics Conference Series, 2007，13(1):51-54.

[7]SCHMIT J, OLSZAK A. High-precision Shape Measurement by White-light Interferometry with Real-time Scanner Error Correction[J]. Applied Optics, 2002, 41(28):5943-5950.

[8]LI J, TOTH M, TILELI V, et al. Evolution of the Nanostructure of Deposits Grown by Electron Beam Induced Deposition[J]. Applied Physics Letters, 2008, 93(2):619.

[9]JOBIN M, FOSCHIA R. Improving the Resolution of Interference Microscopes[J]. Measurement, 2008, 41(8):896-903.

[10]LEACH R. Some Issues of Traceability in the Field of Surface Topography Measurement[J]. Wear, 2004, 257(12):1246-1249.

[11]LEACH R, CHETWYND D, BLUNT L, et al. Recent Advances in Traceable Nanoscale Dimension and Force Metrology in the UK[J]. Measurement Science & Technology, 2006, 17(3):467-476.

[12]YUN J P, CHANG S P, XIE T B, et al. A Novel Contact and Non-contact Hybrid Profilometer[J]. Precision Engineering, 2009, 33(2):202-208.

[13]WANG S Z，XIE T B，CHANG S P. A White Light Interference-based Atomic Force Probe Scanning Microscopy [J]. Measurement Science & Technology, 2011, 22 (4): 045502.

[14]王淑珍，谢铁邦，常素萍.复合型超精密表面形貌测量仪[J]. 光学精密工程,2011, 19(4):828-835.

WANG Shuzhen，XIE Tiebang，CHANG Suping. Combined Profilometer for Ultra-precision Surface Topography[J]. Optics and Precision Engineering, 2011,19(4):828-835.

[15]杨练根，何浪，王选择，等. 波长轮换与相移扫描相结合的表面形貌测量系统[J].光学精密工程,2015,23(9):2466-2472.

YANG Liangen, HE Lang, WANG Xuanze, et al. Surface Topography Measuring System Based on Wavelength Switching and Phase Shift Scanning[J].Optics and Precision Engineering,2015,23(9):2466-2472.

[16]崔长彩，余卿，张遨，等.金刚石砂轮表面形貌测量系统[J].光学精密工程,2014,22(12):3167-3174.

CUI Changcai, YU Qing, ZHANG Ao, et al. Measurement System of Surface Topography for Diamond Grinding Wheel[J]. Optics and Precision Engineering, 2014,22(12):3167-3174.

[17]王生怀,陈育荣,王淑珍,等.三维精密位移系统的设计[J].光学精密工程,2010,18(1):175-182.

WANG Shenghuai, CHEN Yurong, WANG Shuzhen,et al. Design of 3D Precision Displacement System[J]. Optics and Precision Engineering, 2010, 18(1):175-182.

[18]王生怀，徐风华，陈育荣，等.基于三维精密位移工作台的显微图像拼接测量系统[J].机械设计与制造，2012(2):70-72.

WANG Shenghuai, XU Fenghua, CHEN Yurong, et al. A Microscopy Image Stitching Measurement System Based on 3D Displacement Worktable[J]. Machinery Design &Manufacture，2012(2):70-72.

(编辑王旻玥)