某水下机器人阻力特性的数值模拟*

白航, 王伟竹, 姚清河

(中山大学应用力学与工程系，广东 广州 510275)

海洋资源的开发和研究不断发展，但水下环境险恶复杂。因人的潜水深度十分有限，机器人已经成为水下开发和研究的重要工具。机器人在水下行进时所受到的阻力对其快速性和运动预报具有重要影响，因此其阻力性能是决定水下机器人综合性能的重要因素之一[1]。同时，水下机器人能源消耗的快慢取决于航行速度的大小和航行时受到的阻力。航速一定的情况下，阻力大小也就成为影响能耗的决定因素[2]。所以，阻力性能研究一直是水下机器人研究的热点[1,3,4]。

当前，模型实验是研究水下机器人阻力性能的主要方法[5-8]。但模型实验存在耗时长、耗资大等问题，不利于水下机器人特别是低成本水下机器人的开发和研究。而，模型试验的结果也容易受到非人为因素的干扰，例如：船池尺度， 温度等。水下机器人结构复杂、外形各异、所附物体种类繁多，当前尚无系统的设计资料可应用于近似计算，若采用水面船舶、潜艇、鱼雷等的经验公式，则不可避免地给阻力的估算带来很大的误差。近年来，运用计算流体动力学(CFD)技术，对水下机器人进行设计和开发等蓬勃发展起来。Zhang等[9]使用CFD方法研究了蝶型水下机器人的阻力性能和不同雷诺数下的流场特性，并与实验数据进行比较，验证了CFD方法的有效性。杨放琼等[10]基于人工势场算法，成功实现了海底不确定环境下集矿机械的实时避障。Georgiades C等[11]开发了一种预测振荡刚性桨叶产生力的模型，并对水下六足机器人 AQUA 进行了模拟计算。 桑恩方[12]对水下机器人在堤坝安全隐患检测方面的应用进行了研究。孙丽[13]使用 Fluent 软件对水下自主机器人运行中的阻力及流动情况进行了研究。宋方希[14]采用计算流体动力学方法，对带机翼的水下自主机器人的阻力特性、水下续航能力稳定性及机动性进行了研究，讨论了带机翼机器人的优缺点并提出了优化建议。Yang等[15]针对水下机器人的实景仿真系统进行了研究与优化。马尧等[16]对鱼型水下机器人在不同航速下的压强和湍动能变化趋势进行了初步研究。Liu等[17]基于虚拟模型的运动特征和CFD模型研究了水下自主机器人的动态位置控制算法。郭丙华等[18]提出了一种机器人移动快速定位的方法，大大降低了定位算法计算的复杂度。王黎阳[19]对水下机器人在深孔有压隧洞环境检测中的应用进行了研究，验证了水下机器人在该环境下的可靠性。Park等[20]运用CFD技术对徘徊型自主水下航行器的运动特性进行了研究。刘源等[21]提出了一种关于浅水环境下水下步行机器人的设计方案，并采用 Fluent 软件对设计方案进行了仿真优化。此外，张爽等[22]利用Simulink进行仿真研究，进一步改善了仿人机器人的步态平衡控制。数值模拟方法可以有效地解决模型实验时间周期长、费用高的问题，可以形象再现流动场景，具有很好的可重复性[1, 5, 7, 23]。在计算流体动力学领域的众多计算软件中，Fluent 是目前国内外使用最多、开发最成熟的软件之一[24]。本文使用 Fluent 计算软件，基于工程实例，运用 CFD 方法对深孔有压隧洞流体环境下某型号水下机器人的阻力特性展开了研究，分析了不同支撑结构的水下机器人在不同工况下的阻力特性，以及机器人周围流场的流速和压力分布。

1　控制方程及数值方法

本文采用雷诺时均法对不可压缩流动控制方程进行时间平均，得到时均N-S连续方程，即雷诺时均N-S方程(RANS)：

(1)

(2)

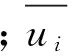
在求解N-S方程时引入湍流模型来封闭方程组[25]，不同的粘性问题应选择不同的湍流模型。根据《微小型水下机器人阻力性能的数值模拟》[3]，两方SSTκ-ω模型在处理此类问题时具有较高的精度。所以，本文选用两方SSTκ-ω模型：

(3)

(4)

式中：Gk是由层流速度梯度而产生的湍流动能；Gω为由ω方程产生的动能；Γk和Γω为k和ω的扩散率；Yk和Yω为由于扩散而产生的湍流；Sk和Sω是自定义的，在设置边界条件时选取SSTκ-ω模型。

2　模型的建立

2.1　物理模型的建立及简化

本文以某型号水下机器人为例，其实际尺寸如表1所示。为了减少下游涡流发展、增加稳定性，双侧履带部件做闭合处理。模型A的前方支撑结构为板件；模型B的前方支撑结构为杆件。A、B两种不同支撑结构机器人的物理模型，如图1所示。

表1　机器人原型尺寸Table 1　Basic dimensions of the robot　　　　mm

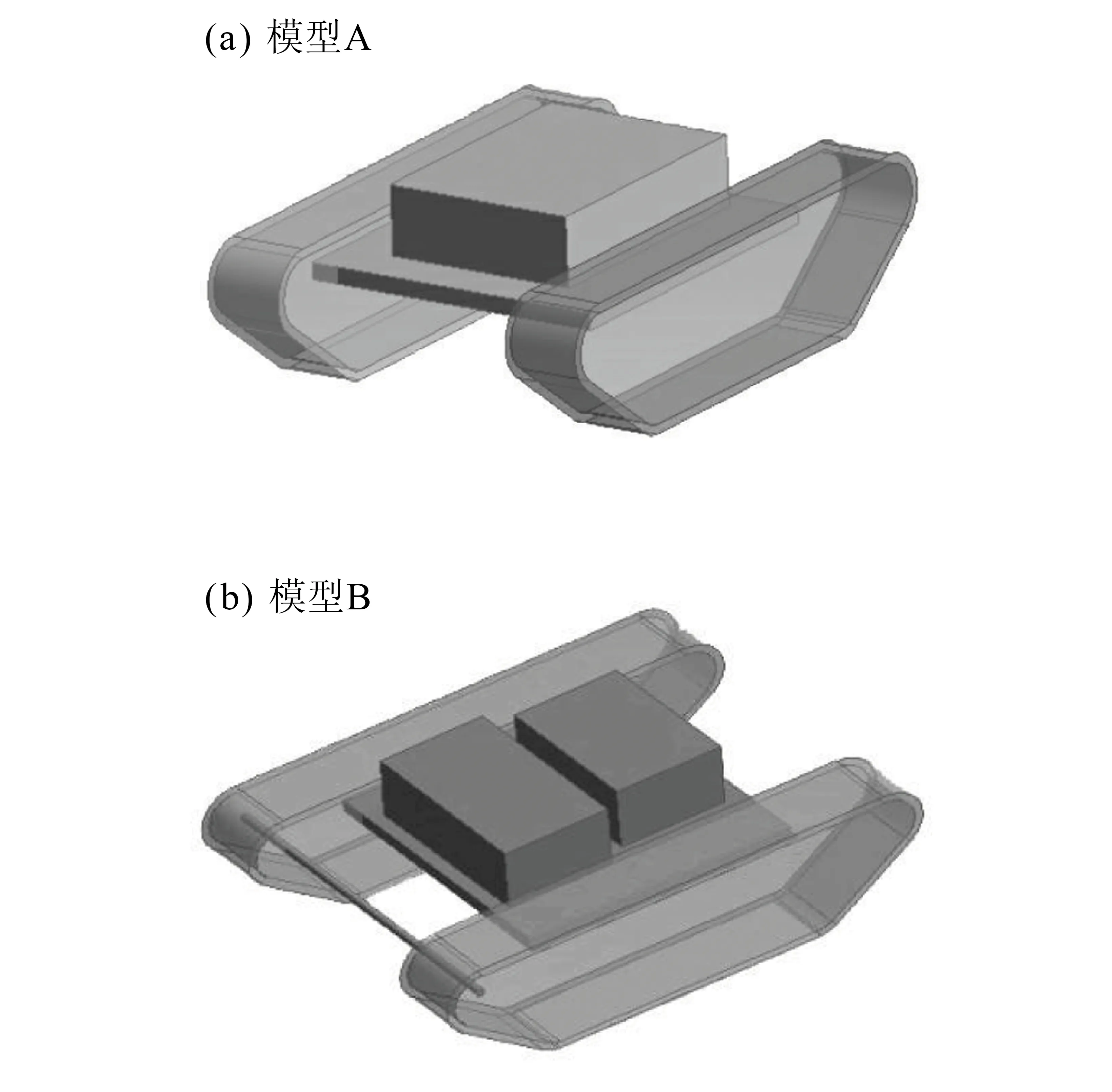
图1　机器人模型图Fig.1　Model diagrams of robot

2.2　网格划分

如图2所示，运用workbench中的meshing软件对模型A和B进行网格划分。运用refinement功能对机器人表面进行网格优化，经过网格独立性检测以后，模型A的总网格数为3 920 054，模型B的总网格数4 008 116。对模拟计算域的尺寸进行设计使其满足计算的最小要求，并进行网格划分，如图3所示。

图2　网格划分Fig.2　Mesh graph

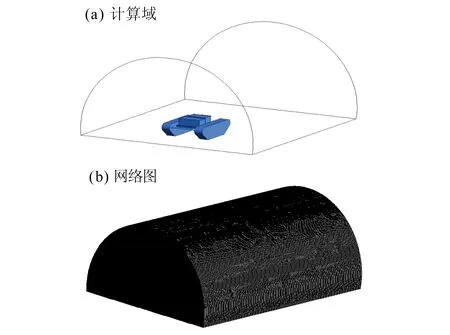
图3 计算域及网格图Fig.3　Computational domain

2.3　计算设定

该隧洞为某工程引水涵洞，为一深孔有压隧洞，中心线高程为-35.5 m，引水流量97.3 m3/s，隧洞直径7.3 m (底部含2.1 m平面)。计算设置为无自由液面管道流动(无兴波阻力)，在隧洞出口处认为流动在该处已充分发展。机器人表面设置为无滑移壁面条件。

在隧洞正常服役条件下，按照该水下机器人的实际功能对两种模型进行了工况划分和分析计算。机器人顺流行驶时速度为正，机器人逆流行驶时速度为负。各工况除行驶速度的大小与方向外，其他参数均不变，具体划分如下：

1)机器人行驶工况 1：机器人在隧洞内以 -20 m/min的速度行驶；

2)机器人行驶工况 2：机器人在隧洞内以 -10 m/min的速度行驶；

3)机器人行驶工况 3：机器人在隧洞内静止；

4)机器人行驶工况 4：机器人在隧洞内以 10 m/min的速度行驶；

5)机器人行驶工况 5：机器人在隧洞内以 20 m/min的速度行驶；

6)机器人行驶工况 6：机器人在隧洞内以 40 m/min的速度行驶。

3　模拟结果与讨论

3.1　有效性验证

为了验证计算方法、参数设置的准确性和模拟结果的有效性，我们对已知试验数据的Suboff标准模型用同样的方法进行计算，并将模拟结果和ITTC(international towing tank conference，国际拖曳水池会议)公布的试验数据进行对比[26]。Suboff计算模型如图4所示。

图4　Suboff模型Fig.4　The standard Suboff model

如表2所示，总体误差在4.5%以内，具有较好一致性，模拟计算结果可靠。这说明本文中所得到的数值模拟结果是有效的。

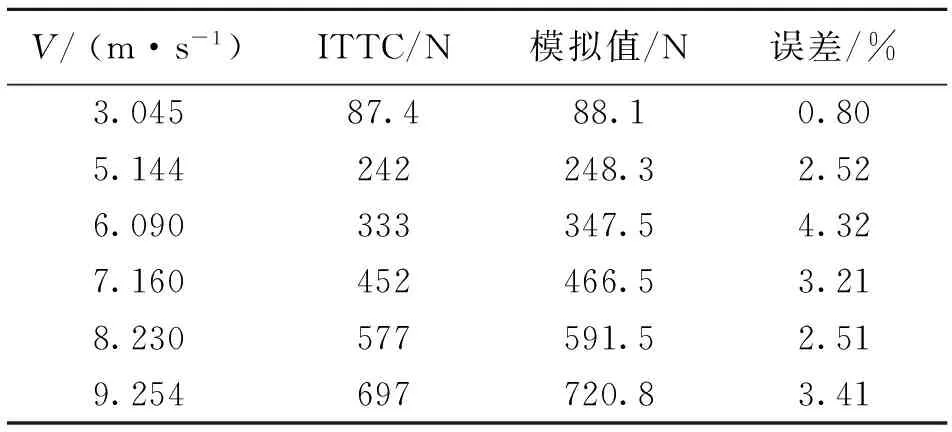
表2　模拟计算结果Table 2　Numerical calculation results

3.2　阻力特性分析

由表3-4可知，在不同工况下模型A受到的阻力大于模型B受到的阻力。模型A承受的压差阻力和总阻力比模型B大约28% ～ 34%，摩擦阻力则为0.88% ～ 2.59%。同时，两种模型所承受到的来流总阻力中，压差阻力都起主要作用，约占总阻力的97% ～ 98%；粘性摩擦阻力所占比重较小，约为2% ～ 3%。

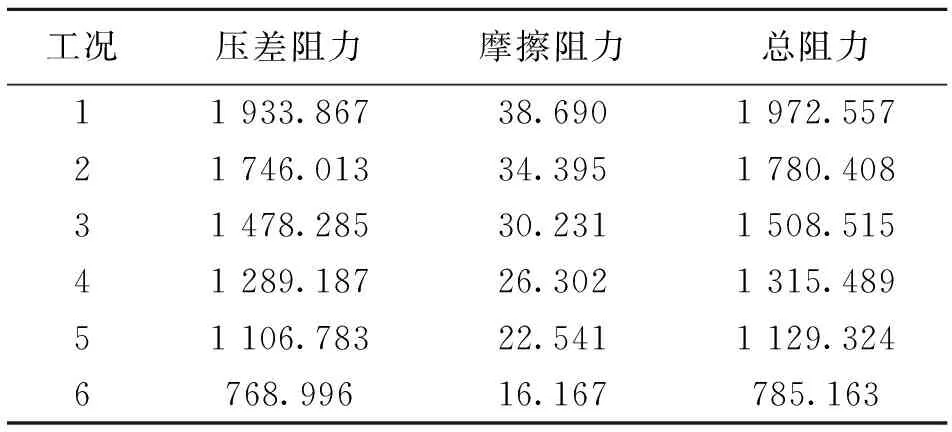
表3　不同工况下模型A的阻力变化情况Table 3　Stress analysis of the model A under different conditions 　N

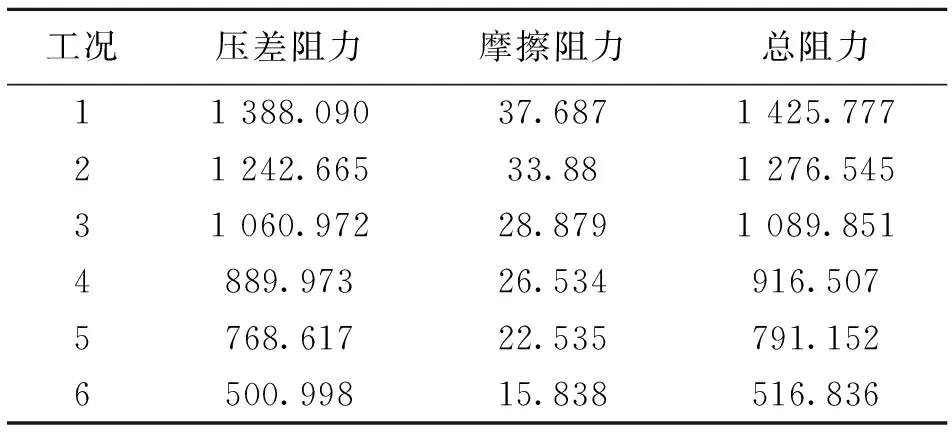
表4　不同工况下模型B的阻力变化情况Table 4　Stress analysis of the model B under different conditions 　N

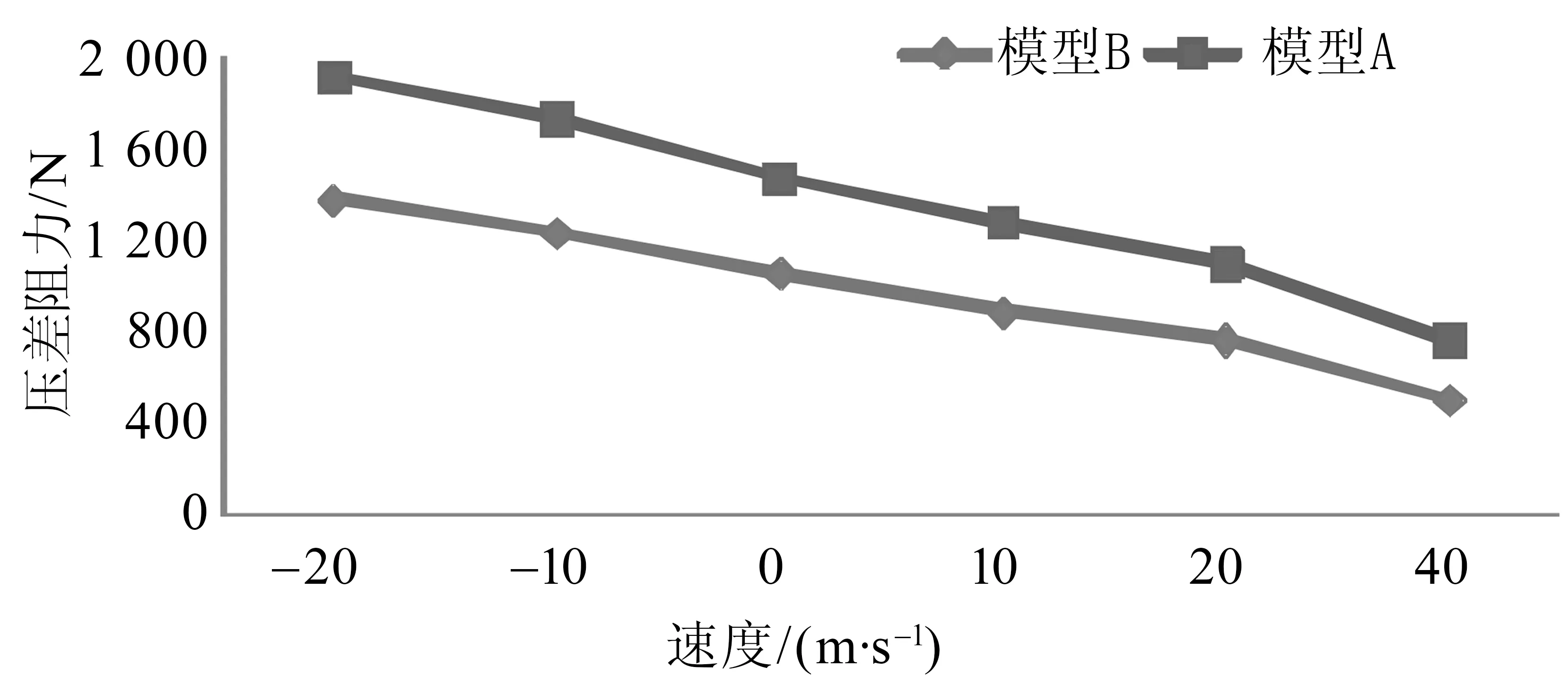
图5　不同工况下A、B模型的压差阻力变化曲线Fig.5　The pressure resistance changing curve of model A and B

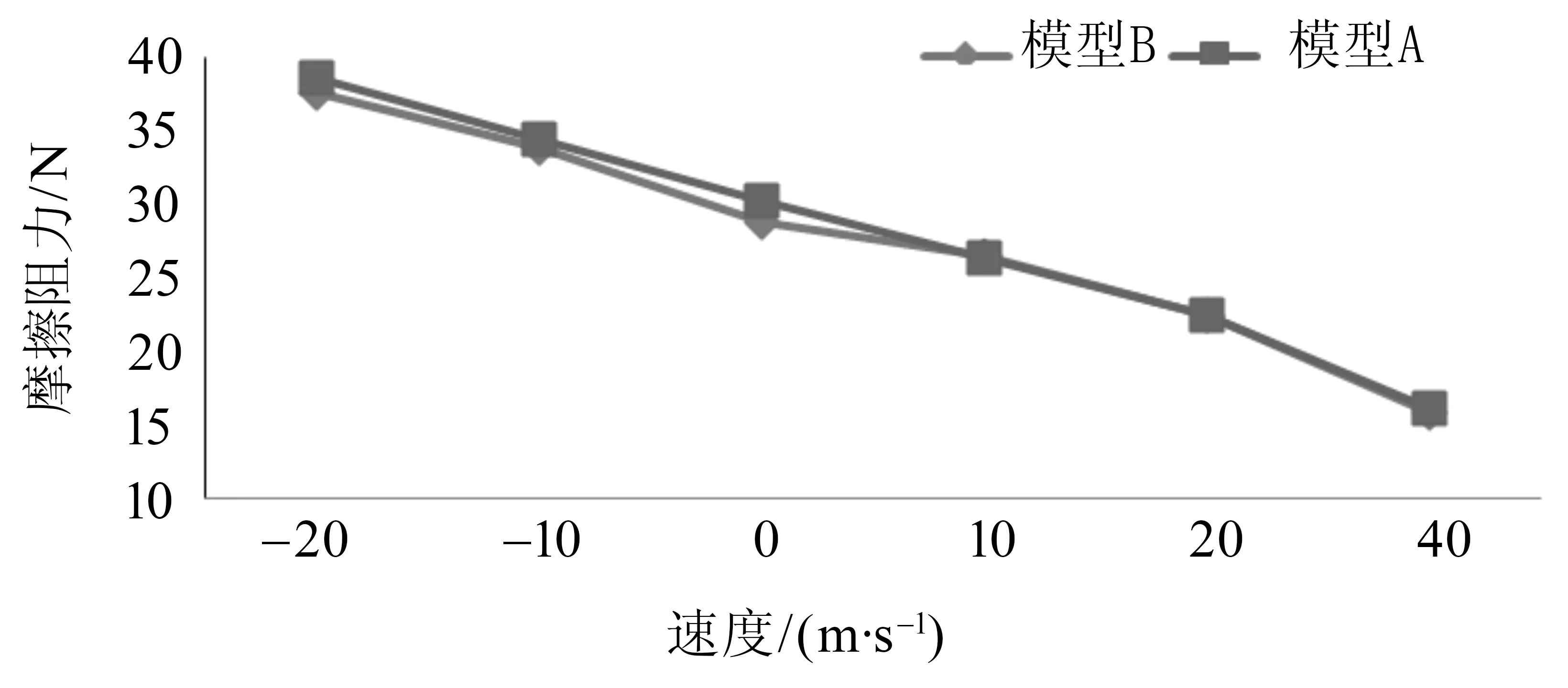
图6　不同工况下A、B模型的摩擦阻力变化曲线Fig.6　The viscous resistance changing curve of model A and B

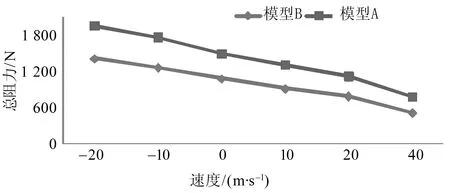
图7　不同工况下A、B模型的总阻力变化曲线Fig.7　The total resistance changing curve of model A and B

图5-7分别表示A、B模型在不同工况下的压差阻力、摩擦阻力和总阻力变化情况。由图可知，A、B模型由静止工况(速度为0)开始，逆流行驶时，压差阻力、摩擦阻力和总阻力随着行驶速度的增加而增大，并且两模型的阻力差逐渐变大；而顺流行驶时，阻力则随着行驶速度的增大而减小，并且两模型的阻力差逐渐减小。此外，在速度变化的过程中A模型受到的阻力一直大于B模型所受到的阻力。

3.3　表面压强分析

由表5-6可知，从工况1至6，A、B两种机器人的表面压强是递减的。同一工况下，负压的绝对值比正压大；随着速度的变化，负压变化的程度也比正压剧烈。总体上，B模型的表面压强大于A模型，但随速度变化波动小；二者的正压强相差不大，约为8 ～ 547 N；而负压强相差较大，约为329 ～ 891 N；且， A、B模型的压强差随速度增大而增大。

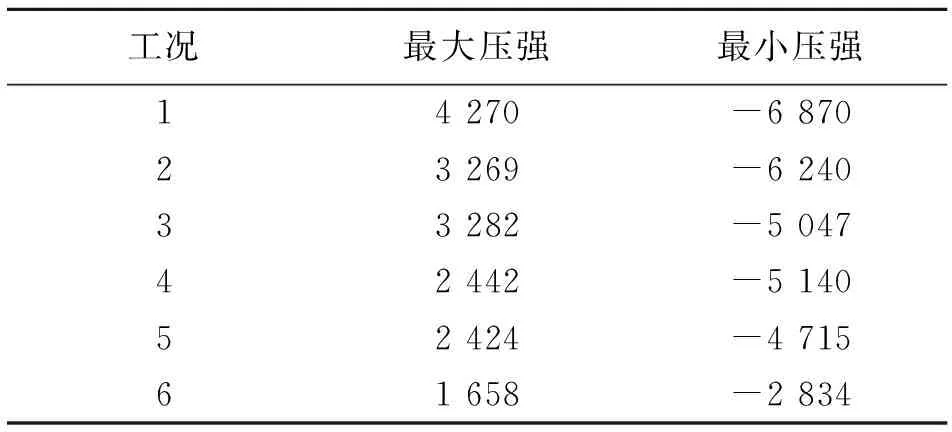
表5　不同工况下A模型压强值Table 5　Pressure analysis of model A 　Pa

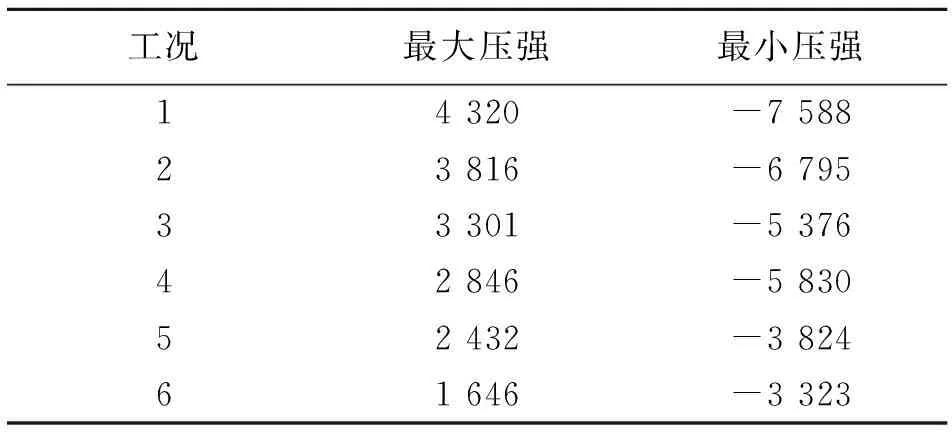
表6　不同工况下B模型压强值Table 6　Pressure analysis of model B 　Pa

3.4　流场分析

工况1、3和5下，A、B两种机器人周围流场的流速分布如图8-13所示。图8-13分别反映了不同前端支撑结构的机器人在逆流行驶20 m/min(工况1)、静止(工况3)和顺流行驶20 m/min(工况5)3种工况下周围流场的流速分布和尾流特征。总体来说，A、B模型的流速分布差异不大，前端支撑结构对于流场的影响较小。

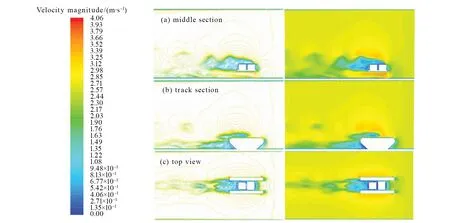
图8　工况1模型A各截面的流速分布图Fig.8　Velocity distribution of different sections of model A under condition 1

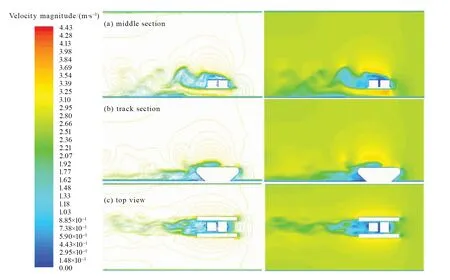
图9　工况1模型B各截面的流速分布图Fig.9　Velocity distribution of different sections of model B under condition 1

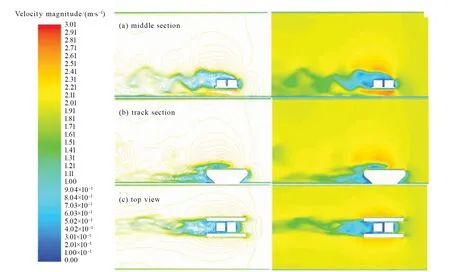
图10　工况3模型A各截面的流速分布图Fig.10　Velocity distribution of different sections of model A under condition 3

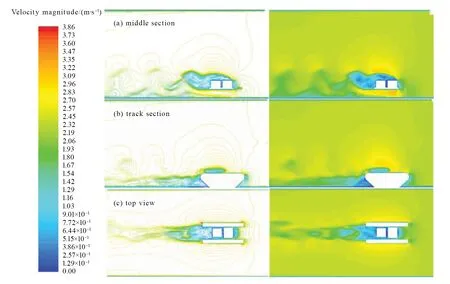
图11　工况3模型B各截面的流速分布图 Fig.11　Velocity distribution of different sections of model B under condition 3

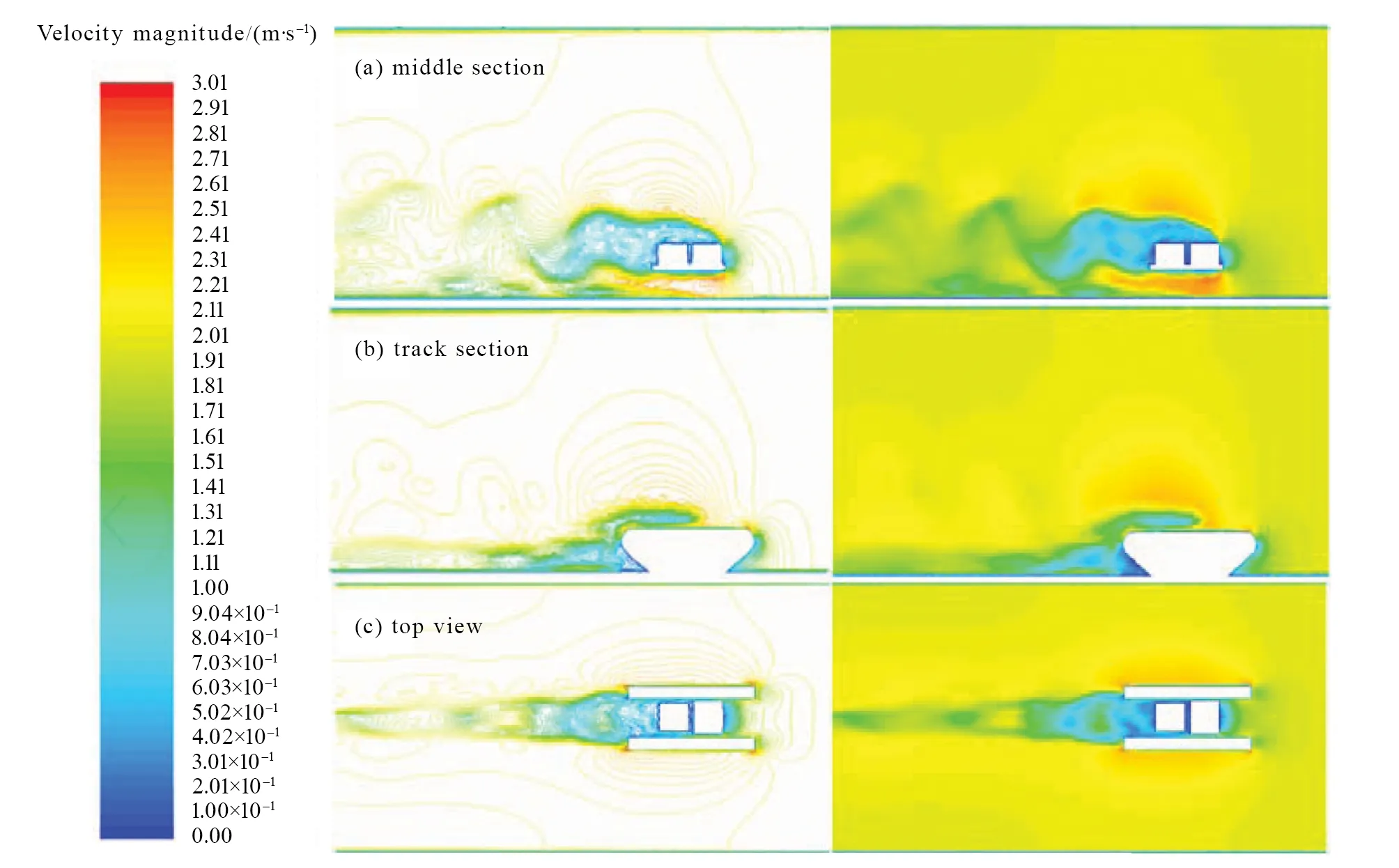
图12　工况5模型A各截面的流速分布图Fig.12　Velocity distribution of different sections of model A under condition 5

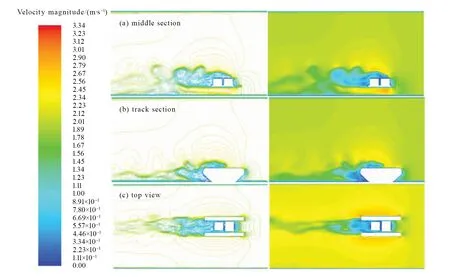
图13　工况5模型B截面流场流速分布图Fig.13　Velocity distribution of different sections of model B under condition 5

如图8-13中(a)所示，三种工况下两种机器人均在其后端尾迹区出现流线密集、流场混乱的情况，并伴随着流动分离现象。且，这种现象随着速度的增大呈现出加强的趋势，导致机器人承受的阻力增大，不利于机器人在水下行驶和工作。同时，A模型尾迹区的波动程度要大于B模型的，这与阻力分析的结果相吻合。

由图8-13中(b)可知，在履带后方垂直来流方向上会出现一块速度为零的区域，使得机器人在水下行驶时出现负压。且，顺流行驶时的负压压强小于逆流行驶情况下的，但二者的负压区域范围相差不大。而，B模型的负压区域比A模型的略大一些，且形状较规则；在负压区域内B模型的速度也比A模型的小，这解释了压强分析中B模型的负压值比A模型的大，且随速度变化较稳定的现象。

由图8-13中(c)可知，沿来流方向在机器人后方的尾迹区域内同样存在流动分离、尾流的周期性涡脱落和旋转的现象，并可观察到近似的卡门涡街现象。该现象的不规则和混乱程度会随着速度的增加而加剧，但影响区域会减小。对比三种工况的流速分布，可以发现模型B的涡街范围和流场混乱程度要优于模型A的。

4　结　论

本文对比了不同支撑结构的水下机器人的水流阻力、表面压强和流场流速分布，分析了不同工况下阻力和表面压强的变化规律及影响因素。主要结论有：

1)机器人的支撑结构对机器人所承受阻力和表面压强有明显的影响。杆件前端支撑结构可减小水下机器人所承受的水流阻力(约30%)，并且能降低表面压强随速度的波动。

2)水流总阻力分为压差阻力和摩擦阻力。其中，压差阻力在水流阻力中占主导地位(约占97%)，而摩擦阻力所占比例很小。A模型在工况1-6的阻力分别为：1 972.557、1 780.408、1 508.515、1 315.489、1 129.324和785.163 N；B模型在工况1-6的阻力分别为：1 425.777、1 276.545、1 089.851、916.507、791.152和516.836 N。由此可以得出，顺流时阻力随着速度的增加而降低；在逆流时阻力则呈现出相反的变化趋势，即随着速度增加而增加。

3)水下机器人在工作环境中存在负压区，负压区集中在履带后方。A模型的机器人在工况1-6的表面压强分别为：4 270、3 269、3 282、2 442、2 424和1 658 Pa；B模型的机器人在工况1-6的表面压强分别为：4 320、3 816、3 301、2 846、2 432和1 646 Pa。可以看出，顺流时表面压强随着速度的增加而降低；逆流时则相反，与阻力的变化规律相似。

4)通过对机器人周围流场的分析发现：前端支撑结构对于水下机器人的流场影响较小，两模型的机器人在不同工况下的流速分布基本相同。水下机器人尾部承载结构附近边界层分离现象严重，均出现了近似的卡门涡街现象，不利于机器人的稳定行驶和工作。而，通过对比可以发现B模型的边界层分离现象要略优于A模型，即杆件结构优于板件。

致谢:本项目获得国家自然科学基金(11572356)和NSFC-广东联合基金(第二期)超级计算科学应用研究专项资助。

参考文献：

[1]王玉婷, 向先波, 王瑟. 基于CFD和直接计算技术的航行器阻力系数算法研究 [J]. 中国科技论文, 2016, 11(19) : 2164-2168.

WANG Yuting, XIANG Xianbo, WANG Se. A study on hydrodynamic drag coefficients of underwater vehicles based on CFD and direct calculation methods [J]. China Sciencepaper, 2016, 11(19) : 2164-2168.

[2]王妹婷, 齐永锋, 汤方平，等. 水下机器人外形优化设计 [J]. 机床与液压, 2014, 42(5) : 76-79.

WANG Meiting, QI Yongfeng, TANG Fangping, et al. Shape optimal design of underwater robot [J]. Machine Tool & Hydraulics, 2014, 42(5) : 76-79.

[3]于宪钊, 苏玉民, 王兆立，等. 微小型水下机器人阻力性能的数值模拟 [C] ∥ 颜开. 中国造船工程学会学术论文集: 船舶水动力学学术会议暨中国船舶学术界进入ITTC30周年纪念会论文集. 杭州: 《中国造船》编辑部, 2008: 132-136.

[4]刘玉秋, 于开平, 张嘉钟. 水下非流线型航行体减阻的数值模拟与比较 [J]. 工程力学, 2007, 24(2) : 178-182.

LIU Yuqiu, YU Kaiping, ZHANG Jiazhong. Numerical simulation and comparison on drag reduction of Non-Streamline submerged body [J]. Engineering Mechanics, 2007, 24(2) : 178-182.

[5]NEMATOLLAHI A, DADVAND A, DAWOODIAN M. An axisymmetric underwater vehicle-free surface interaction: a numerical study [J]. Ocean Engineering, 2015 (96) : 205-214.

[6]谷海涛, 林扬, 胡志强. 带槽道桨水下机器人阻力特性的数值分析 [J]. 微计算机信息, 2007 (23) : 227-229.

GU Haitao, LIN Yang, HU Zhiqiang. Numerical analysis on the resistance of autonomous underwater vehicle with tunnel thruster [J]. Microcomputer Information, 2007 (23) : 227-229.

[7]周晗, 谢海斌, 徐海军,等. 基于CFD的水下机器人载体形体阻力优化设计 [C] ∥ 陈宗海. 系统仿真技术及其应用: 系统仿真技术及其应用学术会议论文集. 合肥: 中国科学技术大学出版社, 2009: 62-66.

[8]韩晓东, 王坚茹, 孟秀清. 水下航行体几何外形对阻力影响的数值模拟 [J]. 机械, 2011, 38(9) : 15-18.

HAN Xiaodong, WANG Jianru, MENG Xiuqing. Underwater navigation body numerical simulation of influence on the resistance [J]. Machinery, 2011, 38 (9) : 15-18.

[9]ZHANG Huaixin, PAN Yucun. Resistance performance of a dish-shaped underwater vehicle [J]. Journal of Shanghai Jiaotong University, 2006, 40(6) : 979-987.

[10]杨放琼, 谭青, 彭高明. 不确定环境下集矿机环境感知与实时避障研究 [J]. 中山大学学报(自然科学版), 2010, 49(4) : 58-62.

YANG Fangqiong, TAN Qing, PENG Gaoming. Research on environmental awareness and real-time obstacle avoidance of collector under uncertain environment [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2010, 49(4): 58-62.

[11]GEORGIADES C, NAHON M, BUEHLER M. Simulation of an underwater hexapod vehicle[J]. Ocean Engineering, 2009, 36(9) : 39-47.

[12]桑恩方. 用水下机器人进行堤坝安全隐患检测 [C] ∥ 石磊. 泄水建筑物安全及新材料新技术应用: 泄水建筑物安全及新材料新技术应用论文集. 海口: 中国水利技术信息中心, 2010: 121-125.

[13]孙丽. 自治水下机器人(AUV)三维结构设计及仿真分析 [D]. 青岛：中国海洋大学机械电子工程系, 2011.

[14]宋方希. 基于CFD的混合驱动水下航行器外形研究 [D]. 天津：天津大学机械工程系, 2012.

[15]YANG Xinping, XU Pengfei, HU Zhen. Research on visual simulation system of deep-sea vehicle [J]. Ocean Engineering, 2012, 30(1) : 137-144.

[16]马尧, 赵宏伟. 基于CFD的仿生机器鱼数值仿真分析 [J]. 白城师范学院学报, 2014, 28(5): 13-18.

MA Yao, ZHAO Hongwei. Numerical simulation analysis of bionic robot fish based on CFD [J]. Journal of BaiCheng Normal University, 2014, 28 (5): 13-18.

[17]LIU Guijie, CHEN Gong, JIAO Jianbo, et al. Dynamics modeling and control simulation of an autonomous underwater vehicle [J]. Journal of Coastal Research, 2015 (73) : 741-746.

[18]郭丙华, 李中华. 基于障碍物地平角点的移动机器人定位 [J]. 中山大学学报(自然科学版), 2013, 52(5) : 45-50.

GUO Binghua, LI Zhonghua. A method of localization for mobile robot based on obstacle-ground-corner [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2013, 52(5) : 45-50.

[19]王黎阳. 潜水机器人在深孔有压式隧洞环境检测中的应用 [J]. 大坝与安全, 2015 (3) : 55-58.

WANG Liyang. Application of diving robot in deep hole pressure tunneling [J]. Dam & Safety, 2015 (3) : 55-58.

[20]PARK S W, KIM M S, SOHN J H, et al. Study on the fluid resistance coefficient for control simulation of an underwater vehicle [J]. The Korea Society for Power System Engineering, 2016, 20 (1) : 24-29.

[21]刘源, 凌杰, 陈家旺. 基于Fluent的水下步行机器人结构优化设计 [J]. 中国水运, 2017, 17(1) : 125-128.

LIU Yuan, LING Jie, CHEN Jiawang. Optimal design of underwater pedestrian robot structure based on fluent [J]. China Water Transport, 2017, 17 (1): 125-128.

[22]张爽, 邬依林, 葛伟亮, 等. 仿人服务机器人的平衡控制 [J]. 中山大学学报(自然科学版), 2016, 55(5) : 14-20.

ZHANG Shuang, WU Yilin, GE Weiliang, et al. Balance control of a humanoid service robots [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2016,55 (5): 14-20.

[23]王福军. 计算流体动力学分析——CFD软件原理与应用 [M]. 北京：清华大学出版社, 2004：272.

WANG Fujun. Computational fluid dynamics analysis-principles and applications of CFD Software[M]. Beijing: Tsinghua University Press, 2004: 272.

[24]胡文清, 詹杰民. 一种在FluentUDF中使用IMSLFortran数值库的方法 [J]. 中山大学学报(自然科学版), 2017, 56(3) : 31-35.

HU Wenqing, ZHAN Jiemin. A method of using IMSL Fortran numerical libraries in Fluent UDF [J].Acta Scientiarum Naturalium Universitatis Sunyatseni, 2017, 56 (3) : 31-35.

[25]张楠, 沈泓萃, 姚惠之. 潜艇阻力与流场的数值模拟与验证及艇型的数值优化研究 [J]. 船舶力学, 2005, 9(1) : 1-13.

ZHANG Nan, SHEN Hongcai, YAO Huizhi. Numerical simulation and verification of submarine resistance and flow field and numerical optimization of hull shape [J]. Journal of Ship Mechanics, 2005, 9 (1): 1-13.

[26]汪小翔, 许靖峰, 李徐, 等. 艇模水下阻力试验方法研究与数值验证 [J]. 舰船科学技术, 2016, 38(4) : 42-46.

WANG Xiaoxiang, XU Jingfeng, LI Xu, et al.Study on the underwater resistance test method and numerical verification of the jets [J]. Ship Science and Technology, 2016, 38 (4): 42-46.

[27]陈小邹. 翼型附体与平板交接部流场分析 [J]. 舰船科学技术, 2010, 32(10) : 8-11.

CHEN Xiaozou. Flow field analysis of airfoil attached to flat plate [J]. Ship Science and Technology, 2010, 32(10) : 8-11.

[28]常煜, 张志荣, 赵峰. 多块结构化网格在含附体水面船模粘性流场数值计算中的应用 [J]. 船舶力学, 2004, 8(1) : 19-25.

CHANG Yu, ZHANG Zhirong, ZHAO Feng. Application of multiple structured grids to numerical simulation of viscous flow field in surface ship with attached body [J]. Journal of Ship Mechanics, 2004, 8 (1): 19-25.