洪水峰量联合分布的4种重现水平对比*
2018-04-02陈子燊刘占明赵青
陈子燊,刘占明,赵青
(1.中山大学地理学院,广东 广州 510275;2.佛山科学技术学院,广东 佛山 528000;3.中山市南区水利所,广东 中山 528455)
政府间气候变化专门委员会(IPCC)第5次评估报告预测气候变化会增大包括洪涝在内的各种水文极端事件发生的概率,此对江河堤围和水库大坝等水利工程设施将造成严重威胁。如何评估变化环境下水文极端事件的风险并提出相应的设计标准是应对洪涝灾害的重要科学与工程应用问题。洪水过程是由洪峰流量、洪水总量和洪水历时等多个特征要素有机组成的一个整体,至今对多变量洪水频率分析已经有较多的研究[1-5],文献[6]对此作了述评。李天元等[7]认为目前大多数研究还限于在构建多变量洪水联合分布的基础上进行联合重现期和条件概率的分析。郭生练等[8]进一步指出,对于给定的重现期水平,存在无穷多种满足防洪标准的洪峰、洪水总量组合,如何合理地选择设计值是关键问题,如何在多变量框架下进行洪水联合设计值估算和风险评估仍然是一个有争议的问题,应加强这方面的研究。
至今,“或”和“且”重现期是最常用的两种多变量重现期定义方法,但在安全与危险事件的判定上两者都存在着较大局限性[9]。Salvadori等[10]针对“或”重现期的不足提出了划分安全与危险临界域的新多变量重现期——Kendall重现期(Kendall return periods,KRP。又称二次重现期,secondary return periods),其相关原理已在海岸工程设计研究中得到了初步应用[11-12]。随后,进一步针对“且”重现期的不足,基于生存Kendall分布函数,提出了划分安全与危险的临界域的新多变量重现期—生存kendall重现期(survival Kendall return periods,SKRP)[13]。本文拟通过实例对比分析 “或”首次重现期和二次重现期的联合设计水平、“且”首次重现期和生存Kendall重现期的联合设计水平之间的差异,希翼有助于深化对洪水风险的认识,为防洪设计标准提供新的参考。
1 理论与方法
1.1 Copula函数与首次重现期
根据Sklar定理,若F(·)是一个二维随机变量(X,Y)的累积分布函数,其边缘分布函数是连续函数u=FX(x),v=FY(y),则有唯一的Copula函数C使得:
F(x,y)=P(X≤x,Y≤y)=
C(FX(x),FY(y))=C(u,v)
(1)
(2)

(3)
“或”重现期和“且”重现期也统称为首次重现期(primary return periods)。
1.2 Kendall分布函数与Kendall重现期
从首次重现期可知,不同的u、v组合只要其出现累积概率(记为t)相同都可产生相同的重现期。针对“或”首次重现期定义的安全域/危险域存在误判的问题,Salvadori等[10]利用Nelsen[14]定义的Kendall分布函数划分出亚临界(安全域)、临界(警戒事件)和超临界(危险域)3种情景。通过判定累积概率是否小于或等于某临界概率t,将多维的极值事件投射为一维分布。则基于Copula函数累积概率为t的(u,v)组合值,Kendall分布函数KC为[15]:
KC(t)=t-φ(t)/φ′(t),0 (4) 式中,φ′(t)为φ(t)的右导数。由Kendall分布函数确定的重现期即Kendall重现期为: (5) (6) 定义TSK为生存Kendall重现期(survival Kendall return period,SKRP): (7) 多变量联合分布同一个重现期可以有不同的分位数组合与之对应,这些分位数组合无法通过概率分布的反函数直接计算。具有相同重现期Tp(C(u,v)=p)的分位值组合构成了一个二维点集(等曲线),设计分位数组合必然存在一个使联合概率密度f(u,v)达到最大值的组合(um,vm),即该组合出现的可能性最大。因此,在设定重现期条件下出现最大可能组合的设计值可作为工程设计与风险管控标准的合理选择。 (8) f(u,v)=c(u,v)f(u)f(v) (9) 式中,c为二维Copula的概率密度函数。 位于珠江三角洲河口区的增江是珠江流域三大干流之一东江的一级支流,河流全长203 km, 流域面积约3 160 km2。1954年设立的麒麟咀水文站是增江流量控制站和国家重要水文站,距河口距离33 km,集水面积2 866 km2。本研究采用麒麟咀水文站1954-2011年共58 a的逐日流量数据,按年最大值提取此水文站历年洪水的洪峰流量Q与同场洪水总量W作为研究样本。 采用水文频率分析中常用的3种三参数概率分布:皮尔逊三型分布(P-III)、广义极值分布(GEV)、对数正态分布(GNO)分别拟合洪峰流量、洪水总量和洪峰水位样本。参数估计使用线性矩(L-矩)方法。经验频率分布使用Gringorten公式。拟合结果采用均方根误差(RMSE)、和概率点据相关系数(PPCC)检验其拟合优度。如表1所示,洪峰流量序列选用GEV分布, 洪量序列选用P-III分布。 表1 洪峰和洪量的概率分布参数与拟合优度检验值Table 1 The parameters of the marginal distribution and the values of goodness of fit test 洪峰Q和洪量W的Kendall相关系数为0.565。采用相关性指标法计算Q-W联合分布的Gumbel-Hougaard copula、Frank copula、A-M-H copula和Clayton copula的参数θ及相应的AIC和OLS值,计算结果见表2。以OLS和AIC值最小,拟合度最高的二维Gumbel -Hougaard copula构建的洪水峰量联合分布的Copula模式如下: C(FQ(q),FW(w))= exp{-[(-lnFQ(q))2.299+ (-lnFW(w))2.299]1/2.299} (10) 表2洪水峰量联合分布的参数估计与拟合优度评价结果 ArchimedeanCopulaθOLSAICClayton2.5980.031-173A-M-H0.9900.047-152Gumbel-Hougaard2.2990.025-183Frank7.0550.028-178 分析某特定洪峰流量条件下,出现洪水总量的概率分布。当给定Q≥q时,W≥w的条件概率为: (11) 条件重现期为: (12) 从表3可看出:① 当麒麟咀洪峰流量大于等于某一特定频率设计值时,洪水总量出现大于等于该频率设计值的条件概率随着超值概率的减小而减小,以Q出现大于等于概率P1%时的设计洪峰流量Q=3 635 m3/s为例,洪水总量出现大于等于P10%、P5%、P2%、P1%、P0.5%和P0.2%的条件概率分别为0.981、0.950、0.836、0.651、0.417和0.189,其相应的条件重现期为:1.0、1.1、1.2、1.5、2.4和5.3 a。② 反之,洪量大于等于某一特定频率设计值时,洪峰流量出现大于等于该频率设计值的条件概率随着超值概率的减小而增大。如,百年一遇的设计洪量W=1 702×106m3,其与洪峰流量的遭遇随超值概率的减小而增大,洪峰流量出现大于等于P10%、P5%、P2%、P1%、P0.5%和P0.2%的条件概率分别为0.098、0.190、0.418、0.651、0.834、0.947,其相应的条件重现期为:10.2、5.3、2.4、1.5、1.2和1.1 a。此外,洪水峰量同频率遭遇的概率超过64.9%,表明二者遭遇的概率非常高。上述分析表明,可能存在着满足多种防洪标准的洪水峰量组合,需要合理地推算其设计值。 表3Q-W洪水组合条件概率 P(W≥w|Q≥q)或P(Q≥q|W≥w)W/Q2396278532763635398544369600.6720.8510.9540.9810.9920.99811890.4250.6600.8800.9500.9800.99414830.1910.3520.6530.8360.9310.97917020.0980.1900.4180.6510.8340.94719180.0500.0980.2330.4170.6490.87322000.0200.0400.0980.1890.3490.649 图1 P(W≥w|Q≥q)条件概率分布图Fig.1 Diagram of conditional probability distributions of joint distribution between flood discharges and volumes 按设定重现期(500、200、100、50、20和10 a)推算麒麟咀测站的洪峰流量和洪水总量单变量设计值,以出现概率最大的原理推算洪水峰量联合分布的“或”重现期、“且”重现期、Kendall 重现期和生存Kendall 重现期设计值列于表5。结果显示,对于设定的10 ~ 500 a重现期,按Kendall重现期推算的设计洪峰流量和设计洪水总量分别小于“或” 重现期设计值和边缘分布设计值,按Kendall重现期推算的洪峰流量和设计洪水总量设计值和相应边缘分布设计值的相对误差分别为-2.8% ~ -5.4%和-3.8% ~ -8.1%;推算的生存Kendall重现期设计洪峰流量和设计洪水总量分别大于“且”重现期设计洪水值和边缘分布设计值,生存Kendall重现期设计洪水值和相应的边缘分布设计值二者的相对误差分别为2.4% ~ 3.8%和0.3% ~ 4.8%。这一结果也表明,按目前有关规范设计要求的单变量洪水要素设计值已达到设计洪水安全标准,按洪水峰量联合分布的“或”重现期推算的洪水设计值存在高估问题,导致投入费用偏大,按洪水峰量联合分布“且”重现期推算的洪水设计值存在低估问题,可能增大防洪工程损毁风险。按洪水峰量联合分布的Kendall重现期或生存Kendall重现期推算的洪水设计值可为防洪工程安全与设计标准提供更坚实的理论依据。为了比较,进一步推算洪峰—洪量同频率分布设计值[16]: 表5 不同重现期下洪峰流量与洪水总量的设计值Table 5 Design values of flood discharges and flood volumes at different return periods u1=u2=[1-(1/Tu1,u2)]α; (13) 本文对比分析了增江流域麒麟咀断面洪峰洪量之间的二维联合分布及其4种重现水平,有以下结论: 1)对于预设的重现期,相对于“或”联合重现期,Kendall重现期可更准确地识别单个超临界区域的风险率;相对于“且”联合重现期,生存Kendall重现期可更好地描述洪峰洪量同时超阈值情况下的风险率。 2)按目前有关规范设计要求的单变量洪水要素设计值基本达到设计标准,按洪峰洪量“或”重现期和同频率推算的设计洪水分位数偏高,工程费用偏大,采用Kendall重现期和生存Kendall重现期推算的设计洪水值可为防洪工程风险管理与设计提供新的选择与参考。 参考文献: [1]冯平,毛慧慧,王勇.多变量情况下的水文频率分析方法及其应用[J].水利学报,2009,40(1):33-37. FENG Ping, MAO Huihui, WANG Yong. Method for hydrological reoccurrence frequency analysis under the condition of multivariate[J]. Journal of Hydraulic Engineering, 2009,40(1):33-37 . [2]ZHANG L, SINGH V P. Bivariate flood frequency analysis using the copula method [J]. Journal of Hydrologic Engineering, 2006, 11(2) :150-164. [3]熊立华,郭生练,肖义,等. Copula 联结函数在多变量水文频率分析中的应用[J]. 武汉大学学报(工学版), 2005,38(6):16-19. XIONG Lihua, GUO Shenglian, XIAO Yi, et al. Application of Copulas to multivariate hydrological frequency analysis[J]. Engineering Journal of Wuhan University, 2005, 38(6):16-19. [3]方彬, 郭生练, 肖义, 等. 年最大洪水两变量联合分布研究[J]. 水科学进展, 2008, 19( 4) : 505-511. FANG Bing, GUO Shenglian, XIAO Yi, et al. Annual maximum flood occurrence dates and magnitudes frequency analysis based on bivariate joint distribution[J]. Advances in Water Science,2008,19(4) : 505-511. [5]陈子燊, 黄强, 刘曾美. 基于非对称Archimedean copula与kendall分布函数的三变量洪水风险评估[J]. 水科学进展, 2016, 27(5):763-771. CHEN Zhisheng, HUANG Qiang, LIU Zengmei. Risk assessment of trivariate floods based on asymmetric copula and kendall distribution function[J]. Advances in Water Science,2016, 27(5):763-771. [6]郭生练,闫宝伟,肖义,等. Copula 函数在多变量水文分析计算中的应用及研究进展[J]. 水文,2008,28(3):1-7. GUO Sheng lian, YAN Baowei, XIAO Yi, et al. Multivariate hydrological analysis and estimation[J]. Journal of China Hydrology, 2008,28(3):1-7. [7]李天元,郭生练,刘章君,等. 基于峰量联合分布推求设计洪水[J].水利学报,2014,45(3):269-276. LI Tianyuan,GUO Shenglian,LIU Zhangjun,et al. Design flood estimation based on bivariate joint distribution of flood peak and volume[J]. Journal of Hydrologic Engineering,2014,45(3):269-276. [8]郭生练,刘章君,熊立华.设计洪水计算方法研究进展与评价[J].水利学报,2016,47(3):302-314. GUO Shenlian, LIU Zhangjun, XIONG Lihua. Advances and assessment on design flood estimation methods[J]. Journal of Hydraulic Engineering,2016,47(3):302-314. [9]SALVADORI G, de MICHELE C. Frequency analysis via copulas: theoretical aspects and applications to hydrological events[J]. Water Resources Research, 2004, 40(12):229-244. [10]SALVADORI G, MICHELE D C, DURANTE F. On the return period and design in a multivariate framework[J]. Hydrology and Earth System Sciences, 2011, 15: 3293-3305. [11]CORBELLA S, STRETCH D D. Multivariate return periods of sea storms for coastal erosion risk assessment[J]. Natural Hazards and Earth System Sciences, 2012, 12: 2699-2708. [12]SALVADORI G, TOMASICCHIO G R, ALESSANDRO F D. Multivariate approach to design coastal and off-shore structures[J]. Journal of Coastal Research, 2013, 65: 386-391. [13]SALVADORI G, DURANTE F, de MICHELE C. Multivariate return period calculation via survival functions[J]. Water Resources Research, 2013, 49: 2308-2311. [14]NELSEN R B. An introduction to copulas (springer series in statistics) [M]. New York: Springer,2006:216. [15]GRALER B, VANDENBERG M J, VANDENBERGHE S, et al. Multivariate return periods in hydrology: a critical and practical review focusing on synthetic design hydrograph estimation[J]. Hydrology and Earth System Sciences, 2013, 17(4): 1281-1296. [16]肖义, 郭生练, 刘攀, 等. 分期设计洪水频率与防洪标准关系研究[J].水科学进展, 2008, 19(1) : 54- 60. XIAO Yi, GUO Shenlian, LIU Pan, et al. Seasonal flood frequency analysis and flood prevention standard[J]. Advances in Water Science,2008,19(1) :54-60.1.3 生存Kendall函数与生存Kendall重现期


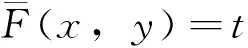
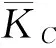
1.3 联合分布设计值
2 示例研究
2.1 基本数据
2.2 边缘分布与联合分布

Table 2Results of parameter estimation and goodness-of-fit tests for four Copulas
2.3 条件概率分布
Table 3Conditional probabilities ofQ-W

2.4 联合分布重现期和危险率
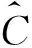
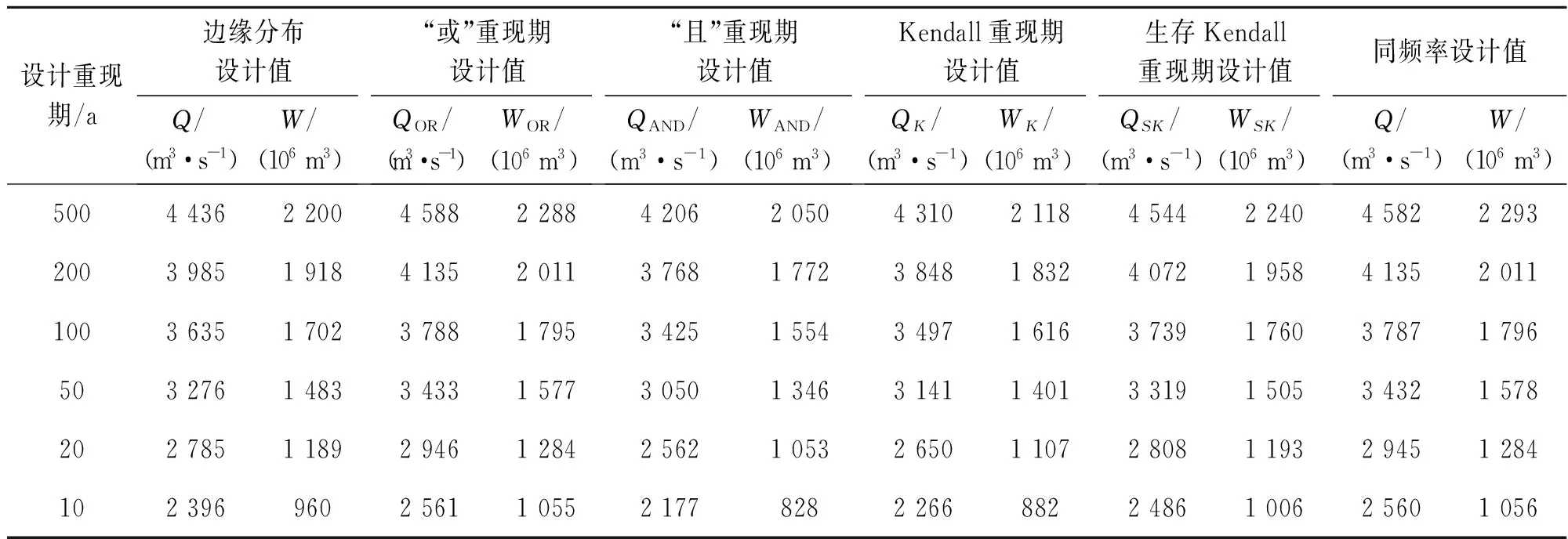
2.5 洪水设计值

3 结 论
