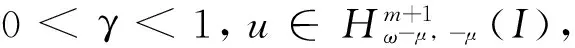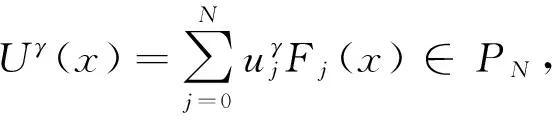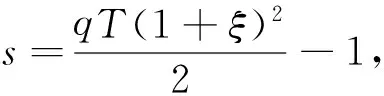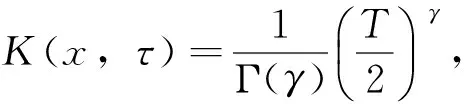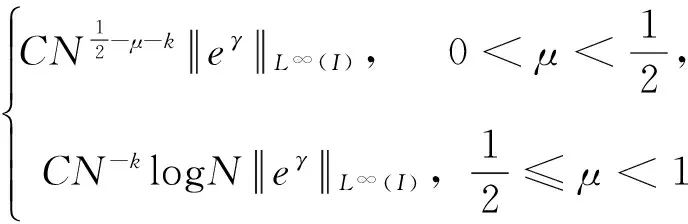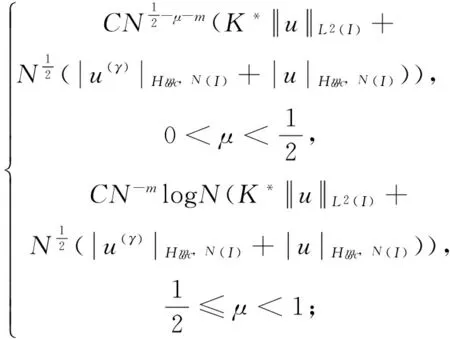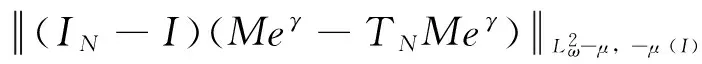带非线性延迟项的分数阶微分积分方程收敛性*
2018-04-02郑伟珊
郑伟珊
(韩山师范学院数学与统计学院,广东 潮州 521041 )
分数阶微分积分是关于任意阶微分和积分的理论,它与整数阶微分积分是统一的,是整数阶微分积分的推广。整数阶微分积分作为描述经典物理及相关学科理论的解析数学工具已为人们普遍接受,不少问题的数学模型最终都归结为整数阶微分积分方程的定解问题, 其无论在理论分析还是数值求解方面都已有较完善的理论。但当进入到复杂系统和复杂现象的研究时,经典整数阶微分积分方程对这些系统的描述将遇到困难,而分数阶微分积分方程因更好地刻画和描述了自然现象、动态系统的变化过程而得到了广泛的应用,比如在金融领域,分数阶微分积分方程可用于描述长时间极限时的对数价格,可以更好的表现在长时间区间上价格的自然变动[1];在医学成像领域,Hall等[2]指出了MRI数据在复杂环境如人脑组织环境中的反常扩散现象,并用一类分数阶微分积分方程进行了模拟;国内学者王瑞萍等[3]研究分数阶PD 速度控制器的永磁同步电动机控制问题。此外分数阶微分积分方程也已经被成功应用于生物、物理、化学、水文、环境等方向,因此发展分数阶微分积分方程的理论及给出相应的数值方法具有广阔的应用前景。
目前已有几种求解分数阶微分积分方程的方法,包括外推法[4]、配置法[5]和Adomian分解方法[6], 但是只有少数运用数值求解分数阶微分积分方程的方法,其中大多数是用有限差分方法,而这些通常都局限于低维度和有限精度的范围。近年来谱方法因其高精度受到了广泛的关注。关于谱方法的文献不少,上海大学郭本瑜等[7]创建了在非均匀Jacobi权Sobolev空间中Jacobi逼近的正交投影和配置理论,这对谱方法中的数值误差估计分析具有重要的作用。香港汤涛等专家提供了大量基本的谱算法及相应的收敛性及误差分析理论,这些常应用于实际中的线性和非线性问题。陈艳萍教授等提出了用Jacobi谱配置法求解了一类弱奇性Volterra积分方程,还用Legendre谱配置法求解具有光滑核的第二类Volterra积分方程,严格证明该方法误差呈谱精度收敛,并且近年也将这些方法延拓至分数阶微分积分方程[8-9],其中的分数阶导数为Caputo导数,无独有偶丁金凤等也研究基于Caputo 导数下的含时滞的Hamilton 系统的分数阶Noether 理论[10]。本文所讨论的分数阶微分积分方程,其导数和积分分别为Caputo分数阶导数和Riemann-Liouville分数阶积分,具体为:
(1)
(2)
其中t∈ [a,b],Γ(·)为Gamma函数,n为任意正整数且n- 1 <γ (3) 下面给出本文所研究的方程形式: (4) (5) 相应的范数定义为: (6) (7) 下面对式(4)和式(5)进行变量代换,令 倘若再记 则有 (8) u(x)-u(-1)= (9) u(γ)(xi)= (10) u(xi)= (11) 对于方程(10)和方程(11),当xi很小时,对 几乎没有可以应用的信息,故要获得高阶精度特别困难,为此通过如下线性变换将两积分区间转化成固定区间[-1,1],令 (12) (13) 其中-1 ≤θ≤ 1,则方程(10)和方程(11)可以重记为: u(γ)(xi)= (14) (15) 下面应用高斯积分法则近似处理方程(14)和方程(15),首先对于方程(14),用legendre-Gauss积分法则(6)近似计算: u(s(xi,θk))ωk+g(xi) (16) 而相应方程(15)可近似为: (17) (18) U(s(xi,θk))ωk+g(xi)= (19) (20) 在这一节将介绍一些在对随后定理证明有帮助的引理,这里I= (-1,1)。 (21) 其中 (22) (23) (24) (25) (26) (27) (28) (29) (30) 证明因为 故有 再由引理4获得所要证明结论。 引理6[15-16]对于一个非负整数r和k∈(0,1),存在一个常数Cr,k>0,使得对于任意函数v∈Cr,k([-1,1])都存在一个多项式函数TNv∈PN,使得 (31) 引理7[17k∈(0,1),0 则对于任意函数v∈C([-1,1]),都存在一个正的常数C使得 引理8[18]对于每个有界函数v,都存在一个独立于v的常数C, 使得 引理9[19]对所有可测函数f≥0,当1 本节将进行收敛性分析,其目标是证明方程的精确解与逼近解以及精确导数与逼近导数之间的误差均呈指数收敛。首先将L∞(I)空间上的进行收敛性分析。 (32) (33) 其中N足够大,C是独立于N但依赖K(x,s)和μ的常数, (34) (35) 证明利用离散内积(23),令 (36) 因此数值方法(19)和(20)可以写为 (37) (38) 进一步可将式(37)化为: (39) 记误差函数e(x) =U(x) -u(x),eγ(x) =Uγ(x) -u(γ)(x),利用引理1, 有 |Ii,1(x)|≤ (40) 再由式(12)和式(13)知,式(39)和式(38)分别可以化为 (41) (42) (43) (44) 这里 J3(x)=INu(γ)(x)-u(γ)(x), 得 |eγ(x)|≤LqT(1+ξ)· (45) 故由引理5有 (46) 再由式(44)有 (47) 综上得 (48) (49) 下面对式(48)及式(49)右端逐项进行误差估计,首先利用引理3、式(40)和式(49),有 (50) 又由引理2中的式(25)有 (51) 再次利用引理2中的式(25),并令m=1,有 |J4|L∞(I)≤ (52) (53) 最后一个不等式,我们在以下情况下使用引理6 假设N足够大, 由式(50)-式(53),有 定理2如果定理1中给出的假设成立,且N足够大,则有 (54) (55) 这里k∈(0,γ),C是独立于N的常数,而 证明根据式(44)和式(45),利用引理5的结论和引理9广义的Hardy不等式有 (56) (57) 现在使用引理8,可得 (58) 再根据定理1(令m=1)的收敛结果,有 故 (59) 由引理2中的式(24)可以得到 (60) 对于J4(x)的估计,使用引理2中的式(24)并令m=1时,得 (61) 对于J5(x)的估计,借助引理6,引理7和引理8,且当k∈(0,1-μ)有 (62) 最后一个不等号利用定理1的收敛性结果,故当N足够大,联合式(56)-(57)、式(59)-(62) 即可得定理所要证明的结论(54)和(55),其中γ=1-μ。 参考文献: [1]MEERSCHAERT M M, SCALAS E. Coupled continuous time random walks in finance [J]. Physica A, 2006, 370(1): 114-118. [2]HALL M G, BARRICK T R. From diffusion-weighted MRI to anomalous diffusion imaging [J]. Magnetic Resonance in Medicine, 2008, 59(3): 447-455. [3]王瑞萍, 皮佑国. 基于分数阶PD速度控制器的永磁同步电动机控制研究[J]. 中山大学学报(自然科学版), 2013, 52(3): 34-39. WANG R P, PI Y G. Research on fractional-order PD speed controller for PMSM [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2013, 52(3): 34-39. [4]DIETHELM K, WALZ G. Numerical solution of fractional order differential equations by extrapolation [J]. Numerical Algorithms, 1997, 16(3/4): 231-253. [5]RAWASHDEH E A. Numerical solution of fractional integro-differential equations by collocation method [J]. Appl Math Comp, 2006, 176(1): 1-6. [6]SHAWAGFEH N T. Analytical approximate solutions for nonlinear fractional differential equations [J]. Appl Math Comp, 2002, 131(2/3): 517-529. [7]GUO B Y, WANG L L. Jacobi approximations in nonuniformly Jacobi-weighted Sobolev spaces [J]. Journal of Approximation Theory, 2004, 128(1): 1-41. [8]YANG Y, CHEN Y P, HUANG Y Q. Convergence analysis of the Jacobi spectral-collocation method for fractional integro-differential equations [J]. Acta Mathematica Scientia, 2014, 34B (3): 673-690. [9]YANG Y, CHEN Y P, HUANG Y Q. Spectral-collocation method for fractional Fredholm integro-differential equations [J]. Korean Math Soc, 2014, 51(1): 254-278. [10]丁金凤,金世欣,张毅. 基于Caputo导数下的含时滞的Hamilton 系统的分数阶Noether 理论[J]. 中山大学学报(自然科学版), 2016, 55(6): 79-85. DING J F, JIN S X, ZHANG Y. Fractional Noether theorems for Hamilton system with time delay based on Caputo dervitaves [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2016, 55(6): 79-85. [11]CANUTO C, HUSSAINI M Y, QUARTERONI A, et al. Spectral methods fundamentals in single domains [M]. Springer-Verlag, 2006. [12]WEI Y X, CHEN Y P. Convergence analysis of the spectral methods for weakly singular Volterra integro-differential equations with smooth solutions [J]. Adv Appl Math Mech, 2012, 4(1): 1-20. [13]MASTROIANNI G, OCCORSIO D. Optimal systems of nodes for Lagrange interpolation on bounded intervals. A survey [J]. J Comput Appl Math, 2001, 134(1): 325-341. [14]HENRY D. Geometric theory of semilinear parabolic equations [M]. Berlin: Springer-Verlag, 1989. [15]RAGOZIN D L. Polynomial approximation on compact manifolds and homogeneous spaces [J]. Trans Amer Math Soc, 1970, 150(1): 41-53. [16]RAGOZIN D L. Constructive polynomial approximation on spheres and projective spaces [J]. Trans Amer Math Soc, 1971, 162(NDEC): 157-170. [17]COLTON D, KRESS R. Inverse acoustic and electromagnetic scattering theory ∥Applied mathematical sciences[M]. 2nd ed. Heidelberg: Springer-Verlag, 1998. [18]NEVAI P. Mean convergence of Lagrange interpolation: III [J]. Numerische Mathematik, 1991, 43(1): 195-218. [19]KUFNER A, PERSSON L E. Weighted inequalities of Hardy type [M]. New York: World Scientific, 2003.
1 Jacobi配置方法
1.1 配置点的设置

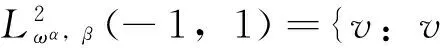




1.2 积分区间的转换
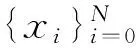


1.3 运用高斯求积公式求近似解



2 基本引理




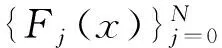


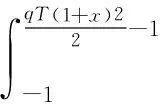




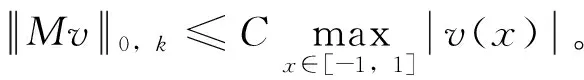
3 收敛分析