CCM Buck-Boost变换器非线性PID最优控制
2018-03-30兰志勇陈礼俊
兰志勇 陈礼俊 焦 石 李 理 王 波
(湘潭大学信息工程学院,湖南 湘潭 411105)
功率开关变换器是一类典型的通过控制其开关管开通与关断来实现电压变换的非线性系统[1-2]。由于其非线性特性,线性控制理论在此类系统中的应用具有较大的局限性,例如:系统动态响应与控制精度,因此线性控制理论不适用于开关变换器的分析与设计。研究新型非线性控制技术,从根本上解决线性控制理论在功率开关变换器上的不足十分重要[2-3]。
近 30年来非线性控制理论在应用研究领域取得了很大的进展,尤其以微分几何为工具发展起来的精确线性化方法受到了普遍重视[1-3]。精确线性化方法利用反馈变换以及精确非线性状态变换,实现输入-输出或输出-状态精确线性化,从而将复杂的非线性系统综合问题转化为线性系统综合问题[4-5]。该方法在线性化的过程中并没有像泰勒展开式一般忽略局部高阶非线性项,而是定义整体,因此该方法不仅精确而且适用于整个区域。由文献[1-5]可知,该方法已经被成功地用于解决一些实际控制问题。
就目前研究现状来看,在电力电子中应用微分几何理论的反馈线性化非线性控制方法,建立非线性系统的精确数学模型,未考虑实际系统的不确定性,鲁棒性不强[1-2,5]。因此为提高系统的鲁棒性,在实际应用中通常将该理论与无源控制、PI控制、滑模变结构控制等结合使用。
基于以上分析,本文以Buck-Boost变换器为研究对象,结合文献[6]中所提控制策略,由文献[6]可知,该文所提出控制策略能较好的改善 Boost变换器静态动态性能,但是所提控制策略从未应用于Buck-Boost变换器,因此本文将其结合并加以利用,用以改善Buck-Boost变换器非线性系统的静态动态性能。首先利用状态平均法建立起适用于微分几何方法的仿射非线性系统标准型,然后利用非线性坐标变换,将原有的仿射非线性系统转换成可控的线性系统,最后结合 PI控制构造非线性PI反馈律,实现对输出状态变量的控制。该策略一方面可以利用PI控制提高整个控制系统的鲁棒性;一方面精确反馈线性化则有助于改善其系统的动态特性。利用仿真工具,将非线性PI最优控制与传统 PI控制相比较,证实了该策略的优良的动态响应特性和强鲁棒性。
1 CCM Buck-Boost变换器仿射非线性系统模型
目前PWM型DC/DC变换器建模,常用的方法为状态空间平均建模法。依据平均建模法,图 1Buck-Boost变换器状态空间平均模型为
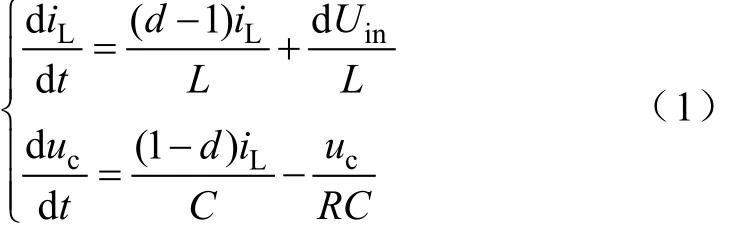
式中,d为占空比。选取状态变量X=[x1,x2]=[iL, uc],输入变量u(t)=d,输出变量y=h(X)=x2−Uref,可得到适用于微分几何的CCM Buck-Boost变换器的单输入单输出的仿射非线性控制系统:
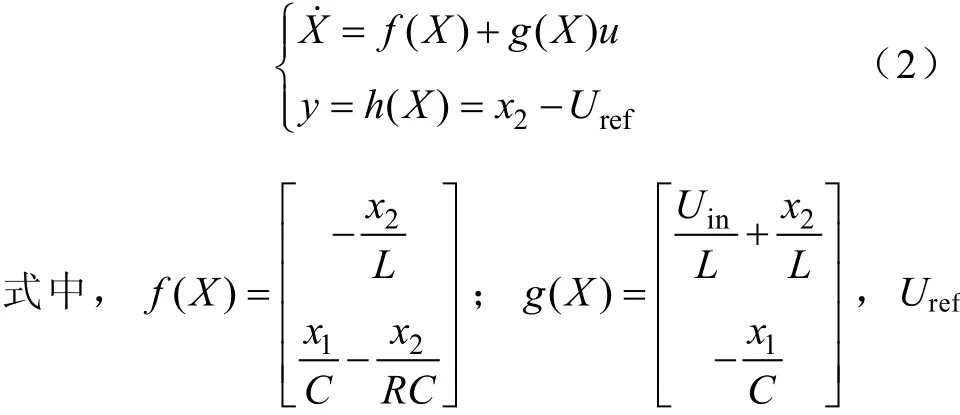
为需要输出的参考量。
2 变换器非线性控制系统设计
2.1 精确线性化最优控制
依据微分几何理论,文献[5,7]中详细证明式(2)所表示的仿射非线性控制系统满足系统精确化条件,但单输入单输出的仿射非线性控制系统相对阶r<系统的维数n,需要重新构造输出函数y=ω(X),使其满足系统相对阶条件。重新构造输出函数ω(X)必须满足:
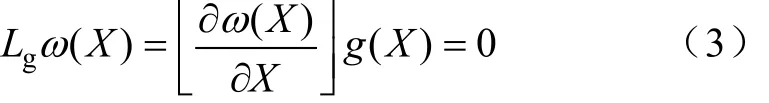
求解上述微分方程得多解,依据能量守恒定律,选择其中一解:
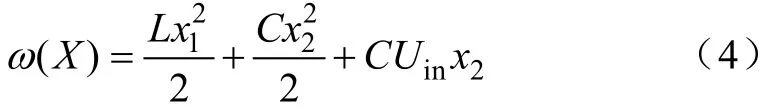
根据ω(X)构造坐标变换可计算:
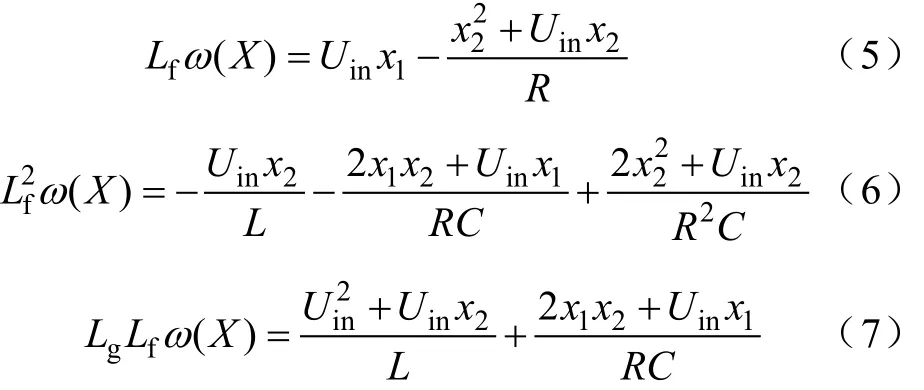
因此可取坐标变换:
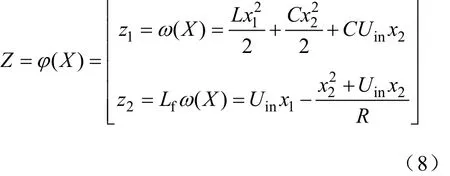
在新坐标下布鲁洛夫斯基标准型为
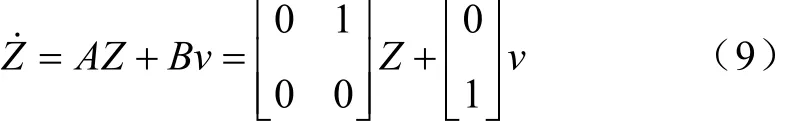
式中,z1、z2为变换后线性系统的状态变量;v为控制变量;u与v的关系式:

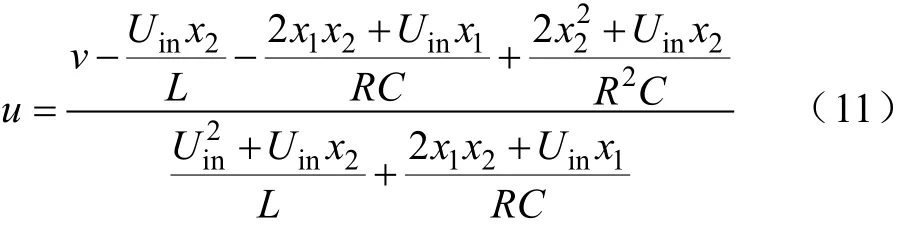
其中:
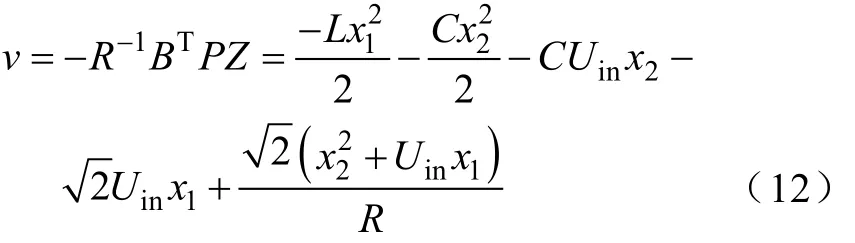
2.2 非线性PI反馈律设计
由以上分析可以得出通过所构建的虚拟函数,原仿射非线性系统转化为完全可控的线性系统。在实现原仿射非线性系统精确线性化的前提下,引入输出参考量Vref,实现PI控制电压输出,即构建具有非线性调节功能的PI控制环节[6,8-9]。其中非线性反馈坐标变换中的状态变量(ic、x2)由误差的比例积分过程来产生,kp、ki分别为 PI控制器参数,其参数的整定采用幅相裕度补偿法。
PI控制器设计具体步骤为:首先根据变换器系统参数,应用变换器开环传递函数式(13)计算被控对象数学模型;然后依据最小相位系统理论进行补偿,计算系统的PI参数稳定域;获得的参数稳定域后,经多次仿真测试确定最优PI控制器参数。求得 PI最优参数为:kp=0.001,ki=1。式(13)中 d为占空比,uo为输出电压。
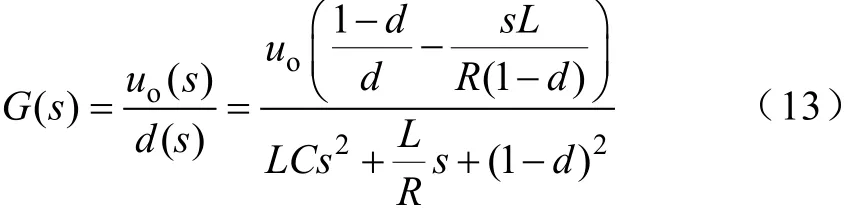
本文采用 Buck-Boost变换器非线性 PI最优控制策略,在线性PI控制向量中对输出误差的扰动先予以补偿,然后利用非线性最优控制组合出高品质控制器[6]。该方法结合了精确反馈线性化非线性控制与PI控制的优点,一方面利用PI调节对于干扰的不变性,提高整个系统的鲁棒性;另一方面精确线性化有利于建立PI控制,改善系统动态响应特性。其系统控制与如下。
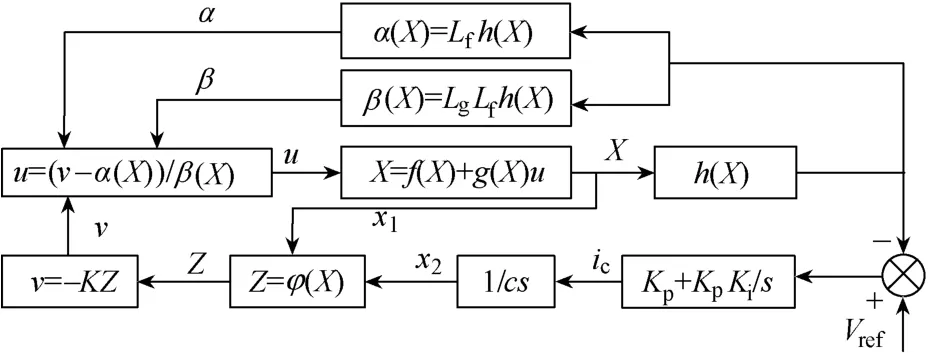
图2 变换器系统整体控制框图
3 系统仿真与实验
3.1 数值仿真参数
为了验证所采用的方法的正确性和优越性,利用 Matlab对系统进行数值仿真,并与传统PI控制方法进行对比分析,结果表明所提控制方法具有优越的动态性能和良好的鲁棒性。系统仿真参数如下:输入电压Uin=30V,输出电压Uout=40V,负载R=20Ω,开关频率fs=100kH,输入电感L=2mH,输出电容C=50μF,PI控制器的参数:kp=0.001,ki=1。
3.2 起动响应特性
图3分别是传统PI控制与非线性PI最优控制的起动电压波形对比图与起动电流波形对比图。比较分析可知,非线性PI最优控制能在极短的时间内跟踪到给定电压值,且没有超调,稳定后纹波小;同样电感电流起动亦具有相同的优点。
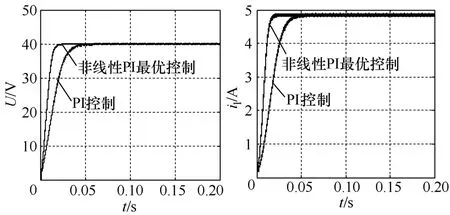
图3 输出电压和起动电感电流波形对比图
3.3 稳态特性
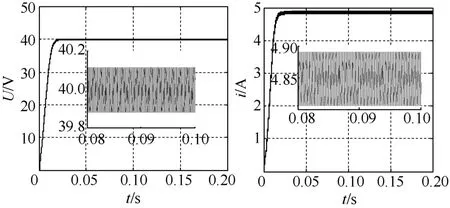
图4非线性PI最优控制控制下的稳态特性
图4 分别为非线性PI最优控制控制下电感电流与输出电压的稳态特性波形图,以及在开关周期内的细化图。系统稳定运行时,由图4可知电压稳定输出为x2=uo=40V,电流稳定输出为x1=iL=4.85A。输出电压与电感电流基本上在很小的范围内波动,具有较好的稳态特性。
3.4 负载扰动下动态响应
图5为负载由15Ω跳变到20Ω时两种控制策略的动态响应曲线。其中图5(a)为两种控制策略下,负载电阻突变时输出电压对比波形图。图5(b)为两种控制策略下,负载电阻突变时变换器电感电流对比波形图。由图5可知,在非线性PI最优控制策略下电感电流在负载电阻突变时能迅速响应,并稳定在新的稳态值,超调量小、无振荡过渡过程,变换器输出电压虽在负载电阻突变的瞬间存在一定的超调大约为5V,但很快恢复到设定的参考电压。与PI控制对比可知,本控制系统对负载变化具有更强的鲁棒性。
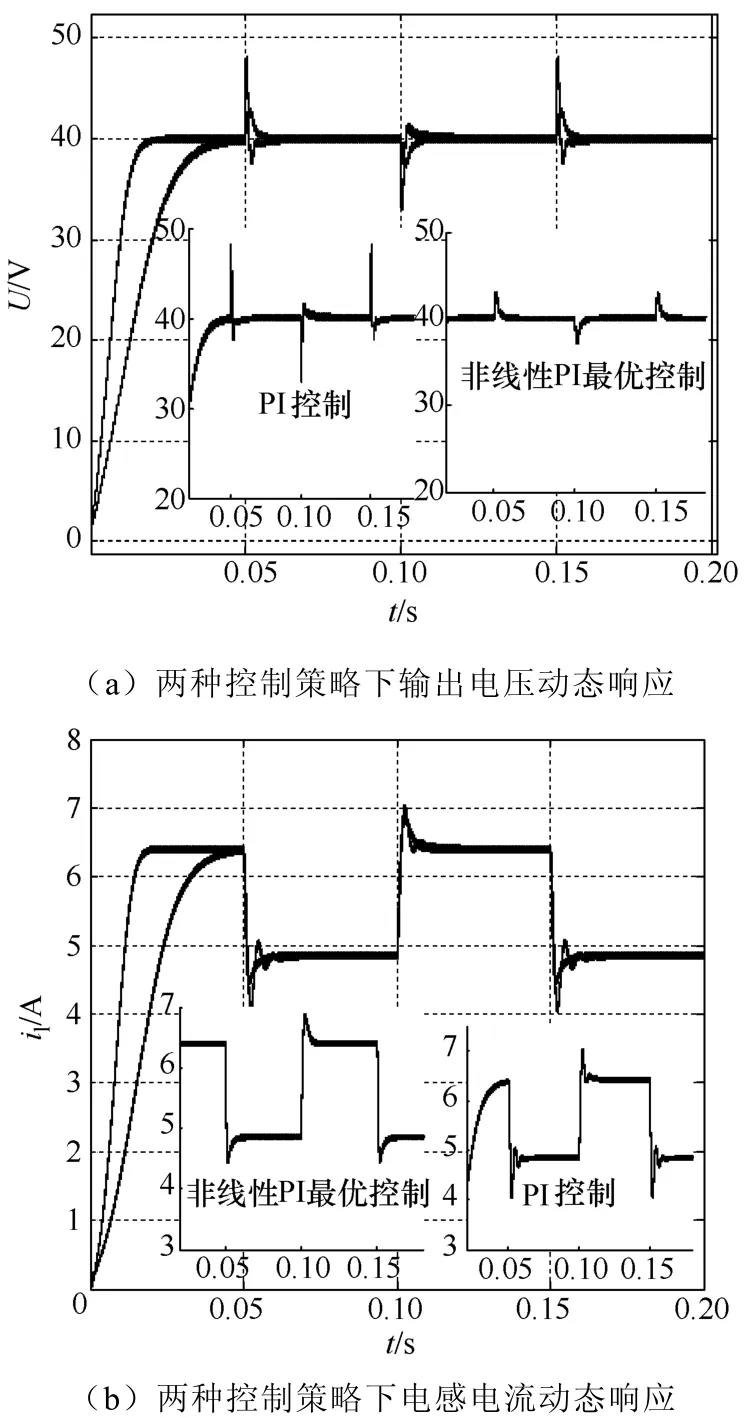
图5负载扰动下的动态特性
3.5 输入电压扰动下动态响应
图6 为输入电压由30V跳变到35V时两种控制策略的动态响应曲线。其中图6(a)为两种控制策略下输入电压突变时,输出电压的动态响应对比曲线图。图6(b)为两种控制策略下输入电压突变时,电感电流动态响应对比曲线图。由图6可知,在非线性PI控制策略下,输入电压扰动时电感电流和输出电压有些许的超调,但很小且很快恢复到稳定值。而在PI控制策略下,在输入电压突变时电感电流和输出电压都存在超调和振荡,并且需要一定的时间恢复到稳定值,超调量大。因此,采用非线性PI最优控制略,系统对输入电压扰动有更好的鲁棒性。
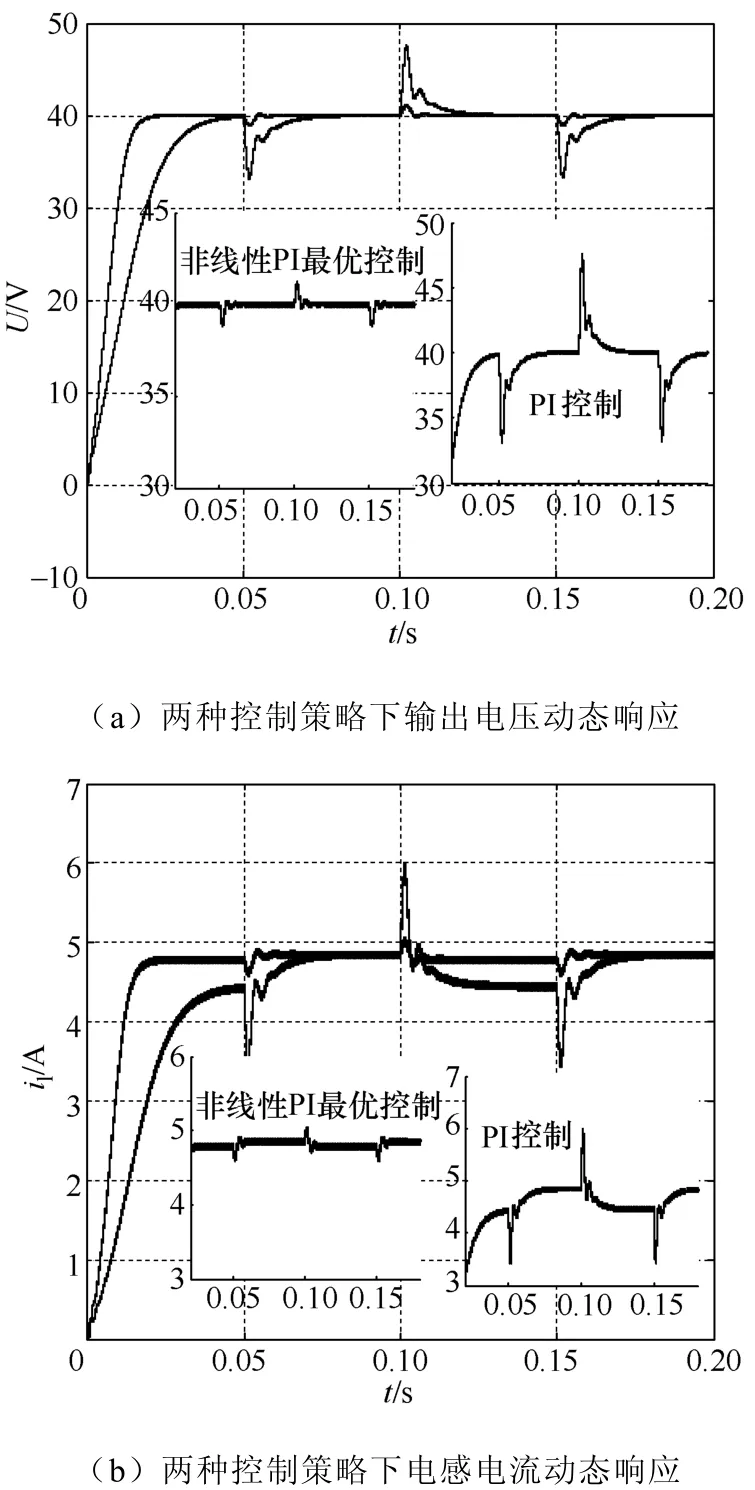
图6 输入电压扰动下的动态特性
3.6 电感值扰动下的鲁棒性
为进一步验证所提控制方法对系统参数改变所表现出来强鲁棒性,选取多组输入电感值L=2mH,5mH、10mH。在保持控制系统不变的前提下,当比较电感值逐渐增大时,Buck-Boost变换器系统的起动过程如下。
图7为电感L=2mH、5mH、10mH时,变换器的起动波形。由图7可得,虽电感值不断增加,但起动速度几乎不变;电感L=5mH时虽有些许超调但很快达到稳定;当电感L=10mH时,起动出现很大振荡,但趋于稳定,且最终在0.18s时达到稳定值。参数扰动仿真实验进一步验证了所提策略具有强鲁棒性和良好的起动特性。
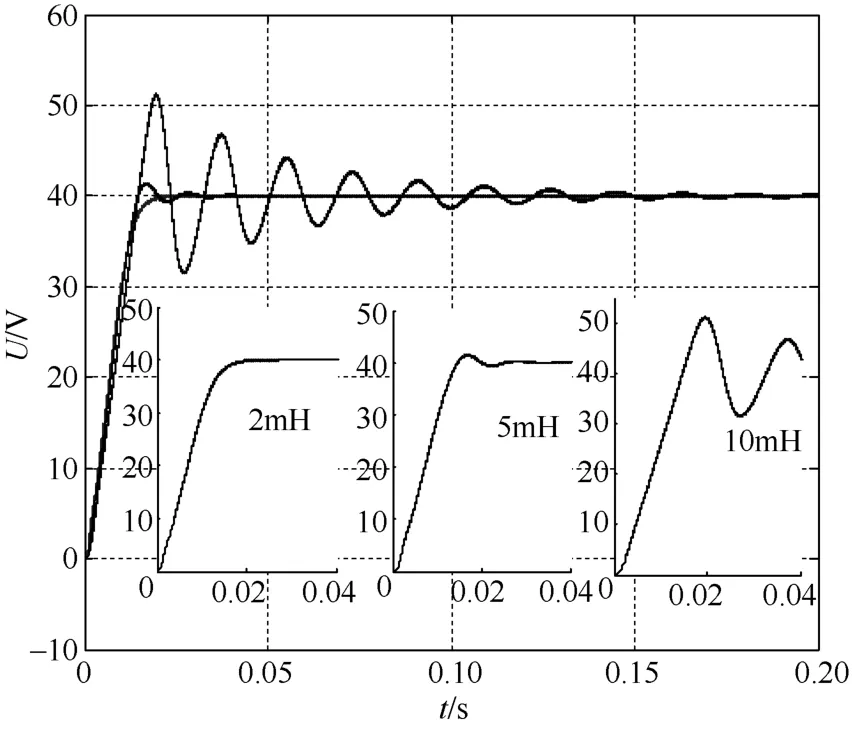
图7 不同电感值下的起动波形
4 结论
研究非线性控制技术可从根本上解决传统线性控制技术用于开关变换器的缺陷。为此,本文采用状态反馈精确线性化最优控制与传统的PI控制相结合的控制方式及非线性PI最优控制,对开关变换器进行控制。通过仿真实验研究,验证了本文所采用的控制方法正确性与可行性,得出所用策略具有以下优点:
1)采用非线性 PI最优控制能有效的改善电力电子变换器模型的控制特性。利用精确反馈线性化,实现了原非线性系统的解耦控制,使系统的动态响应速度提高,稳态精度得到改善。
2)系统具有良好的响应特性与稳态特性,并且系统对负载、输入电压在一定范围内变化时具有很强的鲁棒型。
[1] 乐江源, 谢运祥, 洪庆祖, 等. Boost变换器精确反馈线性化滑模变结构控制[J]. 中国电机工程学报,2011, 31(30): 16-23.
[2] 乐江源, 谢运祥, 冀玉丕, 等. CCM Buck变换器的精确反馈线性化滑模变结构控制[J]. 华南理工大学学报(自然科学版), 2012, 40(2): 130-135, 160.
[3] 帅定新, 谢运祥, 王晓刚. Boost变换器状态反馈的精确线性化控制[J]. 华南理工大学学报(自然科学版), 2009, 37(2): 134-139.
[4] 邓卫华, 张波, 胡宗波, 等. CCM Buck变换器的状态反馈精确线性化的非线性解耦控制研究[J]. 中国电机工程学报, 2004, 24(5): 120-125.
[5] 张国荣, 武志强, 马催. Buck-Boost基于精确反馈线性化统一控制研究[J]. 电力电子技术, 2016, 50(7): 4-7.
[6] 邓卫华, 张波, 丘东元, 等. 电流连续型 Boost变换器状态反馈精确线性化与非线性 PID控制研究[J].中国电机工程学报, 2004, 24(8): 45-50.
[7] 乐江源. 基于微分几何理论电力电子变换器非线性复合控制研究[D]. 广州: 华南理工大学, 2011.
[8] 吴忠, 刘朝辉. 基于电流模式的 DC/DC升压变换器非线性PI控制[J]. 中国电机工程学报, 2011, 31(33):31-36.
[9] 孙大鹰, 徐申, 孙伟锋, 等. Buck型 DC-DC变换器中数字预测模糊 PID控制器的设计与实现[J]. 东南大学学报(自然科学版), 2014, 44(5): 897-901.
