改进生物地理学优化算法在配电网无功优化中的应用

2018-03-30,

上海电力大学学报 2018年1期

(1.上海电力学院, 上海 200090; 2.国网浙江省义乌市供电公司, 浙江义乌 322000)

配电网无功优化主要解决以下两个问题:一是确定无功补偿点;二是确定无功补偿容量.其中存在的问题是解的维数高,以及系统的非线性和复杂性.为了解决这类问题,一般有两种思路:一是数值计算法,二是人工智能算法.数值计算方法包括简化梯度法[1]、牛顿法[2]、二次规划法[3]、逐次线性规划法[4]、混合规划法[5]和内点算法[6]等.

近年来,人工智能算法迅速发展,解决上述问题的能力也越来越受到重视.很多国内外学者在这方面做了大量研究.张庭场等人[7]将改进粒子群算法应用于配电网的无功优化,在确定无功补偿点和补偿容量方面有很好的效果;文献[8]将云自适应梯度改进的粒子群算法应用于电力系统的无功优化,与其他算法的无功优化结果相比,能获得更小的网损;文献[9]将差分法和生物地理学结合应用在潮流优化上也取得了很好的优化效果.

生物地理学优化算法(Biogeography-Based Optimization,BBO)[10]是受到物种迁徙过程的启发而产生的一种智能算法.该算法是将各个栖息地看成孤岛,通过生物种群在各个孤岛之间的迁徙和变异来交换信息,不断进行进化,以实现算法寻优.但由于其搜素能力不强,在算法后期各孤岛信息交换分享的完成使彼此趋于相同,很容易陷入局部最优而无法寻找真正的最优值.为解决这一问题,本文在变异操作中引入遗传算法,通过遗传算法的内部变异能力提高其搜索能力,进而增加种群的多样性.改进后的算法兼顾了全局搜索能力和信息利用能力,将改进后的算法应用于配电网的无功优化,取得了很好的优化效果.

1 配电网无功优化的数学模型

1.1 目标函数

配电网无功优化主要是通过选择合适的节点安装无功容量合适的电容器,使各个静态时段内降损收益总和最大,以提高电能质量.鉴于此,本文目标函数为同一时间段内配电网优化前后的电量损差值,即网损差值.其数学描述为:

(1)

式中:Pm——某时段内补偿后的损耗电量;

Pm0——该时段内补偿前的初始损耗电量.

电能损耗一般包括上游输电线路的损耗和变压器损耗电量,损耗值可用各节点相关数据,经由潮流计算得出.考虑算法寻优的最终需求,适宜度函数J取为:

(2)

1.2 约束条件

1.2.1 等式约束条件

等式约束即为潮流约束,一般包括了各节点的有功和无功平衡约束.其定义为:

(3)

式中:PGj,PLj——节点j处发电机有功出力和负荷有功功率;

M——电网节点总数;

QGj,QLj,QCj——节点j处发电机注入的无功功率、负荷无功功率和容性无功补偿装置容量.

1.2.2 不等式约束条件

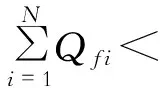
2 无功优化的分区

由于优化前无功补偿点是不确定的,因此先采用最大-最小电气距离法[11]来进行分区.这样可以保证补偿点确定的科学性,也更能满足无功就地补偿的需求,不至于欠补偿或者过补偿.

(4)

由式(4)可知:无功功率与电压是强耦合关系,而有功功率与电压是弱耦合关系.本文选择固定的节点有功功率注入量,即ΔPi=0,主要考虑无功功率与电压的关系.

由于补偿点没有确定,故先不计算电容补偿容量.通过计算无功功率变化量ΔQi对电压变化量ΔUi的影响,即通过求ΔQi对ΔUi的偏导数来计算二者的相关性,得到相关性矩阵;再利用相关性矩阵计算相对应的电气距离,计算流程如下:

(5)

式中:J——无功变化量对电压变化量的灵敏度;

A——距离相关性矩阵;

Dij——节点i和节点j间的最大电气距离.

分区所用的基本方法是最大-最小电气距离法,具体的分区步骤是:首先,以电源点为第1分

区基准点Z1,计算剩余节点的相关性得到A,利用A计算出距离Z1的各节点的最大电气距离,将最大电气距离最大的Di1所对应的节点i作为第2分区基准点Z2;然后,以Z2为基准点,再次计算与其相连接的孤点的最大电气距离,选择与Z2间最大电气距离最大的点作为第3分区基准点Z3;最后,以这些基准点为中心分区,将与基准点的最大电气距离最小的点合并在该基准点所在区域,如此循环往复.

按以上方法将IEEE 34节点系统分区并重新编号,如图1所示.由图1可以看出,将IEEE 34节点系统分为3个区,可得第1分区的节点为(1,2,3,4,12,13,14,15).将其重新排序,得到新的序列为(1,2,3,4,5,6,7,8).节点1～8为第1分区;节点9～22为第2 分区;节点23～33为第3分区.

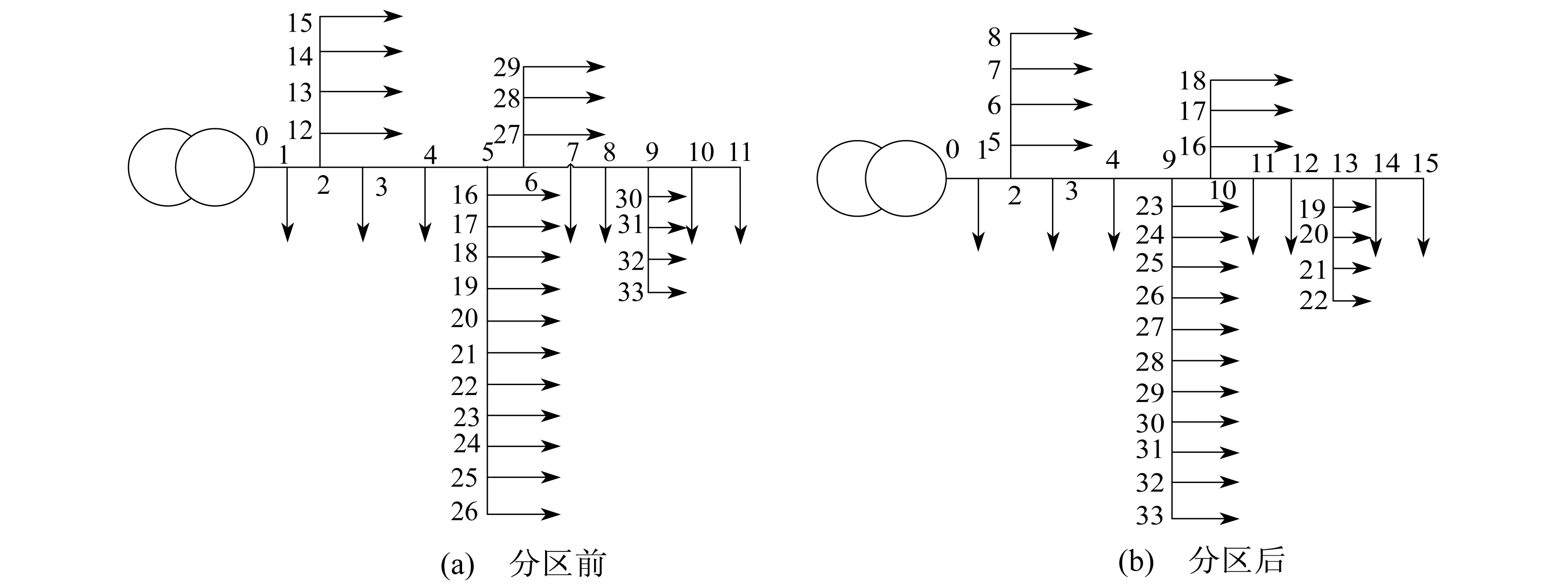
图1 IEEE 34节点系统模型

3 改进生物地理学算法

3.1 生物地理学算法简介

生物地理学算法[10]的主要理论是:某一个孤岛是否适合生物种群居住主要依赖于其适宜度指数(Habitat Suitability Index,HSI).HSI越高越适合种群生存,HSI低则不适合种群生存.某孤岛HIS高,物种数量多,竞争就会加剧,进而迁入率就会降低,迁出率相应会增加;反之,迁入率会增加,迁出率会相应变低.若某孤岛的HIS一直处于较低水平,则极有可能因为发生天灾而造成该孤岛物种灭绝或者产生突变.

3.1.1 迁移

在BBO算法中[12-14],适宜度值是表示孤岛是否适宜种群生存的一个参数,适宜度值越高的孤岛越适合种群生存.在BBO算法流程中,高HIS值的解和低HSI值的解之间有一个信息交互的机制,该机制一般称为迁移操作.图2给出了某个孤岛的余弦迁移模型.

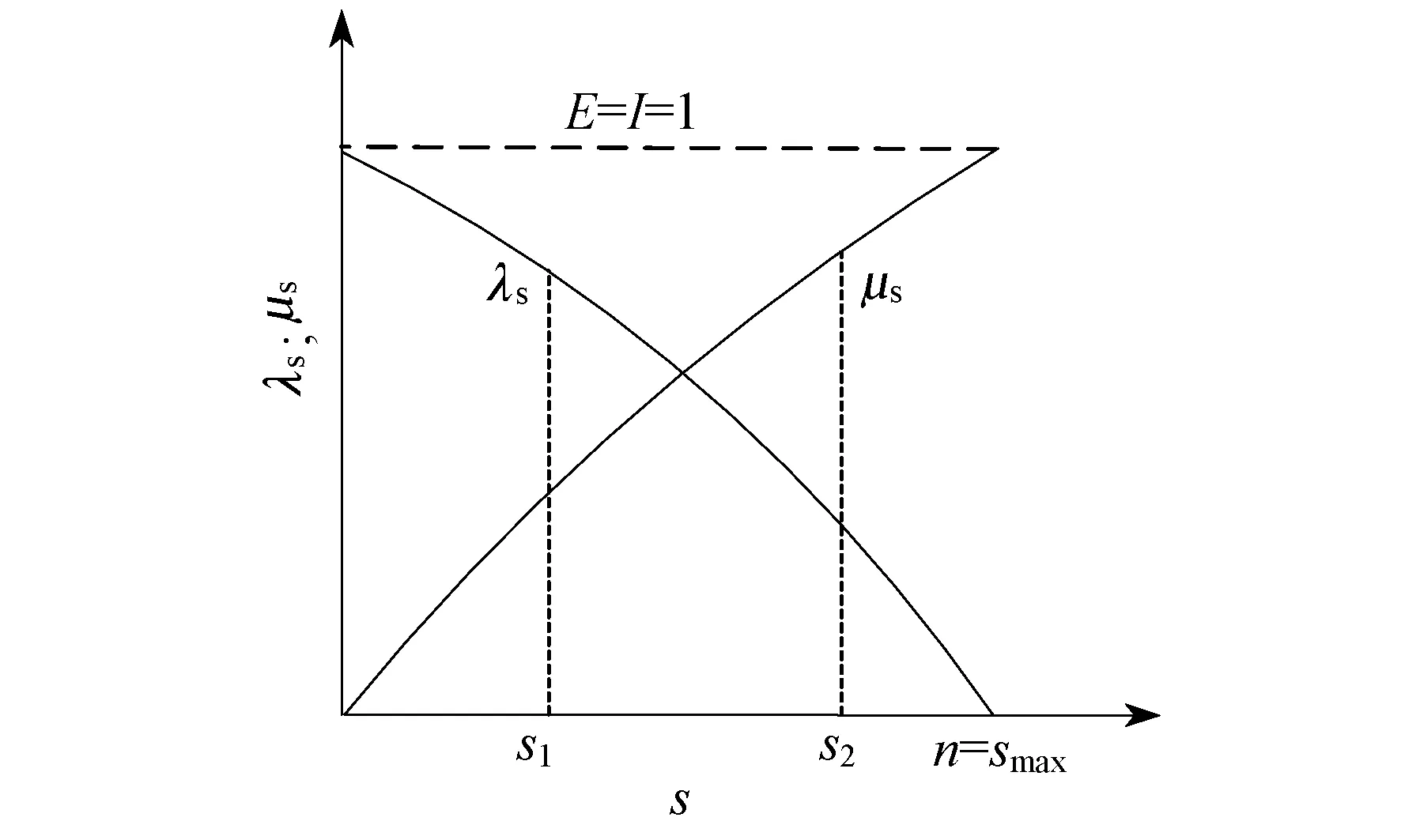
图2 BBO算法迁移模型

余弦迁移规律为:

(6)

式中:λs——种群数量为s时孤岛的迁入率;

s——当前种群数量;

n——最大种群数量;

I——最大迁入率;

μs——种群数量为s时孤岛的迁出率;

E——最大迁出率.

在该算法中,设置E=I=1.

3.1.2 变异

鉴于迁移机制的特点,迁移过程无法产生新的变量,则使得种群缺乏多样性.为了增加种群的多样性,BBO算法引入了一个变异算子.变异算子的大小由各个孤岛的物种数量概率决定,两者之间成反比的关系,即孤岛物种数量概率越高变异率越低.同时,为避免变异破坏高HSI的解,可以保留部分精英个体,使得这些较好的孤岛特征得到保护[14].

另外,BBO突变机制具有问题依赖性,可根据问题的不同进行相应调整.由于基本BBO算法仅采用随机变异,搜索后期缺乏搜索能力,因此利用遗传算法强大的开发搜索空间能力,提出了一种改进的BBO算法[12-14].

3.2 利用遗传算法改进的BBO算法

3.2.1 遗传算法改进BBO算法原理

BBO算法通过迁移操作进行信息共享,通过变异操作增加种群多样性和搜索的深度.由于变异算子为随机变异,而且每次只变异一个特征向量,变异效果较差,搜索能力差.因此,本文结合遗传算法来改进BBO算法,改进后的生物地理学遗传算法(Biogeography-Based Optimization Geneic Algorithm,BBOGA)流程如图3所示.

3.2.2 与其他改进算法的比较

相较于差分BBO算法、混沌BBO算法等改进算法,本文提出的改进算法更多地考虑BBO算法的基本原理是取自生物的迁徙行为,而遗传算法研究的也是生物内部进化的原理.差分BBO算法和混沌BBO算法都是直接对变异操作进行改进,虽然能够提高算法的开采能力,但也会造成过度开采,这样不仅破坏了算法的整体性能,而且也会加大算法的复杂性.本文提出的改进算法由于只选择对一半的对象使用改进算法替代变异操作,有效地避免了算法的过度开采,同时降低了算法的复杂性,大大提升了收敛速度和能力.

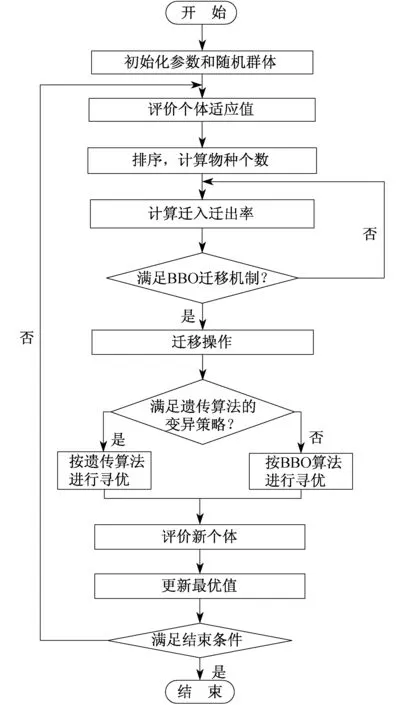
图3 BBOGA算法流程示意

3.3 测试函数的测试结果

为了验证改进后算法的性能[15],利用几个典型标准测试函数,分别对BBOGA算法、GA算法、基本BBO算法、基本PSO算法进行测试,然后比较测试结果.

为了确保测试的准确性和公平性,算法涉及的相同参数均设置为相等,分别为:群体大小N=50,最大迭代次数maxt=100,维数D=20;BBO算法、GA算法和BBOGA算法中,I=E=1.0,最大变异概率Mmap=0.01;PSO 算法中,w=0.3,c1=c2=cj=1.实验操作系统为WINDOWS7,COREI5CPU(2.60 GHz),内存为4 GB,算法运行平台为MATLAB R2011a.每个算法分别独立运行测试函数150次,关于测试函数Quartic函数的寻优结果如图4所示.

由图4可以看出,与经典的PSO算法、BBO算法和GA算法相比,BBOGA算法的收敛精度有了显著提高.其中,基本BBO算法的收敛速度是最快的,BBOGA算法由于增加了搜索流程牺牲了一定的速度,但总体上来说收敛速度还是满足要求的.

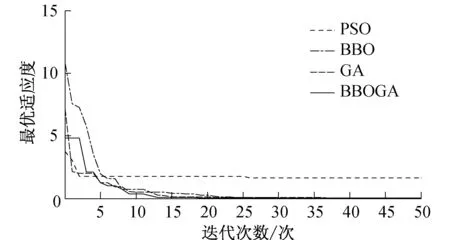
图4 测试函数结果

4 算例分析

第i个孤岛的适宜度向量[7]为xi=[xi1,xi2,xi3,xi4,xi5,xi6],其中,xi1,xi2,xi3为补偿节点编号,xi4,xi5,xi6为各补偿节点对应的无功补偿容量;按上文中所得的分区结果,各补偿点在所分区域内部进行选择,故可以设置xi1∈[1,8],xi2∈[9,22],xi3∈[23,33].根据SD 325—1989《电力系统电压和无功电力技术导则》,选择以各分区总无功负荷的1.2倍左右作为无功补偿量的上限[7],补偿量搜索步长选择10 kW(无功出力),则可以设置xi4∈[0,69],xi5∈[0,96],xi6∈[0,182].

生物地理学改进算法各参数设置如下:群体大小N=100,维数D=6,最大迭代次数maxt=100;最大迁出率和迁入率为I=E=1.0,最大变异概率Mmap=0.01;遗传算法中,交叉概率为1.0,变异概率为0.01.无功优化各参数设置如下:电压标幺值U∈[0.9,1.1],基准电压UB=12.66 kV,基准功率SB=100 MW.由于节点0为平衡节点,故其电压标幺值为1.

改进的BBOGA算法、BBO算法、GA算法均运行100次,所得结果如表1所示.BBOGA算法的最优适宜度迭代曲线如图5所示.

由表1可以看出,与其他几种优化算法相比,BBOGA算法优化后的网损最低,线损率也最低;在补偿点的选择上,3种算法都能在3个分区内寻到比较合适的补偿点,但BBOGA算法的补偿点和补偿容量最为合适.

由图5可以看出,BBOGA算法较好地克服了标准BBO算法后期搜索能力不强的问题,很好地利用了遗传算法的搜索能力,具有较好的全局搜索能力和收敛性能.

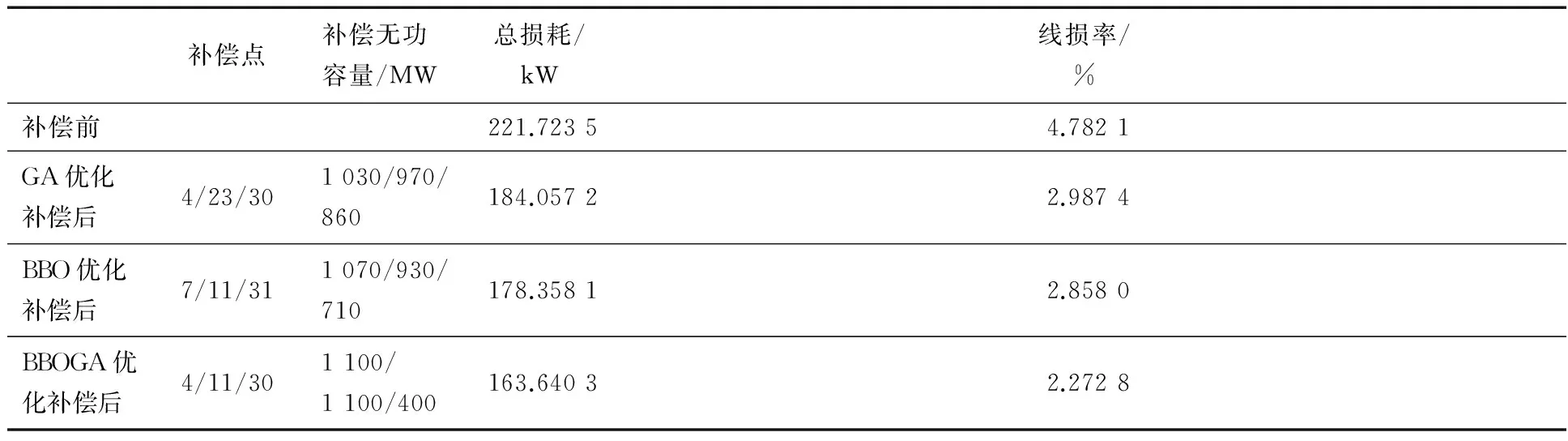
表1 不同算法无功优化后结果

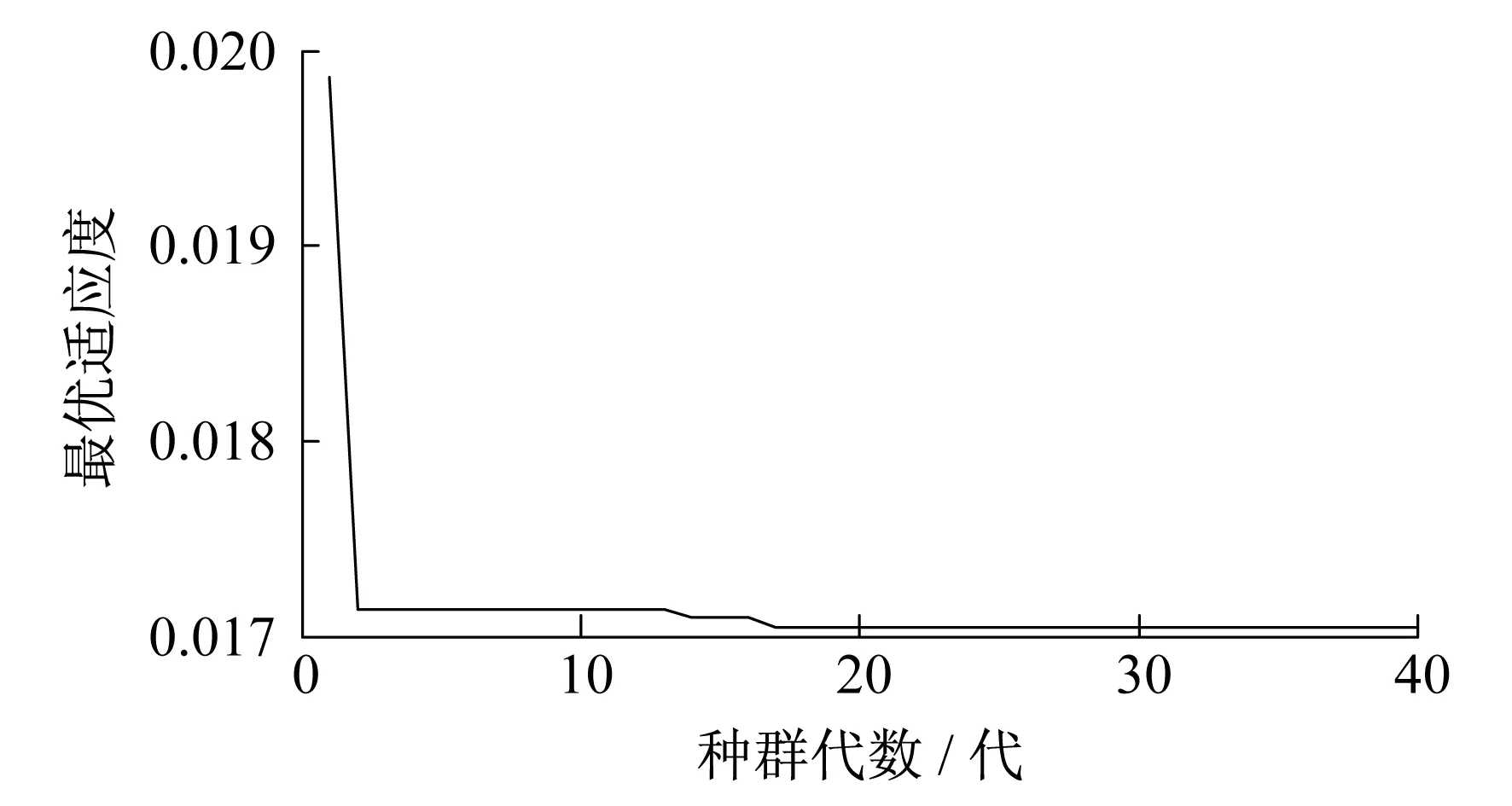
图5 最优适宜度迭代曲线

5 结语

本文采用无功分区补偿的方法有效地减少了无功补偿范围的交叉,从而缩小了补偿点搜索范围和无功补偿量搜索空间.BBOGA算法是BBO算法的一种新思路,可以有效克服BBO算法后期搜索能力不足的缺点,具有较好的全局收敛能力和搜索精度.算例仿真表明,BBOGA算法得到较优解,能够有效降低网损,因此在电力系统其他领域具有较好的工程应用前景.

[1] 刘学东,王磊,余耀.最优潮流改进梯度法的研究及应用[J].山东电力技术,2003(1):19-22.

[2] 胡泽春,严正.带最优乘子牛顿法在交直流系统潮流计算中的应用[J].电力系统自动化,2009,33(9):26-31.

[3] 毕兆东,王建全,韩祯祥.逐步二次规划法在约束潮流中的运用[J].电网技术,2003,27(2):30-33.

[4] 邓佑满,张伯明,相年德.配电网电容器实时优化投切的逐次线性整数规划法[J].中国电机工程学报,1995,15(6):20-28.

[5] 许丹,夏少连,丁强,等.基于启发式混合整数规划法求解大规模机组组合问题[J].电力系统保护与控制,2012,40(21):1-6.

[6] 张锋,段余平,邱军,等.基于粒子群算法与内点算法的无功优化研究[J].电力系统保护与控制,2010,38(13):11-16.

[7] 张庭场,耿光飞.基于改进粒子群算法的中压配电网无功优化[J].电网技术,2012,36(2):158-162.

[8] 祝洪博,徐刚刚,海冉冉,等.基于云自适应梯度粒子群算法的无功优化[J].电网技术,2012,36(3):162-167.

[9] 李静文,赵晋泉,张勇.基于改进差分进化-生物地理学优化算法的最优潮流问题[J].电网技术,2012,36(9):115-119.

[10] SIMON D.Biogeography-based optimization[J].IEEE Transactionson Evolutionary Computation (S1089-778X),2008,12(6):702-713.

[11] 李磊,黄彦全,董家读,等.基于无功/电压控制的电网优化分区方法[J].电力系统保护与控制,2010,14(3):88-92.

[12] WANG C R,WAN N N,DUAN X D,etal.Survey of biogeography based optimization[J].Computer Science,2010(7):34-38.