基于先进控制算法的CFBB床温控制系统研究
2018-03-30张保生
杨 宣,张保生
(中国矿业大学 电气与动力工程学院,徐州 221116)
床层温度是CFBB的一项重要指标,它对炉膛的安全运行和炉内的各种化学反应速率有所影响。它还直接关系到锅炉的设备安全、燃烧率和污染物的排放量。CFBB的床层温度通常情况下保持在850℃左右,其参数的过高或者过低对于CFBB的安全运行以及经济性都是有所影响的。要是温度太高,就会导致炉内脱硫的效率降低,污染物的排放量也会相应增加,甚至会出现CFBB循环流化燃烧失败、毁坏风帽、以至于燃料结焦直至停机停炉;要是温度太低,就会出现传热系数变低,炉膛内出现不稳定燃烧,锅炉的效率变低,脱硫的效果变差,污染物的排放量也会相应增加,甚至会出现大规模未燃烧颗粒汇集在尾部烟道导致爆燃的现象。
正是由于CFBB床温的高低既影响炉内熄火与否和结焦(即安全经济性),又决定炉内氮氧化物的排放量和脱硫效果(即环境效果),所以CFBB的床温是锅炉运行中最重要的指标之一,国内的CFBB尽管通常都安装了基于PID的床温闭环控制回路,然而在实际的运行过程中,基于PID的回路在投入自动时难达到很好的效果。尤其是在出现较大的负荷波动时,其自动投入效果更差。何况对于CFBB这种多变量耦合、大时滞、非线性、大惯性的燃烧控制系统,基于PID控制的床温控制已经很难达到很好的效果,所以对CFBB床温控制进行先进控制算法的研究,设计出具有较高可靠性和稳定性的床温控制系统十分必要,这也是维持正常的CFBB床温经济运行、稳定的关键。
基于以上原因,本文借助Matlab强大的数值计算能力,综合先进控制算法,力求探索适用于CFB锅炉特点、控制器适应性强、有利于提高其热工控制能力的先进控制策略。
1 几种先进控制算法的控制器
1.1 模糊-PID参数自整定系统的基本结构
模糊-PID参数自整定控制器如图1所示,是由可修正参数的PID控制器和模糊控制器FLC构成。 FLC对系统的误差值和误差变化率值进行分析,通过模糊控制规则表映射出输出模糊控制量,再通过精确化处理,输出实际值,即对PID 3个参数进行实时修正改变,补偿PID原有系数。该控制器的数学表达式为[1]
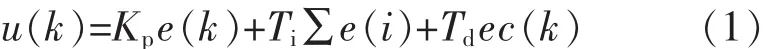
式中:e(k)为系统误差;ec(k)为系统误差变化率。
本文确定e、ec的实际误差为,在Matlab/Simulink上建立PID控制的模型,对PID的整定通过临界比例带法、衰减曲线法等得到初值,然后带入PID控制器采样PID控制入口的值及偏差值,即误差值和误差变化率值。

图1 模糊PID参数自整定控制器原理Fig.1 Principle system diagram of fuzzy PID parameter self tuning controller
1.2 双曲余弦PID控制原理
由文献[2]可知,使用误差e组成的非线性函数与常规PID控制器级联起来,就可以组成一种新的控制器,这种控制器是非线性PID控制中最简便的一种形式。如图2所示,通过对常规PID进行补偿,可以更大限度地发挥PID控制的优势,知道由误差e构成的相关函数特别多,在这里文献中选用了一种基于双曲余弦函数的非线性函数,它的结构形式如下所示:


图2 双曲余弦PID控制原理Fig.2 Schematic diagram of hyperbolic cosine PID control
在以上公式中,可以知道双曲余弦函数的值域为[1,+∞]。假如不对该非线性函数施加任何约束,当误差改变较大时,就会出现非线性补偿引起系统比例增益过大以至于整个控制系统出现振荡的情况。所以,可以通过上述函数来限制k(e)的值。
1.3 变参数PID控制原理
文献[3]分析了经典PID控制的基本原理,提出了一类非线性的PID控制器,这是一种通过根据控制偏差的大小,根据非线性函数来在线调整PID 3个控制参数的大小,以达到良好的控制要求。这是一种变参数的PID控制器。该文献提出的变系数PID控制器将kp、ki、kd取为偏差e的函数,通过偏差e的大小,不断变化这3个系数,来保障控制性能。如图3所示是该变参数结构形式的其中之一。
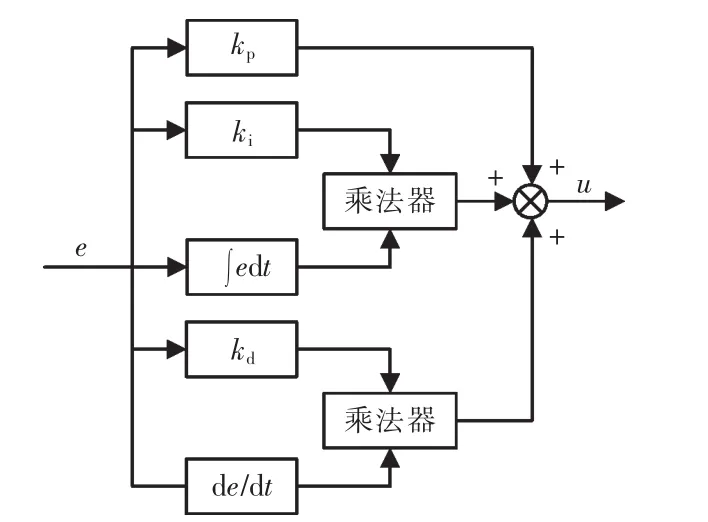
图3 变参数PID控制器原理Fig.3 Variable parameter PID controller schematic diagram
变参数的 kp、ki、kd函数如下所示:

式中:kp0、ki0、kd0为对比 PID 的参数;kp′,ki′,kI″,kd′为修正系数,由文献可知,修正系数的取值范围为kp′∈(0,1),ki′∈(0,1),ki″∈(1,+∞),kd′∈(1,+∞)。
1.4 自抗扰控制方法
在文献[4]中,提出了一种自抗扰(LADRC)的整定方法,使得LADRC控制器更易于实现且具有更广泛的使用性。在假设调节时间已知情况下,只需调节一个控制参数即可完成控制器的参数整定。在对多种多样的系统仿真试验中表明,LADRC和PID一样可以应用于不同类型的系统,相比而言LADRC能够获得更好的动态性能和性能鲁棒性。该文献所用的LADRC模型如图4所示。

图4 一种LADRC控制器原理Fig.4 A schematic diagram of LADRC controller
文献中的整定方法如下:
(1)确定系统所需的调节时间 ts,ωc=10/ts。 通过ωc可计算出kp和kd值;

(2)令 ωo=4ωc,k=4。通过 ωo、k 计算出 B1,B2,B3;
(3)逐渐增大b0值,直至系统达到控制要求。
2 控制系统数值仿真
2.1 三阶系统仿真
由文献[5]可得某三阶床温模型如下:

在Matlab/Simulink环境下,构建模糊自整定PID控制器、双曲余弦PID控制器、变参数PID控制器、自抗扰LADRC控制器、常规PID控制系统,模糊自整定PID控制器为2输入3输出的模糊控制器。并利用Simulink/NCD模块对5种控制器参数进行优化。仿真试验的输出波形如图5所示。
从图5中不容易看出不同控制算法下的性能指标,经整理可得表1,可以从表1中的数据及图5的图形走向分析不同控制算法下的控制器优缺点。
从图5和表 1,可以看出,VAPID、Fuzzy-PID、LADRC等控制器的输出响应时间相对PID控制较短,Fuzzy-PID的调节时间是众控制器中最短的,它比 VAPID 低了 250 s,比 LADRC低了 300 s,比 PID低了377.7 s,比NPID低了470 s。且超调量也比较低,NPID的静态指标虽然没有其他控制器的好,但是从图中可以看出它的飞升时间非常短,是所有控制器中输出响应动作最快的控制器,说明NPID的快速好,且超调量也比PID的好,满足工业控制的要求。至于Fuzzy-PID可以看出它的调节时间较短,超调量也比PID较短。LADRC的超调量是所有控制器中表现最优异的,没有超调量,系统的动态品质较好。
当传递函数发生变化时,即传递函数变为
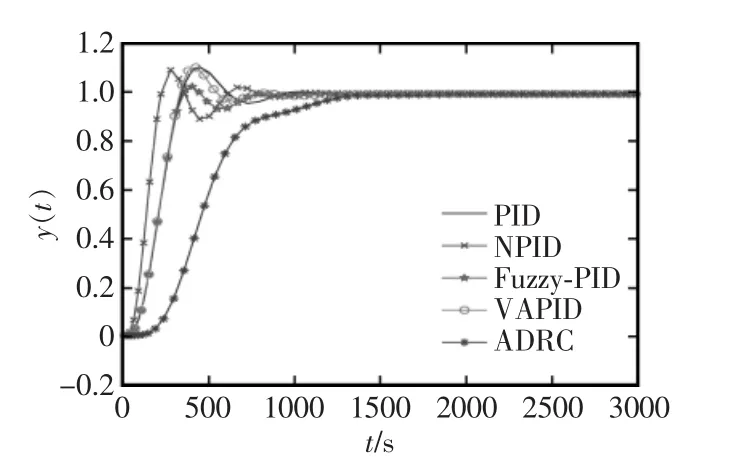
图5 不同控制器下的单位阶跃响应曲线Fig.5 Unit step response curve under different controllers
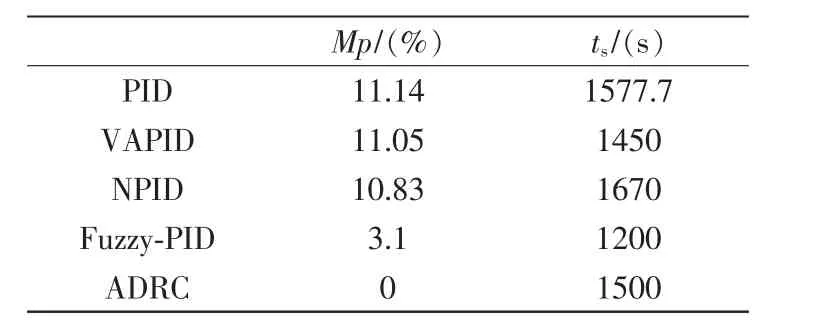
表1 不同控制器下的性能指标Tab.1 Performance indicators under different controllers

控制器的参数保持不变,其输出波形如图6所示。

图6 不同控制器下的单位阶跃响应曲线的鲁棒性能Fig.6 Robust performance of unit step response curves under different controllers
从图6中不容易看出系统的性能指标,经整理可得表2。通过分析表2和图6可得出各控制器的鲁棒性性能。

表2 传递函数变化后不同控制器下的性能指标Tab.2 Performance indexes of different controllers after the transfer function changes
从表2中,可以发现,当传递函数发生改变后,即系统的模型发生变化后,VAPID和Fuzzy-PID的调节时间是所有控制器中最短的,调节时间都达到了2500 s,但是相比之下,VAPID的超调量比PID低了0.89s,比NPID 低了 1.59s,比 Fuzzy-PID高了 12.91s,比LADRC的高了23.91s。VAPID的动态品质较PID和NPID的较好,但比Fuzzy-PID和LADRC的较差,VAPID充分改善了原有PID的性能。从图中可以看出尽管NPID的性能较其他控制器某些指标不尽人意,但是NPID仍然是众控制器中动作最迅速的,NPID控制器的飞升速度较快,NPID具有快速性的性能。LADRC控制器的调节时间较长,仅仅比PID的低了280 s。但是LADRC超调量较低,对于床温这种多变量紧密耦合的被控对象十分适用。
对该三阶对象进行抗干扰实验仿真,在2500 s时,对模糊自整定PID控制器(Fuzzy-PID)、自抗扰控制器(LADRC)、PID控制器、双曲余弦 PID控制器(NPID)、变参数PID控制器(VAPID)控制对象后加入单位阶跃响应信号。系统的输出信号和性能指标如图7所示。
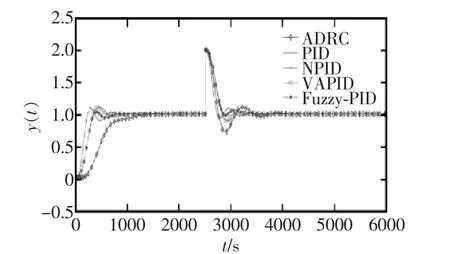
图7 加入扰动后不同控制器的输出曲线Fig.7 Output curves of different controllers after adding disturbance
从图7中,可以看到模糊PID参数自整定控制器抗干扰性不是很好,当加入扰动后,Fuzzy-PID的超调量和调节时间都较长。NPID的调节时间较少,但超调量相对较高。而VAPID和LADRC的峰值和调节时间都较低,性能指标较好。
2.2 LADRC性能研究
由文献[6],循环流化床锅炉在给煤量阶跃扰动下,床温传递函数为

对LADRC的性能曲线进行研究。分别改变b0和ωc的值,看系统的输出曲线得出结论。当b0=0.05,b0=0.06,b0=0.09,b0=0.2 时系统的响应曲线如图8所示。
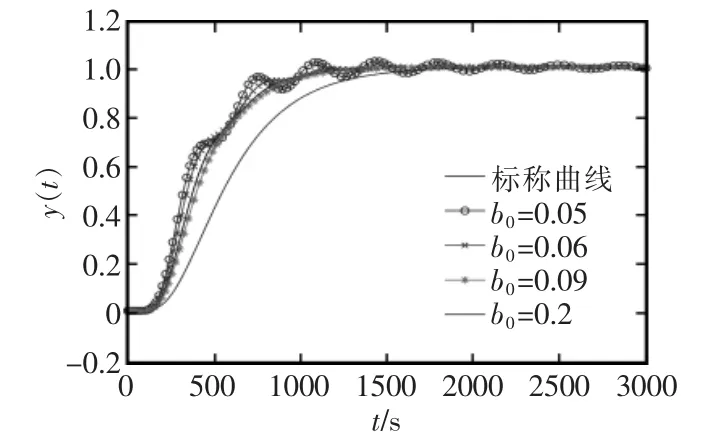
图8 b0发生变化后系统的输出响应曲线Fig.8 Output response curve of the system after the change of b0
从图8中可以看出,b0的改变对ωc的性能影响很大,当b0较小时,系统开始出现震荡,不能达到平衡。随着b0的增大系统的稳定性能上升,但是b0过大,输出曲线会出现多段小幅震荡。系统存在潜在风险。
当 ωc=0.003,ωc=0.004,ωc=0.006,ωc=0.009 时,系统的输出响应曲线如图9所示。

图9 ωc发生变化后系统的输出响应曲线Fig.9 Output response curve of the system after the change of ωc
从图9中可以看出,伴随ωc的升高,输出曲线的静态偏差逐渐减小。但是ωc过大系统会出现振荡,以至于不能平衡,但是ωc过小,会导致静态偏差过大,系统的性能指标不能满足工业控制的要求。
3 结语
在实际的运行控制过程中,不同的控制对象它们都有不同的数学结构,有些对象存在着一些延迟,有些对象比较复杂属于高阶对象,且控制的环境也大不相同,受到的扰动也不太一样,仅仅采用一种控制算法已经不能满足当前实际工业控制的需求。因此,采用不同的控制算法遴选出适合该控制模型的控制算法十分有必要,针对CFBB这种多变量耦合、大时滞、非线性、大惯性的燃烧控制系统,本文设计了4种基于先进控制算法的控制器,模糊自整定PID控制器、双曲余弦PID控制器、变参数PID控制器、自抗扰LADRC控制器。针对同一床温模型,并将这4种先进控制器与常规PID控制器进行对比。发现模糊自整定PID比常规PID控制的超调量小,调节时间比PID控制系统的短,鲁棒性实验中Fuzyy-PID的适应性较好。在Simulink环境下,使用S-Function语言实现对双曲余弦PID控制器、变参数PID控制器的参数求取,进行双曲余弦PID、变参数PID和常规PID床温控制系统的仿真研究,结果表明双曲余弦PID、变参数PID控制提升了常规PID控制的性能。基于对自抗扰控制器(LADRC)的设计和分析,获得LADRC控制器的参数整定方法,计算出不同传递函数模型下ADRC控制器的最优参数,并进行LADRC床温控制系统的闭环仿真和Monte-Carlo随机实验。分析和仿真结果一致表明,LADRC能够有效抑制超调现象,且具有较好的性能鲁棒性和抗扰性。
本文的研究结果显示了先进控制算法在热工过程控制中具有很好的应用前景。可以预料到的是,将会有越来越多的先进控制器将会运用在工业控制中。随着现代科技不断进步和人们对于控制品质要求的不断提升,各种各样的先进控制算法一定会在工程实际中得到更多应用。另外当前控制领域的国内外专家学者对于先进控制算法的研究还在不断进行,可以预料的是今后将会出现一批前所未闻的新型先进控制算法,这些控制算法将会运用在人们生活中的各个领域,将会极大地丰富我们的世界,同时这些理论也会促进其他理论的发展,对人们探寻科学世界提供了阶梯。
[1]Ydstie B.E.Extended horizon adaptive control[C]//IFAC 9th World Congress,Budapest,Hungary,1984.
[2]苏玉鑫.一种新型非线性PID控制器[J].控制与决策,2003,18(1):126-128.
[3]钟庆昌.变参数 PID 控制器[J].信息与控制,1999,28(4):273-277.
[4]陈星.自抗扰控制器参数整定方法及其在热工过程中的应用[D].北京:清华大学,2008.
[5]刘长良.基于PI-DMC算法的循环流化床床温控制系统的研究[J].热力发电,2013,42(11):122-126.
[6]林永君.基于自抗扰控制的循环流化床锅炉床温系统的研究[J].热能动力工程,2010,25(9):49-48.
