基于GA的自适应PID在直冷机组背压控制的应用

白建云 ，曲 燕 ，李永茂 ，冯 赓 ，张润元

（1.山西大学 自动化系，太原 030013；2.山西平朔煤矸石发电有限公司，朔州 036800）

在燃煤电厂运行控制中，直接空冷机组的背压是一个极其重要的参数，对背压控制的好坏直接关系到机组的安全经济运行。由于直接空冷凝汽器具有非线性、时变、多变量以及大迟延的复杂特性，使得常规PID无法达到对背压理想的控制效果[1-2]。遗传算法GA是一种基于自然选择和自然遗传的全局优化算法，具有控制思路简单、易于实现、应用效果好等优点，近年来在自适应控制、组合优化等许多方面得到了广泛应用，能够在所有的解决方案中通过搜索寻找出最符合所针对问题的解决方法。

在此，提出一种基于遗传算法的参数自适应PID控制策略，充分利用遗传算法操作方便、搜索速度快的优势，实现PID参数的在线自适应调整。

1 遗传算法对PID控制器参数的优化

1.1 遗传算法基本原理

遗传算法的出发点是一个简单的群体遗传模型。该模型基于以下假设：

（1）染色体（基因型）由一固定长度的字符串组成，其中的每一位具有有限数目的等位基因。

（2）群体由有限数目的基因型组成。

（3）每一基因型有一相应的适应度，表示该基因型生存与复制的能力。适应度为大于零的实数，适应度越大表示生存能力越强。

设字符串的长度为l，等位基因数为2，用0和1表示，则基因型为

式中：ai∈｛0，1｝，i=1，2，…，l。 群体中有 n 个基因型，用Aj表示第 j个，j=1，2，…，n。 各基因型均具有相应的大于零的适应度fi。

标准遗传算法的计算流程如图1所示。

图1 遗传算法的PID控制器参数优化流程Fig.1 Genetic algorithm PID controller parameter optimization flow chart

1.2 遗传算法的实现

1.2.1 二进制编码

二进制编码是遗传算法中最常用的一种编码方法。二进制编码符号串的长度与问题所要求的求解精度有关。假设，某一参数的取值范围是［Umin，Umax］，用长度为l的二进制编码符号串来表示该参数，则它共产生2l-1种不同的编码，若使参数编码时的对应关系为

则二进制编码的编码精度为

假设某一个体的编码为 bl，bl-1，bl-2，…，b2，b1，则对应的译码公式为

1.2.2 种群的设定

群体设定的主要问题是群体规模 （群体中包含的个体数目）的设定。作为遗传算法的控制参数之一，群体规模和交叉概率、变异概率等参数一样，直接影响遗传算法的效能。当群体规模N太小时，遗传算法的搜索空间中解的分布范围会受到限制，具体表现在得到的是局部最优解；较大的群体规模可以保持群体的多样性，但也意味着存在较高的计算成本。综合考虑，适当的群体规模为N=10～200。

1.2.3 适应度函数

对适应度函数的唯一硬性要求是，对给定的输入能够计算出可以用来比较的非负输出，以此作为选择操作的依据。一个控制器的好坏，可以通过被控对象的输出响应来评价。为获取满意的过渡过程动态特性，采用误差绝对值时间积分性能指标作为参数选择的最小目标函数；为防止控制能量过大，在目标函数中加入控制输入的平方项u2（t）。在此参数选择的最优指标为

式中：e（t）为系统误差；u（t）为控制器输出；tu为上升时间；ω1，ω2，ω3为权值。 通过调节权值 ω1和 ω3的相对大小，还可以体现对调节时间和超调量的重视程度。

当使用式（4）对控制器参数进行优化时，需采用惩罚措施去克服系统动态响应中可能产生的超调。因此，将超调量作为最优指标的一项，将式（4）改进为

式中：ω4为权值，且 ω4＞＞ω1。

控制系统参数优化问题是一个非负目标函数的最小化问题，然而遗传算法的优化方向是对应适应度增加的方向，故按

将目标函数 J（x）转换为适应度函数 f（x），即用目标函数求出最小值，利用遗传算法将适应度函数值排序取最大值。

1.2.4 遗传操作

遗传操作包括3个基本遗传算子，即选择、交叉和变异。其操作方法如下：

（1）选择算子是指从群体中选择优质个体，淘汰劣质个体。

（2）交叉算子在遗传算法中起核心作用，交叉是指对2个父代个体的部分结构进行重组而生成新个体的操作。交叉算子需保证前一代中优质个体的性能在下一代中尽可能遗传和继承。

（3）变异算子是改变群体中个体串的某些基因座上的基因值。对于由字符串｛0，1｝生成的二值码串来说，变异操作就是把基因座上的基因取反，即1→0 或 0→1。

1.3 基于遗传算法的自适应PID整定

一般来说，控制参数与性能指标之间存在着复杂的非线性关系，其精确地表达很难获得。设性能指标与控制参数之间的代数关系为

对任意 2 点（θ1，Z1），（θ2，Z2）有

式中：I为单位阵；ο（·）为高阶项。 式（5）可近似为

可通过辨识方法对A和B进行辨识，获得性能指标与参数间的近似表达，则可用遗传算法进行在线参数优化。

利用遗传算法进行控制器在线寻优的系统构成如图2所示。

利用Matlab软件编写程序包括遗传算法寻优主程序、目标函数子程序和约束条件子程序等。该寻优算法以系统误差绝对值时间积分最小为目标函数，Kp，Ki，Kd为所需寻优参数。

图2 基于GA的参数优化PID控制Fig.2 Parameter optimization PID control based on GA

—遗传算法寻优部分主程序如下：

—目标函数部分子程序如下：

2 仿真及结果分析

燃煤电厂直接空冷机组的背压设定值，随着季节、环境的改变而不断变化。直冷机组背压控制系统通过控制轴流风机的转速，提供适当量的冷却介质将凝汽器内的蒸汽冷却成凝结水来改变背压。

在此，以山西某300 MW直接空冷机组背压控制系统为例，在70%负荷下的近似数学模型为

应用Matlab的Simulink仿真工具箱搭建仿真系统，将基于GA的自适应PID控制算法与常规PID单回路控制法（采用衰减曲线法整定）进行比较。设置系统采样时间为2 s，输入信号为单位阶跃信号，种群个体（Kp，Ki，Kd）长度为 10，采用二进制编码方式。

2.1 仿真参数设置

常规PID单回路控制法采用衰减曲线法整定参数，Kp=1.61，Ki=0.105，Kd=15.35。

基于GA的自适应PID仿真参数设置见表1。

表1 遗传算法优化PID的仿真参数Tab.1 Genetic algorithm optimization PID simulation parameters

2.2 优化参数

运行程序，经过100次的迭代后，得到的优化参数见表2，Matlab运行结果如图3所示。

表2 遗传算法优化后的参数Tab.2 Genetic algorithm optimized parameters

2.3 仿真结果

在单位阶跃扰动作用下，系统性能指标J的优化过程、单位阶跃响应分别如图4和图5所示。性能指标比较结果如表3所示。

对比以上仿真结果可知，在单位阶跃扰动作用下，经过遗传算法优化的PID控制效果要明显优于常规PID控制，而且系统的超调量和调节时间都大大缩短，表现出良好的动静态性能。

图3 PID控制器参数寻优结果Fig.3 PID controller parameter optimization results

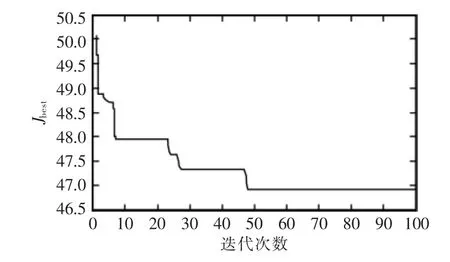
图4 性能指标J的优化过程Fig.4 Optimization of the performance index J

图5 单位阶跃扰动作用下2种控制系统响应曲线Fig.5 Response curves of two control systems underunit step disturbance

表3 性能指标比较Tab.3 Comparison of performance indicators

在机组实际运行中，受锅炉负荷、环境温度、风机转速和风速等因素的影响，直接空冷凝汽器的背压发生变化，被控对象模型参数也必然发生变化。为了分析背压控制系统的自适应性，在表3所示2种控制方式控制器参数不变的情况下，以下3种参数分别摄动进行仿真研究：

（1）被控对象增益变化，Gm（S）变为 G′m（S）=2种控制方式下单位阶跃响应曲线如图6所示。

图6 对象模型增益变化时的阶跃响应曲线Fig.6 Step response curve of the object model gain change

（2）被控对象惯性时间常数变化，Gm（S）变为种控制方式下的单位阶跃响应曲线如图7所示。

图7 对象模型时间常数变化时的阶跃响应曲线Fig.7 Step response curve of the object model time constant changes

（3）被控对象迟延时间变化，Gm（S）变为 G′m（S）=种控制方式下的单位阶跃响应曲线如图8所示。

在常规PID控制系统中，整定后的参数不能随着对象模型的变化而调整出相应工况下最优PID参数；遗传算法自适应PID控制却能在对象模型变化时，在模型辨识的基础上对PID参数进行优化，从而实现自适应控制。由模型参数摄动的仿真结果可见，系统模型参数发生变化时，常规PID控制方式超调量较大，调节时间长，振荡程度加大；遗传算法优化的PID控制方式超调较小，调节时间短，对模型变化有很强的适应能力。

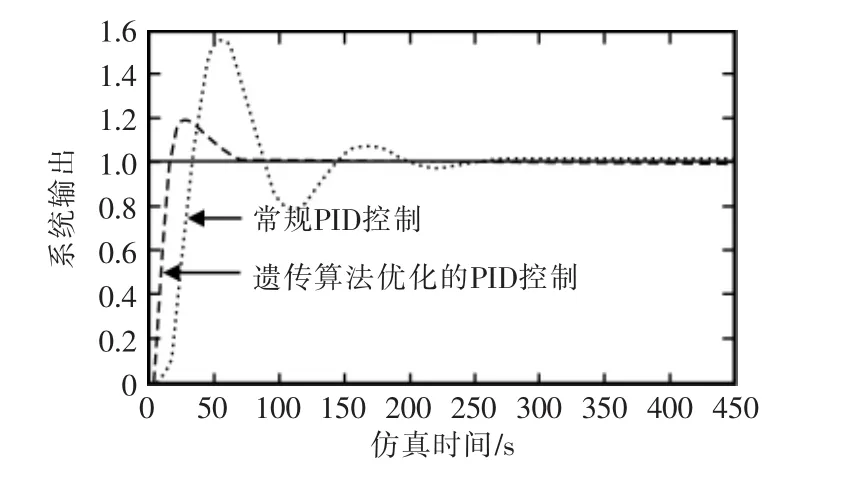
图8 对象模型迟延时间变化时的阶跃响应曲线Fig.8 Step response curve of the object model delay time change

3 结语

针对常规PID控制算法对复杂对象控制效果变差的问题，将遗传算法引入PID控制器参数优化中，对300 MW直接空冷机组背压控制系统的数学模型进行仿真。结果表明，基于遗传算法优化的PID控制器，能够使控制系统的动态性能和稳态性能得到更大程度的提高。当系统模型失配时，通过遗传算法的自学习能力，控制系统仍然能适应模型的变化，具有较强的自适应性能。该方法易于实现参数在线整定，控制效果显著，具有较高的实用参考价值，能满足直接空冷机组在不同负荷下对背压的控制要求，为背压系统自动控制策略的选择提供了一种良好可行的控制方案。

[1]王宏宇，白焰.电厂直接空冷系统汽轮机背压的控制方法[J].化工自动化及仪表，2016，43（6）：584-586.

[2]郭寻.直接空冷机组背压优化与控制方法的研究[D].北京：华北电力大学，2013.

[3]郑海霞，王林.遗传算法的自适应PID控制器的应用[J].自动化仪表，2009，30（4）：58-60.

[4]Chen Huai-zhong.Research of adaptive PID controller based on genetic algorithm[J].Applied Mechanics and Materials，2011，1151（48）.

[5]刘芳，马玉磊，周慧娟.基于种群多样性的自适应遗传算法优化仿真[J].计算机仿真，2017，34（4）：250-255.