短波突发FSK信号解调技术研究
2018-03-29崔玉娇许勇
崔玉娇,许勇
(69023部队新疆乌鲁木齐830017)
移频键控(FSK)信号作为数字通信中常见的通信方式,广泛应用于短波等中低速数据通信。由于短波通信通过电离层反射通信,其通信质量受电离层变化和噪声影响较大,且短波通信中多采用突发FSK通信,使得商用FSK解调芯片难以满足处理要求。随着软件无线电在数字信号处理领域的广泛应用[1],其高效、灵活的特点更适合于短波FSK信号解调。因此,研究基于软件无线电的FSK信号检测及解调具有重要意义[2]。
传统的FSK解调方法主要分为相干解调和非相干解调两种[3],相干解调需对频率和相位信息的精确跟踪,所需设备较为复杂;非相干解调无需相干信息而广泛使用。目前在软件无线电中最成熟的解调方法主要包括正交自延时和基于DSTFT的解调方法,基于DSTFT的解调方法更符合FSK信号特征而广泛使用[4]。文献[5]通过比较FSK信号两个载频最大峰值比的方法实现码元同步和解调,但未考虑噪声影响,无法应用于实际系统。文献[6]通过求两个载频附近最大峰值的解调方法,避免了频偏的影响,但码元同步采用粗同步,解调精度不高。徐艺文等[7]采用自适应门限方法解调FSK信号,需在不同条件下设置不同参数,系统较为复杂且未考虑突发信号的提取。
基于此,文中提出了一种基于谱熵检测结合DSTFT的突发FSK信号检测方法。该方法采用谱熵分析有效提取FSK信号,通过寻找载频附近功率谱幅值的累积量进行码元判决,提高了解调的抗噪声性能。并针对实际短波通信中载波偏移难以采用传统固定载频解调的问题,采用基于最大峰值比判决的码元同步方法,避免了噪声误判和频偏造成的同步误差,提高了系统的解调性能。
1 基于谱熵的突发信号检测
1.1 突发信号检测
实际通信中存在大量短突发和非连续信号,如何检测突发并提取有用信息对信号的解调分析及后续工作具有重要意义[8]。在实际工程中每次处理信号的长度有限,无法保证待处理数据包含信号,所以在突发信号检测前需要对信号的存在性进行判决。突发信号的常用检测方法主要分为时域法和频域法[9]。时域法主要包括自相关法,信号过零率检测和高阶累积量滑动窗口检测等,其原理是通过时域统计量区分噪声和信号,但此方法对噪声敏感,不适用与信噪比较低的突发信号检测;频域法检测主要以循环谱和幅度谱为判决量进行检测,通过噪声能量和信号能量的不同进行区分,但单纯的能量判决不适用于突发间隔较小、信噪比较低的信号,且需要已知信号的信噪比信息[10]。
1.2 谱熵分析
信息熵描述的是事件的不确定性,代表某一事件发生时所包含的信息量的数学期望,即信源的平均信息量[11]。当事件的不确定性越高时熵越大,反映了事件发生越无序。
定义事件X={x1,x2,...,xn},其分别出现的概率为p(x1),p(x2),...,p(xn),则给出离散型随机事件的信息熵为:
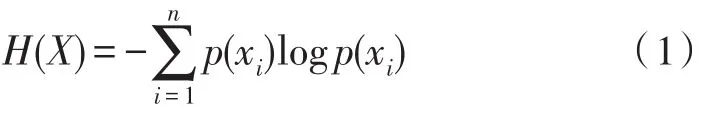
研究发现,通信信号在频域中分布在一定频带内,并且具有较强的规律性,而伴随的噪声信号在频域中分布广泛并且表现出无规律性的分布[12]。因此,通过信息熵可以有效区分信号和噪声,通过功率谱的熵可以反映完全噪声和带噪信号部分的有序性差异,实现信号段的准确检测[13]。
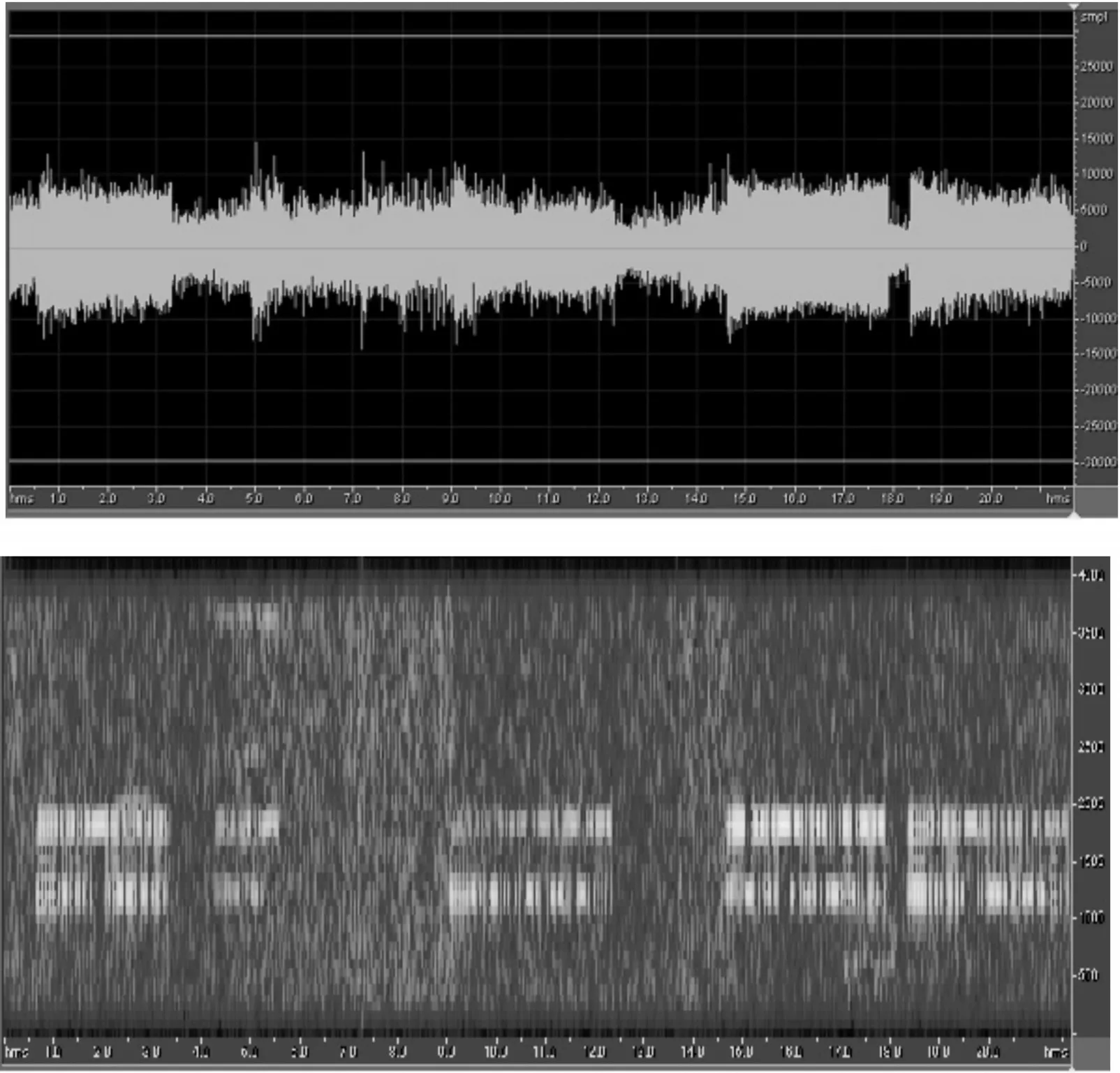
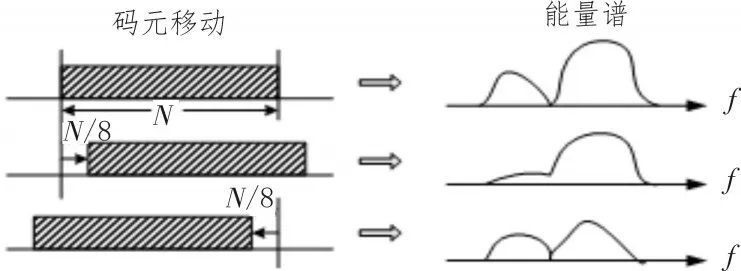
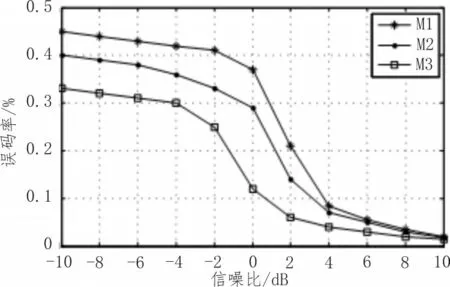
设输入信号为X={x1,x2,...,xn},1 由公式(1)可得第j帧的功率谱熵为: 短时傅里叶变换的定义为: 其中x(n)为输入信号序列,w(n)为所选窗函数,窗宽度为N。 由式(4)可知,DSTFT作为加窗的DFT变换,其将输入信号变换到离散的时频域上(nT,kF(T>0,F>0)),能够反映某一时间周期附近的频率分布情况。 典型2FSK信号的离散形式可表示为: 其中:ai代表第i个码元,N为码元宽度,fs为采样速率,f1和f2代表信号的两个载频。 由式(5)可以发现,DSTFT非常适合用于解调FSK信号。传统基于DSTFT的FSK解调如图1所示。为了减少计算量,通常取时间点为nN,即两个码元连接点上的DSTFT。从频域分析,只需比较频率点K1=[Nf1/fs]取整和K2=[Nf2/fs]取整的幅度谱值得大小即可判断0或1。 图1 传统基于DSTFT的FSK解调框图 基于以上分析,式(4)变为: 如果 |X(nN,K1)|>|X(nN,K2)|,则判断为码元0,否则为码元1。 传统基于DSTFT的FSK信号解调方法存在码元同步信息提取,频偏对解调性能的影响和突发信号初始时刻判决的问题。因此,提出了基于谱熵检测突发信号和基于抗频偏特性DSTFT的FSK信号解调方法。 基于谱熵和DSTFT的突发FSK信号解调流程如图2所示,主要包括前端处理模块、DSTFT窗同步模块和解调输出模块。其中:前端处理模块包括带通滤波和谱熵检测功能,带通滤波滤除带外噪声,提高解调性能;谱熵检测完成突发FSK信号频带内噪声段和信号段的识别和噪声去除;DSTFT窗同步模块根据短时傅里叶变换的幅度值在载频1和载频2的关系完成窗移动和码元同步;解调算法实现判决和码元输出。 图2 基于谱熵和DSTFT的突发FSK解调框图 基于突发信号解调的信号检测中,常采用短时能量法[14],通过计算一段时间内的能量值来区分信号和噪声。短波信道多采用自动增益控制(AGC)使得噪声段也有较大能量,因此能量法不适用于短波信号的盲检测,并且检测和解调同时进行,影响了解调效率。基于功率谱熵的检测方法基于信号在一段时间内的功率谱熵的变化低于噪声变化的原理进行检测,如图3所示,为某FSK短波信号的时域和语谱图。 图3 突发短波FSK信号时域图和语图 在某个时间段内,信号相比较噪声其能量集中在部分频段,起伏变化较大导致频域熵较小。而噪声分布在整个频带内且分布较为平坦,导致噪声的谱熵值较大。因此,基于功率谱熵的差异可以有效区分信号和噪声段。如图4所示,为图3中FSK信号的谱熵分布图。从图中可以看出,噪声段和信号段的谱熵具有明显差异,因此通过谱熵检测可以有效提取信息,满足突发信号解调中处理的要求。 图4 FSK短波信号谱熵图 基于谱熵的信号检测步骤包括: Step1:对输入信号进行分帧,对单帧内信号进行加窗短时傅里叶变换,得到突发信号的分帧功率谱幅度|F(m,k)|2; Step2:根据公式(2)计算基于不同频率的功率谱密度概率函数p(m,ki); Step3:根据公式(3)计算此帧中的功率谱谱熵值H(m); Step4:为了防止信号突变引起误判,对功率谱谱熵值进行平滑处理,得到平滑谱熵值,平滑谱熵计算公式如下: 其中ch为平滑因子,通常取值为0.95。 Step5:利用判决门限Th进行检测,当谱熵H͂(m)在连续帧内(取5帧)大于判决门限Th(Th=4),判断为噪声,反之则为信号。 在基于谱熵的突发信号检测中,窗函数的选择对检测效果影响较大。文献[15]通过仿真分析得出结论:谱熵法选择矩形窗进行短时傅里叶变换时具有更好的检测效果,并且需保证相邻数据段的不重叠。 传统的FSK解调方法(在码元同步前提下)根据一个码元中只存在单个载频进行判断,即比较当前码元中载频f1和载频f2处的功率谱幅值,当|X(nN,K1)|>|X(nN,K2)|,则判断为载频f1对应的码元,反之为载频f2对应的码元。但实际短波通信中,存在多普勒频率、干扰和多径时延等导致载频产生偏移,简单采用固定载频估计进行解调,由于频偏误差会导致解调性能下降[16-20]。因此,文中采用寻找载频附近最大功率谱幅值的方法实现载频的最佳选择。 对信号进行短时傅里叶变换,并取载频f1和f2附近最大频偏为l处所有频谱幅度值: 研究发现,在实际FSK信号中由于噪声的干扰等因素,即使当前时刻发送的为载波f1,载频f1处的峰值不一定大于载频f2处的峰值,因此通过比较载频处最大峰值进行判决可能导致误判。但载频f1附近频段的整体频谱能量一定大于载频f2附近频段的整体频谱能量,因此采用比较频段内频谱能量具有更好的判决效果。分别求载频f1附近频段的整体频谱能量S1和S2: 比较S1和S2,当S1>S2,判断为码元 0(载频f1),否则为码元1(载频f2)。 FSK信号解调中码元同步是实现正确判决的基础。传统方法根据信号采样速率fs和估计的码元速率计算的码元宽度移动码元实现同步,由于估计误差和频偏等因素使得仅仅以码元宽度移动码元的方法解调误差较大。基于能量法判决进行码元同步的原理如图5所示。随着码元的移动,在当前码元内基于DSTFT的能量谱在一个载频中提高,在另一个载频中降低,当在一个载频中能量谱的值达到最大时实现码元同步。 图5 基于DSTFT窗移动的码元同步 基于DFT的解调方法中码元同步根据能量判决实现码元移动和同步。但传统方法采用查找载频处最大频谱值作为码元同步,研究发现[5]此方法同步精度较差,而采用谱峰比判决可实现较精确判断。假设码元宽度为N=2n,考虑极限情况下最大移动值为N/2,则每次移动一位实现同步则需要2n-1次移动,无法满足实时性要求;采用二分法[17]进行同步时,实现的粗同步影响解调分析效果。因此,文中提出了一种基于谱峰比的粗同步和细同步的码元同步方法。 Step1:取载频点附近偏移为l所有点的最大峰值: Step2:判断调整指针的方向。设前一码元为1(载频f1),如果M1(r)>M2(r) ,则向前调整,若M1(r)≤M2(r),则向后调整。 Step3:选择移动步长为N/8(则最多需移动4次)。计算每次移动后的谱峰比: 取A(r)值为最大时作为粗同步的移动位置。 Step4:进行细同步,在粗同步基础上改变移动步长为1,移动范围为粗同步窗口位置的前后N/16宽度,寻找最大峰值比A(r)为细同步位置窗口。 Step5:细同步后的窗口位置为当前码元的最终位置。根据公式(6)可进行判决和解调码元输出。 本文选择2FSK信号以MATLAB进行算法仿真分析,为了提高分析的可靠性,分别选择3种不同规格的FSK信号,其参数如表1所示。 表1 2FSK信号规格参数 为了验证谱熵方法对FSK突发信号检测的有效性,对表1中FSK1信号加不同噪声,并统计不同信噪比情况下突发信号起始时刻的检测概率。信噪比从0 dB到15 dB,步进为1 dB。在每个信噪比下对信号进行200次蒙特卡洛实验,统计不同信噪比下的检测性能,并和滑动窗口法和改进的双滑动窗法进行比较。结果如图6所示。 图6 不同信噪比下3种检测方法的性能比较 由图6可以看出,在不同性噪比情况下谱熵方法的检测性能均优于其它两种方法,尤其在信噪比小于6 dB情况下,谱熵法的检测概率明显优于其它方法。说明了谱熵法检测突发信号的鲁棒性。 为了验证本解调方法的有效性,对表1中FSK1信号加噪声,生成不同信噪比情况下的FSK信号,并和文献[5]和文献[6](此处分别命名为M1和M2)中的解调方法进行解调对比,本解调方法在此仿真中命名为M3,结果如图7所示。 图7 不同信噪比下3种检测方法的性能比较 从图7中可以看出,在信噪比较高时,由于噪声影响较小,可有效判决0或1,本方法和其他两种方法解调性能相近,但在低信噪比情况下,本方法解调性能更好。本方法采用最大载频附近能量谱比的判决方法,避免了噪声较高时的误判,同时采用选择载频附近峰值,提高了频偏对解调的影响。 实际短波FSK信号往往是突发信号,精确提取信号段可提高解调性能。为了验证基于谱熵检测的突发信号解调性能,选择表1中的3种具有突发的FSK信号进行分析,并和未进行谱熵检测直接进行解调的误码率进行对比,其中信号的信噪比为5 dB,结果如表2所示。 表2 基于谱熵检测的解调误码率对比 从表1可以看出,基于谱熵检测结合DSTFT解调的方法具有更好的解调性能。通过谱熵检测可以有效滤除噪声段,降低了噪声对解调的误判。其中FSK3信号码元速率为2 400 B。因此本方法更适合于低速率突发FSK信号的解调。 针对突发信号和短波FSK信号解调问题,通过载频附近功率谱累积量比进行码元判决,避免了噪声影响从而提高了解调性能,同时通过最大峰值比的码元同步方法提高了码元同步精度。并在解调中针对突发信号解调采用谱熵检测有效滤除了噪声段,提高了检测性能。仿真实验表明,本文所述方法针对突发FSK信号解调具有更高的鲁棒性。 [1]张孝龙.基于FPGA的软件无线电上下变频技术的研究与设计[D].南京:南京邮电大学,2013. [2]苏文盛.软件无线电下4FSK调制解调的研究及实现[D].北京:北京邮电大学,2013. [3]张鑫龙,周胜源.基于软件无线电的2FSK相干解调[J].电子设计工程,2010,18(9):118-120. [4]郭志阳,孙向阳,陈学英.基于FPGA的DSTFT算法对FSK信号解调的改进[J].电子设计工程,2016(21):4-6. [5]金文光,张正宇,唐少华.2FSK信号DSTFT解调算法中的同步新方法[J].浙江大学学报(工学版),2011,45(6):1027-1031. [6]周现国,殷素杰,徐志平.一种基于散射信道极低速率检测技术研究[J].无线电通信技术,2012,38(4):60-62. [7]徐艺文,陈忠辉,李雷,等.基于DFT的2FSK信号解调自适应门限同步检测算法[J].四川大学学报:工程科学版,2011(s1):169-173. [8]魏宇培,梁先明,廖龙灵.非协同突发信号的检测与解调[J].电讯技术,2015,55(4):395-400. [9]吴迪,葛临东,王彬.短波突发信号盲检测算法的对比研究[J].通信学报,2010(s1):111-116. [10]梁聪.短时突发信号解调算法研究[D].郑州:解放军信息工程大学,2011. [11]赵建秀,王洪国,邵增珍,等.一种基于信息熵的时间序列分段线性表示方法[J].计算机应用研究,2013,30(8):2391-2394. [12]田伟,周新力,孟庆萍,等.短波信道信噪比估计及其在信道均衡中的应用[J].系统仿真学报,2013,25(3):575-579. [13]李艳,成凌飞,张培玲.一种基于改进谱熵的语音端点检测方法[J].计算机科学,2016,43(11A):233-236. [14]魏宇培,梁先明,廖龙灵.非协同突发信号的检测与解调[J].电讯技术,2015,55(4):395-400. [15]李荣荣,胡昌奎,余娟.基于谱熵的语音端点检测算法改进研究[J].武汉理工大学学报,2013,35(7):134-139. [16]兰铂.FSK和PSK信号特征研究[D].北京:北京邮电大学,2011. [17]张骥,汤元会.基于PI调节的高稳定度交流信号源设计[J].纺织高校基础科学学报,2014,27(2):267-270. [18]同娜,朱长军,翟学军,等.两个耦合六波混频信号特性[J].纺织高校基础科学学报,2015,28(1):85-89. [19]史强强,孟新新,赵乾坤,等.数字SPWM调制信号截尾误差的补偿方法研究[J].陕西电力,2013(12):61-65 [20]马保科,常红芳,尹纪欣.电磁脉冲信号电离层传播的时间特性[J].西安工程大学学报,2016,30(6):854-860.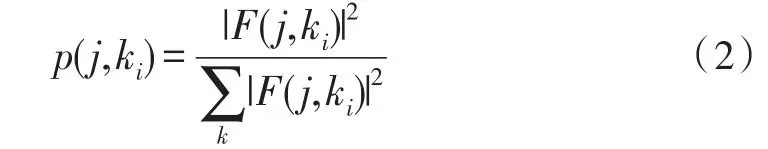
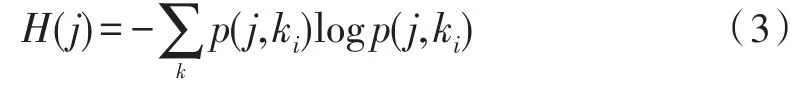
2 基于DSTFT的FSK信号解调研究
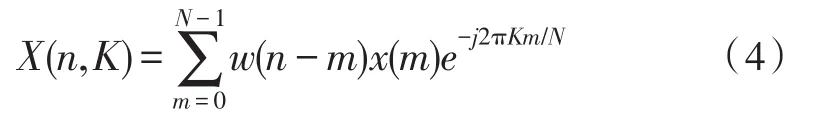

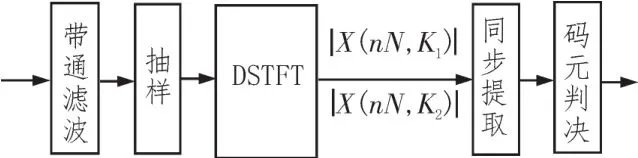

3 基于谱熵和DSTFT的突发FSK信号解调

3.1 基于谱熵的突发信号检测


3.2 抗频偏DSTFT解调


3.3 码元同步
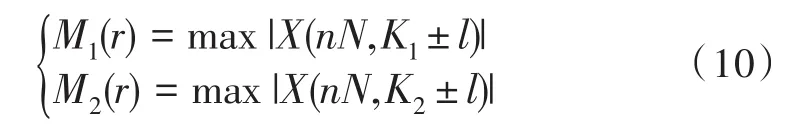

4 实验及分析
4.1 突发信号检测分析

4.2 不同信噪比下解调分析
4.3 突发检测对解调影响分析

5 结 论
