基于空载曲线反向计算的水轮发电机绕组匝间短路故障诊断方法

付廷勤，沈利平，王 罗，刘世泽，刘 伟



基于空载曲线反向计算的水轮发电机绕组匝间短路故障诊断方法

付廷勤1，沈利平1，王 罗2，刘世泽1，刘 伟1

（1. 国网甘肃省电力公司 刘家峡水电厂，甘肃 永靖 731600；2. 华北电力大学 电气与电子工程学院，河北 保定 071003）

水轮发电机中的转子绕组匝间短路在生产安全和经济方面一直困扰着水电厂。目前，水轮发电机匝间短路的故障识别多采用离线检测方法。为了解决这个问题，本文提出了基于电机基本电磁理论和反向空载曲线的诊断方法。该方法不受电机运行状态影响，通过原有电气量参数读取，如有功功率，无功功率，电压和电流，建立饱和矢量模型。利用模型计算的中间变量和空载特性曲线之间的关系来计算励磁电流的理论值。通过比较励磁电流理论值与测量值之间的差异来识别转子匝间短路故障情况。最后，采用水电站实际发电机及仿真电机验证该方法的正确性。

水轮发电机；转子绕组匝间短路；空载曲线；故障诊断；反向计算

0 前言

资料统计表明，目前运行的水轮发电机中，转子匝间短路故障占电机故障总数的比重较大[1]。大多数水轮发电机都发生过或存在转子匝间短路故障。由于该故障对机组正常运行影响不大或者故障特征不明显，所以很多匝间短路故障都没能被及时地检测和处理，但机组长期处于匝间短路情况下运行，将会导致转子线圈一点甚至两点接地，会造成发电机励磁电流增大、温度升高、转子振动加剧等不良影响。若不能尽快地处理励磁绕组短路故障，可能发展成为更加严重的事故，并对电机及整个电网的安全运行产生巨大威胁。因此进行水轮发电机匝间短路故障早期预报是十分必要的。

目前，国内外普遍采用开口变压器法微分线圈动测法[2-3]，神经网络法[4]及多回路分析法[5-6]等方法，来检测转子线圈匝间短路故障，第一种方法虽较灵敏，但属于离线检测，仅在停机且抽出转子后方能进行。多回路分析法的基本原理是，列写定转子绕组的电压、磁链方程，按照各回路的连接状态推导出电阻矩阵，并将电感矩阵中相应的电感系数计算出来，然后解出微分方程，得到各回路的电流波形。在实际情况中，水轮发电机有较多的极数与阻尼条数，这会使相关方程阶数较大，计算难度增加。同时多回路步长的选择也会影响最终结果准确与否。

在实际的水力发电厂中并不能随意添加电气量监测设备，可以直接获得的只有有功，无功功率等原有电气量。因此需要推导一种较为直接的方法利用已知电气参数诊断匝间短路故障。本文提出的空载特性曲线反向计算法不受发电机运行状态的影响，不必增加发电机新的监测点，仅通过发电机原有电气参量的读取，就可实现发电机转子匝间短路故障的在线诊断[7]。

1 发电机转子绕组匝间短路故障分析

1.1 发电机转子绕组匝间短路故障原因分析

水轮发电机转子绕组磁极多采用单层多匝线圈绕制而成，匝数从十几匝到几十匝不等，匝数与机组容量，转速有关。由于水轮发电机转子磁极较多，转子绕组额定电压不高，故线圈匝间承受的电压很低，因此单从绝缘方面考虑对匝间绝缘设计要求不高，匝间绝缘较薄弱。转子端部绕组固定不牢，垫块松动。绕组铜导线加工工艺方面的缺陷造成的不严格倒角与去毛刺等也会导致转子匝间短路。当此故障发展到一定程度时，会因匝间短路减弱发电机有效磁场，影响发电机无功出力，磁路不平衡致大轴严重磁化[8-10]。另外短路点处的局部过热可能使故障进一步扩大为转子绕组接地故障。

1.2 空载曲线反向计算法主要原理分析

空载特性曲线反向计算法在深入研究水轮发电机转子匝间短路的电磁特性基础上，基于水轮发电机基本理论和空载曲线，推导需要四种参数，即定子电流、定子电压、有功功率和无功功率计算的关系表达式。找到这些原有测量参数之间与励磁电动势，励磁电流的数学、图像等关系。利用较为精确的计算方法计算出未发生匝间短路理论励磁电流，并与实际测量励磁电流进行比较，从而判断发电机是否存在匝间短路及短路的严重程度。

2 水轮发电机励磁电流计算方法

根据图1所示的水轮发电机电磁关系，建立磁势、同步电抗、空载电动势和励磁电流的联系。同时需要做出凸极同步电机饱和时的向量图，如图2所示。根据图中关系得出凸极同步发电机空载电动势的表达式如下。

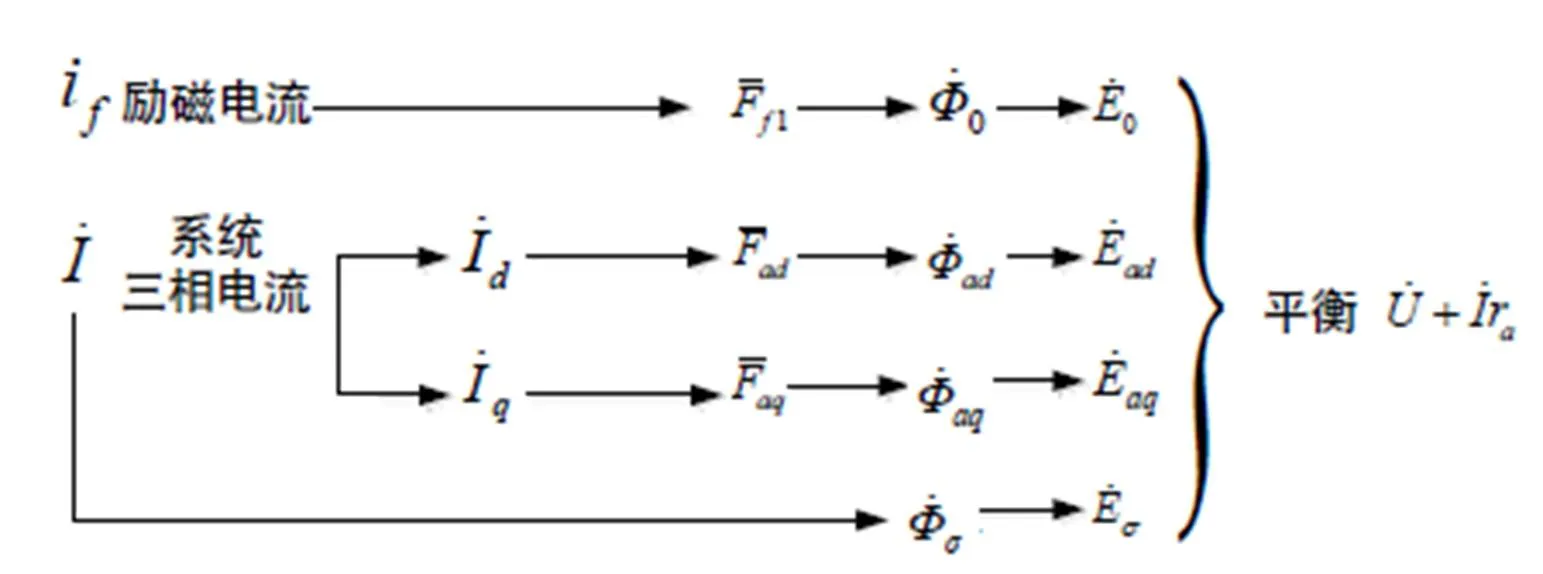
图1 电磁参数关系

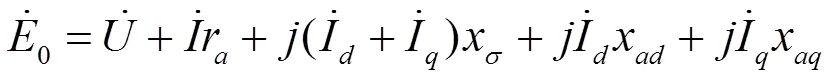
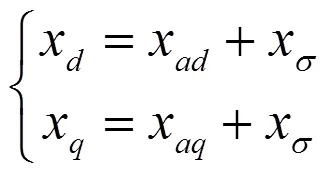
其中，0和之间夹角为。

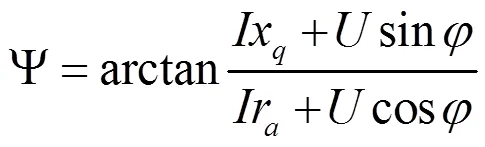
水轮发电机通常运行在正常励磁或过励状态，此时分析发电机磁场时要考虑发电机的饱和效应，以及饱和参数。根据凸极同步发电机饱和情况下的相矢图。得到如下关系

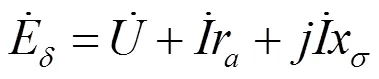
水轮发电机在实际运行情况下，定子电阻较小，一般可忽略，但本文为保证数据的准确性，考虑了定子电阻的影响。通过凸极同步电机相矢图，及相关公式，可得凸极同步电机气隙磁动势。

将气隙磁动势带入到公式（5）中可得

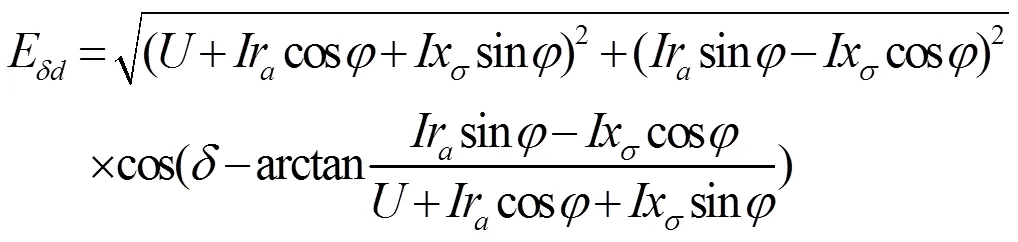
式中，r为电机定子电阻；x为电机漏电抗；为电机功率角；为电机的功率因数角。

将式（8）代入到式（6）中可得凸极发电机空载电动势。

上式即为E的计算初步表达式，但是实际可测参数中还有有功功率和无功功率没有考虑进去，通过对以上相关功率整理可得E的表达式。

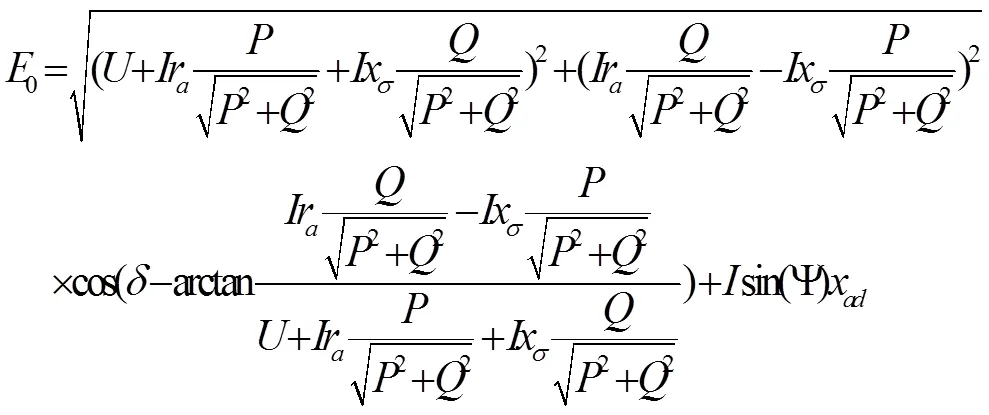
式（10）即利用已知基本电气量定子电压、定子电流、有功功率、无功功率计算励磁电动势式0的表达式。

由于在实际运行的水轮发电机处于饱和状态，直轴同步电抗X也需要考虑其影响，因此参数值将发生变化。凸极同步电机考虑饱和影响后的直轴电枢反应电抗x的值近似按下式决定

式中，k为饱和系数[11]。

同时，在这种状态下电动势0和电流I为非线性关系。对这种非线性的关系可采用空载特性曲线方法解决。一种电机的空载特性曲线只对应一种电机，同时该空载曲线不受该电机运行状态影响。因此可以利用该发电机空载特性曲线中I和0之间的对应关系，反向计算出某一确定状态励磁电流的标准值，即转子未发生故障时励磁电流的理论值。

首先利用数学软件MATLAB进行曲线拟合编程。采用甘肃省刘家峡水电站实际电机参数，绘制该电机空载特性曲线，即进行曲线拟合如图3所示，要求拟合误差小于0.1%。因此可以反向计算出在饱和情况下的励磁电流I和电动势0之间的数学表达式，即

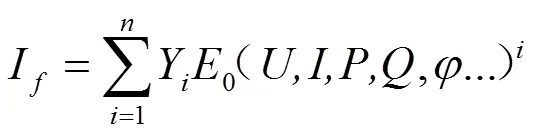
其中，Y为公式中的因数，和空载曲线有关。i为拟合曲线的次幂，对于不同的特性曲线，推导的表达式不同。在考虑到误差允许范围以及精度之后，一般采用6阶表达式模型进行拟合，其精度要求已达到要求。在本方法中需要通过E0计算If，而在空载特性曲线中自变量是励磁电流，因变量是空载电动势。因此需要反向计算，以及反向拟合曲线，将励磁电流转变为因变量进行计算。

在计算过程中根据计算的电机空载特性曲线，采用相关的参数计算出的0，再代入到公式（13）中，可以得出未发生匝间短路时的理论励磁电流，与实际测量励磁电流进行比较[12-13]，即可得出结果。

理论计算电流与实际测量电流之间计算误差公式[14-15]为

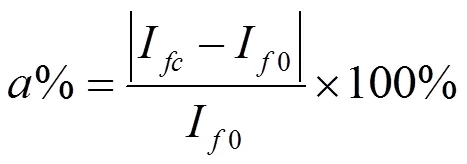
其中，I为实际测量电流；I0为理论计算电流。

3 发电机转子绕组匝间短路实验分析

本论文采用了两种验证方法：（1）正常理论计算电流与未发生匝间短路电机实测电流比较。在同一种电机不同运行状态下验证，若偏差较小可以证明该方法的准确性。（2）正常理论计算电流与已知发生匝间短路电机电流进行比较，同一运行状态，不同匝间短路情况下验证，匝间短路接近规定结果的则验证该方法的准确性。

（1）正常机组比较法，即采用刘家峡水电厂SF255-48/12640型电机2号正常机组进行了匝间短路的验证实验。SF255-48/12640机组参数见表1。刘家峡电厂2号机组未发生匝间短路故障，并处于并网运行的条件下，其有功、无功功率会发生变化。采集4组运行数据，见表2。

现选取表2中第三组数据重点论述计算方法。该电机固定参数r=0.005Ω，x=1.046，考虑饱和系数影响x会相应减小，实际中k一般取1.1~1.25。根据公式（10）带入表2第三组的数据计算0，得019.64。

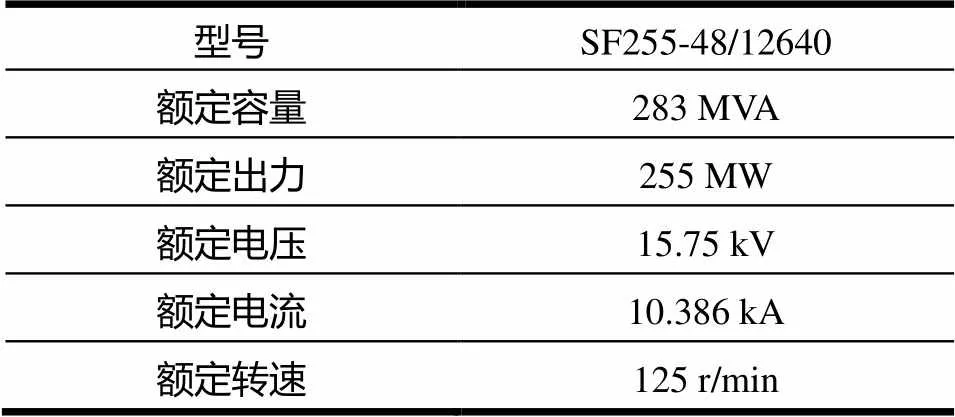
表1 刘家峡2号机组铭牌参数

表2 刘家峡正常水轮发电机运行参数及电流偏差

再根据空载曲线中0和I两者的关系进行反向计算。利用SF255-48/12640型电机2号机组的空载实验中的下降实验数据进行曲线拟合如图3所示。将该机组的空载特性对应公式（13）的表达式，确定其中的参数,利用曲线拟合工具得2号机组空载曲线反向6阶计算表达式为：

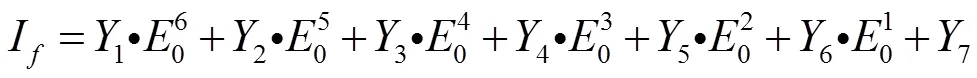
其中参数为10.000466；2-0.02587；30.5483；4-5.381；523.65；613.94；73.635。并将019.64带入到式（15）计算得到I=1365A，实际测量的转子励磁电流为1352A。

将转子电流结果带入公式（14）得实测和计算电流误差为%0.81。

同理，重新代入刘家峡2号机组的其它运行数据计算0，利用公式（14）和（15）计算得到I以及电流差值。依次进行4次参数代入，结果见表2。

刘家峡2号机组在开机实验中并未发现匝间短路故障，理论计算电流应与实测相同。考虑到参数计算的误差影响，计算电流的值与实测电流值差值在百分之一以内，较为接近。因此，该方法可以较为准确地计算未发生匝间短路时的理论正常电流。

（2）利用MATLAB仿真系统建立匝间短路电机故障模型[16]，如图4所示。通过改变模拟电机控制模块，模拟不同匝数短路的情况，并采集相关参数。再利用上述方法计算正常理论励磁电流，结果见表3。

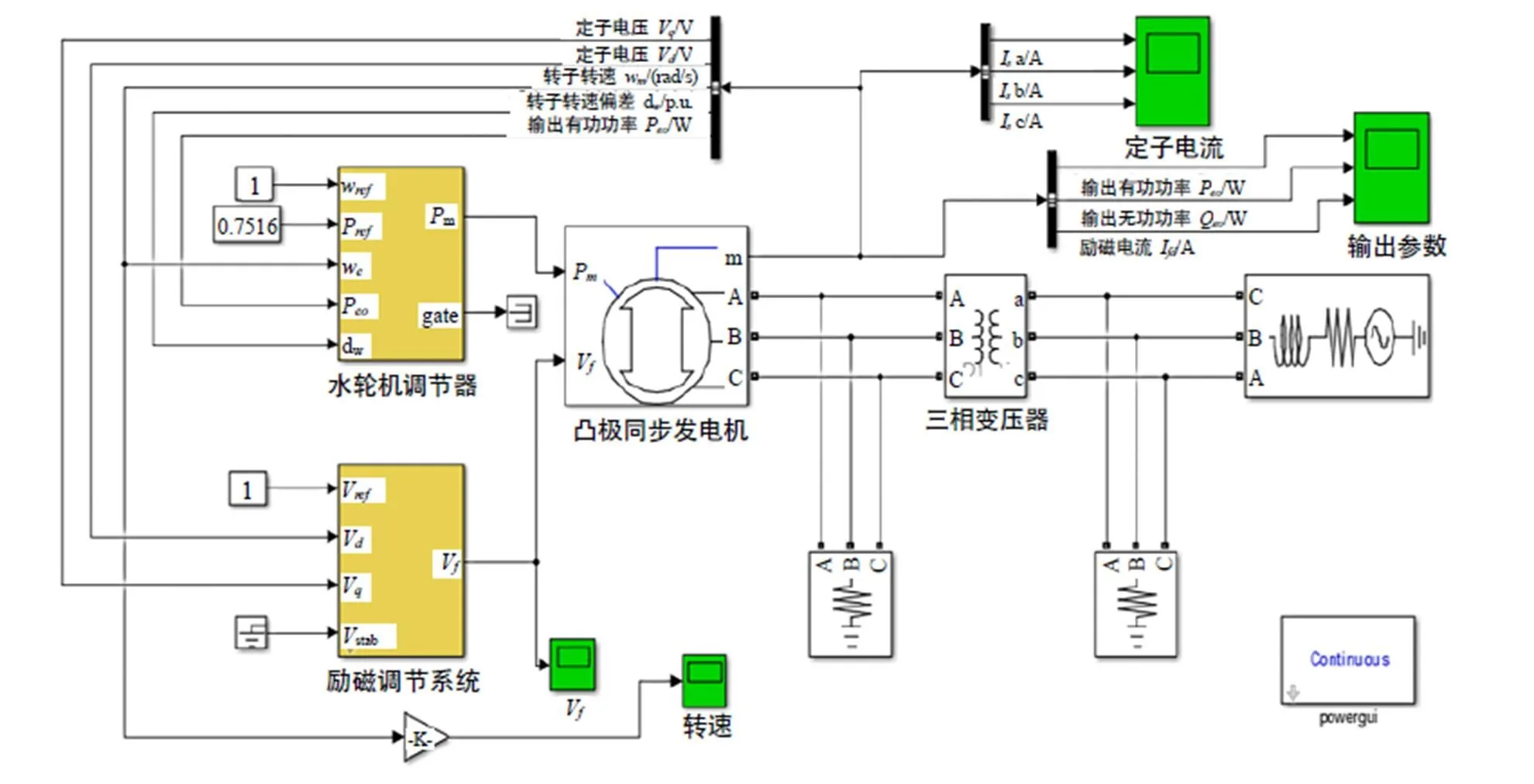
图4 水轮发电机的仿真模型

表3 模拟机组匝间短路故障参数及电流偏差

4 结论

根据刘家峡实际运行机组和模拟电机实验结果可知，空载特性曲线反向计算方法计算的正常励磁电流较为精确。如果水轮发电机转子存在匝间故障，则计算电流与其测量电流偏差值较大。并且通过偏差数值基本上可以反应其匝间短路的情况，由此可以诊断出水轮发电机是否发生匝间短路故障。

该方法是一种较为简单便捷的在线检测方法，只需测量发电机电气信息，如电压、电流、有功功率、无功功率、励磁电压等，不需要在水轮发电机上添加新的电气测量系统，不干扰发电机正常运行的情况下，即可判断水轮发电机是否存在匝间短路故障及短路的严重程度。这种检测方法对水轮发电机转子匝间短路早期诊断具有重要意义。

[1] 余文宁. 大型水轮发电机组状态监测与智能故障诊断系统研究[D]. 中南大学, 2007.

[2] 阮羚, 周世平, 周理兵. 大型汽轮发电机转子匝间短路在线监测方法的研究及应用[J]. 中国电机工程学报, 2001, 21(12):60-63．

[3] 李伟清, 王绍禹. 发电机故障检查分析及预防[M]. 中国电力出版社, 1996.

[4] 刘峰. 基于神经网络的水轮发电机组振动故障诊断专家系统的研究[D]. 河海大学, 2004.

[5] 石薇. 水轮发电机转子绕组匝间短路故障研究[D]. 华北电力大学, 2012.

[6] 郭超. 大型水轮发电机励磁绕组匝间短路的仿真研究[D]. 哈尔滨理工大学, 2014.

[7] 陈权涛, 杨向宇. 发电机转子绕组匝间短路故障在线检测方法[J]. 微电机, 2008, 41(3):65-68.

[8] 张红根. 马头电厂4号机组6号轴承振动的诊断和处理[J]. 河北电力技术, 1993(2):70-73.

[9] 郝亮亮, 孙宇光, 邱阿瑞,等. 大型水轮发电机励磁绕组匝间短路的稳态故障特征分析[J]. 电力系统自动化, 2011, 35(4):40-45.

[10] 林善明, 滕加义. 水轮发电机转子匝间短路的判断分析[J]. 科技资讯, 2012(13):117-118.

[11] 陈锡芳. 水轮发电机电磁与计算[M]. 中国水利水电出版社, 2011.

[12] Li Y G, Sun Y, Wang L L, et al. The criterion on inter-turn short circuit fault diagnose of steam turbine generator rotor windings[C]// International Conference on Electrical Machines and Systems. IEEE, 2007:1050-1054.

[13] Wan S, Xu Z, Li Y, et al. Analysis of generator vibration characteristic on rotor winding interturn short circuit fault[J]. Proceedings of the csee, 2004, 2(3):882-885 vol.2.

[14] 李永刚, 李和明, 赵华. 汽轮发电机转子绕组匝间短路故障诊断新判据[J]. 中国电机工程学报, 2003, 23(6):112-116.

[15] 李永刚, 李和明. 汽轮发电机转子匝间短路故障分析与诊断新方法[J]. 电力系统自动化, 1998(6):21-23.

[16] 贾杰. 水轮发电机转子绕组匝间短路故障的研究与识别[D]. 华北电力大学, 2015.

Diagnosis of Hydro-generator Inter-turn Short-circuit Fault Based on Reverse Calculation of No-load Curve

FU Tingqin1, SHEN Liping1, WANG Luo2, LIU Shize1, LIU Wei1

(1. Liujiaxia Hydro Power Station, Gansu Electric Power Company of State Grid Corporation of China, Yongjing 731600, China; 2. Electrical and Electronic Engineering College, North China Electric Power University, Baoding 071003, China)

Rotor winding inter-turn short circuit occurring in hydro-generators has been plaguing power producers with respect to production safety and economy. At present, fault detection methods for hydro-generators are offline or complex. To solve the problem, this paper presents diagnosis method based on electromagnetic theory and reverse no-load curve. The method is not affected by the running state of the generator. The saturation vector model is established using the original electrical quantities, such as active power, reactive power, voltage and current. Theoretical value of excitation current is calculated using the relationship between variables calculated by the model and no-load characteristic curve. Inter-turn short circuit fault situation is identified by comparing the difference betweenthe normal calculated excitation current and the measured excitation current. At last, the correctness of this method is verified by the experiment of hydropower plant actual generator and simulation generator.

hydro-generator; inter-turn short circuit of rotor winding; no-load curve; fault diagnosis; reverse calculation

TM307+.1

A

1000-3983(2018)02-0027-05

2017-05-06

付廷勤，（1969-），1992年7月毕业于武汉水利电力学院动力工程专业，现从事水电机组研究工作，高级工程师。