基于解析单元方法的土壤水渗透量数值模拟试验分析

2018-03-29张生宇

水利技术监督 2018年2期

张生宇

(辽宁省水文局，辽宁沈阳 110000)

土壤水渗透量分析和计算对于探索作物需水规律至关重要。当前，国内有许多学者展开土壤水渗透量的观测试验分析[1- 4]，该方法可较好的对土壤水渗透量进行准确观测，这种方式不能实现土壤渗透水量时空分布的计算。近些年来，有学者应用数值求解方法对土壤水渗透量的计算[5- 6]，计算精度不高，计算误差一般在20%～30%之间。目前，解析单元方法由于可下渗水体进行分段计算，在河流水力学中得到应用[7- 10]，计算精度较高，但在土壤水渗透量数值求解中还未得到相关应用，为此本文引入解析单元方法，结合辽宁中部某试验区监测的土壤水渗透数据，分析解析单元方法在土壤水渗透量数值计算中的适用性。

1 解析单元方法计算原理

解析单元方法将土壤入渗水体当成线性汇流的水体，将整个土壤下渗水体进行分段计算，计算方程为：

(1)

式中，Q(i)—分段土壤水下渗水量，m3；Yi—不同分段的土壤水水位，m；K—计算的土壤水势；i—分段数。

按单位分段对土壤下渗水量进行单段转换，转换方程为：

(2)

式中，e—土壤水汇集的水量，m3。在方程求解时采用数值积分的方法进行求解，求解方程为：

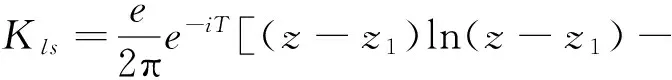
(3)

式中，T—计算时段，z、z1、z2—分段计算的土壤水势能。

2 土壤水渗透量数值模拟精度试验

2.1 试验区域概况

试验区集水面积为145km2，位于辽宁省中部平原区，该试验区对土壤水渗透量进行长系列的观测试验，区域多年平均降水量为600～800mm，多年平均径流深300～400mm，试验区土质主要为壤土，土壤水渗透观测数据系列长度为2002～2012年，并对月土壤下渗水量进行了观测。本文结合区域监测的土壤水渗透观测试验数据，对比解析单元方法在土壤水渗透量数值模拟的适用性。

2.2 参数无偏估计

在进行土壤水渗透量数值计算前，首先采用极大熵谱方法对解析单元方法中的计算分段参数i进行了无偏估计计算，分析结果见表1。

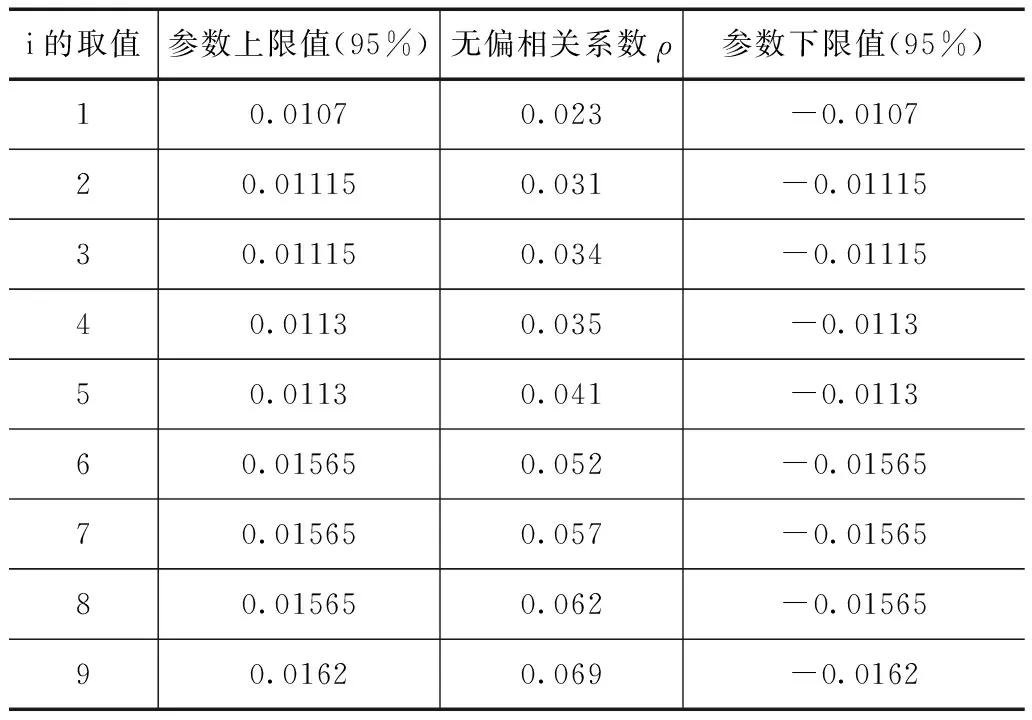
表1 模型参数无偏估计结果

从表1可以看出，随着计算分段i的增加，无偏相关系数ρ均逐渐递增，从0.023递增到0.069，且均可通过参数上限和下限置信度水平95%的检验，表明当i增加到9时，参数达到最优化，也较为合理。可见，当解析单元分段数越多，其参数结果越为合理，当解析单元分段数达到9段以上，其计算效果最佳，为此本文选用i=9确定为解析单元方法的数值求解的分段参数。

2.3 土壤水渗透量数值模拟结果

在进行参数无偏估计后，结合解析单元方法对试验区年尺度和月尺度的土壤水渗透量进行预测，并结合试验观测的年土壤水下渗量和月土壤水下渗量对比分析解析单元方法的计算精度，结果见表2、3以及图1。

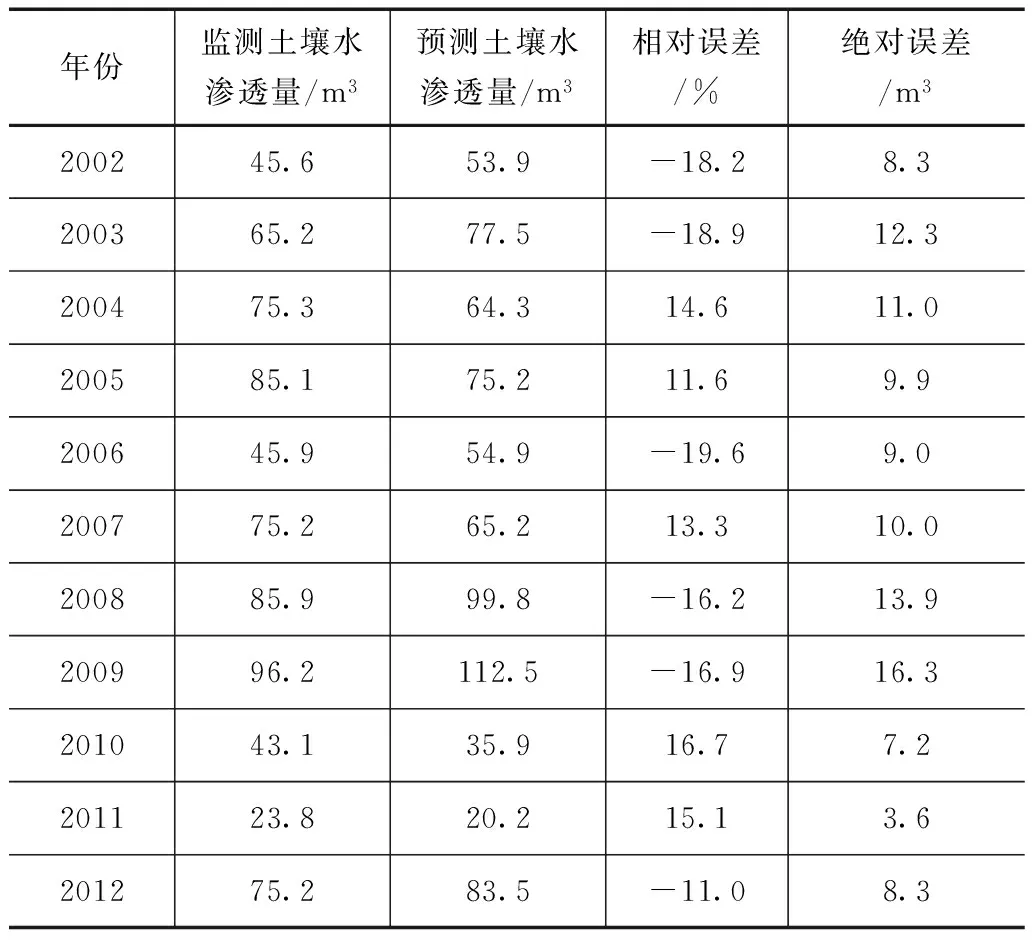
表2 年尺度渗透水量预测结果

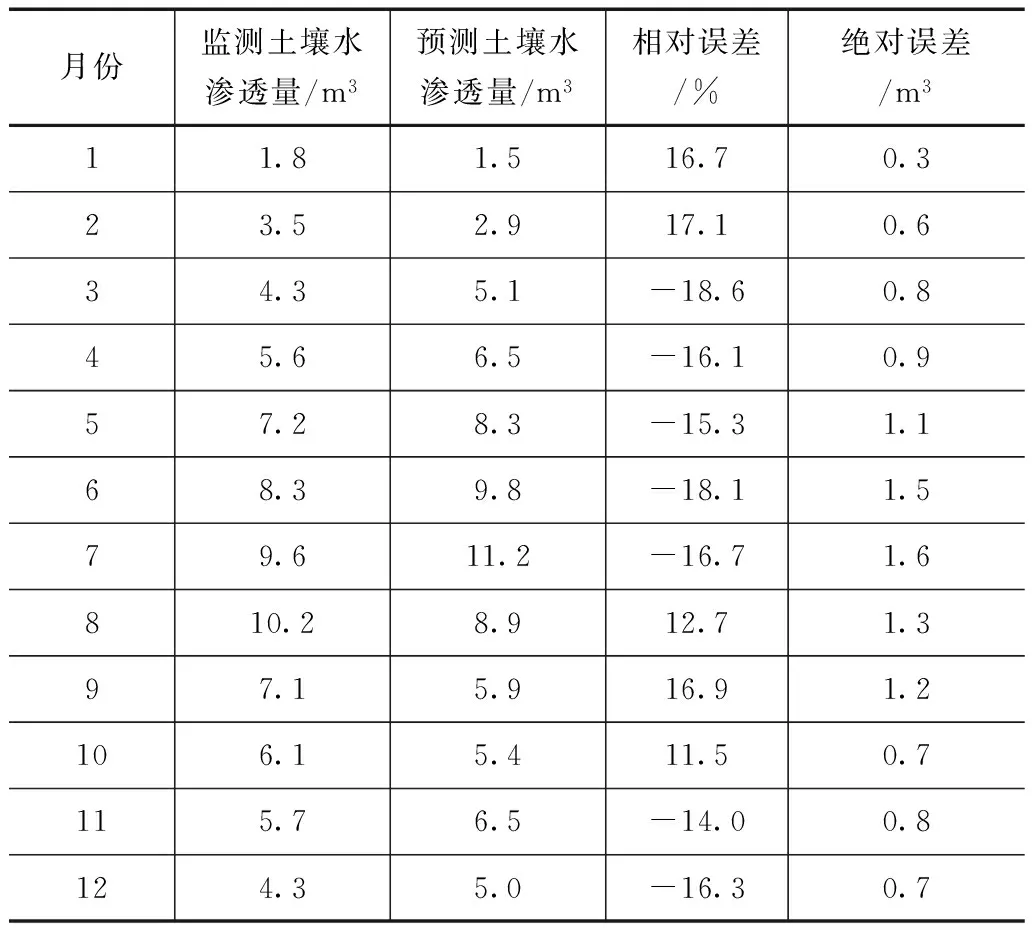
表3 月尺度渗透水量预测结果

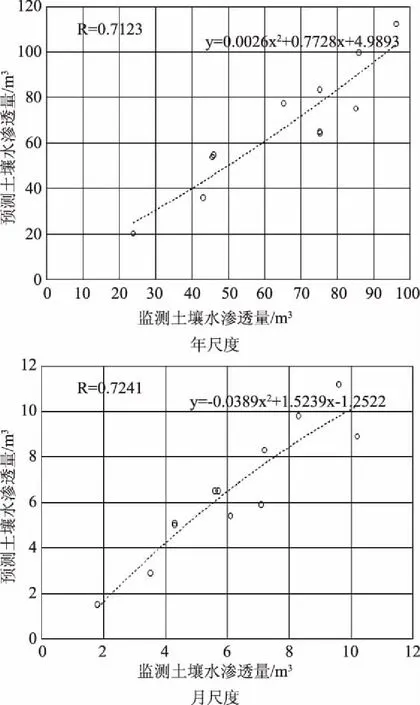
图1 解析单元方法计算土壤水渗透量和监测土壤水渗透量相关度分析结果

从表2可以看出，采用解析单元方法预测的年土壤水渗透量和试验观测的各年份土壤水渗透量之间的误差在-11.0%～-19.6%之

间，小于20%，误差绝对值在3.6～16.3m3之间。表3为采用解析单元方法预测的月土壤水渗透量和试验观测的各月土壤水渗透量之间的精度结果，从表中可以看出，各月份的误差相对值在11.5%～-18.6%之间，也均小于20%，计算误差绝对值在0.3～1.6m3之间。从误差对比结果可以看出，月尺度和年尺度相对误差较为相近，但月尺度误差绝对值好于年尺度误差绝对值。从预测值和试验观测值的相关度分析结果可以看出，年尺度和月尺度相关系数分别为0.7123和0.7241，较为接近。综上，解析单元方法在试验区土壤水渗透数值模拟精度较高，可用于农田水利规划区域垂向分布的土壤水渗透量的数值模拟计算。