深水盆地高温高压环境下的地层压力预测方法

彭海龙 刘 兵 赫建伟 李文拓 吴云鹏

中海石油（中国）有限公司湛江分公司

0 引言

地层孔隙压力和破裂压力是油气勘探开发中非常重要的参数，是钻井液密度、井身结构等多项钻井工作设计的依据。地层压力预测不准确常常会给钻井工作带来一系列的问题，比如井涌、井壁失稳、卡钻、井眼报废等问题，严重时甚至导致火灾和井喷，造成安全事故。因此，研究和开发能准确预测地层压力的计算方法对指导钻井施工非常重要。

目前，国内外常用的孔隙压力计算算法有Eaton法、等效深度法、经验公式法、压实趋势线法、有效应力法[1-4]。这些方法均需要建立正常压实趋势线[5]，运用较广，对于欠压实作用形成的超压预测效果较好。Fillippone法[6]、刘震法[7]等方法不需要建立正常压实趋势线[8]，预测精度较低，但是适合于勘探成熟度较低的工区。计算破裂压力常用算法有Eaton法、Stephen法、黄荣樽法、Holbrook法[9-11]等。孔隙压力计算方法的地层压力预测模型由于理论公式存在局限性[12-14]，在实际使用过程中通常假设砂岩段具有和邻近泥岩段相似的地层压力，同时由于多因素形成的“他源”超压现象，致使孔隙压力计算方法的预测结果较差；对于破裂压力的计算方法，由于其假设岩层的抗张强度为零，且设定岩层泊松比为常数，实际上这些假设在深水高温高压复杂地质区域是不成立的，因而在该地区的应用效果不太理想。

南海琼东南深水盆地由于地层高温、高压、地质构造复杂、断块发育等因素，地层压力分布十分复杂。研究表明，除了常规欠压实作用导致的超压之外，盆地内泥底辟、断层、砂体等特殊地质体的存在，常常使深度超压与浅层窜通，致使形成浅层高压，导致局部超压面深度起伏较大。现有的钻前地层压力预测误差大，难以满足钻井要求。根据南海深水超压盆地的地质特点及常用地层压力计算方法，考虑不同区域的压实背景差异性，通过分构造和分区域建立压实趋势线，改进常规经验公式法，计算地层孔隙压力；进而在调研工区物性参数分布规律的基础上，改进了Stephen方法计算地层破裂压力的参数，提高了其计算结果精度；最后设计程序模块，建立了软件预测平台。该平台成功应用于琼东南盆地20余口高温高压深水探井的钻前压力预测工作中，为深水环境勘探工作的顺利实施提供了技术支持。

1 地质背景

琼东南盆地位于海南岛与西沙群岛之间，总体呈北东向展布，面积8×104km2。海水由西北向东南变深，陆架区水深介于90～200 m，陆坡向西沙海槽水体急剧加深，从200 m迅速加深至2 000 m左右。盆地在演化过程中，其经历的应力场以张性为主，是一个快速沉降的新生代沉积盆地。新生代以来，地壳多次强烈拉张，盆地沉降快，沉积厚度大，由于快速的沉积速度和较低的压实速率，形成了异常高压，在盆地的中央位置，地温梯度高达42 ℃/km，地层的压力系数最高2.35，为典型的高温高压盆地[15]。晚中新世以后，持续沉降和细微的构造运动是维持异常高压的条件之一[16-17]。研究发现，盆地内异常地层压力普遍存在，而且超压顶深在盆地内横向分布变化较大，不同区域内的底辟构造带超压顶深相差也很大，且超压出现突然，过渡带薄，在底辟构造带中实测压力往往比预测值要大得多[18-20]。

2 深水高温高压地层钻前压力预测面临的问题

在琼东南盆地的浅水区，已有的压力预测技术取得了较为显著的成果，在深水区域，地层压力预测面临着以下几方面的问题：

1）盆地地质条件复杂，受复杂断块和岩性突变以及构造运动等影响，异常压力带分布无规律。盆地边缘发现异常压力较少，异常高压的顶较深，向着盆地中央超压逐渐增加，异常高压顶变浅，异常压力的顶部起伏较大；且压力的过渡带不明显，出现异常压力系数突然增加的现象较普遍。

2）盆地地层压力成因多变，预测困难。该区域背景压实规律复杂多变，盆地中异常高压的主要原因是压实作用，在压实作用基础上常常形成他源超压。由于地质因素的影响，地层压力系数不一定随埋深增加，在浅层形成异常高压，导致可预测性差。同时由于莺琼盆地的整体勘探程度较低，区域内已钻井较少，很难从区域地质体的纵向和横向上掌握层速度变化趋势，进一步加大了压力预测的难度。

3）目前常用的方法都存在一定的局限性，使得预测结果和实测结果误差大。经验法预测钻前压力在浅水区域已证实为精度比较高的方法，但是常规经验公式法压力预测仅考虑地层速度与正常压实趋势的差异性，在使用时应用一个压实趋势进行压力预测，然而在深水高温高压区域中，不同区域、不同构造的正常压实趋势往往是有明显差异的，尤其是在超压层段。因此，采用同一压实趋势进行压力预测必然会导致较大的误差。应用Stephen法计算地层破裂压力时，对地层的抗拉强度以及泊松比的取值考虑不足，也致使破裂压力的预测精度不高。

以上问题的存在，对压力预测带来很大的困扰，特别是常规压力预测方法的局限性，影响了琼东南深水盆地的油气钻探工作。

3 地层压力预测方法

为了提高地层压力预测的精度，在分析常规经验公式法原理的基础上，充分考虑区域压实背景的多样性，引入不同区域、不同构造的正常压实速度趋势线，计算孔隙压力；对于破裂压力，在Stephen公式的基础上，引入地层抗张强度，改变公式中泊松比参数的取值方式，计算地层破裂压力。

3.1 孔隙压力计算方法

常规经验公式法由P.Bellotti[21]在1987年提出，也称为速度地层因子法。作者在常规经验公式法的基础上，对相关计算方法和流程进行了改进，其计算流程主要步骤为以下3步。

3.1.1 分区域、分构造建立正常压实速度趋势线

常规经验公式法通常选择地层中泥质含量较多的地层段内的速度曲线作为压实曲线[22]，具体步骤为：①通过多井的速度—深度交汇图，选定沉积环境稳定的泥岩段数据，拟合出泥岩段的深度—速度关系；②通过经验公式法计算孔隙压力。

对于一个沉积盆地内的局部范围，沉积物都会经历沉积、埋藏到成岩等过程。浅层地层的沉积演化也包含上述的所有过程，且沉积过程中不受自源或他源因素干扰，可以认为是处于正常压实阶段。因此，作者从地质沉积角度出发，选择浅层的地层速度作为正常压实速度趋势线。考虑到区域差异性，对不同的目标区域浅层地层速度进行拟合得到不同区域及不同构造正常压实速度趋势线。以上述条件为基础，对正常压实速度趋势线的建立进行简化处理，选定目标靶区内参考井的浅层声波数据作为正常压实段，拟合该层位的速度趋势线作为正常压实速度趋势线，如图1所示。

分析图1中的地震剖面，琼东南盆地浅部地层第四系乐东组及以上地层，在剖面上的反射同相轴连续，其地质沉积环境稳定。而新近系上新统莺歌海组以及之下的新近系中新统黄流组的地震反射同相轴不连续，振幅弱，较难判定其沉积环境的稳定性。因此选择乐东组及以上的地层速度作为该区域的背景速度趋势线，采用高阶多项式拟合，将拟合结果和原始速度曲线进行叠合显示，寻找到最为符合浅层速度曲线的拟合趋势线，如图1右图所示。由图1右侧的拟合结果，得出该区域的背景速度趋势线公式为：

式中h表示地层深度，m；vh表示地层深度h所对应的正常压实速度，m/s。

3.1.2 定义速度异常值与压力系数关系

速度异常值（Δv）表示速度差值，就是正常压实趋势线速度和真实地层速度之间的差值，压力系数通过已钻井的测压数据统计得到。根据已有的压力系数和速度数据，结合建立的趋势线数据，可以统计出不同构造和区域的速度异常值和压力系数关系图（图2），其关系式为：

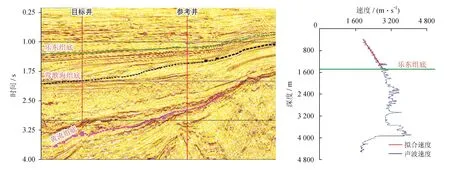
图1 琼东南盆地目标井正常压实速度趋势速度拟合图

图2 速度异常值与压力系数关系图

式中vi、vn分别表示实际地层层速度和正常压实趋势线上的层速度，m/s；Δv表示速度异常值，m/s。

3.1.3 计算孔隙压力

经实际测试，速度异常值和地层孔隙压力之间具有较好的线性关系，地层孔隙压力计算公式为：

式中pp表示孔隙压力，MPa；ak、bk示不同异常值范围内的线性公式系数；Δvi表示当前地层深度位置处的速度异常值，m/s。

该公式的提出，大大简化常规经验公式法预测孔隙压力流程，提高了工作效率。该方法的流程如图3所示。

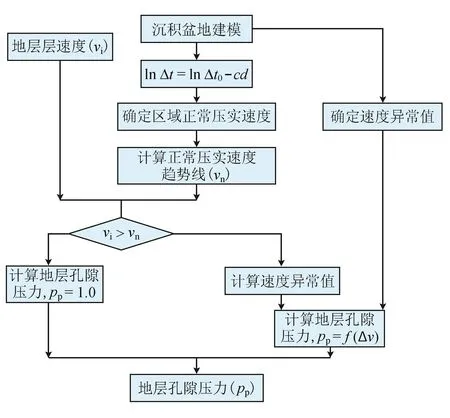
图3 孔隙压力计算流程图

3.2 破裂压力计算方法

在Stephen公式的基础上，改进方法引入了地层抗张强度。计算公式为：

式中pf表示破裂压力，MPa；u表示泊松比；K表示构造应力系数，MPa，取值范围为0～0.5；po表示上覆压力，MPa；St表示地层抗张强度，MPa，取值范围为0～0.1。

Stephen公式计算破裂压力时，泊松比为常数。然而利用岩心测试数据对盆地纵横波地震参数进行分析对比之后，发现泊松比在不同的岩性和深度范围内具有不同的特性。当地层深度达到一定深度后，纵横波速度比和泊松比基本不受深度的影响，泊松比为一个常数[23]。利用泊松比的特性分段计算破裂压力，改进以往只采用固定泊松比作为破裂压力计算条件的不足，根据区域内泊松比的分布规律，建立了泊松比随深度变化的经验公式，按照泊松比的特性对破裂压力进行分段计算。

根据岩石力学理论，引入动态岩石力学参数模型计算泊松比，计算公式为：

式中u(h)表示动态泊松比，无量纲；Δts表示横波时差，s；Δtp表示纵波时差，s。

将公式（5）引入公式（4）中，则变为：

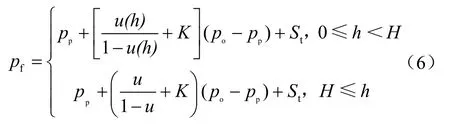
公式（6）中采用密度积分方式计算上覆压力[po(h)]，其计算公式为：

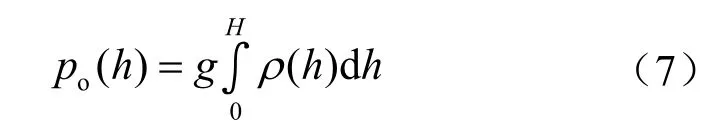
式中g表示重力加速度，m/s2；ρ表示地层密度，g/cm3。

Traugott给出了平均密度(ρav)公式：

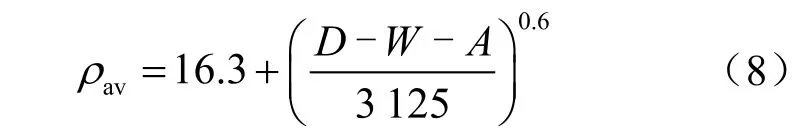
式中ρav表示平均密度，ppg（1 ppg = 0.119 826 g/cm3，下同）；D表示垂直地层深度，ft；W表示水深，ft（1 ft = 25.4 mm，下同）；A表示补心高度，ft。

计算准确的上覆地层压力时需要全井段密度曲线，然而要实测全井段密度曲线很难。因此，可以采用Amoco公式和Gardner公式来拟合缺失段的密度曲线[24-26]，拟合公式为：

式中ρmudline表示起始沉积的密度，g/cm3；A和B表示拟合参数。公式（9）为Amoco公式；公式（10）为Gardner公式。

拟合完毕之后，选择合适的拼接范围将原始密度和计算密度进行拼接，得到全井段密度曲线，也可以对全井段采用拟合的密度曲线进行计算。最后通过参考井与目标井在地层上的对应关系进行移动得到目标井的密度曲线，上述方法为上覆压力的计算奠定了基础。密度拟合示意图如图4所示。

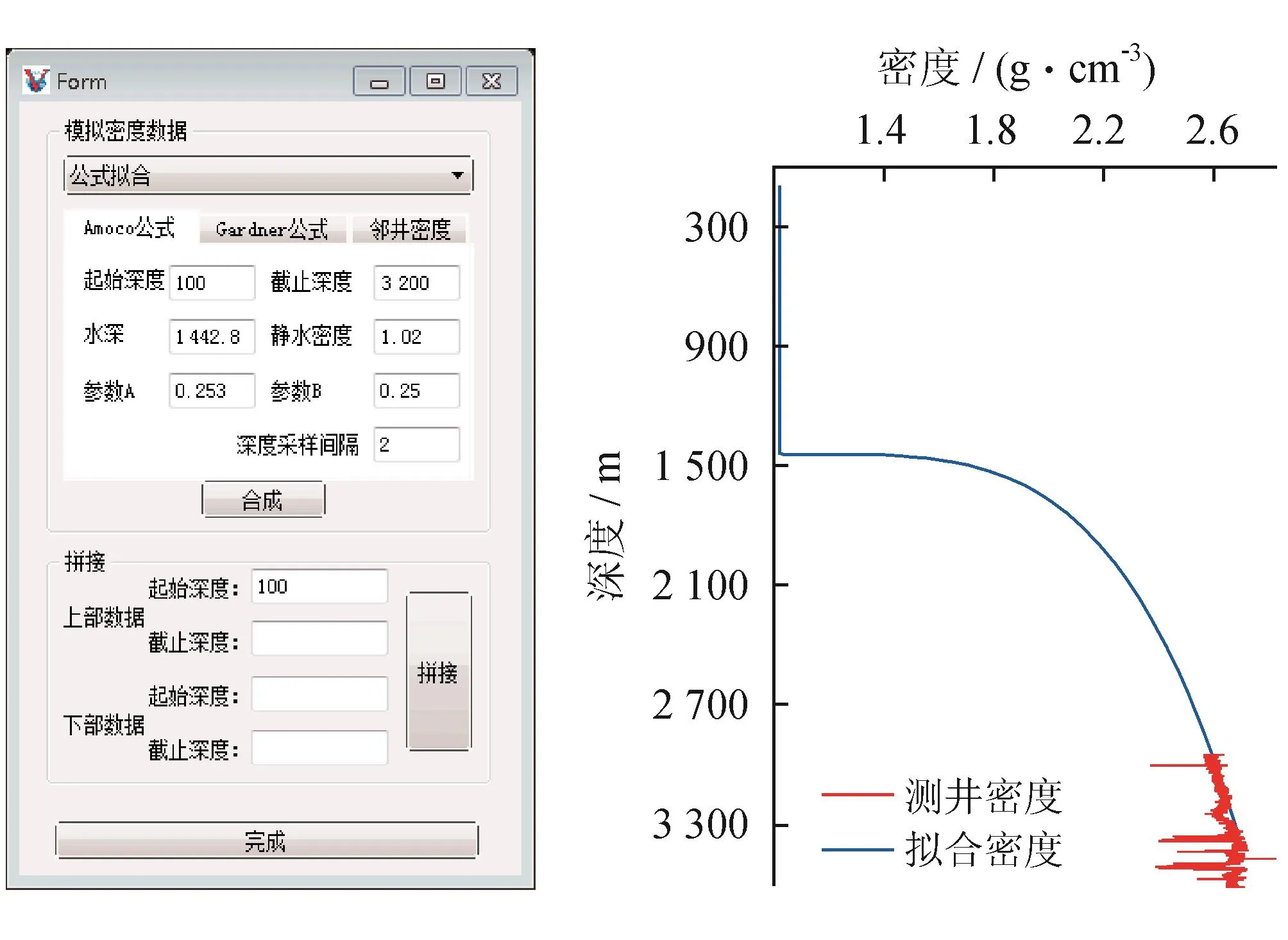
图4 密度拟合图

4 应用实例

4.1 工区情况

陵水A构造位于琼东南盆地深水区中央峡谷内，水深1 500 m左右，主要目的层中新统黄流组埋深3 200 m左右，地层温度90 ℃左右，地层压力系数1.5左右，储层为多期浊积水道砂岩。

4.2 应用效果

采用改进的经验法公式对目标井进行压力预测，在目的层预测孔压数值与完井后实际测压值匹配较好，改进的Stephen预测的破裂压力与实测地漏点较为吻合（图5）。

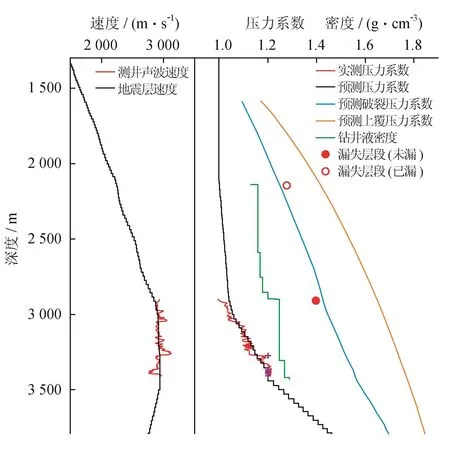
图5 A井钻前钻后压力数值对比图

近年来，南海西部探区的地层压力预测在琼东南深水盆地应用较多，对多口高温高压新探井进行了钻前预测，通过跟踪预测井后期的试油压裂的生产情况，地层的预测压力和实测压力数据吻合良好，相对误差在5%以内（表1）。

分析表1可知，测压点数据所在位置深度及压力成因类型都会影响地层压力的预测结果。当工区内已钻井测压数据较多，井位分布位置较为理想，目标井和参考井的压力成因情况类似，则目标井的预测结果较为准确。

表1 钻前钻后压力系数计算误差统计表

5 结论

1）对测井速度和地层沉积相之间的关系进行分析，分区域、分构造建立正常压实趋势线，改进了趋势线建立方法。新的方法不需要对当前工区内的岩性做出判断，直接对目标区域浅层正常压实范围内进行速度拟合，提高了工作效率和预测精度。

2）泊松比在不同的岩性和深度范围内具有不同的特性，当地层深度达到一定深度后，纵横波速度比和泊松比基本不受深度的影响，泊松比的这一特性可用于分段计算破裂压力，新的破压计算模型比常规的Stephen方法更适合深水区，提高了目标靶区破裂压力的预测精度。

3）将改进的常规经验公式通过编程设计开发压力预测平台，用于实际生产，新方法预测结果误差小，精度高，可用于南海北部深水盆地高温高压环境下的勘探设计井的钻前压力预测，满足设计要求，具有良好的应用前景。

[ 1 ] 杨振平, 吴波, 王勇. Eaton法预测M油田地层孔隙压力[J].石油天然气学报, 2012, 34(9): 181-187.Yang Zhenping, Wu Bo & Wang Yong. Application of Eaton method in predicting the formation pore pressure of M oilf i eld[J].Journal of Oil and Gas Technology, 2012, 34(9): 181-187.

[ 2 ] 陈胜, 赵文智, 欧阳永林, 曾庆才, 杨青, 侯华星, 等. 利用地球物理综合预测方法识别页岩气储层甜点——以四川盆地长宁区块下志留统龙马溪组为例[J]. 天然气工业, 2017, 37(5):20-30.Chen Sheng, Zhao Wenzhi, Ouyang Yonglin, Zeng Qingcai, Yang Qing, Hou Huaxing, et al. Comprehensive prediction of shale gas sweet spots based on geophysical properties: A case study of the Lower Silurian Longmaxi Fm in Changning Block, Sichuan Basin[J]. Natural Gas Industry, 2017, 37(5): 20-30.

[ 3 ] Fillippone WR. On the prediction of abnormally pressured sedimentary rocks from seismic data[C]//Offshore Technology Conference, 30 April-3 May 1979, Houston, Texas, USA.

[ 4 ] 张兆辉, 姚军, 苏明军. 井—震拟合反演压力系数技术及应用[J]. 天然气地球科学, 2016, 27(4): 739-744.Zhang Zhaohui, Yao Jun & Su Mingjun. Logging and seismic fi tting inversion pressure coeff i cient technology and its application[J]. Natural Gas Geoscience, 2016, 27(4): 739-744.

[ 5 ] 屈大鹏, 陈超, 王明飞, 苏建龙. 川东南地区基于海相泥页岩地层的压力系数预测——以丁山区块为例[J]. 物探与化探,2016, 40(2): 349-352.Qu Dapeng, Chen Chao, Wang Mingfei & Su Jianlong. Researches based on the prediction methods of marine-shale pressure coefficients in southeastern Sichuan Basin: A case study of DS area[J]. Geophysical and Geochemical Exploration, 2016, 40(2):349-352.

[ 6 ] Fillippone WR. Estimation of formation parameters and the prediction of overpressures from seismic data[C]//1982 SEG Annual Meeting, 17-21 October 1982, Dallas, Texas, USA.

[ 7 ] 刘震, 张万选, 张厚福, 邓祖佑. 辽西凹陷北洼下第三系异常地层压力分析[J]. 石油学报, 1993, 14(1): 14-24.Liu Zhen, Zhang Wanxuan, Zhang Houfu & Deng Zuyou. An analysis of abnormal formation pressures of Paleogene in the north sag of Liaoxi Depression[J]. Acta Petrolei Sinica, 1993,14(1): 14-24.

[ 8 ] 吴波, 王荐, 潘树林, 赵爽. 基于高低频速度闭合技术的地层压力预测[J]. 石油物探, 2017, 56(4): 575-580.Wu Bo, Wang Jian, Pan Shulin & Zhao Shuang. Formation pressure prediction based on a closed velocity body by merging the high frequency velocity with the low frequency velocity[J]. Geophysical Prospecting for Petroleum, 2017, 56(4): 575-580.

[ 9 ] Zhang Jincai. Pore pressure prediction from well logs: Methods,modifications, and new approaches[J]. Earth Science Reviews,2011: 108(1-2): 50-63.

[10] 周拿云, 杨兆中. 地层破裂压力预测技术综述[J]. 重庆科学技术学院学报(自然科学版), 2011, 13(1): 36-39.Zhou Nayun & Yang Zhaozhong. Overview on pressure prediction of formation fracture[J]. Journal of Chongqing University of Science and Technology (Natural Sciences Edition), 2011, 13(1):36-39.

[11] 张伟, 邓嵩, 樊洪海, 王国斌, 申延晴, 沈维格. 地层破裂压力三维计算与显示方法[J]. 科学技术与工程, 2014, 14(34): 140-144.Zhang Wei, Deng Song, Fan Honghai, Wang Guobin, Shen Yanqing & Shen Weige. 3D calculation and display for formation fracture pressure[J]. Science Technology and Engineering, 2014,14(34): 140-144.

[12] 罗黎敏, 胜亚楠, 刘晓坡, 管志川, 刘书杰, 冯桓榰. 含可信度地层破裂压力的钻前预测方法[J]. 断块油气田, 2017, 24(1):112-115.Luo Limin, Sheng Yanan, Liu Xiaopo, Guan Zhichuan, Liu Shujie & Feng Huanzhi. Pre-drilling prediction of fracture pressure with credibility[J]. Faul-Block Oil & Gas Field, 2017, 24(1): 112-115.

[13] 夏宏泉, 张元泽, 陈平, 刘之的, 范翔宇. 碳酸盐岩地层破裂压力的测井预测研究[J]. 天然气工业, 2004, 24(8): 32-35.Xia Hongquan, Zhang Yuanze, Chen Ping, Liu Zhide & Fan Xiangyu. Log prediction of carbonate formation breakdown pressure[J]. Natural Gas Industry, 2004, 24(8): 32-35.

[14] 李昌盛, 宋海, 肖莉, 杨传书, 徐术国. 基于遗传算法优化BP神经网络的地层破裂压力预测方法[J]. 西安石油大学学报(自然科学版), 2015, 30(5): 75-79.Li Changsheng, Song Hai, Xiao Li, Yang Chuanshu & Xu Shuguo. Prediction method of formation fracture pressure based on BP neural network optimized by genetic algorithm (GA)[J]. Journal of Xi'an Shiyou University (Natural Science Edition), 2015,30(5): 75-79.

[15] 谢玉洪. 南海北部自营深水天然气勘探重大突破及其启示[J].天然气工业, 2014, 34(10): 1-8.Xie Yuhong. A major breakthrough in deepwater natural gas exploration in a self-run oil/gas fi eld in the northern South China Sea and its enlightenment[J]. Natural Gas Industry, 2014, 34(10):1-8.

[16] 王振峰, 胡代圣. 莺歌海盆地中央泥拱构造带大气田勘探方向[J]. 天然气工业, 1999, 19(1): 28-30.Wang Zhenfeng & Hu Daisheng. Prospecting for giant gas fi elds in the central mud diapir structure belt in Yinggehai Basin[J].Natural Gas Industry, 1999, 19(1): 28-30.

[17] 王振峰, 罗晓容. 莺琼盆地高温高压地层钻井压力预监测技术研究[M]. 北京: 石油工业出版社, 2004.Wang Zhenfeng & Luo Xiaorong. Research of drilling pressure prediction and dectection method in high temperature and high pressure formation of Yingqiong Basin[M]. Beijing: Petroleum Industry Press, 2004.

[18] 刘全稳, 何家雄, 陈国民. 莺歌海盆地中深层天然气成藏特征[J]. 天然气工业, 2005, 25(9): 1-3.Liu Quanwen, He Jiaxiong & Chen Guomin. Gas reservoiring characteristics of the medium-deep strata in Yinggehai Basin[J].Natural Gas Industry, 2005, 25(9): 1-3.

[19] 谢玉洪, 李绪深, 徐新德, 童传新, 熊小峰. 莺—琼盆地高温高压领域天然气成藏与勘探大突破[J]. 中国石油勘探, 2016,21(4): 19-29.Xie Yuhong, Li Xushen, Xu Xinde, Tong Chuanxin & Xiong Xiaofeng. Gas accumulation and great exploration breakthroughs in HTHP formations within Yinggehai-Qiongdongnan Basins[J].China Petroleum Exploration, 2016, 21(4): 19-29.

[20] 王振峰, 孙志鹏, 张迎朝, 郭明刚, 朱继田, 黄保家, 等. 南海北部琼东南盆地深水中央峡谷大气田分布与成藏规律[J]. 中国石油勘探, 2016, 21(4): 54-64.Wang Zhenfeng, Sun Zhipeng, Zhang Yingzhao, Guo Minggang,Zhu Jitian, Huang Baojia, et al. Distribution and hydrocarbon accumulation mechanism of the giant deepwater Central Canyon gas fi eld in Qiongdongnan Basin, northern South China Sea[J].China Petroleum Exploration, 2016, 21(4): 54-64.

[21] 马启富. 超压盆地与油气分布[M]. 北京: 地质出版社, 2000.Ma Qifu. Overpressured basin with the oil and gas distribution[M]. Beijing: Geological Publishing House, 2000.

[22] 张发强, 王震亮, 吴亚生, 杨计海, 罗晓容. 消除影响压实趋势线地质因素的方法——以莺歌海盆地为例[J]. 沉积学报,2002, 20(2): 326-332.Zhang Faqiang, Wang Zhenliang, Wu Yasheng, Yang Jihai & Luo Xiaorong. A method for eliminating geology factors of affecting compaction trendline: An example from Yinggehai Basin[J]. Acta Sedimentologica Sinica, 2002, 20(2): 326-332.

[23] 张树林, 姜立红. 莺琼盆地岩石弹性物性规律的研究[J]. 物探化探计算技术, 2001, 23(4): 308-313.Zhang Shulin & Jiang Lihong. The study of the regularities of the rock elastic properties in Yingqiong Basin[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2001,23(4): 308-313.

[24] 史飞洲, 王彦春, 孙炜. 一种精确的纵波速度计算方法[J]. 科学技术与工程, 2017, 17(16): 7-12 Shi Feizhou, Wang Yanchun & Sun Wei. An accurate calculation method of compressional wave velocity[J]. Science Technology and Engineering, 2017, 17(16): 7-12.

[25] 陈森, 阎贫, 王彦林. 东沙群岛西南泥火山区Chirp浅剖数据的海底物性反演[J]. 地球科学, 2016, 41(3): 425-432.Chen Sen, Yan Pin & Wang Yanlin. Inversion of the physical properties of the seabed using Chirp sub-bottom data in mud volcanoes field of the southwest of Dongsha Islands[J]. Earth Science, 2016, 41(3): 425-432.

[26] 刘洁, 张建中, 孙运宝, 赵铁虎. 基于地震谱反演的地层速度估算方法及应用[J]. 石油地球物理勘探, 2016, 51(5): 909-915.Liu Jie, Zhang Jianzhong, Sun Yunbao & Zhao Tiehu. Seismic velocity estimation method based on spectral inversion[J]. Oil Geophysical Prospecting, 2016, 51(5): 909-915.