极值理论在车辆级别安全性验证中的应用及其对自动驾驶车辆的启示

为了使自动驾驶车辆可以尽可能地取代驾驶员，科学家们做了很多工作。可是如何确认自动驾驶车辆的安全性，却少有人研究。预计在极端情况下，自动驾驶车辆的安全性，是自动驾驶车辆商用化需要克服的挑战之一。

使用传统的统计方法来验证整个车辆的安全性将要求车辆覆盖所有可能发生的情况。可最近有一项研究表明，可以使用近似碰撞，并使用极值理论的方法来估计实际碰撞发生的可能性（近似碰撞的事件的频率可以用于外推，以估计碰撞的频率，这可以通过使用统计学中的极值理论来实现）。使用近似碰撞的好处是可以利用更多的可用数据来进行统计估计，这导致估计的变化较小。

为了使用这种方法，需要一个与碰撞的紧密程度有关的度量。本文表明，这种度量的选择对从数据中得出的推论有显着的影响。通过选择正确的度量，这种方法可以用于验证车辆的安全性。这在保持有效性高的同时要求的数据比现有的统计方法要低。

在本文中，使用极值理论对一个包含超过250 000公里行驶数据的大型数据集的碰撞频率进行估计。结果显示，度量的选择对从相同数据中得出的推论有很大的影响。在本文中，使用制动威胁数量（BTN）作为度量时，结果估计的可信度较高。其中BTN的计算公式如下所示：

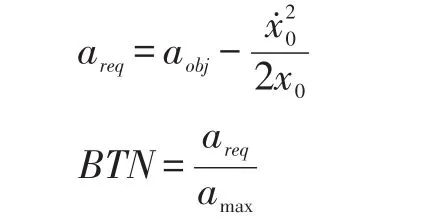
其中，[aobj]代表的是当下物体的加速度，而[areq]代表的是不发行碰撞时所需要的加速度 ，[amax]代表的是制动器所能产生的最大加速度。