基于不相似性的软件缺陷预测算法

，

(1.中国电子科学研究院，北京 100041; 2.北京自动化控制设备研究所，北京 100074)

0 引言

软件缺陷数据集中有缺陷的样本数量往往比无缺陷的样本数量少得多，因此，软件缺陷预测可被视作一个类不均衡学习问题。在类不均衡学习学习过程中，不同类别的误分代价各不相等，少数类(有缺陷)的误分代价远高于多数类(无缺陷)的误分代价，为尽可能地降低误分代价，预测算法更重视那些有缺陷的少数类样本的预测结果。然而，传统的分类算法通常建立在类分布均衡且误分代价相等的前提下，以最小化分类误差为最终目标，因此直接采用决策树分类[1-3]、神经网络[3]、贝叶斯分类[4]、支持向量机[3-6]及k-最近邻分类[1,7]等传统的机器学习算法并不能获得较好的软件缺陷预测性能。

近年来，类不均衡学习问题受到了学术界的广泛关注，机器学习和数据挖掘领域专家们在AAAI’00[8]、ICML’03[9]及ACM SIGKDD’04[10]等权威研讨会上，对类不均衡问题的本质、解决方法及其性能评估指标进行了深入地探索与研究，并从数据层和算法层两方面提出了许多行之有效的解决方法。

数据层方法，主要通过(1)抽样或生成新样本的方式，使类分布恢复均衡，如随机欠抽样[11](RUS)和随机过抽样[12](ROS)。重复抽样可以平衡类分布，但欠抽样往往会忽略某些重要样本，导致信息缺失；反之，过抽样会引入大量副本，产生冗余信息，导致过拟合。

算法层方法，侧重于改进已有分类算法或研究新的分类算法，以更好地解决类不均衡学习问题。(1)“One-Class Learning”方法[13]，该方法仅在多数类上构建分类模型，难以准确预测少数类；(2)组合学习方法，通过重复抽样构建多个分类模型、迭代更新训练样本的权重或组合多个决策树的方式，获得稳定的分类精度，如Bagging[14]、Boosting[15]及Random Forest[16]等算法。特别是，当分类模型间存在显著差异时，组合分类模型比基本分类模型更准确，但其计算量大且复杂度较高；(3)代价敏感分析，以最小化误分类代价为学习目标，如MetaCost[17]不依赖于分类算法，且可应用于任意形式的代价矩阵上，但如何确定代价矩阵目前仍然是一个难题。

学者们[18]发现：除不均衡的类分布以外，小样本、高维度及问题复杂度等因素也会影响算法性能。预测算法本质上是在挖掘数据集中属性特征与类目标概念间内在的关联关系，并建立相应的形式化预测模型。当不均衡数据集自身属性对类目标概念缺乏判别能力时，预测算法的性能将会有所下降，特别是少数类样本的预测。

现有的类不均衡学习方法侧重于如何调整类分布或改进算法，而忽略了类不均衡数据集中属性特征的判别能力。为了提升数据集属性特征的判别能力，Pekalska和Duin等人[19]提出了一种基于不相似性的表示法，用样本间不相似性替代原始属性特征，不仅保留了数据集原有统计信息，也能够获取到数据集内在的结构信息，该方法已被证实有利于预测模型的构建[20-21]。基于已有的研究成果，提出了一种基于不相似性的软件缺陷预测算法(Dissimilarity-based Software Defect Prediction Algorithm, DSDPA)，用以提升软件缺陷的预测性能。

DSDPA主要由原型选择、不相似性转换和缺陷预测三部分组成。实验过程中，采用随机选择法进行原型选择，欧几里德距离衡量样本间的不相似性，将18个软件缺陷数据集转换到不相似性空间；然后，采用最近邻分类算法(1-NN, IB1)、决策树(Decision Tree，DT)、神经网络(Multi-layer Perceptron，MLP)、朴素贝叶斯(Naive Bayes，NB)、随机森林(Random Forest，RF)和支持向量机(Support Vector Machine，SVM)6种传统机器学习算法，在基于不相似空间中的软件缺陷数据集上构建预测模型；最后，对比分析了基于不相似性的软件缺陷预测方法DSDPA的预测性能。实验结果表明，DSDPA能够有效地改善软件缺陷预测的准确性。

1 算法原理及框架

当利用机器学习算法预测软件缺陷时，预测模型的建立通常基于静态度量元的软件缺陷数据集上，而基于不相似性的软件缺陷预测算法(DSDPA)则是将原始数据集预先映射到不相似性空间，而后在不相似性空间中构建软件缺陷预测模型。DSDPA主要由原型选择、不相似性转换和分类三部分组成。图 1给出了DSDPA的基本框架，主要由基于不相似性预测模型的构建和软件缺陷预测两大环节组成。

图1 基于不相似性的软件缺陷预测算法框架

1)基于不相似性预测模型的构建。

基于不相似性的软件缺陷预测算法的构建过程主要由原型选择、不相似性转换及构建预测模型三部分组成。首先，采用原型选择方法从原始数据集中筛选出具有代表性的样本作为原型，创建原型集；然后，计算原始数据集与原型集样本间的不相似性，从而将其映射到相应的不相似性空间中；最后，利用传统分类算法在不相似性空间中构建软件缺陷预测模型。

2)软件缺陷预测。

当未知样本到来时，首先计算未知样本与原型集中各样本间的不相似性，将其映射到到不相似性空间；然后，利用已构建的软件缺陷预测模型对不相似性空间中的未知样本进行预测，即可获悉未知样本是否有缺陷。

1.1 原型选择

原型选择旨在从原始数据集中选取具有代表性的样本作为原型，作为不相似性转换时的参照。为了更好的选取原型，学者们提出了基于共享最近邻(Shared Nearest Neighbors，SNN)的 Jarvis-Patrick clustering(JPC)算法[21]、随机选择[22](RandomC，RC)、线性规划[23](LinPro)、属性选择[24](FeaSel)、模式搜索[25](ModeSeek)、基于聚类的线性规划[26](KCenters-LP)及编辑压缩(EdiCon)等方法。其中，随机选择法(RC)，即随机地从原始数据集中抽取指定数量的样本作为原型，是最简单且有效的一种原型选择方法。Pekalska等人[26,21]对比分析了上述原型方法对基于不相似性分类方法性能的影响，实验结果表明：RC和KCenters总体表现较好，但RC更便捷。

为了保证DSDPA算法的性能，选用RC作为原型选择方法，从原始软件缺陷数据集中抽取具有代表性的样本，创建原型集。假设D代表一个软件缺陷数据集，属于二类分类问题，即C={c1,c2}，Dt为训练集，D1和D2分别代表有缺陷和无缺陷类的训练集。从D抽取r个样本作为原型集合P，利用随机选择的方法分别从D1和D2中随机抽取r1和r2个样本，使原型集P={r1,r2}。

1.2 不相似性转换

不相似性转换旨在将原始数据集映射到不相似性空间，图 2给出了不相似性转换的详细过程。

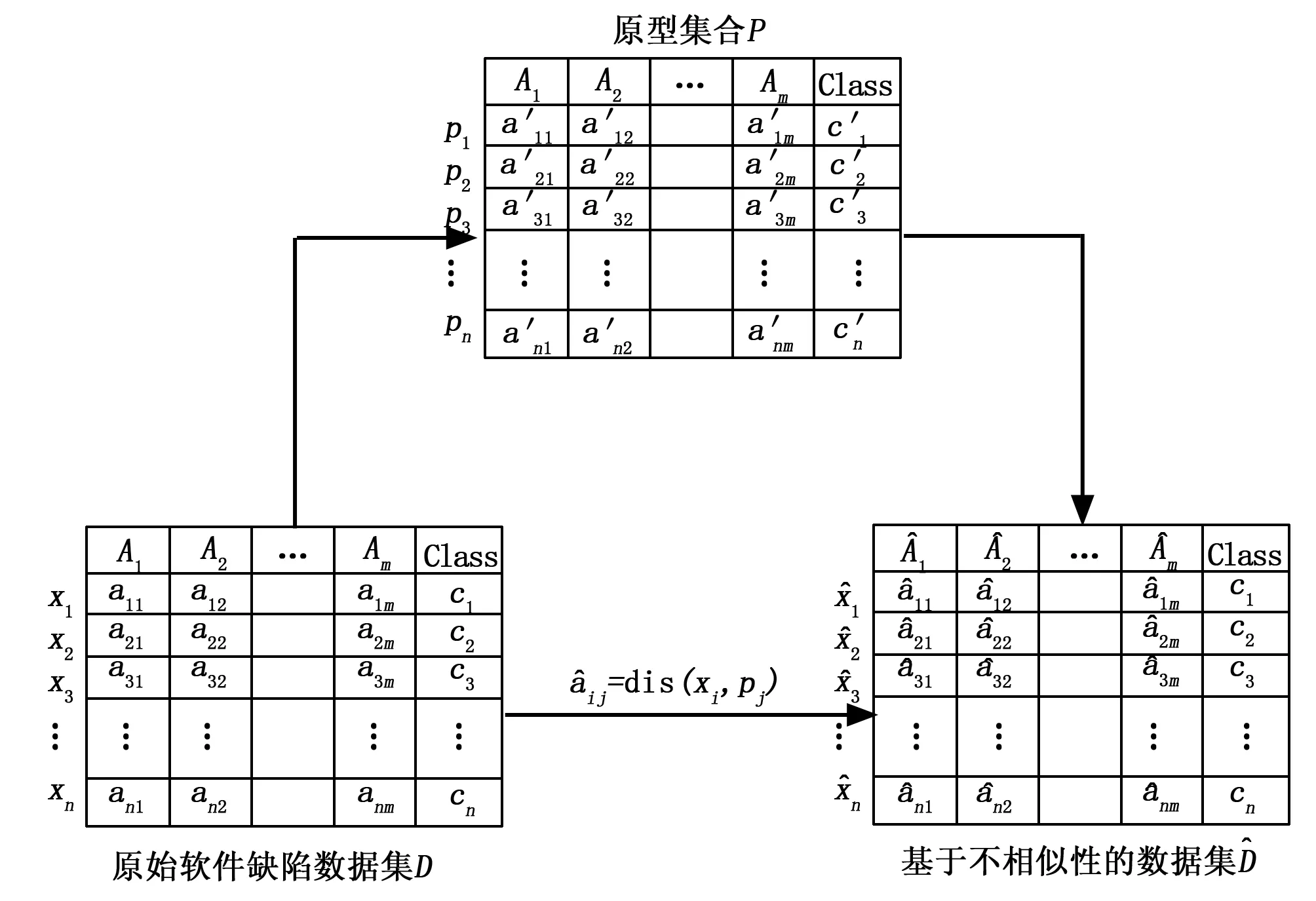
图2 不相似性转换

假设D={x1,x2,...,xn}代表样本数量为n的软件缺陷数据集。其中，xi={ai1,ai2,...,aim,ci}代表数据集D中第i个样本；xi由m个独立属性和一个类属性组成。P={p1,p2,...,pr}表示由r个具有代表性的样本构成的原型集，其中pi= {ai1′,ai2′,...,aim′,ci′} 代表第i个原型。

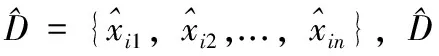
当评估密集、连续型样本间的不相似性时，基于度量的距离样本间的不相似性通常用距离度量来描述，距离越大，越不相似；反之，则越相似。目前最常用的距离度量有欧几里德距离、曼哈顿距离及闵可夫斯基距离。其中，闵可夫斯基距离是欧几里德距离和曼哈顿距离的推广，其计算方法见公式(1)：

(1)

式中，l是实数，l≥1。

当l=1时，曼哈顿距离，即L1范数；

当l=2时，欧几里德距离，即L2范数，常用于度量密集、连续的数据集中样本间的不相似性；

当l=∞时，上确界距离，又称L∞范数和切比雪夫距离，度量样本间的最大值差。

不相似性转换过程

输入：D={x1,x2,...,xn}为原始的软件缺陷数据集；

P={p1,p2,...,pr}为原型集合；

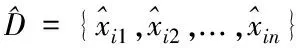
1: for eachxi∈Ddo

2: for eachpj∈Pdo

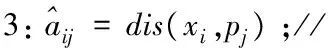
4: end

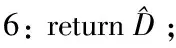
由于软件缺陷数据集中大多数属性特征是密集连续的，所以选用基于度量的欧几里德距离来度量样本间的不相似性，以实现软件缺陷数据集从原始特征空间到不相似性空间的转换。

1.3 时间复杂度分析

DSDPA算法由原型选择、不相似性转换及分类三个环节组成，其算法时间复杂度即各环节时间复杂度的总和。给定一个软件缺陷不均衡数据集D，样本数量为n，属性数量为m，利用DSDPA算法在D上进行缺陷预测时，各环节时间复杂度的计算方法如下所述：

1)原型选择的时间复杂度。

从样本数量为n的不均衡数据集中选取r个原型时，不同的原型选择方法的时间复杂也不相同。随机选择方法无放回抽样，重复r次的时间复杂度为TRC=O(r)。

2)不相似性转换的时间复杂度。

不相似性转换旨在计算原始的软件缺陷数据集与原型集中样本间的不相似性，从而将其转换到不相似性空间，不相似性转换的时间复杂度为TDT=O(n·r)。

3)缺陷预测的时间复杂度。

在样本数量为n，属性数量为r+1的基于不相似性的软件缺陷数据集上进行预测时，时间复杂度依赖于所选用的机器学习算法，TC=O(C(n,r+1))。

DSDPA算法的时间复杂度TDSDPA=TRC+TDT+TC，即TDSDPA=O(r)+O(n·r)+O(C(n,r+1))。

2 实验结果与分析

为了保证实验的客观性和可再现性，在公开的软件缺陷数据集上对DSDPA的预测性能进行了实验评估与验证。

2.1 实验数据

本实验在18来自Promise[27]数据库的软件缺陷数据集，其中5个源自PROMISE软件工程数据库，13个源自美国宇航局(NASA)MDP项目的数据集。MDP是由美国宇航局提供一个软件度量库，并通过网站提供给普通用户。MDP数据存储了系统在模块(函数/方法)级的软件产品的度量数据和相关的缺陷数据；实验数据集的样本数量分布在36～171 68之间，属性数量分布于22～41之间，不均衡率分布在1.049 2～138.21之间。表 1给出了18个软件缺陷数据集的统计信息，其中I、F、Cmin、Cmaj和 IR分别代表样本数量、属性数量、少数类样本数量(有缺陷的样本数量)、多数类样本数量(无缺陷的样本数量)以及不均衡率(Cmaj/ Cmin)。

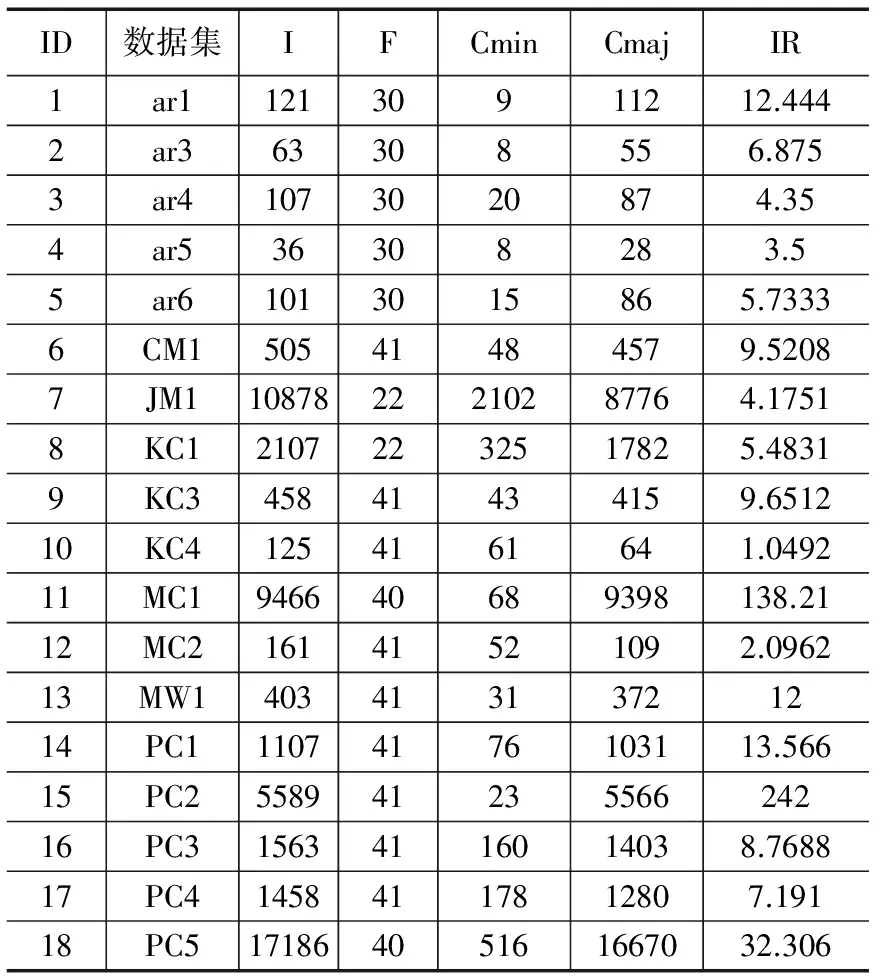
表1 18软件缺陷数据集的统计信息

2.2 实验设置

为了全面地验证基于不相似性软件缺陷预测算法(DSDPA)的有效性，并保证实验的可再现性，本节对实验中的各环节进行了如下设置：

1)软件缺陷预测算法。

不同的机器学习算法在软件缺陷数据集上的预测性能也不相同。为了考察DSDPA能否有效地改善软件缺陷数据集上的预测性能，采用了6种最常用的机器学习算法作为候选预测算法[28-29]，包括：基于实例学习的k-最近邻算法(1-NN，IB1)、决策树(J48)、神经网络(MLP)、朴素贝叶斯(NB)、随机森林(Random Forest)和支持向量机(SVM)，用以对不相似性空间中的软件缺陷数据集进行预测。

2)性能评估方法。

在评估不均衡学习方法的性能时，采用10×10折交叉验证，充分利用数据信息的同时，尽可能地减少随机序列产生的偶然误差。

3)性能评价指标。

为了评价软件缺陷预测性能，特别是有缺陷样本的预测准确率，采用AUC评估各算法在软件缺陷数据集上的预测准确性。

2.3 结果与分析

表2给出了采用DSDPA与原始数据上(Org)时，最近邻(IB1)、决策树(J48)、神经网络(MLP)、朴素贝叶斯(NB)、随机森林(RF)及支持向量机(SVM)6种机器学习方法在18个软件缺陷数据集上的预测性能AUC。由表可见，提出的DSDPA方法能够有效地改善传统机器学习方法在软件缺陷数据集上的预测性能，特别是在使用IB1和支持向量机SVM算法进行软件缺陷缺陷预测时，IB1算法在软件缺陷数据集上的分类性能平均提升了11.11%；SVM算法在软件缺陷数据集上的分类性能平均提升了12%。J48、MLP、NB算法在软件缺陷数据集上的平均分类性能也得到了提升，提升率分别为3.12%、2.5%、2.6%及2.7%。

表2算法性能比较(AUC)

3 结论

从改善软件缺陷数据集中属性特征判别能力的角度出发，提出了一种基于不相似性的软件缺陷预测算法(DSDPA)，主要由原型选择、不相似性转换及缺陷预测三部分组成。针对最近邻、决策树、神经网络、朴素贝叶斯、随机森林及支持向量机6种传统机器学习算法，对比分析了DSDPA在软件缺陷数据集上的预测性能AUC。实验结果表明：DSDPA算法能够有效地改善传统机器学习算法在软件缺陷数据集上的预测性能。

[1] Chawla NV, Japkowicz N, Kotcz A. Editorial: special issue on learning from imbalanced data sets[J]. ACM SIGKDD Explorations Newsletter, 2004, 6 (1): 1-6.

[2] Batista GE, Prati RC, Monard MC. A study of the behavior of several methods for balancing machine learning training data[J]. ACM SIGKDD Explorations Newsletter, 2004, 6 (1): 20-29.

[3] Japkowicz N, Stephen S. The class imbalance problem: A systematic study[J]. Intelligent Data Analysis, 2002, 6 (5): 429-449.

[4] Ezawa KJ, Singh M, Norton SW. Learning goal oriented Bayesian networks for telecommunications risk management[A]. International Conference on Machine Learning[C].1996: 139-147.

[5] Raskutti B, Kowalczyk A. Extreme re-balancing for SVMs: a case study[J]. ACM SIGKDD Explorations Newsletter, 2004, 6 (1): 60-69.

[6] Wu G, Chang EY. Class-boundary alignment for imbalanced dataset learning[C]. ICML 2003 workshop on learning from imbalanced data sets II, 2003: 49-56.

[7] Mani I, Zhang I. kNN approach to unbalanced data distributions: a case study involving information extraction[C]. Proceedings of Workshop on Learning from Imbalanced Datasets, 2003.

[8] Japkowicz N, others. Learning from imbalanced data sets: a comparison of various strategies[C]. AAAI workshop on learning from imbalanced data sets, 2000, 68.

[9] Japkowicz N. Class imbalances: are we focusing on the right issue[C]. Workshop on Learning from Imbalanced Data Sets II, 2003, 1723: 63.

[10] Chawla NV, Japkowicz N, Kotcz A. Editorial: special issue on learning from imbalanced data sets[J]. ACM SIGKDD Explorations Newsletter, 2004, 6 (1): 1-6.

[11] Kotsiantis SB, Pintelas PE. Mixture of expert agents for handling imbalanced data sets[J]. Annals of Mathematics, Computing & Teleinformatics, 2003, 1 (1): 46-55.

[12] Kubat M, Matwin S, others. Addressing the curse of imbalanced training sets: one-sided selection[A]. International Conference on Machine Learning[C].1997: 179-186.

[13] Manevitz LM, Yousef M. One-class SVMs for document classification[J]. The Journal of Machine Learning Research, 2002, 2: 139-154.

[14] Breiman L. Bagging predictors[J]. Machine Learning, 1996, 24 (2): 123-140.

[15] Joshi MV, Kumar V, Agarwal RC. Evaluating boosting algorithms to classify rare classes: Comparison and improvements[A]. IEEE International Conference on Data Mining[C]. 2001: 257-264.

[16] Breiman L. Random forests[J]. Machine Learning, 2001, 45 (1): 5-32.

[17] Domingos P. Metacost: A general method for making classifiers cost-sensitive[A]. Proceedings of the fifth ACM SIGKDD international conference on Knowledge discovery and data mining[C].1999: 155-164.

[18] Batista GE, Prati RC, Monard MC. A study of the behavior of several methods for balancing machine learning training data[J]. ACM SIGKDD Explorations Newsletter, 2004, 6 (1): 20-29.

[19] Pkekalska E, Duin RP. The dissimilarity representation for pattern recognition: foundations and applications[M]. World Scientific, 2005.

[20] Pkekalska E, Duin RPW. Dissimilarity representations allow for building good classifiers[J]. Pattern Recognition Letters, 2002, 23 (8): 943-956.

[21] Zhang XY, Song QB, Zhang KY, He L, Jia XL. A dissimilarity-based imbalance data classification algorithm [J]. Applied Intelligence, 2015, 42(3):544-565.

[22] Pekalska E, Paclik P, Duin RP. A generalized kernel approach to dissimilarity-based classification[J]. Journal of Machine Learning Research, 2002, 2: 175-211.

[23] Bradley PS, Mangasarian OL, Street W. Feature selection via mathematical programming[J]. Informs Journal on Computing, 1998, 10: 209-217.

[24] Jain A, Zongker D. Feature selection: Evaluation, application, and small sample performance[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19 (2): 153-158.

[25] Cheng Y. Mean shift, mode seeking, and clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1995, 17 (8): 790-799.

[26] Pekalska E, Duin RPW, Paclik P. Prototype selection for dissimilarity-based classifiers[J]. Pattern Recognition, 2006, 39 (2): 189-208.

[27] Boetticher G, Menzies T, Ostrand T. Promise repository of empirical software engineering data. Department of Computer Science[J]. West Virginia University, 2007.

[28] 马 樱. 基于机器学习的软件缺陷预测技术研究[D]. 成都. 电子科技大学，2012.

[29] 程 俊，张雪莹，李瑞贤. 基于元学习的软件缺陷预测推荐方法[J]. 中国电子科学研究院学报, 2015, 10(6): 620-627.