应用R软件的robumeta程序包实现基于鲁棒方差估计的Meta回归分析

冯雨嘉，郭梓鑫，曾宪涛，刘小平

本文是基于鲁棒方差估计的方法学介绍[1]。鲁棒方差估计（robust variance estimation，RVE）是一种处理非独立效应量的方法，由Hedges，Tipton和Johnson 提出[1]，广泛的应用于物理学，医学，生物学等方面[2,3]。在通常使用的多元Meta分析中，要求组内变异是已知的，而使用RVE方法，即使组内变异未知，也可以提供有效的标准误，点估计和可信区间[4]。

R软件拥有强大的Meta分析功能，robumeta程序包是R软件基于鲁棒方差估计实现Meta回归分析的程序包。robumeta程序包由Zachary Fisher，ElizabethTipton，HouZhipeng研发[5]，本文以Oswald等发表的文章中的oswald2013.ex1组数据（附件）为例[6]，演示该程序包的使用方法。

1 R软件及robumeta程序包的安装

本文使用R软件版本为R-3.4.1[7]，可在R语言官方网站（https://www.r-project.org/）下载最新版R软件，安装可参阅《R软件Metafor程序包在Meta分析中的应用》[8]一文。在R软件安装完毕后，双击桌面的R软件图标，即可启动R软件。于命令提示符“>”后输入命令install.packages("robumeta")，在弹出的对话框中选择某个镜像安装(CRAN)，安装完成后可由library("robumeta") 命令完成加载。至此，软件及robumeta程序包[5]已安装完毕。

2 数据加载

使用程序包自带的数据oswald2013.ex1[6]进行演示，该数据集是oswald2013数据集[6]的一个子集，oswald2013数据集包含从46个个体研究中采集的308个效应量，oswald2013.ex1数据集包含从9个个体研究中采集的32个效应量，该数据集为内隐联想测验（Implicit attitude Test，IAT）得出的数据。加载数据的指令为data(oswald2013.ex1)，具体数据参见附表1。

3 原理阐释

如前所述，本文为基于RVE方法学介绍[1]，RVE是一种处理非独立效应量的方法，由Hedges,Tipton和Johnson 提出[1]，现被广泛的运用于医学，物理学，生物学方面[2,3]。最近，Tipton等对传统的RVE进行了一些调整[9]，很好的提升了RVE在小样本中的适用性，当研究的数目小于40时，这样的调整显得尤其重要。下面将对RVE的原理进行简单的介绍。

RVE的基本原理公式[1,3]如下：

其中j=1，……，m,（研究总数为m，），T表示效应量估计，X=（X’1，……，X’m）表示设计的矩阵，ε表示残差，β表示未知的回归系数，W表示加权的分块对角矩阵，b表示用最小二乘法估计的β值。

4 数据分析

在完成数据加载之后，即可开始数据的分析。robumeta程序包的功能主要分为鲁棒方差Meta回归模型拟合，敏感性分析，绘制相应的森林图。以下将展示具体命令及相关说明。

4.1 鲁棒方差Meta回归模型拟合 鲁棒方差Meta回归模型拟合主要依靠robu()命令实现[1]robu()命令及其结果（表1）如下：data(oswald2013.ex1)

oswald_intercept<-robu(formula=effect.size～1,data=oswald2013.ex1,studynum=Study,var.eff.size=var.eff.size,rho=0.8,small = TRUE)

表1 robu()命令执行后的结果

命令中：data(oswald2013.ex1)表示加载robumeta包自带的数据oswald2013.ex1。formula可以理解为一个常规格式的线性模型，它的形式大致为y ～ x1 + x2...， y为效应量，x1 + x2...为用户指定的协变量，在intercept-only模型中，可以指定y～1，这是可选择的，不是固定的，因而，式中的effect.size ～ 1可以理解为y～1。effect.size为一列从原始数据计算得到的，用户指定的效应量。formula = effect.size～1表示选用的线性模型为effect.size～1。data = oswald2013.ex1表示使用的数据为oswald2013.ex1，studynum=Study表示选用Study列作为识别研究的特殊值。var.eff.size=var.eff.size表示用户指定的反映每个效应量组内变异的一列值。rho的缺省值为0.8，用户指定的值必须在0～1之间。small=TRUE表示使用小样本调整程序，此命令的缺省值为TURE。

4.2 敏感性分析 敏感性分析主要靠sensitivty()命令实现

sensitivty()命令及其结果（表2）如下：

sensitivity(oswald_intercept)

表2 Sensitivity()命令执行后的结果

若要对Meta回归模型进行有效的加权，则需要建立组间变异的估计值τ2，而要对τ2值进行点估计，则需要建立ρ，ρ是效应量之间常见的相关关系。灵敏性分析可用来判定ρ对τ2的效应大小。大量的研究表明，τ2值和Meta回归系数通常对ρ的变化不敏感[10]，但当组间变异明显小于组内变异时，以上结论可能不成立。

4.3 生成研究内部和研究间的协变量 生成研究内部和研究间的协变量主要靠group.mean()和group.center()命令实现

group.mean()和group.center()命令及其结果（表3～4）如下：

h i e r d a t$f o l l o w u p_m<-g r o u p.mean(hierdat$followup, hierdat$studyid)

h i e r d a t$f o l l o w u p_c<-g r o u p.center(hierdat$followup, hierdat$studyid)

命令中：hierdat$followup表示包含组均值的协变量，hierdat$studyid表示一组用于计算组均值的数据。group.mean()是用于计算组间变异的函数，group.center()是用于计算组内变异的函数。

4.4 Meta回归分析 进行完以上的数据准备之后，就可以开始进行Meta回归分析了，具体的命令和结果（表5）如下：

model_hier<-

wup_c+followup_m+binge,data=hierdat,modelw eights="HIER",studynum=studyid, var.eff.size = var,small = TRUE)

命令中：modelweights="HIER"表示选用分层效应的加权模型，另一种模型为“CORR”，表示相关效应模型。命令中其他部分所表示的含义与robu()命令中各项的含义一致。

表3 group.center()命令执行后的结果

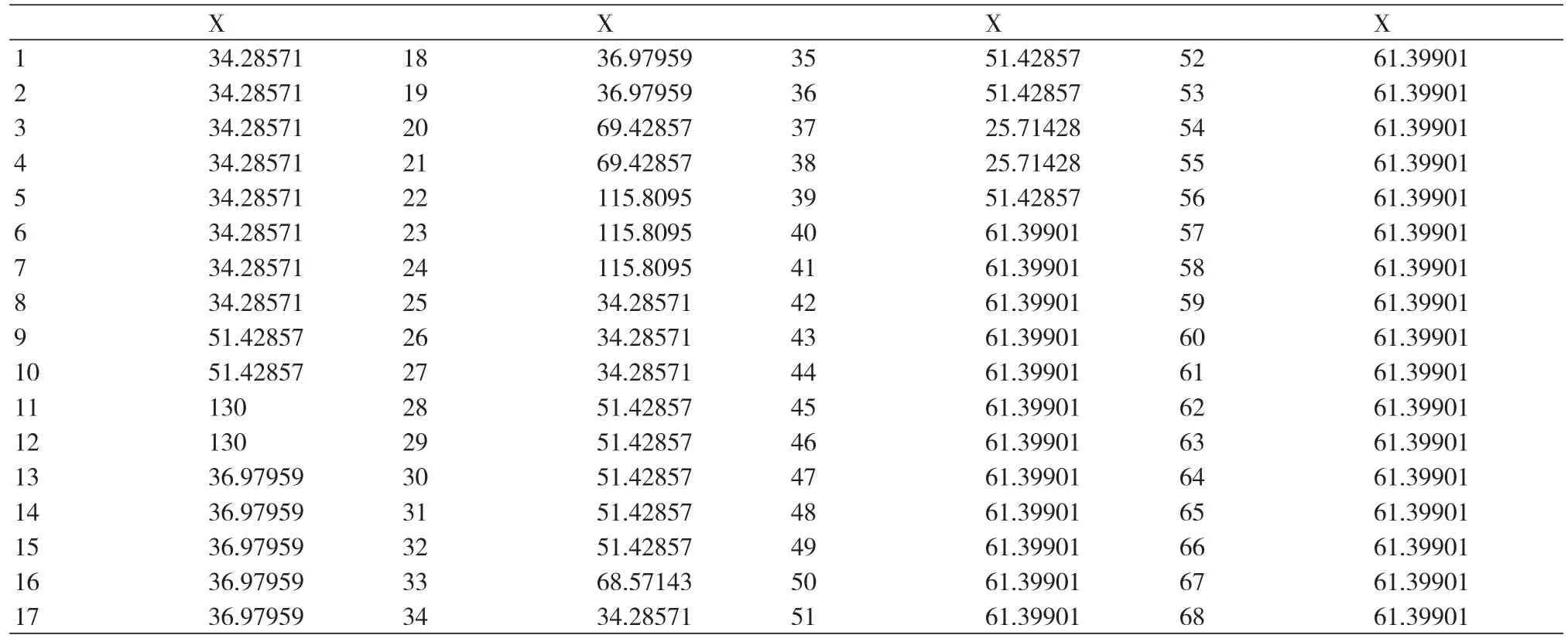
表4 group.mean()命令执行后的结果

表5 Meta回归分析的结果

4.5 输出Meta分析结果 在以上的前期计算准备完成后，就可以进行森林图的绘制了。绘制的命令如下：

forest.robu(oswald_intercept,es.lab="Crit.Cat",study.lab="Study","EffectSize"= effect.size,# optional column "Weight" = r.weights) # optional column

命令中：oswald_intercept表示使用的模型为intercept-only模型，es.lab="Crit.Cat"表示用户指定的个体效应量例如“数学分数”，“物理分数”等，这里指定的个体效应量为"Crit.Cat"。study.lab="Study"表示用户指定的一列群组效应量例如“作者姓名”，“出版年份”等，这里指定的群组效应量为"Study"。"Effect Size"= effect.size表示一列效应量，这里使用的这列效应量的名称是effect.size。"Weight" = r.weights表示使用一个名为"Weight"的RVE加权。"Effect Size"= effect.size和"Weight" = r.weights是用来阐明在命令中加入另外的列所需遵循的规则的。此命令的使用需要grid 程序包。所绘制的图形如图1。

图1 robumeta程序包绘制的森林图

5 结果汇总

在完成上述运算命令后，即可对结果进行汇总和图形的绘制。执行表6所示命令则可查看表1～表5的结果。若要将结果导出，可采用如下命令(以group.center()命令为例)：

write.csv(hierdat$followup_c,"D:/data/hierdat$followup_c.csv")

上述命令中：hierdat$followup_c表示要输出的结果的名称，"D:/data/ hierdat$followup_c.csv"表示文件导出的位置和文件名称。此命令导出的结果为csv文件，若要保存为xls或xslx格式的文件，则用excel软件打开后保存为所需格式即可。

表6 执行结果汇总的命令

6 结语

R作为当前最受欢迎的软件之一，当前国内尚无介绍robumeta程序包的文章，本文以实例对R软件robumeta程序包实现基于鲁棒方差估计的Meta回归分析的过程及结果进行了全面展示。

鲁棒方差估计提供了一种处理非独立效应量的方法[1]，但传统的鲁棒方差估计只适用于大样本的分析，而最近对传统的鲁棒方差估计进行改进后，它同时也适用于小样本的分析[9]。robumeta程序包正是基于鲁棒方差估计的原理，采用了改良的鲁棒方差估计方法，实现了利用鲁棒方差估计进行的Meta回归分析。

总之，robumeta程序包可以满足常大样本和小样本的鲁棒方差估计和Meta回归分析，且 R 的开放特性也决定了该程序包会在后期不断完善。

[1] Hedges LV,Tipton E,Johnson MC. Johnson.Robust variance estimation in meta-regression with dependent effect size estimates[J].Res Synth Methods,2010,1(1):39-65.

[2] Mente S,Kuhn M. The use of the R language for medicinal chemistry applications[J]. Curr Top Med Chem,2012,2(18):1957-64.

[3] Tipton E. Robust variance estimation in meta-regression with binary dependent effects[J]. Res Synth Methods,2013,4(2):169-87.

[4] Jackson D,Riley R,White IR. Multivariate meta-analysis:potential and promise[J]. Stat Med, 2011,30(20):2481-98.

[5] Freeman JM,Vining EP,Kossoff EH,et al. A blinded,crossover study of the efficacy of the ketogenic diet[J]. Epilepsia,2009,50(2):322-5.

[6] Oswald FL,Mitchell G,Blanton H,et al. Predicting ethnic and racial discrimination:a meta-analysis of IAT criterion studies[J]. J Pers Soc Psychol,2013,105(2):171-92.

[7] R Core Team (2015). R:A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria.URL https://www.R-project.org/.

[8] 董圣杰,曾宪涛,郭毅. R软件Metafor程序包在Meta分析中的应用[J]. 中国循证医学杂志,2012(09):1141-7.

[9] Tipton E. Small sample adjustments for robust variance estimation with meta-regression[J]. Psychol Methods,2015,20(3):375-93.

[10] Ishak KJ,Platt RW,Joseph L,et al. Impact of approximating or ignoring within-study covariances in multivariate meta-analyses[J]. Stat Med,2008,27(5):670-86.