基于局部敏感Hash的半监督直推SVM增量学习算法

，，

(浙江工业大学 信息工程学院，浙江 杭州 310023)

近年来，随着计算机网络技术和传感器技术的发展，应用软件和设备产生了大量的数据.传统机器学习大多为监督学习，被用于处理如医学[1]、交通[2]等领域中的带全部所属标签的样本.然而在现实生活应用中，大多数数据样本是无标签样本或是带少量标签的样本，而且对无标签的样本加标签是非常困难的.若要将带标签样本和无标签样本相结合进行学习，同时样本不断增加，则需要增量学习和半监督学习相结合的算法.增量学习旨在获得原训练样本与新增样本并集的最优解，而半监督学习则用于处理有标签数据和无标签数据共存的样本.由于半监督学习本身特点，被许多学者研究改进，用于许多领域，包括铁路电力系统[3]、网络应用[4]和三维模型检索[5]等.在半监督学习中，直推式支持向量机(Transductive support vector machine，TSVM)[6]

是在学习样本中包含少量标签样本和大量无标签样本中，把无标签样本中隐藏空间信息应用到最终分类器，从而提高分类器的性能和学习成本.在TSVM上，样本标注准确性影响着算法准确度方面的性能.TSVM每次迭代选取未标记样本中重要的样本进行标记，那么提高这些重要样本标记的准确性就非常重要，如文献[7]利用每次迭代中选取标记的标签准确性最高的无标记样本来提高最终分类器的分类精度；文献[8]则在惩罚参数上做文章，来控制错误标记的数量以提高性能；文献[9]为了提高准确度，利用游程计算标记样本，同时在速度方面，随着无标签样本不断增加，每次迭代的样本数量也增加，算法的训练速度就会明显下降；因此，文献[10]利用增量学习选取上次训练重要的已标记样本进行训练，避免对已标记样本全部重新训练；文献[11]在每次迭代中，用聚类的方法增加样本的数量；文献[12]用半监督聚类对未标记样本预分类.

面对带少量标签和大量无标签且不断增加的数据，上述半监督TSVM学习算法都有其局限性：1) 虽然提高了准确度或训练速度，但不具备增量学习能力，不能适应不断增长的数据；2) 如果跟增量学习相结合，其分类性能就会下降.笔者利用局部敏感Hash(Locality sensitive Hashing，LSH)思想方法，TSVM和增量学习思想相结合，提出一种基于主成分分析的局部敏感Hash的TSVM增量学习算法(Incremental TSVM with principal component analysis of locality sensitive Hashing，PCA-LSH-ITSVM).此算法利用LSH对新增无标签筛选并预标记，提高训练速度，同时也提高分类精度.实验结果表明：笔者算法能适应带少量标签和大量无标签且不断增加的数据，并有较好的性能.

1 TSVM和LSH理论基础

1.1 TSVM理论基础

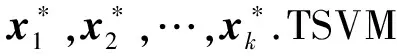
(1)

s.t.

(2)

TSVM学习训练就是获得式(1)的最优解，大致步骤为

1) 指定可调参数C，C*，利用传统的支持向量机对已标记样本进行训练，得到初始分类器.

3) 通过2)得到的样本与已标记样本一起重新做一次训练，得到新的分类器.对该分类器，利用某一规则对类别标签不同的样本标签进行交换，然后重复这一步骤，直到样本不存在符合交换规则的样本为止.

1.2 LSH理论基础

LSH算法理论基本思想：对两个在原始空间中的邻近或相似的数据样本点进行相同的映射或投影变换，得到的数据点在新空间中仍然相邻相近的概率很大，同时不相邻的数据点被映射到新空间相似的概率很小.利用一组Hash函数[13]对原空间集合中数据进行Hash投影后，就得到了一个Hash桶(即Hash表).这样就将原数据集合分到了多个Hash桶，同时这些Hash桶中的数据是相邻相似的，且该Hash桶的数据样本个数较小.因此在超大数据集中搜索相邻相似的数据样本的问题就变成了在Hash桶中的少量数据样本中搜索的问题.

Hash函数需要满足以下两个条件：

1) 如果d(x,y)≤d1，则h(x)=h(y)的概率大于等于p1.

2) 如果d(x,y)≥d2，则h(x)=h(y)的概率小于等于p2.

其中：d(x,y)为x，y之间的距离；d1，d2为距离阈值；h(x)，h(y)为x，y的Hash表；p1为满足上述条件最小的概率值；p2为满足上述条件的最大概率值.

满足上述两个条件的Hash函数则称为(d1,d2,p1,p2)Hash敏感函数.局部敏感Hash：指利用一个或者多个(d1,d2,p1,p2)的敏感Hash函数对原始样本数据集进行Hash映射，生成Hash表的过程.而局部敏感Hash函数族有多种，如汉明距离下的最小Hash函数族[14]、欧氏距离下的基于p-稳定分布的Hash函数族[15]等.它们是根据不同距离量度进行划分的.

2 基于PCA-LSH的半监督ITSVM增量学习

2.1 PCA-LSH的构建

利用主成分分析(Principal component analysis，PCA)投影得到的特征向量进行Hash编码投影，而不是随机的向量.这种特征子空间提供了很好的近似输入空间，逼近误差可以通过累积输入特征成分的近似子空间占整个输入空间的比率来控制.因此，通过PCA来替代LSH投影的随机向量，可以很容易从一个给定的数据分布来确定一个合适的Hash函数数量.

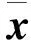
(3)

设Hash编码的一维空间向量区域为[1,P]，F(vi)为Hash函数，则1≤F(vi)≤P.P为Hash值向量每一维所能取得的最大值，即F(vi)为

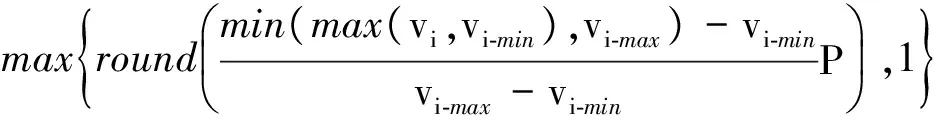
(4)

式中：vi-min，vi-max分别为初始输入样本投影后特征向量的第i个特征值的最小值和最大值；round()为四舍五入函数.

因此，输入特征向量的Hash值向量h(x)为

h(x)={F(v1),F(v2),…,F(vi)}

(5)

然后利用h(x)组成Hash表H为

H=[h(x1),h(x2),…,h(xn)]

(6)

最后利用h(x)，H对新增样本进行筛选.

2.2 基于PCA-LSH的ITSVM学习算法

将有标签样本进行LSH后，每个样本会得到一个Hash值向量，那么Hash值向量的标签为这个样本的标签.同时LSH具有搜索近邻和相似的数据样本特点.因此可以在利用LSH对新增无标签进行筛选的同时，利用Hash值向量对应的标签对筛选的样本进行标记.结合LSH快速搜索查询和能标记的特点，提出了一种基于PCA-LSH的ITSVM半监督增量学习算法PCA-LSH-ITSVM，其在提高训练学习速度的同时，也提升了精度.

假设少量的有标签样本集为Ω0，第一次新增无标签样本集为Ω1，第二次新增无标签样本集为Ω2，第一次TSVM增量学习后得到的SV集为Ω1SV，少量的有标签样本集为Ω0，进行PCA-LSH后的Hash表为H0，第一次TSVM增量学习后得到的SV集LSH后Hash表H1，更新后的Hash表为H，第一次新增的每个样本PCA-LSH后的Hash值向量为h(Ω1)，第一次新增样本筛选后的样本为Ω1LSH，第二次新增的每个样本PCA-LSH后的Hash值向量为h(Ω2)，第二次新增样本筛选后的样本为Ω2LSH，f(x)=ω·x+b为TSVM的决策函数.以上SV(Support vector)为支持向量.则PCA-LSH-ISVM算法的详细描述如下：

1) 首先将Ω0通过PCA-LSH建立Hash表H0，其中每个Hash值向量带标签，同时将Ω1每个样本通过PCA-LSH得到Hash值向量为h(Ω1).

2) 筛选和初始标记新增无标签样本集Ω1：如果Ω1中样本对应的h(Ω1)落在H0中，则筛选出样本并利用H0的标记进行初始标注，最后得到筛选后的样本集Ω1LSH.

3) 将Ω0，Ω1LSH作为TSVM学习的训练集，训练得到决策函数f(x).

4) 利用f(x)对筛选后的Ω1LSH重新标记，将标记后的结果与上次(初始)标记结果相比较.若存在不相同，则将该样本设为无标记样本(标记为0)但样本还在Ω1LSH中，再将Ω0，Ω1LSH作为TSVM学习的训练集，训练得到新的决策函数f(x).否则结束本次增量TSVM学习，得到SV集为Ω1SV.

5) 利用f(x)对筛选后的Ω1LSH重新标记，将标记后的结果与上次标记结果相比较.若存在不相同，但不是无标签(标记为0)样本，则将该样本设为无标记(标记为0)样本，同时将之前无标记的样本设置为这次的标记，它们仍然在Ω1LSH.

6) 再将Ω0，Ω1LSH作为TSVM学习的训练集，重复步骤5)，直到两次标记结果相同.结束本次增量TSVM学习，得到SV集为Ω1SV.

7) 将Ω1SV通过PCA-LSH建立Hash表H1，其中每个Hash值向量带标签，同时将Ω2每个样本通过PCA-LSH得到Hash值向量为h(Ω1).再对Ω2进行筛选和初始标记，得到Ω2LSH.再将Ω1SV，Ω2LSH合并，样本集为Ω2LSH.

8) 将Ω0，Ω2LSH作为TSVM学习的训练集，训练得到决策函数f(x).重复步骤4)～6)(将其中的Ω1LSH改为Ω2LSH即可)，得到新的SV.

9) 下一个新增样本重复步骤7)，8)，直到没有新增样本.得到最终决策函数.

3 实 验

为了验证算法的性能，对比了笔者提出的PCA-LSH-ISVM算法与传统TSVM算法、一般增量TSVM算法的精度和训练速度性能.其中ITSVM是指将上次TSVM学习训练得到的SV，本来有标签的样本与增量无标签样本进行TSVM学习训练.实验在i5 M430处理器上进行，主频为2.27 GHz，内存为4 GB，软件为PyCharm 5.0.3.

为了验证算法的性能，将PCA-LSH-ITSVM，TSVM，ITSVM算法作对比.实验在UCI标准数据集Steel，Magic，Default of credit card clients(Credit)分别进行：1) 实验随机从以上3 个数据集中随机选取600 个样本，其中一半为训练样本，一半为测试样本；2) 训练样本去除部分标签，以有标签样本集数量占总数的5%，10%，15%，20%的比例进行实验；3) 在增量学习上，训练样本分成初始样本集(其为有标签样本)和5 个无标签的增量样本集.数据集个数、特征个数如表1所示.

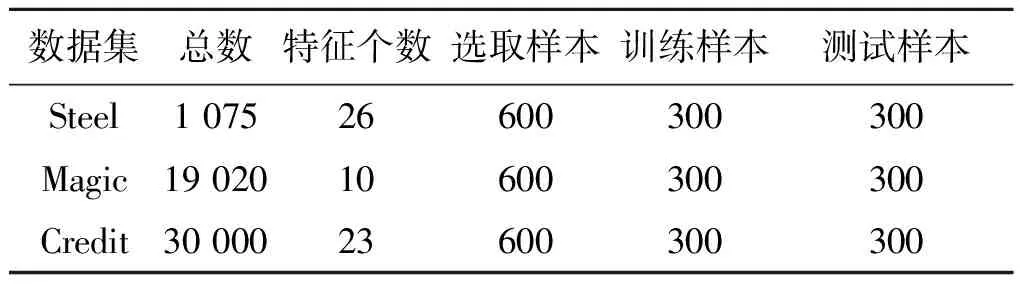
表1 数据集Table 1 The data set 个

3.1 实验分类精度结果及分析

在Hash函数参数P=8的情况下，对比各算法的分类性能.其中PCA-LSH只是对新增样本进行筛选和初始标记，并不改变样本的原来属性(未进行其他预处理)，这样保证与其他算法训练学习的对象样本一致性.实验结果如表2～4所示.

表2不同算法在Steel中分类精度

Table2TheclassificationaccuracyofdifferentalgorithmsinSteel%

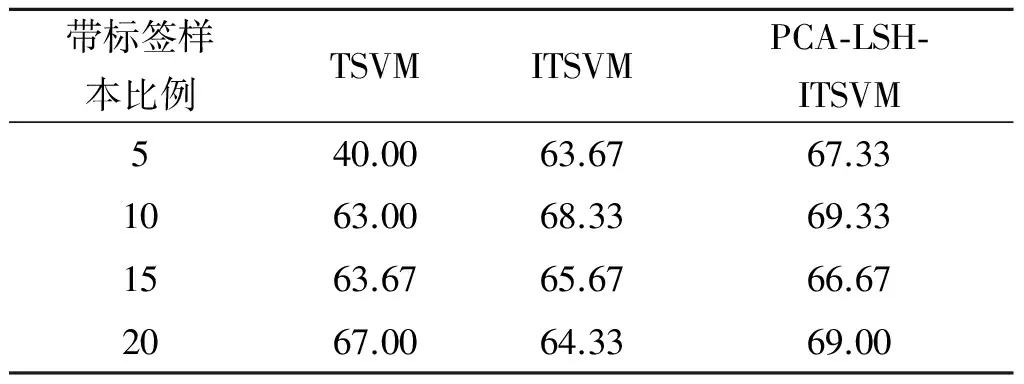
表3不同算法在Magic中分类精度

Table3TheclassificationaccuracyofdifferentalgorithmsinMagic%

表4不同算法在Credit中分类精度

Table4TheclassificationaccuracyofdifferentalgorithmsinCredit%

由上述实验结果可知：

1) 当训练样本中初始带标签样本数量较多(比例为20%)时，由于带标签样本能较好地代表整体样本集(其含有较多的分类信息)，因此三者算法的精度相近，但笔者提出的PCA-LSH-ITSVM算法精度最高，比传统TSVM算法平均高2%左右.

2) 当训练样本中初始带标签样本数量较少(比例为5%)时，由于带标签样本不能较好地反应整体的分类信息，算法TSVM，ITSVM分类性能很差，但笔者算法能有效地利用少量的带标签样本筛选并标记无标签样本使第一次训练的样本能较好反应出整体分布，从而提高分类性能，笔者算法分类精度比TSVM算法高了20%左右.

3) 随着有标签样本比例的升高，其分布信息能更好地反应整体样本，因此各算法的性能也在升高.

总之，笔者算法利用PCA-LSH较准确地给无标签样本进行初始标记，避免了设定TSVM中初始正标签样本数对精度影响；同时在第一次训练前，先利用PCA-LSH和有标签的少量样本对第一次增量无标签样本进行筛选标记(相当于是第一训练样本能更好地反应整体样本)，使得第一次获得SV集准确.因此，在有标签样本数量很少时，笔者算法保持良好的分类性能，而其他算法则性能较差；在有标签样本数量多时，笔者算法比其他算法有更高的分类精度.

3.2 实验训练速度结果及分析

在Hash函数参数P=8的情况下，对比各算法的分类性能.在训练样本总数为300个时，算法在不同带标签样本比例下的速度，实验结果如表5～7所示.

表5 不同算法在Steel中训练速度Table 5 The training speed of different algorithms in Steel

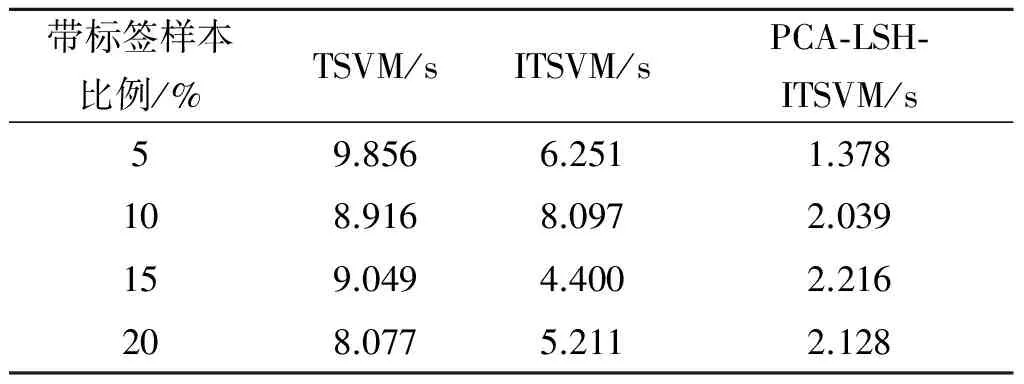
表6 不同算法在Magic中训练速度Table 6 The training speed of different algorithms in Magic

表7 不同算法在Credit中训练速度Table 7 The training speed of different algorithms in Credit

由上述实验结果可知：

1) 在实验有标签样本的比例下，笔者算法的训练速度都优于TSVM，ITSVM.当训练样本中初始带标签样本比例越小时，笔者算法的速度优势越明显.

2) TSVM，ITSVM的训练速度随着带标签样本比例的增加，会有加快的趋势.其中ITSVM大部分速度都优于TSVM，因为ITSVM就是增量学习，减少部分标记样本的迭代次数.

3) 笔者算法的速度快且平稳.其速度在不同标记样本比重都是最优.因为笔者算法利用增量学习减少部分标记样本的迭代次数的同时，还利用PCA-LSH对增量样本进行筛选，减少训练样本的数量，减少迭代.

总之，笔者算法利用PCA-LSH对增量样本进行筛选，而且增量学习使得训练速度明显加快.因此当初始标签样本数量很少时，相对其他两种算法，笔者算法训练速度有明显优势；在有标签样本数量多时，其他两种算法训练速度加快，但笔者算法的训练速度还是有较大的优势.

4 结 论

为了提高机器学习在大数据集中的半监督学习性能，基于局部敏感Hash和增量学习提出了一种基于主成分分析的局部敏感Hash的SVM快速增量学习算法PCA-LSH-ITSVM.该算法利用主成分分析与局部敏感Hash相结合的PCA-LSH对新增无标签样本进行筛选和标记，避免了设定TSVM中初始正标签样本数对精度的影响，提高分类精度，同时由于是增量学习和对数据集筛选，减少了TSVM迭代次数，双重加快了训练速度.实验结果表明：在少量带标签和大量无标签的数据中，该算法相对传统TSVM和一般的TSVM在分类精度和训练速度有其明显优势，尤其在带标签样本数量很少时.

[1] 龙胜春，尧丽君.行程长度纹理特征应用于肠癌病理图片识别[J].浙江工业大学学报，2015，43(1)：110-114.

[2] 邵奇可，李路，周宇，等.一种基于滑动窗口优化算法的行人检测算法[J].浙江工业大学学报，2015，43(2)：212-216..

[3] 刘子军.基于TSVM的铁路电力系统谐波检测方法研究[M].重庆：重庆大学，2015.

[4] 李斌，李丽娟.基于改进TSVM的未知网络应用识别算法[J].电子技术应用，2016，42(9)：95-98.

[5] 徐彩虹，刘志，潘翔，等.一种基于实例学习的三维模型检测匹配方法[J].浙江工业大学学报，2012，40(3)：326-330.

[6] JOACHIMS T. Transdutive inference for text classicication using support vector machines[C]//International Conference on Machine Learning. San Francisco: Morgan Kaufman, 1999: 200-2009.

[7] 陈毅松，汪国平，董士海.基于支持向量机的渐进直推式分类学习算法[J].软件学报，2003，14(3)：451-460.

[8] 王安娜，李云路，赵锋云，等.一种新的半监督直推式支持向量机分类算法[J].仪器仪表学报，2011，32(7)：1546-1550.

[9] 廖东平，魏玺章，黎湘，等.一种改进的渐进直推式支持向量机分类学习算法[J].信号处理，2008，24(2)：213-218.

[10] 彭新俊，王翼飞.双模糊渐进直推式支持向量机算法[J].模式识别与人工智能，2009，22(4)：560-566.

[11] 薛贞霞，刘三阳，刘万里.改进的直推式支持向量机算法[J].系统工程理论与实践，2009，29(5)：142-148.

[12] 王立梅，李金凤，岳琪.基于k均值聚类的直推式支持向量机学习算法[J].计算机工程与应用，2013，49(14)：144-146.

[13] ANDONI A, INDYK P, NGUYEN H L. Beyond locality-sensitive Hashing[C]//Proceedings of the Twenty-fifth Annual ACM-SIAM Symposium on Discrete Algorithms. New York: ACM, 2014: 1018-1028.

[14] GIONIS A, INDYK P, MOTWANI R. Similarity search in high dimensions via Hashing[J]. Peer-to-peer networking and application, 2000, 8(2): 216-228.

[15] DATAR M, IMMORLICA N, INDYK P, et al. Locality sensitive Hashing scheme based on p-stable distributions[C]//Proceedings of the Twentieth Annual Symposium on Computational Geometry. New York: ACM, 2004: 23-36.