基于美国标准的轨道交通车辆不锈钢车体屈曲分析

刘春艳　胡　季

（中车长春轨道客车股份有限公司工程实验室，130062，长春∥第一作者，高级工程师）

随着中国轨道交通车辆技术的发展，走向国际市场已成必然趋势。目前，我国城市轨道交通车辆已在美国市场崭露头角，并取得了喜人的成绩。但美国严格的产品验收标准，对于我国车辆制造企业来说是一个非常大的挑战。因为美国用户对车体强度要求非常高，故各大供应制造商一般会选用屈服强度较高的不锈钢材料作为制造车体钢结构的原材料（我国国内以冷轧不锈钢板材居多）。轨道交通车辆的车体结构一般由长大的薄板与梁构成，由于冷轧不锈钢材料成分的特点，车体结构较易发生屈曲而导致结构失稳。

结构稳定性可以理解为结构在外界干扰之下的自我控制能力。结构中的杆、梁、板，或者由它们组成的结构，之所以有可能发生屈曲或失稳，其主要原因是作用在其中的广义膜力引起的膜应变能有可能被转换成弯曲应变能。例如：一个受压的细长杆，当压力达到一定值时，加上一极小的横向载荷就可能产生很大的横向挠度，且横向挠度随着压力的增大而急剧增大，从而导致结构完全失效。其实，这个过程就是杆受压获得膜应变能转变成弯曲应变能的过程。

如何采用仿真分析手段，有效地验证结构的屈曲问题，这一点在稳定性分析中至关重要。本文以某城市轨道交通车辆的不锈钢车体钢结构为例，基于美国相关标准与文献，论述车体钢结构的屈曲分析过程。

1　车体有限元模型

车辆的车体结构中，外侧由长大薄板构成，内侧则根据载荷的传递布置横向、纵向的加强梁，并通过较强的上、下边梁和端角柱形成车体的框架结构。结合车体结构特点，车体的有限元模型均采用了板壳单元进行模拟，对关键部位和主要传递力的结构进行了网格细化（见图1）。

图1　车体有限元模型

根据美国标准SEI/ASCE 8-02《Specification for the Design of Cold-Formed Stainless Steel Structural Member》中所述，冷轧不锈钢材料具有很高的各向异性，受压能力远小于受拉能力。该标准中的表A1给出了不锈钢不同牌号的不同方向的屈服应力值。结合我国的不锈钢生产工艺，表1给出了得到用户认可的并已应用于所研究车辆的不锈钢材料拉伸和压缩屈服应力值。

该车体结构要求在端梁处施加1 424 kN的力，整个结构的屈曲因子应超过1.562 5。同时，需要对超过材料压缩屈服强度35%的部位进行重点分析。

表1　车体不锈钢材料特性参数

2　有限元分析计算

2.1　整车变形

2.1.1边界条件

因车体左右完全对称，为了提高计算效率，特选用半车作为分析对象（如图2所示）。施加在一位端端梁上的纵向载荷F=（1 424 kN/2）×1.562 5=1 112.5 kN；另一端的端梁采取纵向约束，并在车体中心面上施加对称约束，在空气弹簧处采取垂向约束。同时采用材料的纵向压缩屈曲强度对有限元模型进行非线性设置，作为有限元模型屈曲分析的一部分。

图2　半车有限元模型边界示意图

2.1.2分析结果

将设置好的有限元模型进行求解分析，并查看整车各向的整体变形。在变形比例放大到5倍的状态下，并没有发现整车位移突变的情况（见图3）。

同时对不同载荷下的受力和位移进行对比，得出整车位移与力的关系。由图4可知，整车在受力变化情况下，位移与受力成线性关系，表明整车并没有发生失稳现象。

图3　车体整体变形位移云图

图4　位移-力关系曲线图

2.2　局部分析

2.2.1薄板分析

针对“超过材料压缩屈服强度35%的部位进行分析”这一要求，采用整车有限元模型进行局部静强度线性分析。其边界条件如图5所示。

首先通过计算结果的判断，发现在中梁局部部分压应力超出了材料压缩屈服应力的35%（如图6所示），故对该处进行分析。

因为该板在宽度方向上的各个节点所受的压应力较为一致（σmax=210 MPa），根据文献［2］第 2部分“Design，Fabrication，and Construction of Freight Cars”第4章的描述，选取“Rectangular plate under equal uniform compression on two opposite edges”作为该结构的评价类型，其屈曲分析选取判定公式为：

图5　整车有限元模型边界示意图

图6　中梁下盖板处应力云图

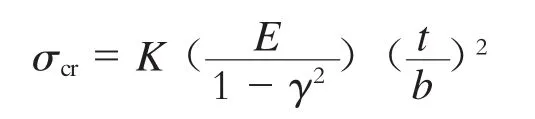
式中：

K——与分析对象的约束条件和几何尺寸有关的参数（见表2）；

E——材料杨氏模量，取186 000 MPa；

γ——泊松比，不锈钢材料取0.3；

t——板材的厚度，取4 mm；

b——分析对象的宽度，取214 mm；

σcr——结构的稳定许用应力。

当板材的长度a=400 mm时，根据分析对象的信息可得

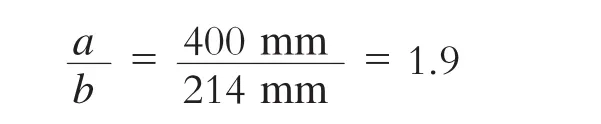
结合表2，K值取3.29，可得

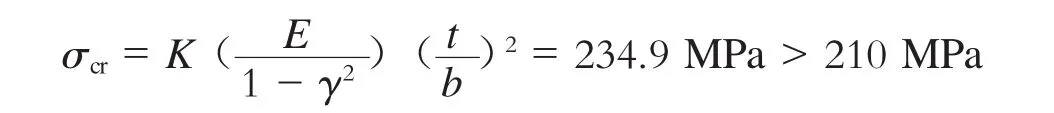
根据计算结果可知，该结构满足技术合同中规定的屈曲要求。

2.2.2短梁分析

根据有限元分析可发现压溃箱处所承受的压应力（σmax=287 MPa）超出材料压缩屈服应力的35%（如图7所示），故对该处进行分析。

结合压溃箱的几何外形，可得

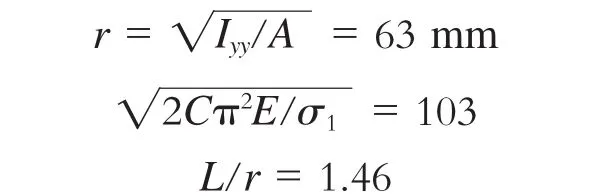
式中：

Iyy——压溃箱最小截面惯性矩，取18 715 813 mm4；

A——截面积，取4 716 mm2。

C——压溃箱两端连接方式因子，取1；

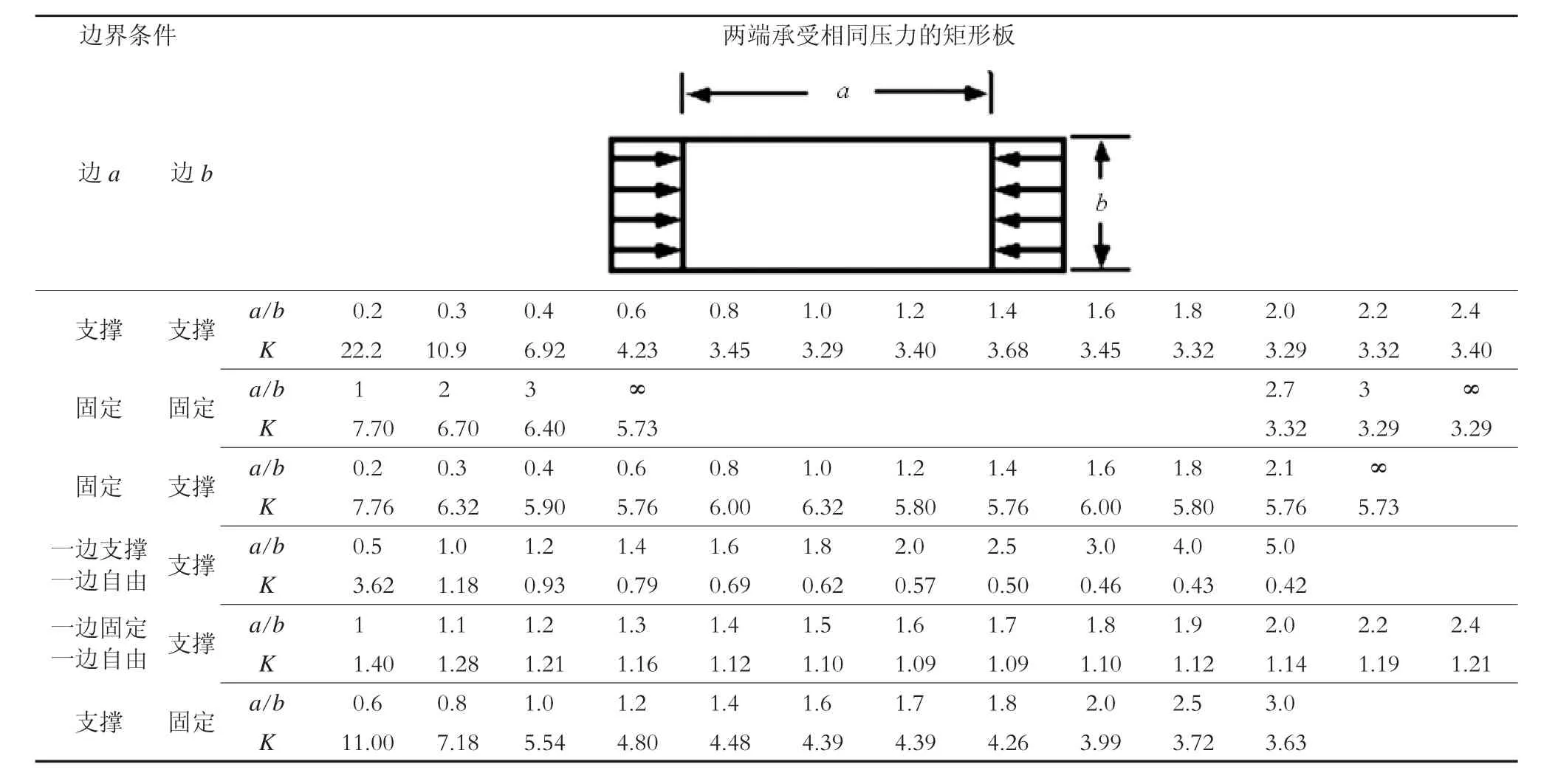
表2　车体薄板屈服分析参数表

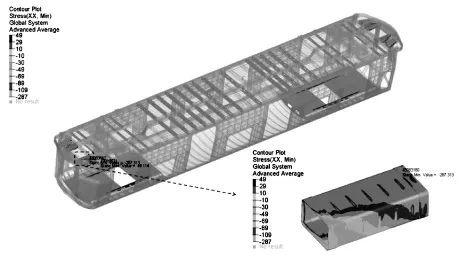
图7　压溃箱应力云图

σ1——压溃箱材料的压缩许用极限，310 MPa。

L——分析对象长度，取92 mm。

进行评估。根据所选的分析对象的信息可得

根据以上计算结果，可知该处满足屈曲要求。

3　结论

（1）对整车在1 424 kN端梁压缩力的作用下，整车变形和局部屈曲的分析结果表明，该车体结构满足技术合同所规定的屈曲分析要求。

（2）车体静强度试验表明，在1 424 kN端梁压缩力的作用下，目测整车各处并没有产生屈曲现象。

（3）屈曲分析是车体结构，特别是不锈钢材料车体结构的重要考核指标之一，而有限元分析方法是目前校核车体结构屈曲最有效的手段。今后应加强轨道车辆屈曲试验方法的研究，用于验证设计结构在稳定性方面的合理性。

［1］美国土木工程师协会.Specification for the Design of Cold-Formed Stainless Steel Structural Members：SEI/ASCE 8-02［S］.Reston：美国土木工程师协会，2002．

［2］美国铁路协会.Manual of Standards and Recommended Practices Section C：Part II［S］.华盛顿：美国铁路协会，2007．

［3］刘鸿文．材料力学［M］．4版.北京：高等教育出版社，2004．

［4］严隽耄．车辆工程［M］．北京：中国铁道出版社，1999.

［5］姚亚涛，肖守讷，朱涛.速度200 km/h客车不锈钢车体结构稳定性分析［J］．铁道机车车辆，2016，36（6）：5.

［6］丁彦闯，兆文忠，马思群，等.屈曲分析在车辆应用中的关键技术［J］．大连铁道学院学报，2003，24（2）：5.