基于极限学习机的锂电池健康状态预测

陈 婕，金 馨

（南京市第三高级中学，江苏 南京 210001）

0 引言

目前随着相关科技技术的发展和对环境能源保护的需求，蓄电池系统的有效管理日益重要。由于设备通常都会有极高的综合性和复杂性，对设备的可靠检测及预测可以解决当前不能及时发现设备故障而引发的经济、安全问题。对系统中的电池状态进行监测，有效地对蓄电池的剩余寿命进行预测，能够有效地保护实时电池系统[1-2]。在本文中，采用蓄电池的健康状态（State of Health，SOH）探讨锂电池剩余寿命，有着重要的研究意义[3]。

传统的电池研究方法主要基于电池可直接测量到的参数，如电压、电流、温度、内阻等，常见方法有电池充放电研究、化学方法或者电压、电流测量的方法[4-5]，这类方法有长时、昂贵且阻碍电池主要性能等缺点，且传统预测方法针对性强、考虑因素单一、预测精度有待改进且适用范围比较小。由于蓄电池内部具有复杂结构并存在化学反应，单纯地使用一两个参数或线性测量的方法不能够很好地预测SOH，准确性有限。人工智能方法因其强大的适应性，近年来被研究应用于蓄电池SOH的预测，常用的人工智能算法主要有：卡尔曼滤波（Kalman Filter，KF）法、人工神经网络（Artificial Neural Network，ANN）算法[6-7]、RVM算法[8]、遗传算法[9]、自组织网络[10-12]、模糊推理算法[3]以及这些算法互相结合的方法等等。

本文主要研究基于极限学习机的蓄电池剩余寿命的预测[1,2,7]。通过不同方法的比对，希望找到效率高、性能好的蓄电池剩余寿命预测模型，实验结果也验证极限学习机的效率和性能要优于部分神经网络算法，能够改善反向传播网络学习速率慢、设置参数多及容易发生欠拟合和过拟合现象的问题。

1 极限学习机

极限学习机（Extreme Learning Machine，ELM）是黄广斌在2004年提出的新型快速学习算法，如图1所示。相较于传统的神经网络，ELM是一种简单易用、有效的单隐层前馈神经网络学习算法[13]，用于解决传统神经网络算法容易产生局部最优解、迭代次数过多和学习速率慢等问题。传统神经网络算法在训练过程中往往需要大量时间设置多种参数，并且参数的选取对实验的最终结果会产生较大影响，其收敛速度也会被波及，也容易发生过拟合和欠拟合现象，比较而言，ELM算法在多层面表现出优越性。

图1 极限学习机模型Fig.1 Extreme learning model

ELM 是一种单隐层前馈型神经网络（Single hidden Layer Feed-forward Network，SLFN），随机选择输入权重和隐含层偏置。一个单隐层神经网络，设输入层节点数为n，输出层节点数为m，隐含层节点数为l，输入层节点数即为数据样本的输入特征数，则对于给出的N个样本的输入xi(i = 1 ,2,…,N)可以表示为： xi=[xi1xi2… xin]，对应的全部样本的输入特征向量X可表示为：

上式中的行向量即对应数据集中所有样本的输入向量 xi。

对于给出的N个样本的输入yi(i = 1 , 2, … , N)可以表示为： yi=[yi1yi2… yim]，对应的全部样本的输入特征向量Y可表示为：

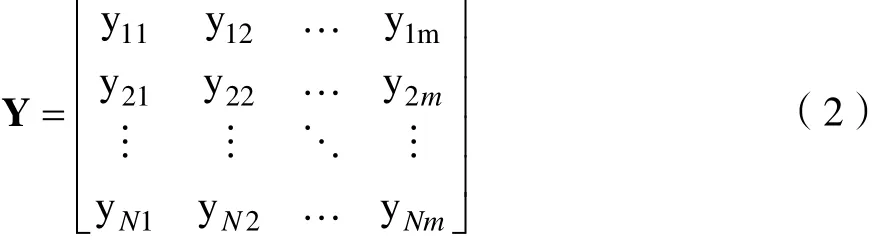
上式中的行向量即对应数据集中所有样本的输出向量 yi。

N个样本（ xi, yi），设定隐含层节点数为l时，极限学习机模型可以表示为：

其中，g(x)为激励函数， xi为输入向量， ωj=[ω ω … ω ]T是第j个隐含层元和各输入层间的

1 j 2j nj输入权重向量， bj为第 j层隐含层元的偏置， βj=[β β … β ]T是第j层隐含层元与输出层间的j1 j2 j m权重向量， ωj⋅ xi表示 ωj和xi的内积。公式（3）可改写简化为：

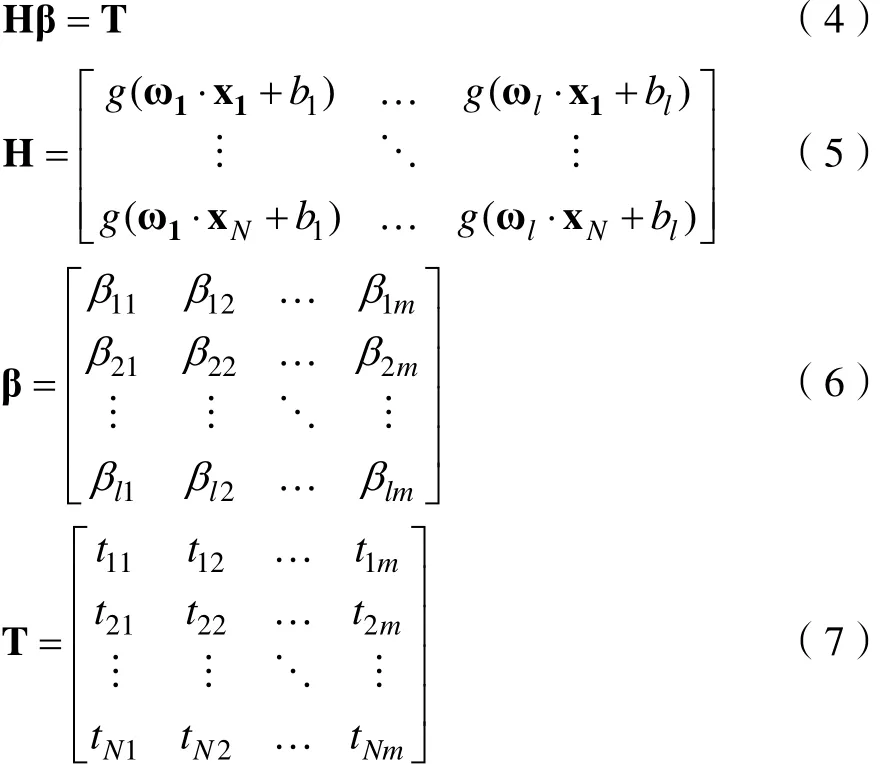
H的维度为Nl×，β维度为lm×，T维度为Nm×。

此类的神经网络模型的学习目标是使得利用训练模型得出的样本估计值同样本的实际输出的误差最小，可表示为：

其中，iy为第i个样本的实际输出，it为第i个样本的预测输出，我们希望样本的预测输出同其实际输出间的误差尽可能的小。可以通过传统的基于梯度下降算法求解权重和偏置值的估计值，在ELM算法中，输出权重可由被随机确定的输入权重和偏置值求解得出，它的解的范数是最小且唯一的。实验过程中，设置初始值后，通过足够的迭代求取使得预测值同实际值误差均方根最小的权重值和偏置值的解。

2 实验结果及分析

2.1 数据集

实验的数据来自于NASA的蓄电池测试数据[14]，一组四种不同类型的锂离子电池（5号、6号、7号和18号）在室温下以3种不同的操作模式（充电、放电、阻抗）进行数据测试。充电是在恒定电流（CC）模式下以1.5 A进行充电直到电池电压达到4.2 V，然后继续在恒定电压（CV）模式进行，直到充电电流下降到 20 mA。放电是在恒定电流（CC）2 A水平下进行直到5号、6号、7号和18号电池的电压分别下降到2.7 V、2.5 V、2.2 V和2.5 V。阻抗测量是通过电化学阻抗谱（EIS）从0.1 Hz～5 kHz进行频率扫描，重复充电和放电循环导致电池加速老化，其提供了深入了解内部电池参数随着老化的进展而变化的信息。实验停止时，电池达到寿命终止（EOL）标准，额定容量衰减 30%（从 2 ahr到1.4 ahr）。此数据集可用于对一个给定的放电周期的剩余电量和剩余寿命（RUL）预测，数据集中给出了三种操作类型：充电、放电或阻抗，以及三种模式下的温度、时间、测量电压和测量电流。

对NASA蓄电池实验数据进行特征抽取，原始数据给出若干充电、放电和阻抗模式下的测试数据，将原始数据直接用于实验将会使得实验数据维度过于庞大且信息量过多。因此需要对原始数据进行数据处理，将处理后的分别包含168个（5号、6号、7号电池）或132个6维样本数据运用于后续模型训练。

2.2 预测模型建立过程

利用从原始数据集中抽取的特征，建立5输入（电池的平均温度T、电池的平均电压V1、负载的平均电压V2，电池的电解质电阻Re和电池的电荷转移电阻 Rct）、1输出（蓄电池剩余寿命）的蓄电池 BP神经网络模型和极限学习机模型。在MATLAB中建立BP神经网络模型、极限学习机和核函数极限学习机，其主要步骤可分为：

（1）对原始数据集进行特征抽取，并进行标准化；

（2）将标准化后的数据划分为训练集和测试集，实验中将前100个数据划分为训练集，剩余数据作为测试集；

（3）设置 BP神经网络模型的若干参数，如迭代次数、学习速率和目标值等；设置极限学习机的类型参数，0为回归模型，1为分类模型，蓄电池剩余寿命预测是回归问题，设置参数值为0；

（4）进行网络模型的训练，寻找合适的隐含层节点参数和激励函数，核极限学习机模型则需寻找合适的核函数，实验采用RBF核还需寻找正则项系数C和核参数P；

（5）模型训练结束，记录寻找到的适宜的隐含层节点参数值，以及寻参结果下的RMSE和测试集预测输出，用于后续方法比对和实验结果绘图。

实验过程中，带核的极限学习机模型只要确定核函数的种类和核函数的参数，其输出即为确定值，但 BP神经网络模型和极限学习机模型都存在输出随机性的问题。为减免这两种模型寻参过程中随机输出对最终预测结果的影响，采取多次实验取均值的方法判定其预测性能。

2.3 实验结果与分析

在模型训练过程中，分别对处理过后的 NASA数据集使用BP神经网络、极限学习机ELM和核极限学习机 ELM_kernel等方法，采用均方根误差（Root Mean Square Error，RMSE）和计算时间（Time，T）对模型的性能进行评估，其中均方根误差RMSE的定义如下：

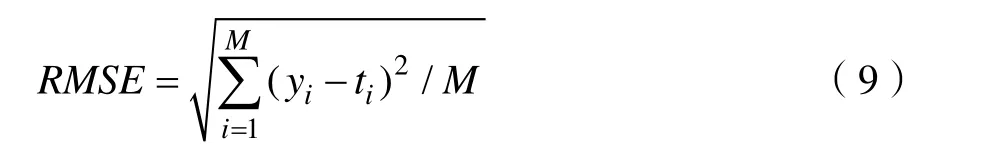
其中，iy为蓄电池剩余寿命的实际测量值，it为蓄电池剩余寿命的预测值，M为实验数据中测试集样本的个数，5号、6号、7号和18号电池的M值分别为68、68、68和32。

BP神经网络、极限学习机ELM和核极限学习机ELM_kernel的预测效果将在后文中列表给出，下图分别给出了 BP神经网络模型的预测输出结果和核极限学习机的预测输出结果，图2为BP神经网络模型的实验结果，图3为核极限学习机的实验结果，其中图（a）、图（b）、（c）和（d）分别为5号、6号、7号和18号电池的实际输出与预测输出。

图2 实验数据和BP神经网络的预测结果Fig.2 The predictions of BP on batteries 5, 6, 7, and 18

表1 各方法的RMSE和时间比较Tab.1 Performance comparisons between different methods

表1的结果表明：（1）在时间指标上，BP神经网络表现出比极限学习机低的性能，而极限学习机的模型性能也劣于增添了核函数的极限学习机，具体表现为，在四种型号电池数据集上，BP神经网络、极限学习机、带核函数的模型平均训练时间分别为3341.5067秒、107.6369秒、0.0116秒；（2）在均方根误差RMSE指标上，尽管在5号电池和7号电池数据集上，极限学习机的结果比反向传输神经网络的结果低了0.2，但是极限学习机在6号和18号电池数据集上的RMSE值优于BP神经网络，而带核函数的极限学习机的表现则比前两者都要好，BP神经网络、极限学习机、带核函数的RMSE值分别为1.47945、1.43175、0.865675。由此得出结论，引入极限学习机可以在取得不错预测性能的基础上有效降低 BP神经网络模型训练时间过长、速度慢的问题，而带有核函数的极限学习机在时间和 RMSE指标值上相较于前两者都有较大提升，对以锂电池为例的蓄电池剩余寿命预测有重要意义。

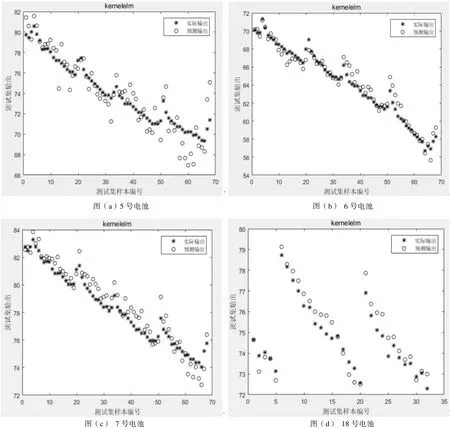
图3 实验数据和核极限学习机的预测结果Fig.3 The predictions of ELM on batteries 5, 6, 7, and 18

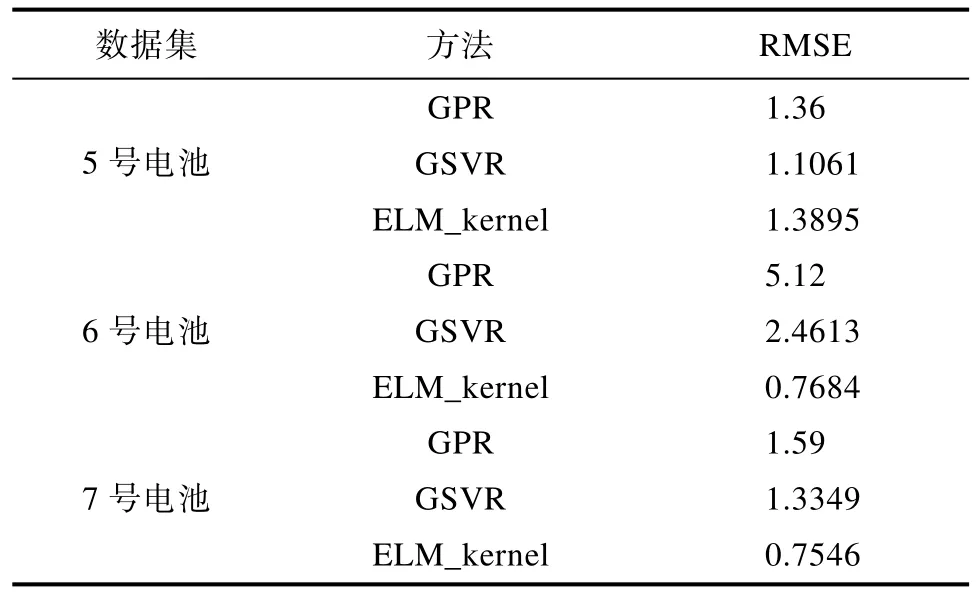
表2 本文方法与其他方法的比较Tab.2 Performance comparisons between the proposed method and other methods.

表1主要为本文运用的几种方法的比较，运用时间指标和RMSE指标对模型性能进行评价，表2展示了核函数极限学习机与其他一些方法的比较。由表2可知，尽管在5号电池数据集上，本文模型的RMSE指标略低于其他方法，具体而言，比高斯过程回归方法GPR高0.0295，比基于高斯过程的支持向量回归GSVR高0.2834；但是，在6号、7号数据集上均比两种方法表现出明显的优势，具体而言，本文方法的RMSE在6号、7号电池数据集上分别比GPR方法低4.3516、0.8354，分别比GSVR方法低1.6929、0.5803。综上所述，ELM_kernel不仅在与本文应用的其他方法比较时表现出优越的时间性能和RMSE指标值，同领域内其他方法比较时也可得出更良好的实验效果，有着其应用价值。

3 结论

通过不同的蓄电池剩余寿命预测模型的建立，可以得知：BP神经网络虽然在使用人工智能方法预测的多个领域表现出它的良好性能，但也有其带来的一些问题，如需人为干预设定一些会对模型性能产生影响的参数、耗时长、学习收敛速度慢和过拟合等问题；极限学习机在一定程度上，弥补了 BP神经网络的不足之处，减少了需设置的参数，改善了耗时问题，提高了训练模型的效率；BP神经网络和极限学习机 ELM 都存在训练模型输出随机的问题，带核极限学习机只要确定核函数的种类和核函数的参数，其输出即为确定值，且带核ELM在时间指标和RMSE指标上都比BP神经网络、极限学习机ELM表现出了更好的性能。

实验验证了极限学习机有助于神经网络模型的预测效果提升、训练时长的减短，可以应用于蓄电池剩余寿命的预测，并预测结果良好。在蓄电池剩余寿命预测中使用核极限学习机，利于我们对系统的监测，以及对可能出现的问题进行预估判断，有其应用价值。

[1] 李文峰, 许爱强, 尹晋, 等. 基于ENN和UKF的电子部件剩余使用寿命预测[J]. 舰船电子工程, 2016, 36(3):106-111. DOI10.3969j.issn.1672-9730.2016.03.028.Li Wenfeng, Xu Aiqiang, Yin Jin, et al. Residual Useful Life Prediction for Electronic Componene Based on ENN and UKF[J]. Ship Electronic Engineering, 2016, 36(3): 106-111.DOI10.3969j.issn.1672-9730.2016.03.028.

[2] 吴婧睿. 基于GSO-ELM的锂离子电池剩余寿命间接预测方法研究[D]. 大连海事大学, 2017.Wu Jingrui. Research on Indirect Prediction Method of Remaining Life Based on GSO-ELM for Lithium-ion Battery[D]. Maritime Affairs University Of Dalian. 2017.

[3] 祁建佳. 基于改进型模糊神经网络的蓄电池SOC检测方法研究与实现[D]. 电子科技大学, 2015.Qi Jianjia. Research and Implementation of Battery SOC Estimation Based on Improved Fuzzy Neural Network[D].University of Electronic Science and Technology of China,2015.

[4] 姜媛媛, 刘柱, 罗慧, 王辉. 锂电池剩余寿命的ELM间接预测方法[J]. 电子测量与仪器学报, 2016, 30(2): 179-185.[2017-09-30]. DOI: 10.13382j.jemi.2016.02.002.Jiang Yuanyuan, Liu Zhu, Luo Hui, Wang Hui. ELM indirect prediction method for the remaining life of lithium-ion battery[J]. Journal of Electronic Measurement and Instrumention,2016, 30(mj02): 179-185. [2017-09-30]. DOI: 10.13382j.jemi. 2016.02.002

[5] 吴海东, 任晓明, 那伟, 等. 改进安时法结合神经网络估算锂离子电池SOC[J]. 电池, 2016, 46(1): 16-19. DOI:10.3969/j.issn.1001-1579.2016.01.005.Wu Haidong, Ren Xiaoming, Na Wei, et al. Estimating SOC of Li-ion battery by improved AH combined with neural network[J]. Battery Bimonthly, 2016, 46(1): 16-19. DOI:10.3969/j. issn.1001-1579.2016.01.005.

[6] 史丽萍, 龚海霞, 李震, 等.基于BP神经网络的电池SOC估算[J]. 电源技术, 2013, 37(9): 1539-1541. DOI:10.3969/j.issn.1002-087X.2013.09.014.Shi Liping, Gong Haixia, Li Zhen, et al. Estimation of battery SOC based on BP neural network[J]. Power Technology,2013, 37(9): 1539-1541. DOI:10.3969/j.issn.1002-087X.2013.09.014.

[7] 戴武昌, 王建国, 徐天锡, 等. 基于神经网络的蓄电池荷电状态估算[J]. 东北电力大学学报, 2016, 36(5): 1-6. DOI:10.3969/j.issn.1005-2992.2016.05.001.Dai Wuchang, Wang Jianguo, Xu Tianxi, et al. Estimation of battery SOC based on neural network[J]. Journal Of Northeast Dianli University, 2016, 36(5): 1-6. DOI:10.3969/j.issn.1005-2992.2016.05.001.

[8] 侯江娜, 孙玉坤, 王鹏飞. 基于RVM算法的蓄电池SOC预测[J]. 电源技术, 2015, (3): 523-526.Hou Jiangna, Sun Yukun, Wang Pengfei. SOC prediction for battery based on relevance vector machine algorithm[J].Power Technology, 2015, (3): 523-526.

[9] 焦慧敏, 余群明. 遗传算法和BP网络在电池电量预测中的研究[J]. 计算机仿真, 2006, (11): 218-220+267.Jiao Huimin, Yu Qunming. Research on Capacity Prediction of Battery based on BP network and Genetic Algorithm[J].Journal of computer simulation, 2006, (11): 218-220+267.

[10] 於东军, 谌贻华, 于海瑛. 融合自组织映射与Wang-Mendel方法的模糊规则提取[J]. 南京理工大学学报(自然科学版), 2011, (6): 759-763.Yu Dongjun, Chen Yihua, Yu Haiying. Fuzzy Rule Extraction by Fusing SOM and Wang-Mendel Method[J]. Journal of Nanjing University of Science and Technology, 2011, (6):759-763.

[11] James Malone, Kenneth McGarry and Stefan Wermter, Data mining using rule extraction from Kohonen self-organising maps, Neural Comput & Applic, 2005, vol.15: 9-17.

[12] Wu J, Wang Y, Zhang X, et al. A novel state of health estimation method of Li-ion battery using group method of data handling[J]. Journal of Power Sources, 2016, 327: 457-464.

[13] Densmore A, Hanif M. Modeling the condition of lithium ion batteries using the extreme learning machine[C]// PowerAfrica,2016 IEEE PES. IEEE, 2016: 184-188.

[14] http://ti.arc.nasa.gov/tech/dash/pcoe/prognostic-data-reposito ry/#Battery.