基于层次分析法的共享单车供求匹配分析
2018-03-23薛子啸李昳晴
张 浩,薛子啸,李昳晴
(1. 华北理工大学机械工程学院,河北 唐山 063200;2. 华北理工大学以升创新基地,河北 唐山 063200)
0 引言
随着共享单车这种新兴交通工具逐渐成为潮流,各种问题也接踵而来[1-3]。其中最主要的便是共享单车的盈利问题,作为一家商业公司,合理的持续收益模式才是长期生存下去的关键,而大部分的共享单车公司的收费标准都十分的低廉,即使单车的成本很高,其收费标准也低至于一小时仅需2元钱。那么,一个既能够满足公众需求,又能够保证公司盈利的定价策略是必要的,而想要建立一个合理的定价策略,首先我们就要分析共享单车资源的供求匹配程度[4-6]。本文通过建立合理的指标,分析不同时空共享单车资源的“供求匹配”程度。在供求匹配中以供给关系和需求关系以及经济影响为准则层进行层次分析,又选取其中六个影响因素和具有代表作用的城市,利用matlab进行判断矩阵的计算并用 SPSS进行因子分析,检验模型的合理性,计算供求之间的匹配程度。

表1 通过n值求RI值的结果Tab.1 The result of the RI value by the n value
1 建立判断矩阵
在供求匹配中以供给关系和需求关系以及经济影响为准则层进行层次分析,又选取其中六个影响因素和具有代表作用的城市,利用matlab进行判断矩阵的计算[7-11],检验模型的合理性,计算供求之间的匹配程度,并建立了供求匹配层次结构模型图如图1所示。
1.1 构造判断矩阵如下:

1.2 计算一致性检验
计算判断矩阵的最大特征根λ及CI:
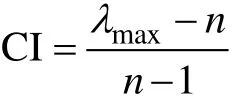
RI值是层次分析法一致性检验过程中用到的查询值:
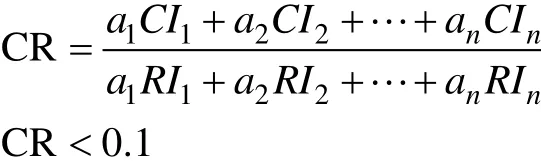
进行检验。若通过,则可按照总排序权向量表示的结果进行决策,否则需要重新考虑模型或重新构造那些一致性比率CR较大的成对判断矩阵。
2 建立模型
由供求匹配的关系可知:你选择的主要标准为共享单车的使用环境,各时段的使用量,使用频率,城市的人口数量,城市共享单车的投放量,共享单车押金的数量,根据统计的数据来构造它们之间的成对比较判断矩阵。设共享单车资源的供求匹配为A,供给影响为B1,需求影响为B2,经济影响为B3。

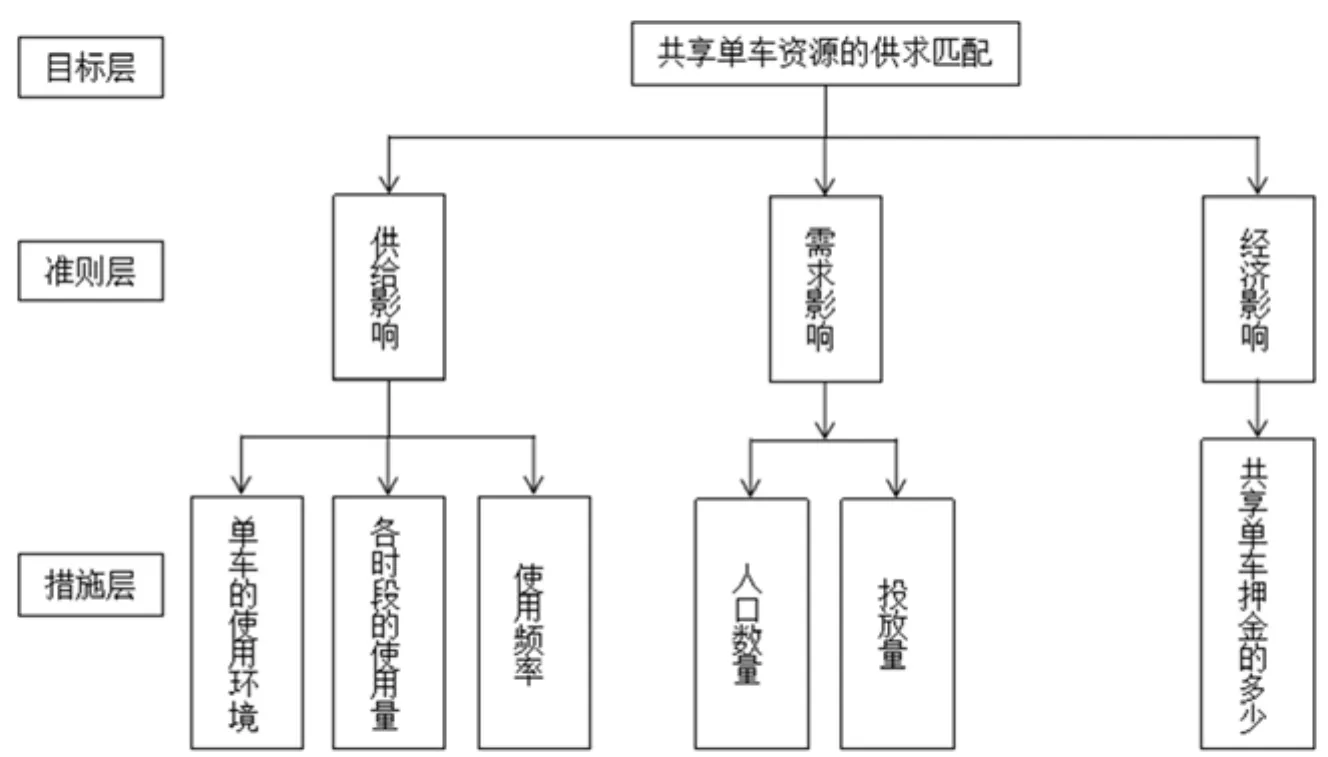
图1 共享单车的供求匹配层次结构模型图Fig.1 The hierarchical structure model of supply and demand matching for shared bicycles
同理可得 B2, B3
由判断矩阵 A 的权重系数[15-17]W =0.46,
1W2= 0 .41,W3= 0 .13,λ= 5 .99,CRA= 0 .0535。
由判断矩阵 B 的权重系数 W1= 0 .19W2=0.43,W3= 0 .28,W4= 0 .58,W5= 0 .42,W6= 1 。
λ =5.34,CRB1=0.075
同理可得 C RB2,CRB3同时<0.1,可得判断矩阵的一致性是可以接受的。
由准则层权重 W1> W2> W3可得供给影响与需求影响对供求匹配的影响所占比重比较大,说明供求匹配的程度大,而且供给量大于需求量,经济影响的供求匹配程度小。
在判断矩阵B中 W4> W2> W5,供求匹配影响与各时段的使用,城市人口数量和城市共享单车投放量具有密切联系[18-20]。
分析不同城市与不同时间段共享单车的供求匹配关系并通过SPSS计算[12-14]得到表2,表3。
3 结论
本文在供求匹配中以供给关系和需求关系以及经济影响为准则层进行层次分析,又选取其中六个影响因素和具有代表作用的城市,利用matlab进行判断矩阵的计算并用 SPSS进行因子分析,便能够得到这六个城市的共享单车供求匹配关系,而通过这种方法,结合实际的数据,也同样能够计算出其他城市的共享单车的供求匹配关系,进而能够以此为基础,来建立一个合理的既能满足公众需求,又能够保证公司盈利的定价策略。
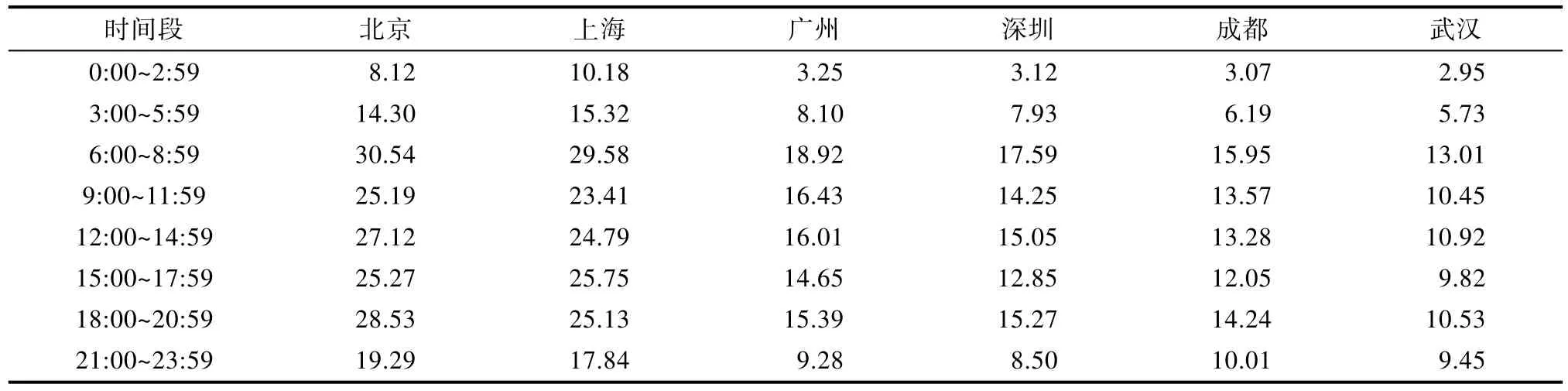
表2 共享单车在各地区不同时间段的使用量(万)Tab.2 The use of a single vehicle for different periods of time in each area (ten thousand)

表3 各地区供求匹配程度等级一览表Tab.3 The list of matching levels of supply and demand in each region
[1] 李琨浩. 基于共享经济视角下城市共享单车发展对策研究[J]. 城市, 2017(03): 66-69.
[2] 程陈. 大数据挖掘分析[J]. 软件, 2014, 35(4): 130-131.
[3] 李敏莲. 共享单车市场调研与分析[J]. 财经界(学术版),2017(05): 121-123.
[4] 周勇君, 蒋迪, 祝源, 杜丽萍. “互联网+”时代出租车供求匹配程度的评价[J]. 河北联合大学学报(自然科学版),2016, 38(02): 117-120.
[5] 费威, 马跃, 李泊宁, 李昆. 我国城市出租车资源供求匹配程度研究[J]. 河北科技大学学报(社会科学版), 2016,16(01): 1-7.
[6] 朱家明, 刘玲, 孟康, 桂安琪. 基于AHP-熵值的不同时空出租车资源供求匹配研究——以上海市为例[J].太原师范学院学报(自然科学版), 2016, 15(01): 52-58.
[7] 徐泽水, 刘海峰. 六类不确定型判断矩阵的相容性研究[J].模糊系统与数学, 2003(02): 53-58.
[8] 吴泽宁, 张文鸽, 管新建. AHP中判断矩阵一致性检验和修正的统计方法[J]. 系统工程, 2002(03): 67-71.
[9] 储敏. 层次分析法中判断矩阵的构造问题[D]. 南京理工大学, 2005.
[10] 余沐坡, 王积社. 两个矩阵同时若当标准化的MATLAB程序[J]. 软件, 2013, 34(9): 68-69.
[11] 刘波, 郭平, 沈岳, 等. 农业文本特征重组向量矩阵算法优化与仿真[J]. 软件, 2015, 36(4): 6-13.
[12] 王斌会, 李雄英. 稳健因子分析方法的构建及比较研究[J].统计研究, 2015, 32(05): 84-90.
[13] 俞立平, 刘爱军. 主成分与因子分析在期刊评价中的改进研究[J]. 情报杂志, 2014, 33(12): 94-98.
[14] 范会勇. 因子分析的元分析技术及其应用[J]. 心理科学进展, 2011, 19(02): 274-283.
[15] 邓雪, 李家铭, 曾浩健, 陈俊羊, 赵俊峰. 层次分析法权重计算方法分析及其应用研究[J]. 数学的实践与认识,2012, 42(07): 93-100.
[16] 郭金玉, 张忠彬, 孙庆云. 层次分析法的研究与应用[J].中国安全科学学报, 2008(05): 148-153.
[17] 刘江. 基于层次分析法的企业运输方式的选择[D]. 对外经济贸易大学, 2006.
[18] 龚江, 石培春, 李春燕. 使用SPSS软件进行多因素方差分析[J]. 农业网络信息, 2012(04): 31-33.
[19] 邹祎. SPSS软件单因素方差分析的应用[J]. 价值工程,2016, 35(34): 219-222.
[20] 王宏志, 朴东升. 多关系中基于层次的实体识别算法[J].新型工业化, 2012, 2(12): 56-68.
