一种基于抛物线预测去卷叠的LFM参数估计方法

刘 康，陈 政

（昆明理工大学信息工程与自动化学院，云南 昆明 650504）

0 引言

线性调频信号因其具有大时宽、带宽积、距离分辨率高、低峰值功率等优良特性而广泛应用于通信、雷达、地震勘探等领域，其频率特征的提取是估计参数最重要的问题之一，也是相关领域重要的研究内容。

作为最常用的非平稳信号之一，在一些情况下，对于LFM信号频率特性的快速、精确估计显得尤为重要，传统具有代表性的估计方法有：各种基于最大似然估计的算法，该类算法估计精度高，但运算量大，不利于工程上的快速实现[1-3]；一些以短时傅里叶变换（STFT）、分数阶傅里叶变换（FrFT）为代表的时频分析方法[4-8]充分利用了 LFM 信号的时频聚集特性，也可用于该信号的参数估计，但需复杂的搜索和计算，同样有待研究改进。总的来说，提出一种不需要参数搜索的快速、精确的线性调频信号参数估计方法具有重要的现实意义，本文基于文献[9]中提及的使用希尔伯特变换提取出的瞬时相位会产生卷叠的问题[9]，提出了一种新的去卷叠方法，新方法具有计算简单、易于实现、能真实还原相位的特点。

1 LFM信号瞬时相位及频率分析

不失一般性，假设接收到的线性调频实信号表达式为：

其中：1f为调频率，0f为起始频率，0φ为初始相位，这里1f和0f为待估参数，由（1）式可知，LFM信号的瞬时相位可表达为：

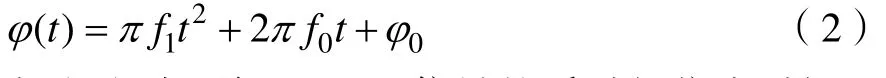
由（2）式可知，LFM信号的瞬时相位为时间t的二次函数，因此只要提取信号的瞬时相位，再对提取的瞬时相位利用二次多项式 y = a x2+ b x + c 进行拟合，根据拟合获得的二次式系数与参数 f1和 f0的对应关系，即可得到参数估计值。

对式（1）表达的信号进行希尔伯特变换，并将信号表示为解析信号的形式：

其实部、虚部分别表达为：

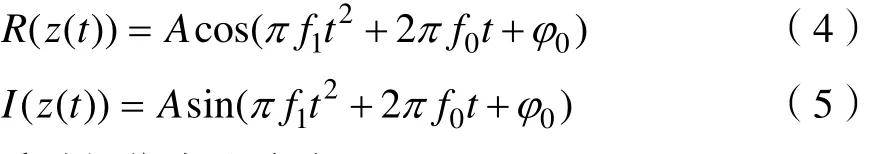
瞬时相位表达式为：

利用希尔伯特变换构建解析信号，然后计算（6）式的反正切函数值即可得到瞬时相位。

2 抛物线预测去卷叠算法原理

通过反正切函数计算出的相位值域在/π-2~/2π之间，按模π计算相位序列会使相位发生卷叠，因此需对得到的相位进行去卷叠，此时引入抛物线预测矩阵[10]：

考虑一个形式为二次多项式的信号：

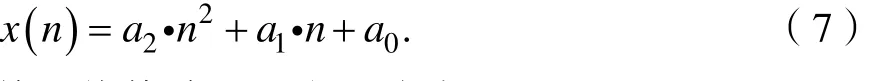
其无偏估计可以由下式表示：

其中 hl（ i）是受高斯白噪声影响的系数，在没有噪声影响的情况下xˆ( n ) = x( n)，若各系数中的噪声统计独立，那么噪声的功率为：

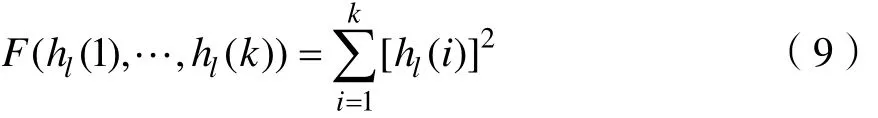
各项约束条件为：

为使噪声的功率最小，使用拉格朗日乘子法，可得拉格朗日方程：

其中jλ可由下面的矩阵方程解得：

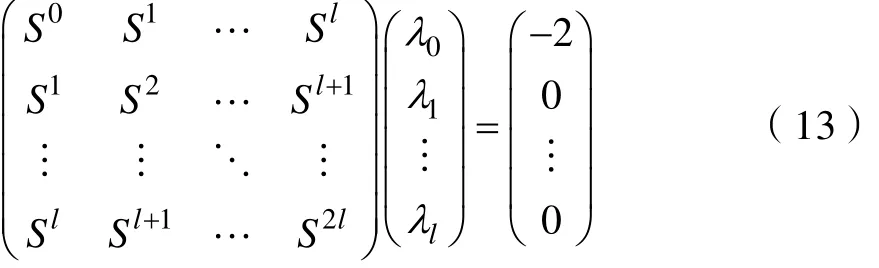
K=3 时，系数 h（1）=3，h（2）=-3，h（3）=1，即： x ( n ) = 3 x( n - 3 )- 3 x( n - 2 ) + x ( n - 1 )写成矩阵形式： F = [ 3 - 3 1]. 得到预测系数矩阵后，即可根据前三个相位值预测下一个相位，然后将预测相位和反正切值进行比较、修正，即可还原真实相位，达到去卷叠的目的。

使用多项式最优系数阵可以对瞬时相位进行去卷叠处理，处理后的瞬时相位仍会存在部分异常点，本文使用最小二乘对瞬时相位序列进行拟合，减少异常点对参数估计精度的影响，同时根据得到的瞬时相位使用高阶差分计算瞬时频率[11]，可以降低噪声的影响。

3 算法仿真

本节通过仿真实验来验证本文算法的参数估计性能。选用的LFM信号为 u ( t) = c os(10 t + 2 0 t2)，采样频率f s =1 kHz，采样点数N =1 024点，噪声为加性高斯白噪声，信噪比 15 dB，文献[8]中利用希尔伯特变换提取的未进行去卷叠处理的瞬时相位如图（1）所示。

使用本文抛物线预测去卷叠方法处理后得到的真实相位如图2所示。

瞬时相位、瞬时频率拟合得到参数估计结果如表（1）所示，初始频率真值为10 rad/s，参数估计结果为10.1288 rad/s，调频斜率真值为40 rad/s^2，参数估计结果为 39.9024 rad/s^2。证明本文方法能有效用于LFM信号参数估计中的相位卷叠问题。

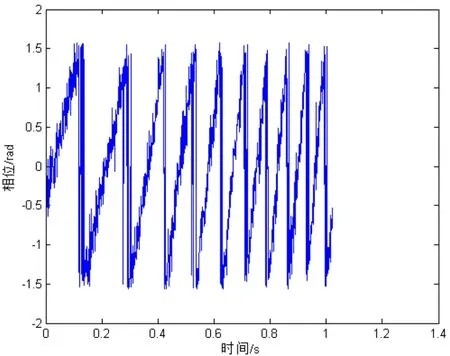
图1 未进行去卷叠处理的瞬时相位Fig.1 The phase without Unwrapping

图2 抛物线预测去卷叠后的瞬时相位Fig.2 The phase by using the Parabola Prediction

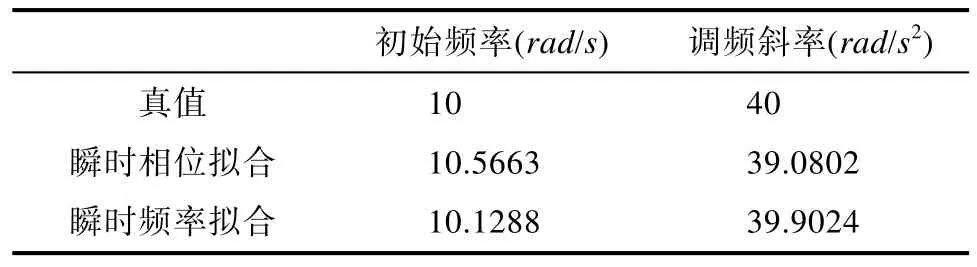
表1 参数估计结果Tab.1 results of parameters estimation

4 结束语

传统的线性调频信号参数估计算法往往需要大量的搜索和计算，这给参数估计带来了困难。本文基于文献[9]中在提取瞬时相位的过程会发生相位卷叠的问题提出了一种新的去卷叠方法，并简述了算法原理，以及仿真分析。新方法具有计算简单、易于实现、能真实还原相位的特点，仿真实验说明了本文算法的有效性。

[1] Peter O’Shea. A Fast Algorithm for Estimating the Parameters of a Quadratic FM Signal[J]. IEEE Transactions On Signal Processing, 2004, 52(2): 385-393.

[2] Abatzoglou T. Fast Maximum Likelihood Joint Estimation of Frequency and Frequency Rate[J]. IEEE Trans on AES, 1986,22(6): 708-715.

[3] Liang R M, Arun K S. Parameter Estimation for Superimposed Chirp Signals[C]// IEEE International Conference on ASSP, San Francisco, CA: [s.n.], 1992: 273-276.

[4] 齐林, 陶然, 周思永, 等. 基于分数阶Fourier变换的多分量LFM信号的检测和参数估计[J]. 中国科学(E), 2003,33(8): 749-759.QI L, TAO R, ZHOU S Y, et al. Detection and Parameter Estimation for The Multi-Component LFM Signal Based on Fractional Fourier Transform[J]. SCIENCE CHINA (E),2003, 33(8): 749-759.

[5] 张希会. 线性调频波检测与估计的简化探讨[D]. 电子科技大学, 2007. 1-3.ZHANG X H. A simplified approach to the detection and estimation of LFM waves[D]. University of Electronic Science and Technology of China, 2007. 1-3.

[6] 袁振涛, 胡卫东, 郁文贤. 用FrFT插值实现LFM信号的参数估计[J]. 信号处理, 2009, 25(11): 1726-1731.YUAN ZH T, HU W D, YU W X. Parameter Estimation of LFM Signals Using FrFT Interpolation[J]. SIGNAL PROCESSING, 2009, 25(11): 1726-1731.

[7] Roshen J, Tessamma Thomas. Applications of Fractional Fourier Transform in Sonar Signal Processing[J]. IETE Journal of Research, 2009, 55(1): 16-26.

[8] 陈蓉, 汪一鸣. 一种新的基于分数阶Fourier变换的线性调频信号的参数估计方法[J]. 新型工业化, 2011, 1(2): 84-92.CHEN R, WANG Y M. A Novel Parameter Estimation Method of LFM Signals Based on Fractional Fourier Transform[J]. New Industrialization Straregy, 2011, 1(2): 84-92.

[9] 张西托, 饶伟, 黄信荣, 陈珊珊. LFM信号参数估计算法研究[J]. 雷达科学与技术, 2009, 7(03): 219-221.ZHANG X T, RAO W, HUANG X R, CHEN SH SH. Algorithm Research for Parameter Estimation of LFM Signals[J].Radar Science and Technology, 2009, 7(03): 219-221.

[10] P. Heinonen, Y. Neuvo. FIR-median hybrid filters with predictive FIR substructures. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1988, 36(6): 892-899.

[11] 张春杰, 郜丽鹏, 司锡才. 瞬时相位法线性调频信号瞬时频率提取技术研究[J]. 弹箭与制导学报, 2006, 26(3):290-292.ZHANG CH J, G L P, S X C. Research on Distilling Instant Frequency of LFM Signals Based on Phase[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2006, 26(3):290-292.