基于卡尔曼滤波的抗电离层闪烁跟踪算法研究

夏 俊，周必磊，宋 涛，刘 阳，岳富占

(1. 上海卫星工程研究所，上海 201109； 2. 北京卫星信息工程研究所，北京 100086)

0 引言

星载GPS接收机作为低轨卫星、载人飞船及空间站等低轨航天器的重要测控手段，主要为航天器提供实时定位、授时、定轨服务，其性能对实现航天器任务的高分辨率、高精度、高稳定性和高可靠性等指标要求具有至关重要的影响。低轨航天器多工作在高度低于1 000 km的轨道[1]，电离层闪烁现象较为严重，且电离层闪烁与工作频率有关，在3 GHz频率以下，电离层闪烁最为严重。GPS系统恰好工作在L频段，故电离层闪烁严重影响星载GPS接收机的性能，不仅会降低接收机的环路跟踪性能，当闪烁特别严重时，还会造成接收机的环路失锁，以致无法定位[2]。故电离层闪烁现象已成为星载GPS接收机亟待解决的难点问题。

文献[3-4]中提出了闪烁下环路参数的合理设计；文献[5]中提出了一种采用电文剥离技术提高环路抗电离层闪烁性能的方法；文献[6]中利用由MITRE建立的电离层闪烁仿真模型，分析对比了采用不同鉴别器的环路抗闪烁性能；文献[7-9]中分析了锁频环(FLL)辅助锁相环(PLL)跟踪环路的抗闪烁跟踪性能。

以上研究结果表明:仅通过环路参数、鉴相器的选择，传统PLL环路当电离层闪烁时并不能很好地适应，且以上跟踪环路具有环路带宽固定的问题，环路带宽的选取始终需要在跟踪鲁棒性与跟踪精度之间做平衡。理论上，采用自适应带宽环路是抗电离层闪烁的一种有效途径。本文提出一种基于卡尔曼滤波的抗电离层闪烁跟踪算法，介绍电离层闪烁理论模型及闪烁数据的生成过程，给出卡尔曼滤波跟踪环路结构，建立卡尔曼滤波跟踪模型并加以仿真。

1 电离层闪烁理论模型

1.1 理论模型

AJ-Stanford模型是一种常用的电离层闪烁信号统计模型，它是基于大量实验数据的统计特性而被提出，用于模拟产生电离层闪烁时信号幅度和相位变化量的时间序列。

AJ-Stanford模型将电离层闪烁信号表示为

E=Aexp(jφ)=A0δAexp[j(φ0+δφ)]

(1)

式中：A0为信号的正常幅度；δA为电离层闪烁影响下的信号幅度变化；φ0为正常信号的载波相位；δφ为闪烁影响时的相位变化。当无电离层闪烁时，δA为1，δφ为0；当电离层闪烁时，δφ与δA会发生随机起伏变化。电离层闪烁时信号功率(I=A2=I0δI)的变化量δI服从Nakagami-m分布，概率密度函数[10]可表示为

(2)

式中：δI为信号功率变化量；Ω=E(δI)为信号强度均值;1/m为Nakagami-m分布的方差;Γ(m)为Gamma函数。

由电离层闪烁造成的信号幅度衰落强度用S4因子表示(即幅度闪烁因子)，其定义为信号功率变化量的归一化标准差，即

(3)

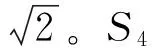
m=1/(S4)2

(4)

对于闪烁信号的强度谱具有幂律特征，可以利用幂指数即对数域的斜率来反映闪烁特征。

闪烁信号相位起伏通常服从零均值高斯分布，即

(5)

式中：σ为相位变化的标准差(即相位闪烁因子)。

相位变化在短时间间隔内是强相关的。同时，闪烁信号相位谱也具有幂律特征，观测到的功率谱密度近似遵循Tf-p的形式，其中谱斜率p的范围为2.0～3.0，其中T为强度因子(单位为rad2/Hz)。

1.2 闪烁数据生成

总体来说，幅度与相位的变化具有负相关性，即较大的幅度变化对应于较小的相位变化，反之亦然。实验数据表明:该相关系数约为-0.6。此相关性可通过一个双变量变化来表示，即

(6)

式中：δI和η分别为两个独立的高斯序列，其中δI的方差为σI、均值为Ω，η是均值为0、方差为1的高斯随机数；ρφI为信号功率变化量与相位变化量的相关系数；相位的变化量δφ可由δI、η、ρφI联合求解得到。为不将偏差引入δφ，将δI减去均值Ω,等频谱成型后再将此均值加回即可。

为使产生的数据具有期望时间相关性，即接近于实验观测数据的谱形状，模型使用成型滤波器对时间序列进行滤波。成型滤波器中使用一组级联的Butterworth滤波器来实现，即

(7)

式中：H(jf)为传递函数;f为频率;mk与ml为滤波器阶数;an、bn、c与d为滤波器系数。从式(7)可以看出，此滤波器由一系列带通滤波器以及一个低通滤波器和一个高通滤波器级联而成，共同形成了闪烁强度谱和相位谱的形状。k是一个尺度因子，保证S4和σ在通过此滤波器后，大小不被改变。即k必须满足

(8)

对于幅度闪烁，整形滤波器的参数可表示为

(9)

AJ-Stanford模型闪烁信号生成过程如图1所示。

图1 基于AJ-Stanford模型的电离层闪烁数据生成流程Fig.1 Process of ionospheric scintillation data generation based on AJ-Stanford model

首先由两个高斯序列发生器基于S4和σ驱动产生两个高斯序列，然后这两个高斯序列再通过矩阵变换根据设定的相关系数ρφI作相关运算，相关后的结果经过整形滤波，使谱形状满足幂律特征。其中的信号幅度经整形滤波后通过一个Gamma分布适配器，再经平方根操作将高斯分布的信号幅度序列转化为Nakagami-m分布。幅度变化序列δA乘以正常信号幅度值A0产生最终的信号幅度。同时，将相位起伏序列δφ加在正常的相位上以形成最终的信号相位，最终形成所需要的电离层闪烁信号。

2 卡尔曼滤波跟踪环路

运用卡尔曼滤波技术跟踪GPS卫星信号的前提是假设GPS卫星信号参数变化为由一个白噪声驱动的随机信号模型。卡尔曼滤波方程分为系统状态方程和系统观测方程，系统状态方程主要完成状态参量和状态估计误差的传递，系统观测方程主要负责从系统观测量获取用于修正状态量的信息，实现信号参数跟踪，其中状态模型采用状态空间法对系统状态量建模，观测模型主要提供系统修正所需的信息[11]。

图2是基于卡尔曼滤波的载波跟踪环路原理图，与传统跟踪环路不同的是，利用卡尔曼滤波器完成载波相位的跟踪，本地复现载波NCO(数控振荡器)频率更新来自于卡尔曼滤波的处理结果。

图2 基于卡尔曼滤波的载波跟踪环路原理图Fig.2 Diagram of carrier tracking loop based on Kalman filter

2.1 系统状态方程建立

离散卡尔曼滤波的状态方程为

Xk=ΦXk-1+Wk-1

(10)

(11)

式中：Qk为系统噪声Wk的2×2维对称非负定方差矩阵；δkj为Kronecker-δ函数。

2.2 系统观测方程建立

离散卡尔曼滤波的观测方程为

Zk=HXk+Vk

(12)

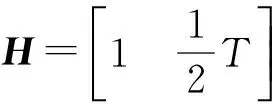
(13)

式中：Rk为观测噪声Vk的1×1维对称正定方差矩阵。

载波跟踪环路鉴别器选取为二象限反正切鉴别器，则观测量大小Zk可表示为

(14)

式中：Qp,k与Ip,k分别为k时刻Q支路与I支路累加值。

2.3 卡尔曼滤波过程

基于状态转移方程的状态向量的一步预测方程为

(15)

基于一步预测方程与观测方程的状态滤波方程为

(16)

式中：Kk为滤波增益矩阵，即

Kk=Pk/(k-1)HT(HPk/(k-1)HT+Rk)-1

(17)

为计算滤波增益矩阵Kk，需要计算一步预测误差的方差阵，表示为

Pk/(k-1)=ΦPk-1ΦT+Qk-1

(18)

相应的估计误差的方差阵为

Pk=(I-KkH)Pk/(k-1)

(19)

上述的式(15)～(19)即为随机线性离散系统中卡尔曼滤波算法的5个基本公式。

3 仿真分析

基于Matlab语言数值仿真验证卡尔曼滤波跟踪环路抗电离层闪烁的性能。图3给出了幅度闪烁因子(S4=0.5或0.9,σ=0.1)时基于AJ-Stanford模型生成的闪烁信号。

图3 采用AJ-Stanford模型当幅度闪烁不同 时生成的电离层闪烁数据Fig.3 Ionospheric scintillation data with different amplitude scintillations based on AJ-Stanford model

以中等幅度闪烁信号(S4=0.5,σ=0.1)为例，统计分析跟踪结果。卡尔曼滤波环路中，Q矩阵分别设置为[0.01 0; 0 0.1]、[0.01 0; 0 0.1]、[0.01 0; 0 0.01]，对应的R分别设置为10、5与5。

针对中等幅度闪烁，分别统计以上3组不同参数卡尔曼环路鉴相值标准差最大值及载波相位误差，统计结果如表1所示。

表1 S4=0.5,σ=0.1时不同参数卡尔曼环路跟踪结果

由表1可知，当中等幅度闪烁，R取5时的环路载波相位误差大于R取10时的环路载波相位误差；R取5时，Q22取0.1时的环路载波相位误差比Q22取0.01时的载波相位误差稍大。故当发生电离层幅度闪烁时，为降低环路热噪声，提高载波相位跟踪精度，需要减小Q值，增大R值。

图4给出幅度闪烁不同时不同参数卡尔曼环路与PLL环路鉴相器输出值的标准差，图5给出了幅度闪烁不同时卡尔曼环路与PLL环路载波相位误差。由图4可知，幅度闪烁不同时，3组不同参数卡尔曼环路鉴相值标准差基本相当，卡尔曼环路在幅度闪烁时的鉴相值标准差比PLL环路小，当环路稳定跟踪时卡尔曼环路具有比PLL环路更小的等效带宽，跟踪鲁棒性要优于PLL环路。由图5可知，卡尔曼环路在幅度闪烁时的载波相位误差同样比PLL环路小。故当幅度闪烁时，卡尔曼环路的跟踪精度要明显优于PLL环路。

图4 幅度闪烁不同时卡尔曼环路与PLL环路鉴相值标准差Fig.4 Standard deviation of discriminator output of Kalman and PLL loops with different amplitude scintillations

图5 幅度闪烁不同时卡尔曼环路与PLL环路载波相位误差Fig.5 Carrier phase error of Kalman and PLL loops with different amplitude scintillations

4 结束语

针对电离层闪烁可引起星载GPS接收机传统PLL跟踪环路测量误差增大从而降低接收机定位及测速精度的问题，提出了一种卡尔曼滤波环路抗电离层闪烁算法。仿真结果表明：幅度闪烁时，为提高载波相位跟踪精度，需要减小Q值，增大R值；且与传统的PLL环路相比，卡尔曼滤波算法跟踪鲁棒性与跟踪精度明显优于PLL环路。但由于卡尔曼滤波算法是一系列的矩阵运算，计算量较大，针对未来的工程应用，需要重点解决卡尔曼环路在星上资源受限时的算法优化实现问题。

[1] 徐福祥, 林华宝, 侯深渊. 卫星工程概论[M]. 北京: 中国宇航出版社, 2003.

[2] 刘钝, 甄卫民, 冯健, 等. 电离层闪烁对卫星导航系统性能影响的仿真分析[J]. 全球定位系统, 2011, 36(2): 7-12.

[3] HUMPHREYS T. GNSS and ionospheric scintillation: How to survive the next solar maximum[J]. Inside GNSS, 2009, 4(4): 22-30.

[4] HUMPHREYS T E, PSIAKI M L, HINKS J C, et al. Simulating ionosphere-induced scintillation for testing GPS receiver phase tracking loops[J]. IEEE Journal of Selected Topics in Signal Processing, 2009, 3(4): 707-715.

[5] HUMPHREYS T E, PSIAKI M K, KINTNER P M. Modeling the effects of ionospheric scintillation on GPS carrier phase tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(4): 1624-1637.

[6] YU W, LACHAPELLE G, SKONE S. PLL performance for signals in the presence of thermal noise, phase noise, and ionospheric scintillation[C]∥Proceedings of the 19th International Technical Meeting of the Satellite Division of The Institute of Navigation. Fort Worth, TX: The Institute of Navigation, 2006: 1341-1357.

[7] ZHANG L, MORTON Y T. Tracking GPS signals under ionosphere scintillation conditions[C]∥Proceedings of ION GNSS 2009. Savannah, GA: The Institute of Navigation, 2009: 227-234.

[8] ZHANG L, MORTON Y, van Graas F, et al. Characterization of GNSS signal parameters under ionosphere scintillation conditions using software-based tracking algorithms[C]∥Position Location and Navigation Symposium. Indian Wells, CA: Aerospace and Electronic Systems Society, 2010: 264-275.

[9] MAO X L, MORTON Y T, ZHANG L, et al. GPS carrier signal parameters estimation under ionosphere scintillation[C]∥23th International Technical Meeting of the Satellite Division of The Institute of Navigation. Portland, OR: The Institute of Navigation, 2010: 3277-3283.

[10] SKONE S, LACHAPELLE G, YAO D, et al. Investigating the impact of ionospheric scintillation using a GPS software receiver[C]∥ION GNSS 18th International Technical Meeting of the Satellite Division. Long Beach, CA: The Institute of Navigation, 2005: 1126-1137.

[11] 夏俊, 岳富占, 董启甲, 等. 基于滑动相关的抗电离层闪烁跟踪算法研究[J]. 自动化技术与应用, 2016, 35(5): 67-71.