基于Matlab的电子式互感器传变特性仿真研究
2018-03-22金世鑫金晓非李籽良耿莉娜
金世鑫 , 李 华 , 金晓非 , 李籽良, 耿莉娜
(1.国网辽宁省电力有限公司电力科学研究院,辽宁 沈阳 110006;2.国网辽宁省电力有限公司经济技术研究院,辽宁 沈阳 110015;3.国网大连供电公司,辽宁 大连 116011)
在实际运行中,电子式互感器体现出相对于传统互感器的巨大技术优势,并随着技术的发展、工艺和设计的改进以及运维经验的丰富,电子式互感器会得到越来越广泛的应用。
1 罗氏线圈电流互感器工作原理
基于罗氏线圈电子式电流互感器结构如图1所示,其基本原理是利用漆包线均匀缠绕在空心骨架上,利用互感原理来测量一次电流的大小,输出量为电流的微分信号。基于罗氏线圈电子式电流互感器主要分为5个工作单元:传感单元(罗氏线圈)、电源单元、高压侧数据采集单元、光纤传输单元和低压侧合并单元,工作原理如图2所示[1]。经过罗氏线圈传感头的电流信号会转变成模拟电压信号,这一电压信号由高压侧数据采集单元的信号处理电路解析为数字脉冲信号,光电转换后变换为光信号,光信号通过光纤传输单元传送到低压合并单元后转换为电信号,再经放大处理后送入保护系统。其中高压侧数据采集系统中的积分电路是信号处理电路中的极重要环节之一,确保整个测量系统精度的前提便是要保证积分信号的准确。
2 基于Matlab的罗氏线圈电子式互感器传变特性仿真
2.1 积分电路分析
典型的积分电路包含一阶无源积分器、理想有源积分器和负反馈积分器。无源积分电路不包含运放,其在低频段的工作特性比较差,而在高频段特性较好,当频率较低时,并联电容的容抗值很大,无源积分电路实际就是一个电阻电路[2]。理想积分器结构简单,但是存在温漂、电流偏置、电压失调等问题,这些不利因素不断积累,会造成信号叠加产生积分漂移,最终导致积分器饱和,失去积分作用。因此,适合作为理论研究,但不具有实用价值。负反馈积分器是在理想积分器的电容上增加一个并联电阻,其在高频段特性较好,而在低频段特性差。但这种积分器在低频段时对被测信号有放大效果,增益可能远超工频信号,工作稳定性差[3]。综合考虑上述常见各种积分器的优缺点,为了满足互感器测量宽带的要求,典型的无源积分电路与有源积分电路级联组成的级联积分器得到推广,电路结构如图3所示,图4为绘制的简单幅频特性,图5为级联积分器与理想积分器的幅频特性仿真。由图4可以看出级联积分器的参数选择合适的情况下,其幅频特性连续,性能良好。图5验证了图4得到的结果,进一步证明参数能够良好配合的级联积分器有较宽的工作频带,在低频段的频率特性也不会受到低频信号的干扰,工作性能良好。

图1 罗氏线圈结构

图2 罗氏线圈工作原理
2.2 低通滤波电路分析
罗氏线圈的输出电压难免会受到高频信号的干扰,为解决这一问题,需要在积分电路后增加滤波电路单元。最常用的低通有源滤波电路有3种,即巴特沃思、切比雪夫和贝塞尔滤波电路[4]。巴特沃思低通滤波器的传递函数标准形式为
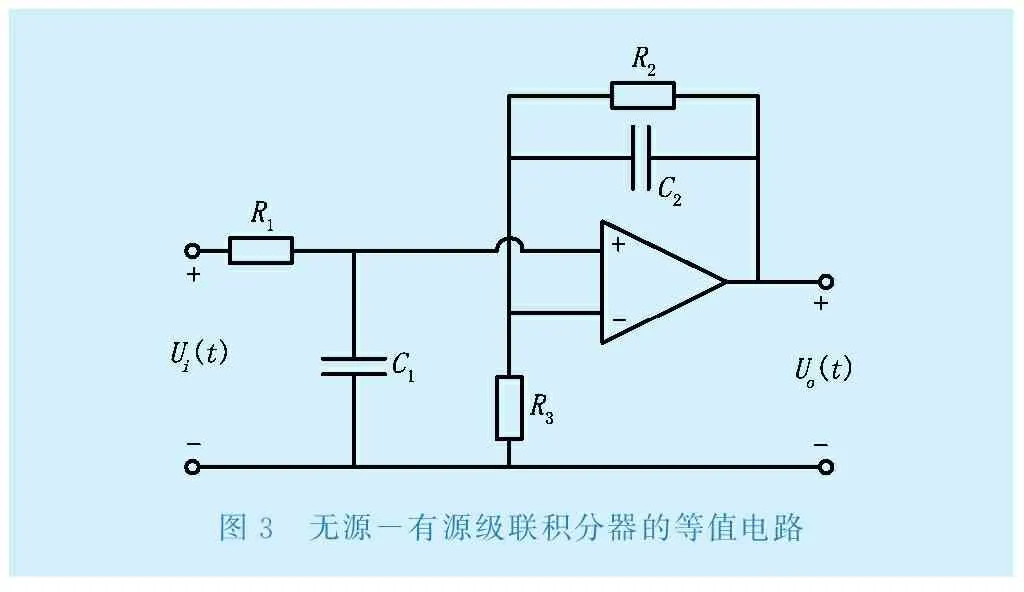
图3 无源-有源级联积分器的等值电路
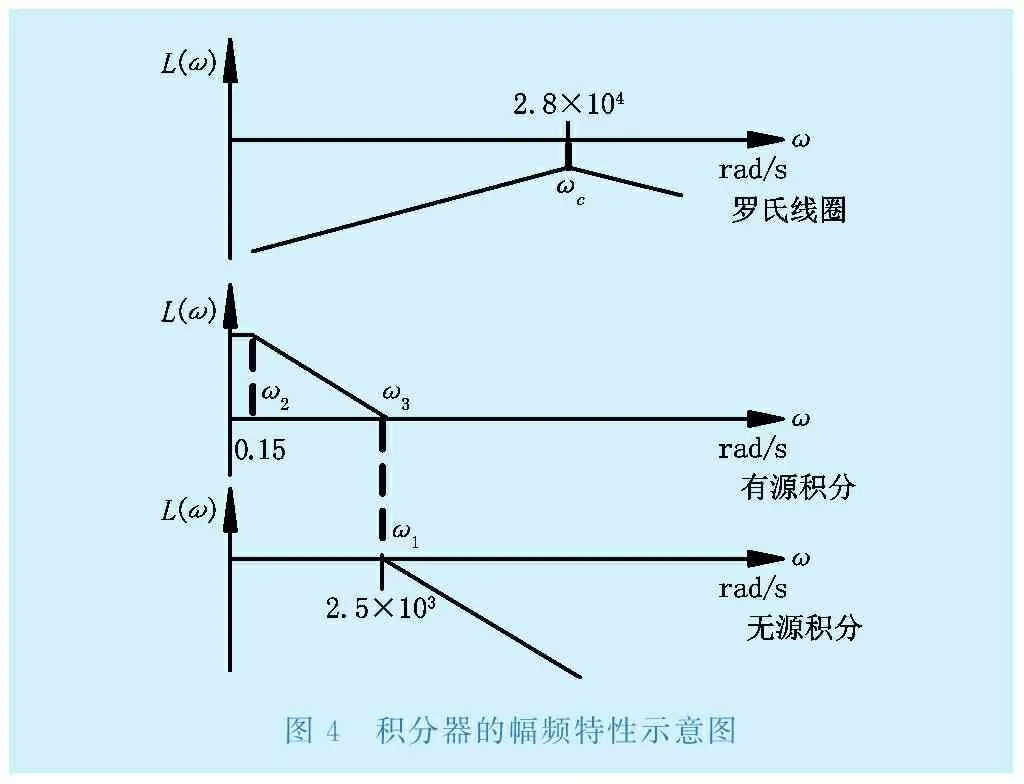
图4 积分器的幅频特性示意图
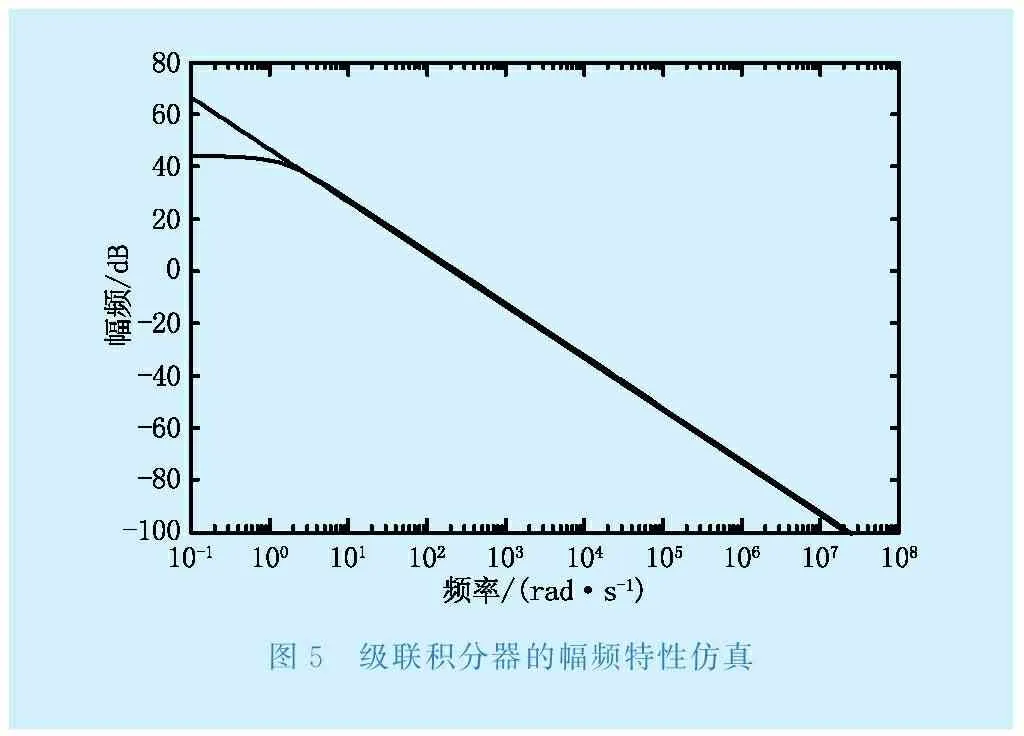
图5 级联积分器的幅频特性仿真
(1)
式中:B、C为巴特沃思归一化系数,k为增益常数。有源巴特沃思低通滤波器的等值电路如图6所示。查询巴特沃思低通滤波器的公式化设计数据表格,设计的参数为C1=10 pF;C2=2.2 nF;R1=110 kΩ;R2=220 kΩ;R3=568.2 kΩ。
利用Matlab中的simulink建立低通滤波器数学模型,低通滤波器的频率特性如图7所示,可以看出低通滤波器的幅频和相频特性在低频段很稳定,在高频段随着频率的不断上升逐渐衰减为零。

图6 有源低通滤波器的等值电路
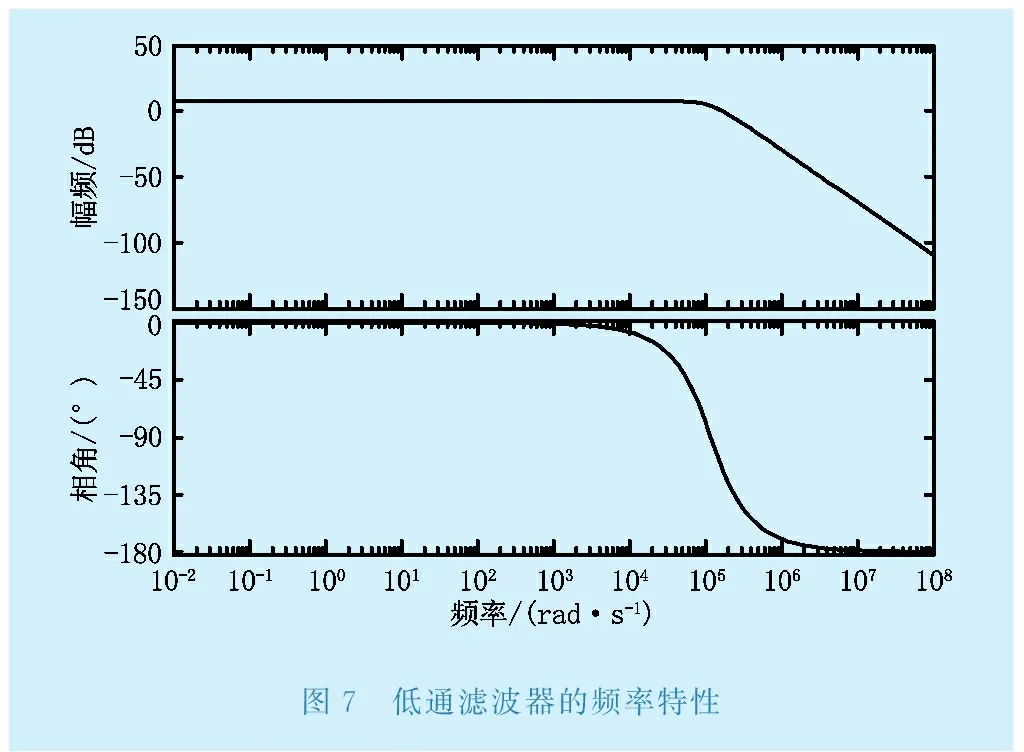
图7 低通滤波器的频率特性
2.3 移相电路分析
移相器的作用是在一定频段内改变传递函数的相频特性,而对其幅频特性没有影响,移相器的等值电路如图8所示,通过图8可以求得其传递函数,通过调节电阻的数值能够改变移相的角度,为了实现较好的移相效果,需要满足R2R3=4R1R4且C1=C2,查询移相器的标准设计参数,确定电容C1、C2的标称值为0.5 nF。求得各电阻值为R1=7.66 kΩ;R2=10.3 kΩ;R3=21.24 kΩ;R4=7.08 kΩ。利用Matlab中的simulink建立移相器的数学模型,通过仿真得到移相器的频率特性如图9所示,从图9中可以看出在103~107 rad/s频带范围内,移相器具有相位补偿的作用,对幅频特性则没有影响。
2.4 罗氏线圈电流互感器频率特性仿真分析
根据电子式电流互感器各环节的工作原理,建立基于罗氏线圈电流互感器的整体仿真模型,如图10所示。模型中包括罗氏线圈等效电路在内的各个部分是串联关系[5]。
利用Matlab仿真,得到基于罗氏线圈电流互感器模型的频率特性如图11所示。由图9可以看出,罗氏线圈电流互感器的工作频带大概范围为0.237 ~27 600 rad/s,因此在这段频率范围内的幅频特性是比较稳定的。

图8 移相器的等值电路

图9 移相器的幅频特性和相频特性

图10 罗氏线圈电流互感器的电路模型

图11 基于罗氏线圈的电流互感器的频率特性
3 积分器参数的优化
电子式电流互感器是智能变电站测量和保护等其他高级应用测试信号的来源,继电保护系统研究的侧重点是电力系统故障后的暂态过程,所以必须分析互感器模型的暂态响应是否可以满足保护系统的要求。
a. 电力系统发生故障时,通常故障电流包含有稳态电流、衰减交流及衰减直流分量,现以i(t)=e-t/0.1-cos100πt-e-t/0.2sin(200πt)作为输入电流,通过Matlab中的simulink建立数学模型,仿真分析互感器模型对故障电流的跟随特性,如图12所示。由仿真结果可见,该互感器模型能够反映原故障电流信号,不会发生波形畸变。

图12 互感器对故障电流的跟随特性曲线
b. 继电保护中常需要测量比正常电流值或者故障电流值大很多倍的电流,例如雷击电流。现模拟8/20 μs的雷击电流,将其作为罗氏线圈电流互感器的输入信号,仿真雷击电流的输出波形,结果如图13所示。从图13中的输出波形可以看出互感器对雷击电流的测量并不理想,波形发生畸变且出现时间延迟的现象。
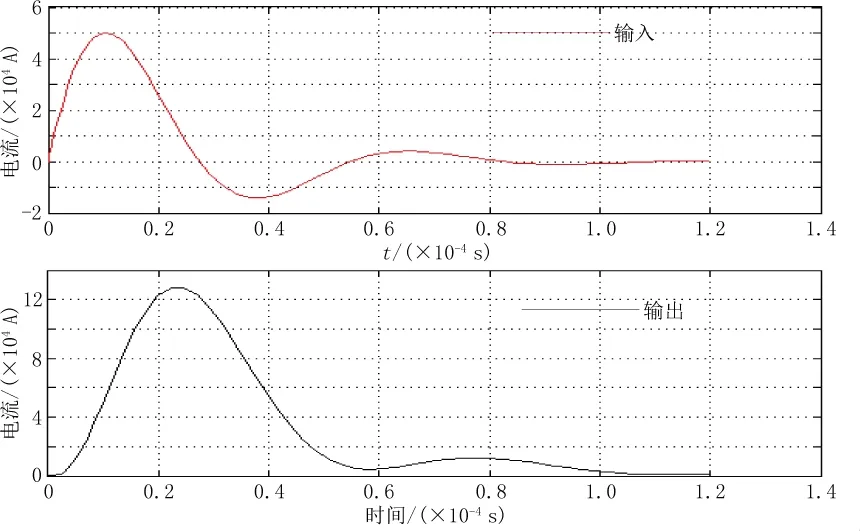
图13 互感器测量雷击电流的波形
由于罗氏线圈电流互感器测量的线性度和频率特性很大程度上决定于积分电路,因此对其积分电路进行分析,对无源-有源级联积分器参数进行调整。仍然以8/20 μs的雷击电流作为输入信号,只改变积分电路的单一参数,其他参数保持不变,仿真分析各个参数变化是对雷击电流波形的影响,结果如图14所示。从图14(a)-(d)分析得出:改变R1,R3,C1,C2都会引起电流波形显著变化,其中C2和R3的变化对低频段的影响较大,C1和R1的变化对高频段的影响较大,根据影响程度大小,改变参数值可解决电流波形恢复问题,为智能变电站高级应用提供精确的原始数据。
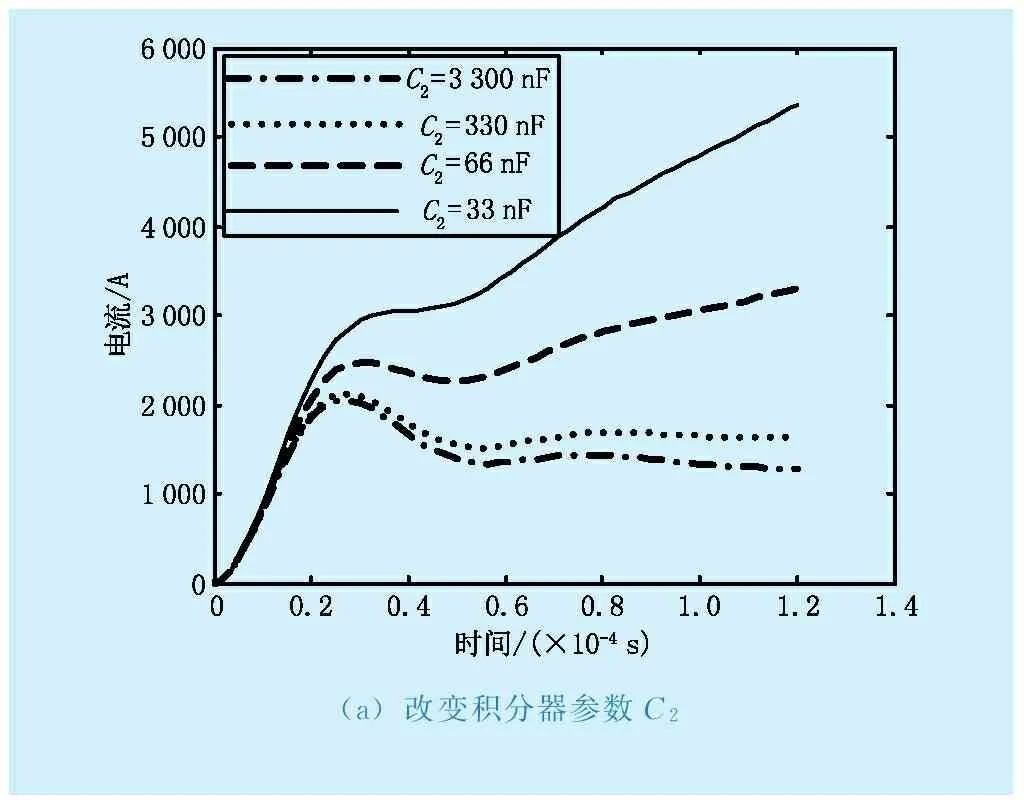
(a)改变积分器参数C2
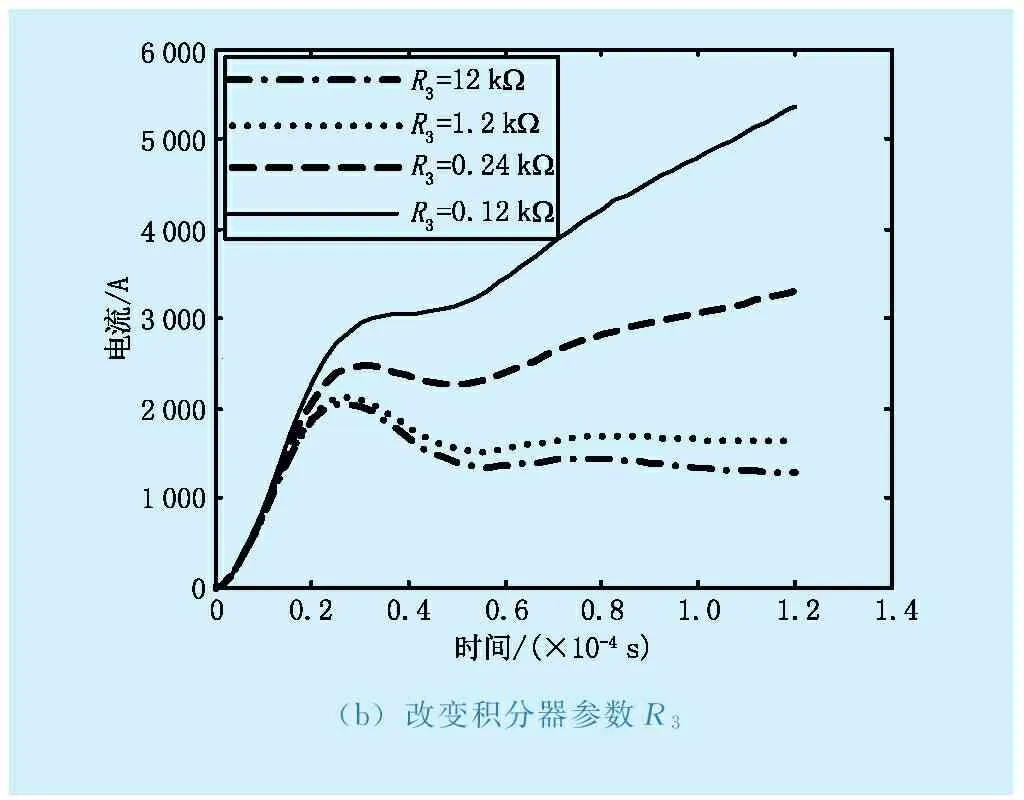
(b)改变积分器参数R3

(c)改变积分器参数C1

(d)改变积分器参数R1图14 改变积分器各参数的输出波形
对无源-有源级联积分电路参数进行改进,将R1=12 kΩ缩小1 000倍,其他参数保持不变。即:
R1=12 Ω;C1=33 nF;R2=20 MΩ;R3=1.2 kΩ;C2=330 nF。对修改过参数的级联积分器进行仿真,得到如图15所示的测量结果。由图15可以看出波形跟随效果良好,能够真实地反映雷击电流,说明参数优化的有效性。改进后的积分电路如图16所示,改变R1和C1具有相同的效果,但是选择改变R1的效果会更好,因为电阻的成本相对电容较低,且电阻受环境条件的影响程度相对电容也较小。

图15 修改积分器参数后互感器测量雷击电流的波形

图16 改进后的级联积分电路
4 结束语
本文主要研究罗氏线圈电子式互感器的工作原理,对罗氏线圈各主要工作单元(包括积分电路、低通滤波电路和移相电路)的传变特性进行仿真分析,利用Matlab中的simulink模块搭建罗氏线圈整体仿真模型,并对其传变特性进行分析,在此基础上提出了一种有源、无源级联积分器,通过仿真找到了积分器传变特性随元器件变化的规律,并对积分环节的元器件进行优化,提高了罗氏线圈对雷击电流传变的精确度。为互感器运用在故障电流和雷击测试的理论研究提供一定参考。
[1] 金世鑫,李 华,戴晓宇.电子式互感器的分类和原理综述[J]. 东北电力技术.2016,37(3):29-31.
[2] 周有庆,刘 琨,吴桂清,等.基于Rogowski线圈电子式电流互感器的研究[J].电力电气,2006,25(6):106-110.
[3] 张俊祥,刘立明,尹 明,等.电子互感器的数据还原技术研究[J].东北电力技术.2016,37(10):1-4,8.
[4] 李 伟, 尹项根, 陈德树,等.基于Rogowski线圈的电子式电流互感器暂态特性研究[J].电力自动化设备, 2008,28(10):34-37.
[5] 王宝诚, 王德玉, 邬伟扬.罗氏线圈的频率特性分析与传感器的设计方法[J].电工技术学报, 2009, 24(9):21-27.
