基于循环寻优的模块化多电平换流器模型预测控制
2018-03-21葛得初
张 虹, 葛得初, 白 洋
(东北电力大学电气工程学院, 吉林省 吉林市 132012)
1 引言
随着输电技术的不断发展,柔性直流输电在世界范围内得到广泛的关注和研究,而模块化多电平换流器(Modular Multilevel Converter,MMC)又是柔性直流输电技术领域中新的应用[1-4]。模块化多电平换流器作为一种新型电压源变换器,相比较于传统两电平或三电平拓扑结构的电压源换流器,其优点体现在模块化冗余设计,波形质量高,电压等级提高和故障处理能力强等方面[5-9],因此,基于MMC的高压直流输电系统成为柔性直流输电领域的研究热门。
尽管MMC具有诸多技术上的优势,但由于其拓扑结构的特殊性,导致交流侧相电流控制、子模块电容均压控制以及各相桥臂之间环流抑制成为其应用中亟需解决的问题。各独立子模块电容电压的不平衡与相间环流的存在都会影响系统运行的稳定性和安全性。如何把效果较好的控制方法合理地应用于MMC-HVDC系统中仍然值得深入讨论。现有针对MMC的控制方法大多基于经典控制理论进行设计,多采用PI控制器,其结构虽然简单,但控制过程调节时间过长[10],且控制器参数依赖于精确的系统模型而不易整定,不利于系统长期运行使用,所以在一定程度上限制了其应用。文献[11]采用基于两相静止坐标变换的控制策略,该策略避免了两相旋转坐标系统中的电流交叉耦合项,不需前馈解耦,通过双闭环控制器实现电容电压均衡和环流抑制,控制系统更加简单,但其无法避免因控制器参数众多而较难整定的问题。文献[12-15]都是通过坐标变换和解耦控制实现抑制环流与电容电压平衡,在控制器设计过程中,过度依赖模型精度,使得系统对控制器参数敏感,而且鲁棒性差,响应速度慢。
相比于经典控制理论,MMC的模型预测控制是基于目标函数的最优控制,通过目标函数可同时控制多个系统变量,对系统中未建模的非线性和不确定因素也有一定的适应性,具有建模直观、动态响应快、鲁棒性好等优势[16]。由于MMC桥臂子模块数众多,子模块数目的增加势必增加开关状态,模型预测控制(Model Predictive Control,MPC)算法运行时间和控制周期也将随之增加,这也是现有MPC控制策略中需要解决的问题。文献[17]提出一种状态分区的MPC预测方法,该方法能够显著降低计算量、减少运行时长,不足之处是该算法会对MPC部分控制性能造成影响。文献[18]针对级联型H桥逆变器的模型预测控制,虽然获得了较理想的控制效果,但计算过程相对复杂。传统的MPC控制通过计算所有开关状态组合以实现最优控制目标,随着桥臂串联的子模块数增多,计算量呈几何级数增长,无法满足运行效率和控制效果的双重要求,严重制约MPC工程推广应用。此外,传统MMC的MPC控制通常在一个目标函数下包含了电容电压平衡、环流抑制等多个子目标函数,在控制设计时还需考虑权重因子的选取,很难同时实现多个控制目标的最优控制[19]。
本文提出了一种循环寻优的MMC模型预测控制,针对MMC中所存在的不同目标函数,单独进行设计,逐级实现优化控制目标,无需考虑权重因子,且不需参数整定。即每一个控制周期内,在交流侧相电流控制的基础上,对其存在的误差,在环流抑制环节中进行补偿与修正,求得桥臂投入子模块数最优解,进一步平衡子模块电容电压,并利用相邻控制周期子模块数目变化量对桥臂子模块开关状态进行修正,以此优化开关频率,降低开关损耗。在Matlab/Simulink软件中搭建了MMC-HVDC仿真模型,验证所提控制策略的可行性和有效性。
2 MMC拓扑结构与数学模型
图1为MMC的等效电路。MMC换流器的两侧分别与交流电网和直流线路连接,Usk和isk(k=a,b,c)分别为交流侧电压和电流,L为桥臂串联电感,R用来等效桥臂的损耗,Udc和Idc分别为直流电压和直流电流,桥臂电压可以用6个受控电压源upk和unk(k=a,b,c)来等效,相应的桥臂电流分别为ipk和ink,其中下标p和n分别表示上桥臂和下桥臂,参考方向如图1所示。

图1 MMC等效电路图Fig.1 Equivalent circuit diagram of MMC
根据参考文献[20],桥臂电流表达式为:
(1)
(2)
式中,idiffk为同时流过上、下桥臂的换流器内部电流,称为k相内部不平衡电流,且有:
(3)
式中,izk(k=a,b,c)为桥臂内部环流。
这样,MMC的数学模型可以用以下两个方程来描述:
(4)
(5)
一般将式(4)称为外部特性方程,将式(5)称为内部特性方程。
在式(4)中,不妨设:
(6)
式中,uk为第k相的内部电动势。
3 循环寻优控制策略
3.1 交流相电流跟踪
设控制周期为Ts,将式(4)进行差分近似,得到离散化形式为:
(7)
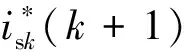
(8)
对于一个N+1电平的MMC换流器,理论上,在不考虑波动的情况下,各子模块电容电压均为Udc/N。因此,式(6)可改写为:
(9)
式中,Spki和Snki分别为k相上、下桥臂第i个子模块开关函数,取1、0分别代表该子模块处于投入、切除状态。
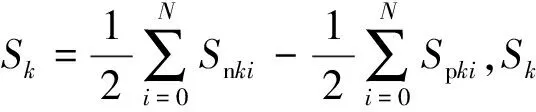
(10)
由于上、下桥臂开关状态和为0~N之间的数,所以Sk开关状态为:-N/2,-(N-2)/2,…,0,…,(N-2)/2,N/2,共N+1种可能,即uk取值有N+1种可能,则可知电流预测值和目标函数的计算次数均为N+1次。
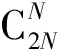
3.2 相间环流抑制
3.2.1 桥臂误差电压分析
在式(5)中令左边为:
(11)
式中,Udiffk为第k相的内部不平衡电压降。结合图1和基尔霍夫电压定律可知,Udiffk实际表示第k相内部不平衡电流idiffk在一个桥臂串联电抗上的电压降。
根据式(4)、式(5)和式(11),可推导出上、下桥臂电压实际值为:
(12)
(13)
即上、下桥臂电压实际值与交流电流控制中上、下桥臂参考电压存在误差电压Udiffk。
由式(12)和式(13)可得到:
uk_leg=upk+unk=Udc-2Udiffk
(14)
式中,uk_leg为第k相桥臂总电压。
由式(14)进一步可推知内部不平衡电压Udiffk是由于各相上、下桥臂的电压之和与直流电压不相等而引起的。需要指出的是,由于桥臂子模块电压存在波动,误差电压Udiffk存在正负之分。文献[21]指出各相上、下桥臂电压之和彼此不一致将产生内部环流izk。若环流在MMC三相桥臂中不加控制地流动,势必会使桥臂电流产生较大的波动,从而发生畸变,还会增加额外的功率损耗,所以需采取一定的方法抑制环流izk。
此外,随着电压等级和输出电平数的提高,桥臂串联子模块数随之增加,每相桥臂与直流侧的误差电压逐渐增大,在导致环流增大的同时,也会使子模块电容电压产生较大波动。
综上分析,由于存在电压误差,在相电流控制过程中所确定的模块数并不是最优的,使得遵循传统MPC算法的最优开关函数组合,在其实施于MMC换流器时已丧失了最优性,导致系统被控制量并不能达到理想状态,最终影响系统的控制性能。因此,有必要在环流抑制环节中对存在的误差进行补偿。
3.2.2 环流抑制策略
根据环流形成的机理,为抑制环流需减小各相桥臂上、下电压之和与直流侧电压的误差Udiffk。因此本文采用误差补偿法减小桥臂不平衡电压以达到抑制环流的目的,通过选择适当的模块(误差模块)进行投切降低桥臂误差电压水平,即以适当增加开关损耗为代价来达到减小误差的目的。具体控制方法如下:
(1)在每个控制周期实时检测误差电压。
(2)根据误差电压值的大小确定误差模块数目。
(3)根据误差电压的符号判断下一控制周期桥臂误差模块的投入与切除,若uk_leg>Udc,则从上、下桥臂投入运行的子模块中切除适当的子模块;若uk_leg (4)结合最近电平逼近调制策略与电容电压排序算法,并编写适当程序对子模块进行控制。 根据MMC换流器上、下桥臂对称性,需同时在上、下桥臂进行误差模块投切。误差模块的引入只起到了抑制换流器内部相间环流的作用,并不影响内部电动势uk的输出值,故不影响交流侧电流控制,对换流器外部输出特性并无影响。 在上、下桥臂引入误差模块后,上、下桥臂电压方程变为: (15) (16) 进而得到: (17) 式中,ncir为误差补偿模块的数目;vC为子模块电容电压。 由式(17)可知,采用电压补偿将会降低每相桥臂电压与直流侧电压误差,则每相内部不平衡电压减小,以获得抑制环流izk的效果。 引入误差补偿模块后,补偿电压为ncirvC,取补偿后的上、下桥臂电压作为模型预测控制的参考值: (18) (19) 对式(5)进行差分近似,得到离散化形式为: (20) 另外,补偿模块数目ncir可根据输电系统中桥臂误差电压水平确定,当MMC电平数较多时,ncir可进行扩展。本文研究采用ncir取值范围为-1,0,1。 由式(3)可知,内部不平衡电流idiffk包含两个分量,其中Idc/3为直流分量,只与系统传输功率有关,不可控制,izk为可控分量,即为环流,需将这一分量抑制为零,每相的内部不平衡电流应控制为Idc/3。因此,将idiffk参考值选为Idc/3,并据此设计最优化目标函数: (21) 式中,Idc(k+1)为直流侧预测电流,计算方法如下: 假设交流侧与直流侧之间功率传输没有损耗,则 Pac=Pdc=UdcIdc (22) (23) 因此,目标函数修改为: (24) 在环流抑制阶段中,该算法以前一时刻交流电流控制中换流器存在的误差补偿当前时刻预测值的输出,从而实现对误差的在线补偿,得到修正后的开关组合状态。通过计算得到上、下桥臂参考电压后,再分别计算各个误差补偿模块下的目标函数gdiffk的值,选取gdiffk最小值所对应的ncir,在此过程中所需计算的目标函数次数仅为3次。由以上分析可知,该控制策略显著降低了目标函数的计算量。 子模块电容电压由开关状态和桥臂电流决定,通过环流抑制得到上、下桥臂参考电压分别为式(18)、式(19),即等于补偿后的桥臂电压,子模块电容电压参考值为Udc/N,则每个桥臂投入的子模块数为: (25) (26) 子模块处于投入状态时电容电压表达式为: 对比式(1)与式(7)可知,修正后的比例谐振控制器相比于理想的比例谐振控制器多增加了一个参数ωc用于调整控制器基波频率附近的增益和带宽,由式(7)可以看出系统性能由Kp、KR以及ωc共同决定。选修正后的比例谐振控制器参数为:ωc=5,Kp=1,KR=100,该参数下的控制器Bode图如图3~图5所示。图中可以看出,在基波频率处系统增益为40 dB,完全可以实现对输入电流指令的无静差跟踪。同时具有很好的稳态裕度和暂态性能[10]。 (27) 子模块处于切除状态时电容电压表达式为: Udci(k+1)=Udci(k) (28) 式中,i=1,2,…,N;im(k)为k时刻子模块所在桥臂的电流测量值;Udci(k+1)为下一周期电容电压预测值。 传统MPC目标函数为: (29) 本文选择其中一个子模块,重新定义目标函数: (30) 由式(27)、式(28)可知,子模块处于充电状态或放电状态会影响目标函数的取值,当处于充电状态时,将选择目标函数的最小值,当处于放电状态时,将选择目标函数最大值。因此,将目标函数修改为: (31) 其中,充电时imTs/C>0,放电时imTs/C<0。目标函数修改之后,无论子模块处于充电状态还是放电状态,都选取目标函数最小值。 (32) 式中,SMpk_ONold和SMnk_ONold为k时刻上、下投入运行模块数;SMpk_ONnew和SMnk_ONnew为k+1时刻上、下桥臂更新的子模块数。 为降低开关切换频率,已投入运行状态的SM在下一个周期内保持不变,当ΔSMpk_ON>0时,从处于切除状态的SM中,选取ΔSMpk_ON个模块投入运行,根据式(31),应选取gVdc值最小的SM,此时需计算目标函数的次数为N-ΔSMpk_ON;当ΔSMpk_ON<0时,从已投入的SM中选取ΔSMpk_ON个模块切除,但此时根据式(31),将选取gVdc值最大的模块,需计算目标函数的次数为SMpk_ON,下桥臂控制过程与上桥臂相同。在开关频率优化过程中,开关切换次数减少到ΔSMpk_ON和ΔSMnk_ON,开关频率显著降低,在此阶段中,目标函数计算次数约为N次。采用开关频率优化控制后电容电压控制框图如图2所示。 表1为11电平下MMC传统MPC控制策略与本文控制策略所考虑的开关状态组合数目对比。对于传统MPC控制算法,计算的状态数目共为184756,而本文算法将状态数目降低到44,计算量降低了约99.97%,提高了算法的运行效率,且随着桥臂级联子模块数目增多,该算法降低计算量的优势更加明显。 图2 SM电压平衡和开关频率优化MPC控制框图Fig.2 MPC control block diagram of SM voltage balancing and switching frequency optimization 算法交流侧电流控制相间环流抑制SM电容电压平衡控制总数循环寻优算法1130~3014~44传统MPC算法184756184756 为了验证本文控制策略的有效性,利用Matlab/Simulink软件平台搭建了如图3所示的三相MMC-HVDC背靠背系统仿真模型。其中换流站MMC1采用定直流电压和无功功率控制方式,MMC2采用定有功功率和无功功率控制方式,仿真系统参数如表2所示。 图3 MMC-HVDC系统结构示意图Fig.3 Schematic diagram of MMC-HVDC system structure 参数数值有功功率/MW24交流系统电压/kV8直流电压/kV20频率/Hz50桥臂电感/H002桥臂电阻/Ω002桥臂子模块数10子模块电容/F0002子模块额定电压/V2000采样周期/μs20 在稳态运行时,通过控制功率在两个换流站之间双向流动,验证本文控制策略的控制效果。图4为应用本文所提MPC控制策略,基于功率在两个换流站之间双向流动时系统各电气量的仿真波形图。子模块数取N=10,00.2s时间内,功率从换流站1流向换流站2,0.2s时刻施加控制信号,使功率反向流动,0.20.3s时间内,为暂态过渡阶段,0.3s时刻,完成功率反向流动,仿真时间持续0.5s。 由图4(a)和图4(b)可知,稳态时系统电压和交流电流保持稳定,在功率反向流动的暂态过渡期间内,三相交流电压、电流平稳变化,未产生过大波动,交流侧有较好的输出。图4(c)和图4(d)为系统的有功功率和无功功率变化曲线,可以看出,在功率换向期间内,能够实现有功功率平稳过渡,而无功功率波动很小,由于采用定无功功率控制方式,无功功率始终保持在0。图4(e)为直流线路中电流,可以看出,电流较稳定,其误差控制在额定电流的8%以内,满足要求。图4(f)为换流器MMC1内部不平衡电流idiffk(以a相为例)波形图,可以看出,在仿真过程中,内部不平衡电流始终控制在Idc/3附近,很好地验证了本文提出的环流抑制策略。图4(g)为换流器MMC1内部环流izk(以a相为例)波形,可以看出,环流很小,其抑制效果明显,而且在暂态过渡期间内,环流未出现波动,与本文所提出的控制策略吻合。图4(h)为上、下桥臂子模块电容电压(以a相为例)波形图,可以看出,电容电压幅值波动较小,均不超过其额定值6%,电容电压平衡效果明显。 图4 采用本文控制策略系统各电气量仿真波形图Fig.4 Simulation of system parameters under control strategy in this paper 图5 传统MPC控制策略与本文控制策略仿真波形比较Fig.5 Simulation comparison between traditional MPC control strategy and control strategy in this paper 为验证本文控制策略的有效性,对传统MPC控制策略与本文所提控制策略进行动态性能测试比较,基于11电平MMC-HVDC背靠背仿真系统,功率单向流动,方向为从MMC1流向MMC2,交、直流侧电流参考值分别为200A和120A,有功功率参考值为2.4MW,0.4s时刻,MMC1交流侧A相发生单相接地短路故障,两种策略下仿真结果如图5所示。 在发生接地故障后,交流电压产生严重跌落;比较图5中两种策略下交流电流,本文策略交流电流控制与追踪能力明显优于传统MPC策略,交流电流波动减小,波形较稳定;对比功率变化曲线可知,本文策略能有效抑制故障发生后的功率波动;直流线路电流在发生单相接地故障后,电流产生较大波动,而采用本文方法后,波动量降低,满足误差要求;传统MPC控制下,故障后环流值增大且产生过大波动,本文方法下环流始终维持在0值附近,波形较平稳;从故障相上、下桥臂子模块电容电压可以看出,由于交流侧故障电流的馈入,电容电压偏离其额定值较严重,而本文方法中,在已经取得良好效果的交流电流控制与环流抑制基础上,其SM电压平衡策略也能发挥较好的平衡电压目的,SM电压始终保持在较稳定水平,未产生较大波动,控制效果明显。 为验证本文策略能够适应MMC灵活可拓展特性,分析了桥臂子模块数增加的情况下该控制策略对环流抑制效果,针对N=10,20,30时分别进行仿真分析,仿真波形如图6所示。由于在子模块数增加时,可根据系统电压水平对误差电压补偿模块数进行扩展,因而误差电压会显著降低,环流抑制效果更好。从图6可以看出,随着串联子模块数目增加,桥臂相间环流仍然保持在很低的水平,与本文所述理论相符。 图6 N=10,20,30时系统环流仿真波形Fig.6 Simulation of system circulating current for N=10, 20, 30 本文还分析了所提控制策略下的开关频率和开关损耗。以MMC1 a相上桥臂SM1为研究对象,图7为子模块PWM仿真结果,其中favg为子模块平均开关频率。图7(a)为目标函数式(31)下的PWM仿真结果,未考虑开关频率优化,可以看出,在不优化开关频率的情况下,子模块平均开关频率很高。作为比较,图7(b)为在电容电压平衡基础上考虑开关优化,即在目标函数式(31)基础上将式(32)纳入考虑的仿真结果,结果表明子模块平均开关频率明显降低。 图7 门极信号仿真结果比较Fig.7 Simulation comparison results of gate signal 图8为子模块中IGBT(以a相SM1为例)的平均损耗。其中,T1和T2为子模块中的IGBT,D1和D2为所对应的二极管,Pon为通态损耗,Psw为开关损耗,Prr为二极管反向恢复损耗,IGBT具体参数和功率损耗计算方法由文献[21]给出。可知,采用开关优化策略前后,通态损耗几乎相同,但是在采用开关优化策略之后,由于开关频率的降低,IGBT的开关损耗和二极管的反向恢复损耗明显减少。 图8 IGBT和二极管平均功率损耗Fig.8 Average power loss of IGBT and diode 本文提出一种循环寻优的模型预测控制算法,通过分析交流电流控制过程中桥臂参考电压误差,在环流抑制环节中引入误差模块以抵偿桥臂误差电压,对交流电流控制阶段中得到的开关组合状态进行修正,进而在此基础上实现平衡子模块电容电压与优化开关频率,在每个控制周期不断重复上述过程,从而达到在线循环寻优的目的,提高控制精度。在Matlab/Simulink中搭建了仿真模型,对仿真结果进行分析,仿真结果表明本文控制策略有如下特点: (1)相比于传统MPC控制方法,本文设计在每个桥臂中仅增加一个模块开关损耗的情况下,实现对MPC算法中参考电压的修正,以适当增加开关损耗为代价来提高控制目标精度,并且同时能够降低算法计算量,提高运行速率。 (2)在随电平数增加子模块数增多的情况下,该控制策略仍然保持了良好的环流抑制能力,可满足电压等级高、输送容量大的特点,增加了系统运行可靠性,符合MMC灵活可拓展特性,有利于在今后工程实际中扩展应用。 (3)与以往方式不同的是,本文通过修正量对开关状态进行修正以优化开关频率,能够有效降低开关切换频率,进而降低运行过程中开关损耗,延长开关使用寿命。在实际应用过程中,经济性较高。 [1] 朱晋, 韦统振, 霍群海, 等 (Zhu Jin, Wei Tongzhen, Huo Qunhai, et al.). 适用于架空线的MMC-HVDC换流站子单元拓扑系列 (A series of sub-module topology suitable for overhead lines MMC-HVDC) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2015, 34(2): 20-24. [2] Beddard A, Barnes M. Modelling of MMC-HVDC systems-An overview [J]. Energy Procedia, 2015, 80: 201-212. [3] 董云龙, 凌卫家, 田杰, 等 (Dong Yunlong, Ling Jiawei, Tian Jie, et al.). 舟山多端柔性直流输电控制保护系统 (Control & protection system for Zhoushan multi-terminal VSC-HVDC) [J].电力自动化设备(Electric Power Automation Equipment), 2016, 36(7): 1-7. [4] 肖亮, 徐政, 刘昇, 等 (Xiao Liang, Xu Zheng, Liu Sheng, et al.). 向无源网络供电的MMC-HVDC送端交流故障穿越策略 (AC fault ride-through strategy of MMC-HVDC connected to passive networks) [J]. 电工技术学报 (Transactions of China Electrotechnical Society), 2016, 31(15): 89-98. [5] Saeedifard M, Iravani R. Dynamic performance of a modular multilevel back-to-back HVDC system [J]. IEEE Transactions on Power Delivery, 2010, 25(4): 2903-2912. [6] 韦延方, 郑征, 王晓卫 (Wei Yanfang, Zheng Zheng, Wang Xiaowei). 柔性直流输电系统稳态潮流建模与仿真 (Model and simulation of steady state power flow in a flexible HVDC transmission system) [M]. 北京: 科学出版社 (Beijing: Science Press), 2015. [7] 许彬, 王平, 李子欣, 等 (Xu Bin, Wang Ping, Li Zixin, et al.). 模块化多电平换流器阀段运行试验方法研究 (Research on operational test method for modular multi-level converter valves) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2016, 35(7): 24-30. [8] 罗永捷, 李耀华, 李子欣, 等 (Luo Yongjie, Li Yaohua, Li Zixin, et al.). 多端柔性直流输电系统直流故障保护策略 (DC short-circuit fault protection strategy of multiterminal-HVDC systems) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2015, 34(12): 1-6. [9] 王秀丽, 郭静丽, 庞辉, 等 (Wang Xiuli, Guo Jingli, Pang Hui, et al.). 模块化多电平换流器的结构可靠性分析 (Structural reliability analysis of modular multilevel converters) [J]. 中国电机工程学报 (Proceeding of the CSEE), 2016, 36(7): 1908-1914. [10] 朱玲, 符晓巍, 胡晓波, 等 (Zhu Ling, Fu Xiaowei, Hu Xiaobo, et al.). 模块化多电平变流器HVDC系统的模型预测控制 (Model predictive control of modular multilevel converter for HVDC system) [J]. 电力系统保护与控制 (Power System Protection and Control), 2014, 42(16): 1-8. [11] 孙一莹, 赵成勇, 赵静, 等 (Sun Yiying, Zhao Chengyong, Zhao Jing, et al.). 基于两相静止坐标系的MMC-HVDC系统稳态控制策略 (A steady-state control strategy of MMC-HVDC transmission system based on two-phase stationary reference frame) [J]. 电网技术 (Power System Technology), 2013, 37(5): 1384-1388. [12] Mishra Richa, Shukla Anshuman. A proportional resonator-based control scheme to suppress AC components in circulating current of modulator multilevel converter [A]. IECON 2013 - 39th Annual Conference of the IEEE Industrial Electronics Society [C]. 2013. 6170-6175. [13] 褚衍超, 黄守道, 孔凡蓬, 等 (Chu Yanchao, Huang Shoudao, Kong Fanpeng, et al.). 基于内模控制器的MMC-HVDC稳态控制 (Steady state control of MMC-HVDC system based on internal model controller) [J]. 电网技术 (Power System Technology), 2015, 39(8): 2223-2229. [14] Bahrani B, Debnath S, Saeedifard M. Circulating current suppression of the modular multilevel converter in a double-frequency rotating reference frame [J]. IEEE Transactions on Power Electronics, 2016, 31(1): 783-792. [15] Lizana R, Perez M A, Bernet S, et al. Control of arm capacitor voltages in modular multilevel converters [J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1774-1784. [16] 梁营玉, 张涛, 刘建政, 等 (Liang Yingyu, Zhang Tao, Liu Jianzheng, et al.). 模型预测控制在MMC-HVDC中的应用 (The applications of the model predictive control of MMC-HVDC) [J]. 电工技术学报(Transactions of China Electrotechnical Society), 2016, 31(1): 128-138. [17] Zhang Y, Lin H. Simplified model predictive current control method of voltage-source inverter [A]. 2011 IEEE 8th International Conference on Power Electronics and ECCE Asia (ICPE & ECCE) [C]. 2011. 1726-1733. [18] Cortés P, Wilson A, Kouro S, et al. Model predictive control of multilevel cascaded H-Bridge inverters [J]. IEEE Transactions on Industrial Electronics, 2010, 57(8): 2691-2699. [19] Vatani M, Bahrani B, Saeedifard M, et al. Indirect finite control set model predictive control of modular multilevel converters [J]. IEEE Transactions on Smart Grid, 2015, 6(3): 1520-1529. [20] 徐政 (Xu Zheng). 柔性直流输电系统 (Flexible direct current transmission system) [M]. 北京: 机械工业出版社 (Beijing: China Machine Press), 2012. [21] Freytes J, Gruson F, Delarue P, et al. Losses estimation method by simulation for the modular multilevel converter [A]. 2015 IEEE Electrical Power and Energy Conference (EPEC) [C]. 2015. 332-338.3.3 电容电压平衡与开关频率优化控制策略
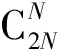
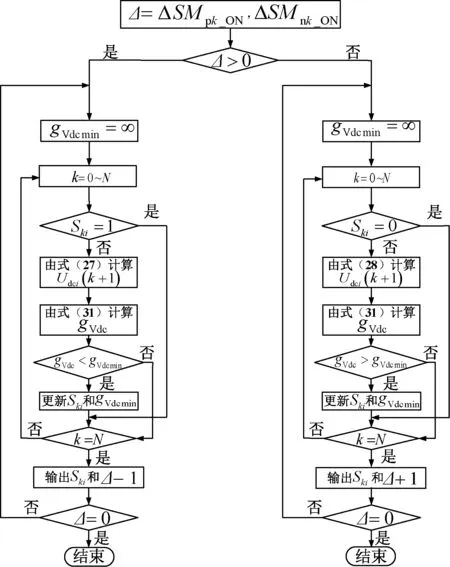
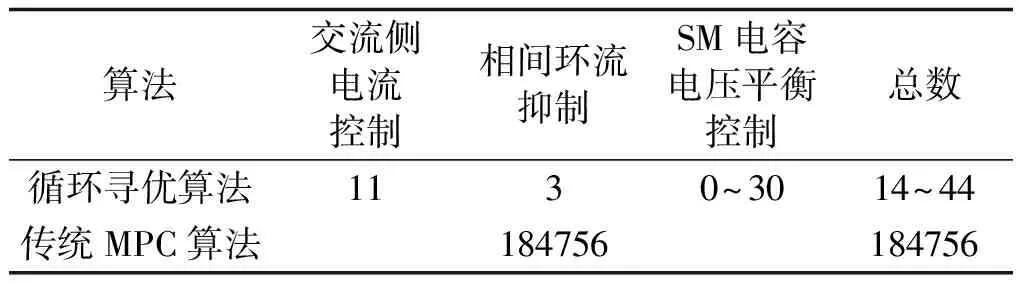
4 仿真分析
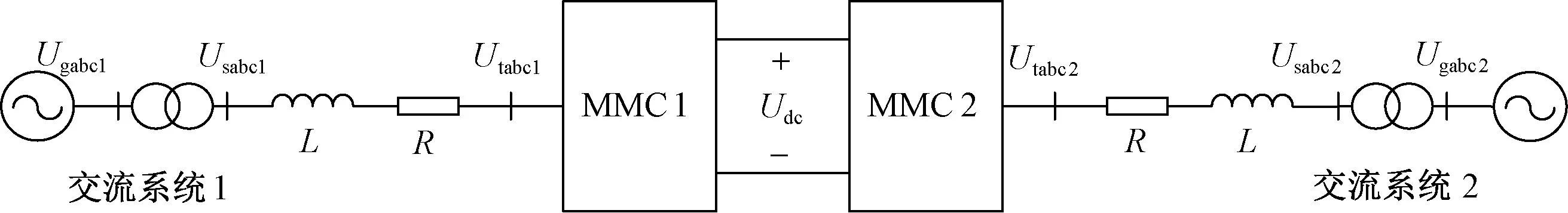
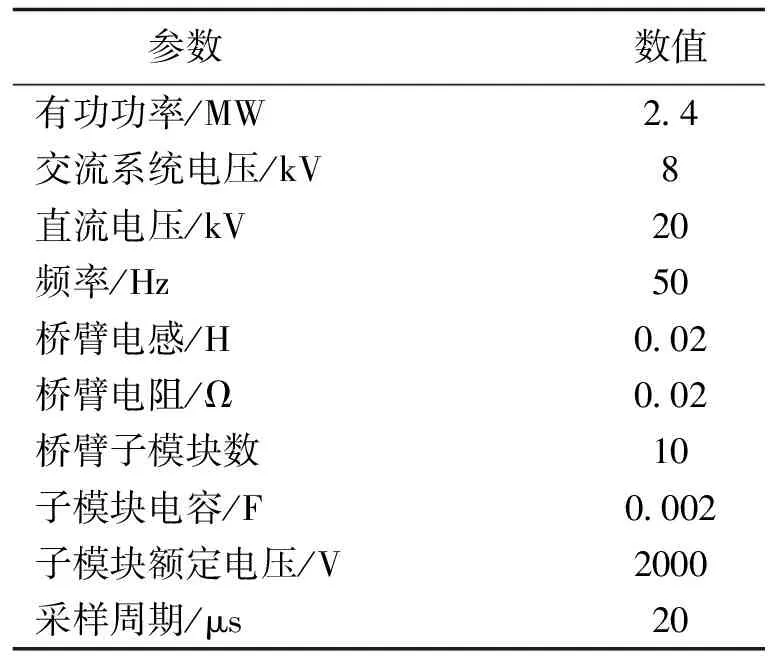
4.1 稳态性能
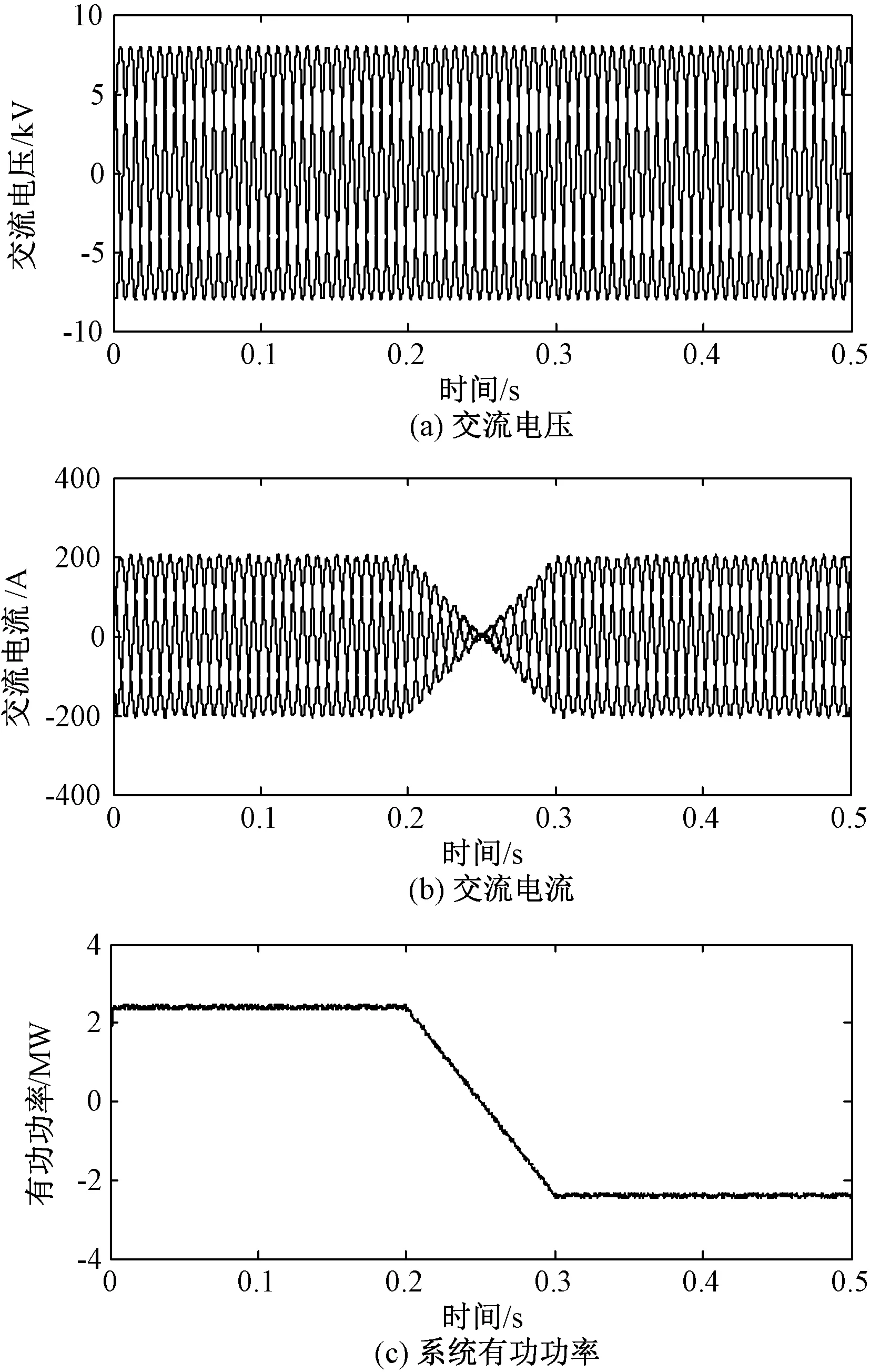

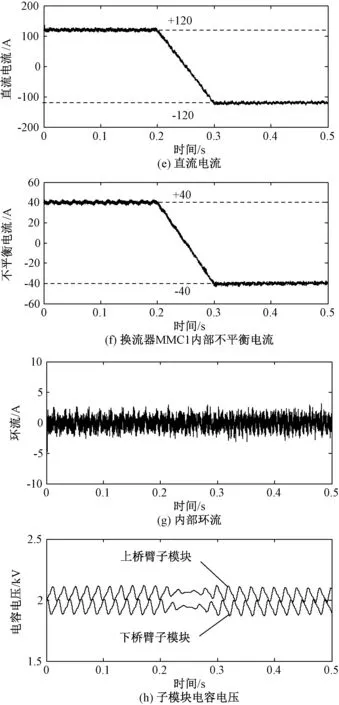
4.2 动态性能
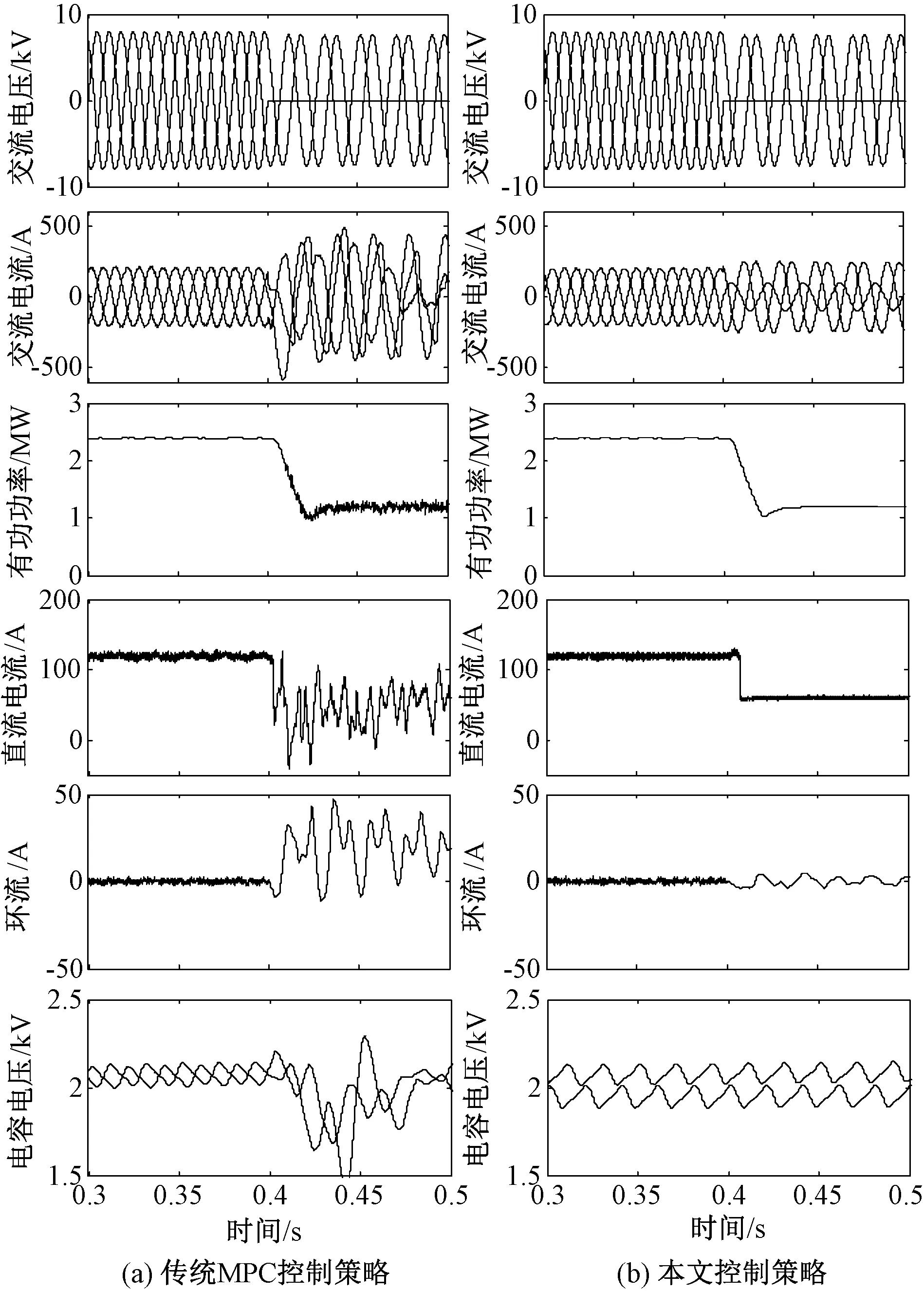
4.3 拓展特性
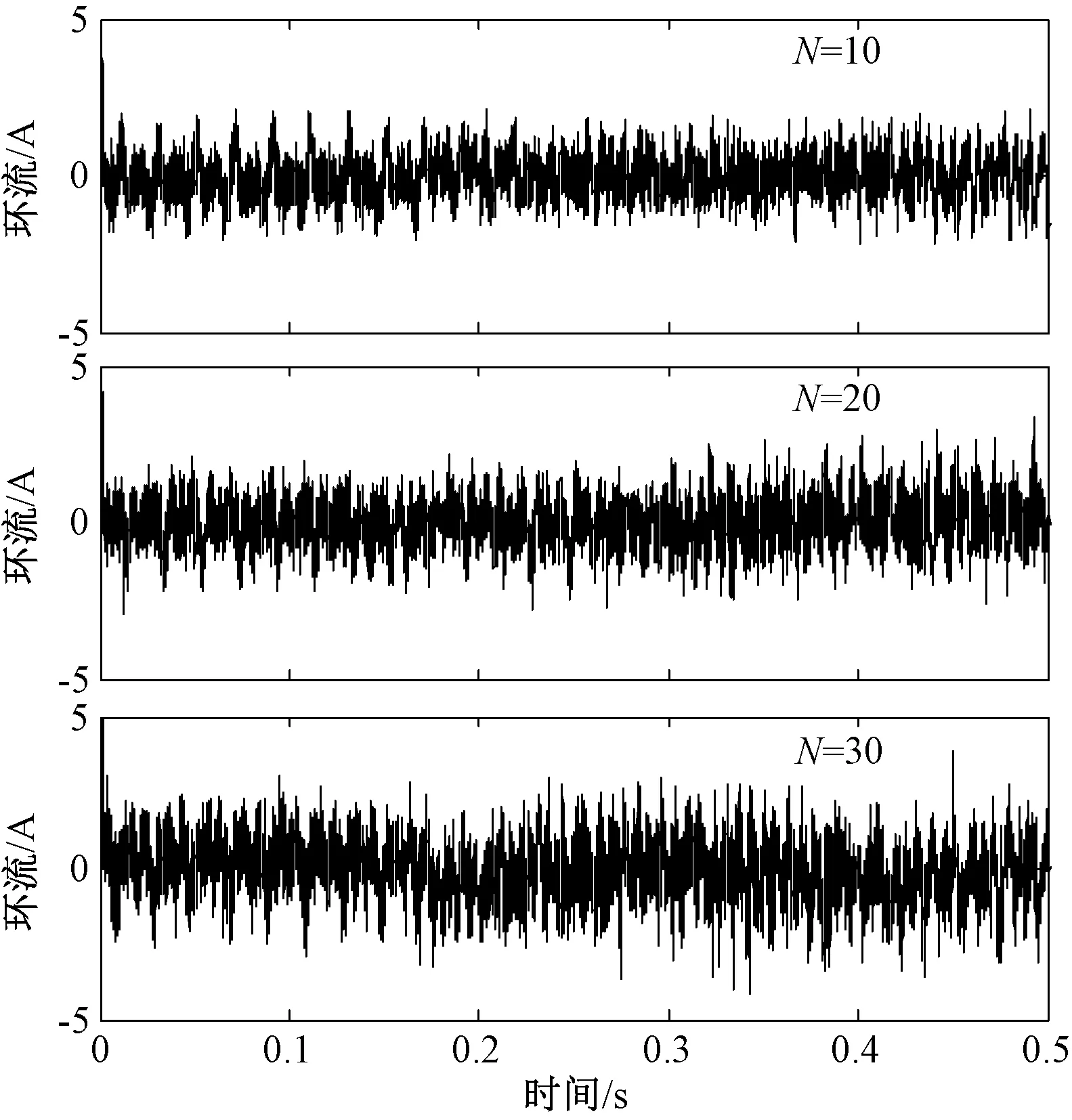
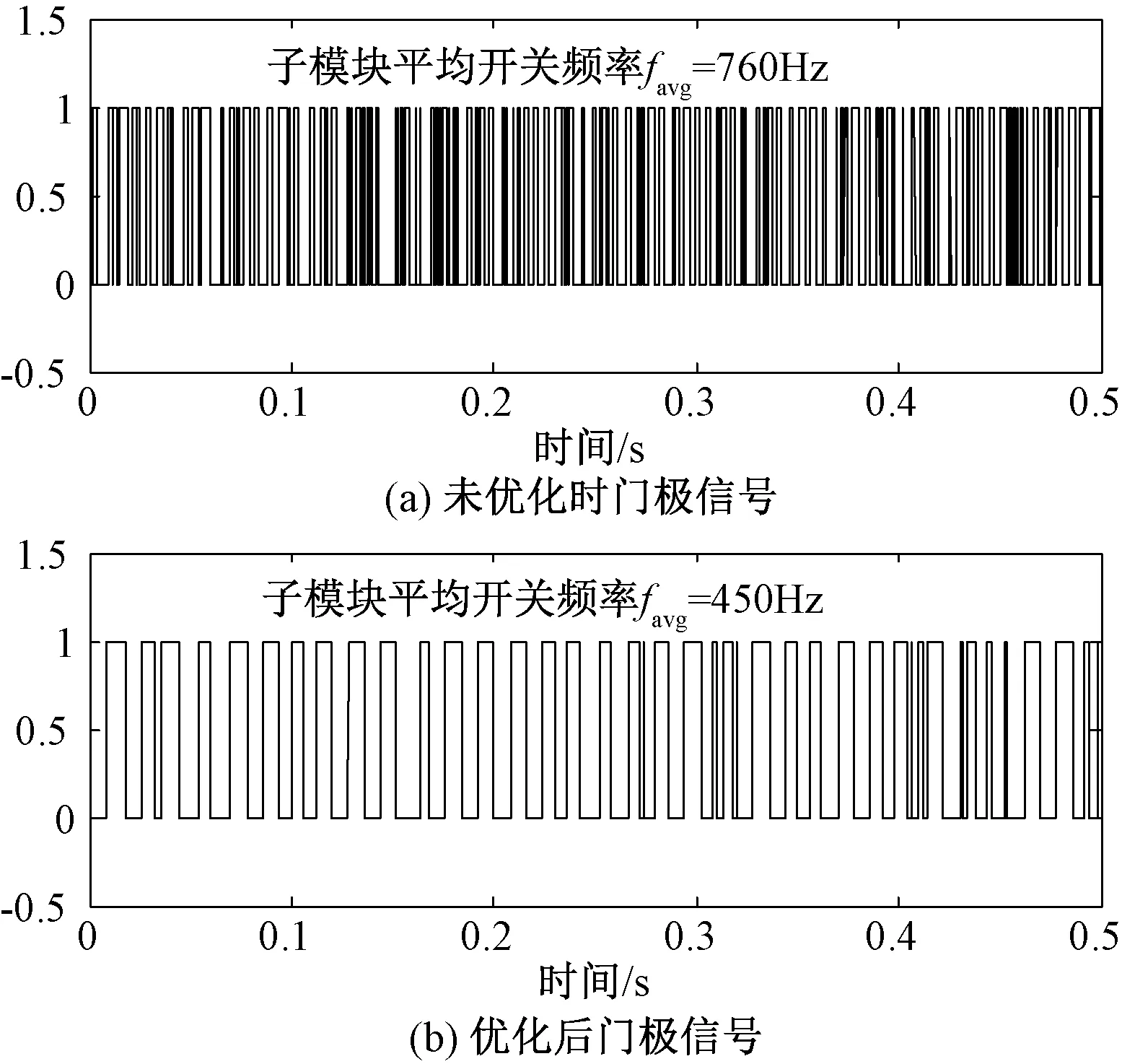
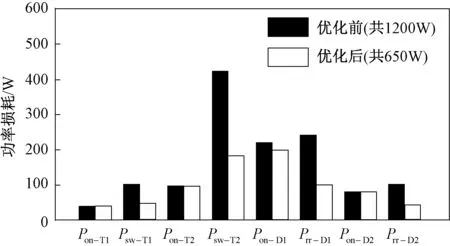
4.4 开关频率优化与损耗
5 结论
