平抑风电出力波动的混合储能系统优化策略
2018-03-21孙春顺杨江涛韩立哲粟咏梅
刘 佳, 孙春顺, 杨江涛, 韩立哲, 粟咏梅, 胡 宸
(1. 长沙理工大学 电气与信息工程学院,湖南 长沙 410114;2. 国网湖南省电力公司 检修公司,湖南 长沙 410007)
0 引言
化石能源危机与环境污染问题,使得人类对可再生能源[1]的关注与日俱增。其中风能因其清洁、产量丰富,而具有极大的开发价值。但风电出力通常具有较大的波动性,如其直接并网,将对电能质量产生影响[2]。针对风电出力的故有特点,有学者提出采用储能装置来实现风能对电网的友好接入[3],使风能得到更好的发展。
储能装置与风电的结合,将使风电出力波动得到有效改善[4]。传统处理中,根据蓄电池能量密度大,循环充放电时间长[5]的特点,采取蓄电池单独进行作用。但风电出力随机性会造成蓄电池频繁充放电,影响其使用寿命。而实际风电波动频繁部分往往能量相对较小,单独采用蓄电池显然不够合理。而超级电容功率密度大,响应快速,循环充放电次数多[6]的特点与风电波动高频部分相适应,故而采用超级电容与蓄电池相结合的混合储能系统在平抑风电出力波动方面将拥有更大的优势。
现阶段储能装置的造价相对高昂,故制定有效的控制策略和配置合理的储能装置容量[7,8]将是平抑风电出力波动的重要内容。文献[9]在不影响蓄电池使用寿命的前提下采取超前处理手段延长超级电容的寿命;文献[10]利用随机规划建立混合储能经济模型,并以二者的荷电状态制定相应的模糊控制规则;文献[11]提出了一种滤波时间常数根据电池荷电状态及风电出力自动调节的控制策略;文献[12]在文献[11]的基础上将风电功率改为风电功率预测偏差;文献[13]提出协调蓄电池与超级电容的功率分配策略,并以系统年综合成本最小为目标建立模型。
上述文献采取了较多措施对功率波动进行平抑;但对于储能装置的保护,大多以延长单一储能设备寿命为方向。本文在上述讨论的基础上,同时计及影响超级电容和蓄电池使用寿命的决定因素,针对超级电容容量易达到极值的特点,利用预先处理对其输出功率进行修正,对于蓄电池则采取一种限值管理手段,避免其出现过充或过放。同时,建立以平均成本最小为目标的机会约束规划模型,合理配置超级电容和蓄电池的功率和容量。
1 风电功率平抑策略
风电出力具有波动性,并网之前必须加以适当的处理。其中风电出力波动中的高频部分可由超级电容补偿,低频部分则由蓄电池进行处理;而波动的剩余部分功率因其幅度不大,可直接由电网进行消纳[14]。
采取一阶低通滤波器对风电功率进行滤波得到目标功率;而二者之间的差值则由混合储能系统进行补偿,系统中超级电容和蓄电池的参考功率在后面进行了具体说明。
(1)
PHESS=Pw-Pw_ref
(2)
式中:Pw为风电实时功率;Pw_ref为风电出力的目标功率;TL为一阶低通滤波器的时间常数;PHESS为混合储能系统的参考功率。
2 混合储能系统功率分配策略
2.1 混合储能数学模型
混合储能系统实时功率吞吐是平抑风电出力波动的主要手段,其中储能装置的输出功率决定了波动平抑效果。除自身特性外,输出功率主要由储能装置剩余容量以及最大允许充放电功率决定[15]。为方便描述,将储能装置剩余容量与额定容量的比值定义为荷电状态(State of Charge,SOC)。以下为储能装置工作时剩余容量的关系式。
Ei(t)=(1-δsdi)Ei(t-1)+Pi(t)Δtηci
(3)
Ei(t)=(1-δsdi)Ei(t-1)+Pi(t)Δt/ηdi
(4)
SOCi(t)=Ei(t)/Ei_re
(5)
式中:Ei_re为储能装置的额定容量;i=sc,b分别代表超级电容和蓄电池;P(t)为t时刻的充放电功率;E(t-1)为前一时刻的剩余容量;δsd为储能装置的自放电率;ηc和ηd为储能装置的充电和放电效率;SOC(t)为t时刻的荷电状态;其范围处于SOCmin和SOCmax之间。
t时刻储能装置的充放电功率(充电为正,放电为负)如下所示。
Pi(t)=min{Pi_ref(t),Pi_Cmax(t)}
(6)
Pi(t)=-min{|Pi_ref(t)|,Pi_Dmax(t)}
(7)
式中:Pi_ref(t)为t时刻储能装置的参考功率,其计算在后面给出。Pi_Cmax(t)和Pi_Dmax(t)分别为t最大允许充电功率和放电功率,由当前剩余容量决定,具体关系式如下所示。
Pi_Cmax(t)=[SOCimaxEi_re-
(1-δsdi)Ei(t-1)]/ηciΔt
(8)
Pi_Dmax(t)=[(1-δsdi)Ei(t-1)-
SOCiminEi_re]ηdi/Δt
(9)
2.2 预先处理策略
传统混合储能功率分配中,在得到混合储能系统总的参考输出功率后,通常采用高通滤波器对参考功率进行分解,并采以相应的措施在超级电容和蓄电池之间进行功率分配[15]。但由于风电的随机性,在某一时段出现风电出力突变,如果超级电容在前一时段内荷电状态已趋于饱和,由于超级电容能量密度相对较小若不加适当处理则将会导致超级电容长时间处于极限状态(容量达到最大或最小),势必影响超级电容的使用寿命。
基于此,为防止超级电容长时间处于限值状态对其寿命造成的影响,本文采取一种预先处理策略,当某一时刻风电功率出现较大波动时,对超级电容进行提前充放电[9],将原本由超级电容提供的一部分功率转移到蓄电池,而蓄电池相对超级电容而言容量较大,适当的功率转移不会影响到蓄电池的正常运行。按此方式进行调整保证了混合储能最终的输出参考功率不发生改变,在延长超级电容使用寿命的同时不致对平抑效果产生影响。具体操作如图1所示。

图1 预先处理策略
由图1可得:
(10)
式中:Psc_ref0和Pb_ref0为未经预先处理时超级电容和蓄电池的参考功率;ΔPsc和ΔPb为预先处理时超级电容和蓄电池的转移功率;Psc_ref1和Pb_ref1为预先处理后超级电容和蓄电池的参考功率,且Psc_ref1为超级电容最终的参考补偿功率,即Psc_ref1=Psc_ref。TH为高通滤波器的时间常数。
若下一时段风电功率波动未出现显著变化,此时则无需采取预先处理措施,使超级电容和蓄电池按给定的参考功率进行补偿即可,即蓄电池和超级电容之间不需要进行功率转换。
ΔPsc(t)=ΔPb(t)=0
(11)
当风电出力出现显著的下降趋势时,则在前一时段对超级电容进行提前充电来应对下一时刻的出力突降,提前充电时段的功率由蓄电池放电补偿。
ΔPsc(t)=Psc_Cmax(t)-Psc_ref0(t)
(12)
当风电出力出现明显的上升趋势时,则在前一时段对超级电容进行提前放电来应对下一时刻的出力突增,提前放电时段的功率由蓄电池充电补偿。
ΔPsc(t)=-Psc_Dmax(t)-Psc_ref0(t)
(13)
2.3 蓄电池限值处理
上述讨论中,仅针对防止超级电容长期处于限值状态进行处理,而超级电容引入的主要目的是减少蓄电池单独作用时频繁充放电对其寿命的影响;此外,蓄电池的寿命还与过充和过放有关。为进一步延长蓄电池使用寿命,本文按荷电状态将蓄电池划分为3个区域,根据蓄电池所处的不同区间动态调整其参考补偿功率,保证蓄电池荷电状态不致到达极限值,从而避免出现过充或过放现象影响寿命。
蓄电池正常工作时其荷电状态处于最小值SOCmin与最大值SOCmax之间,在蓄电池工作区间内,将其划分为容量较小区间、容量正常区间和容量较大区间,其中SOCa和SOCb分别为容量正常区间内荷电状态的上下限值。荷电状态区间如图2所示。
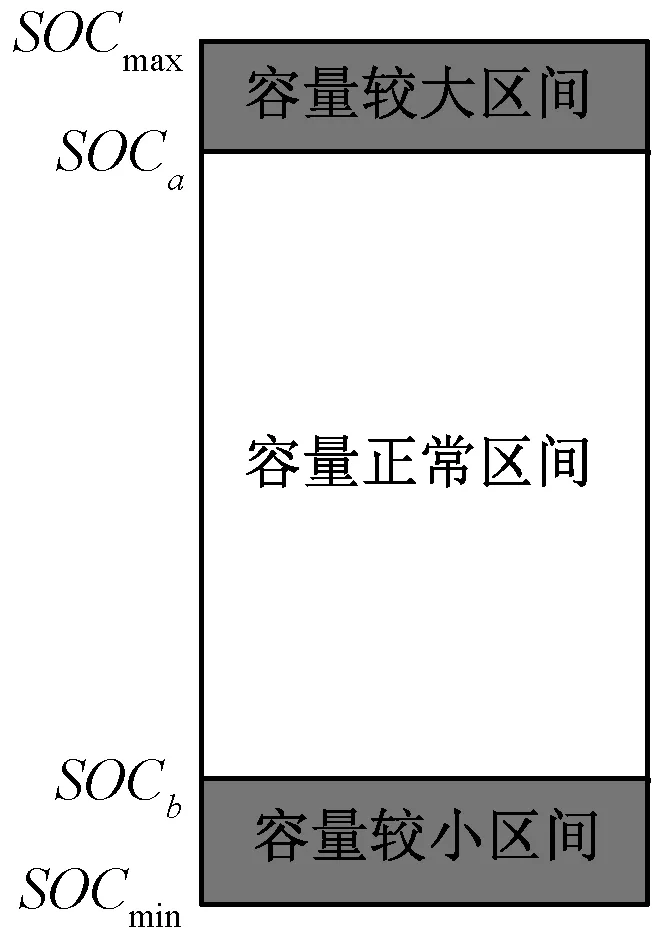
图2 蓄电池荷电状态区间
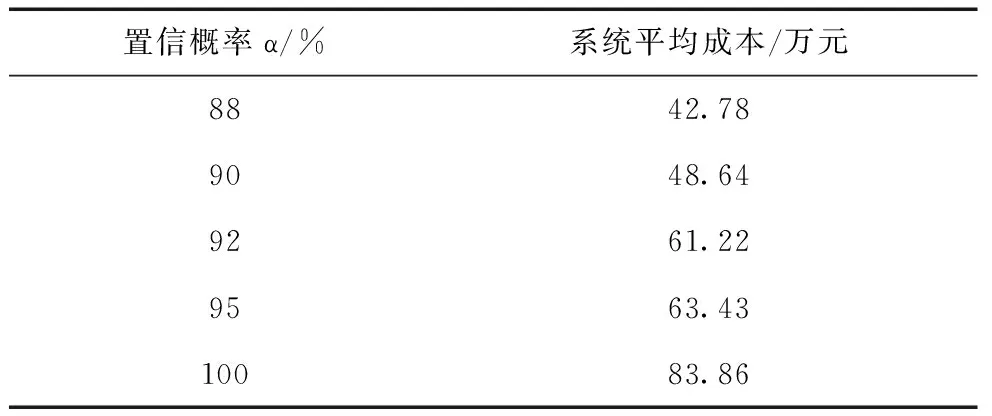
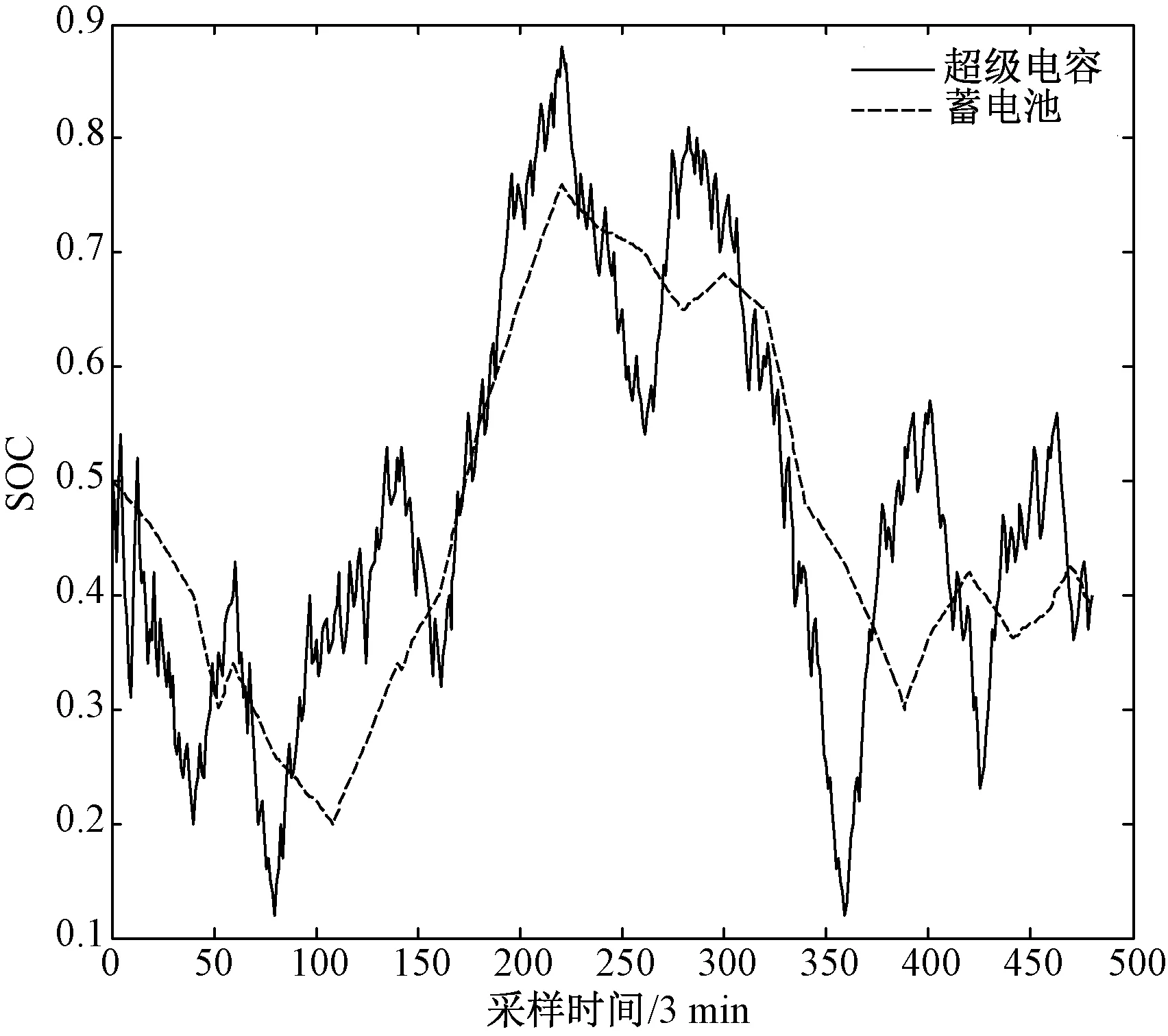
(1)(SOCb Pb_ref=Pb_ref1 (14) (2)(SOCmin (15) (3)(SOCa (16) 混合储能系统平抑风电出力波动中,最佳效果是确保平抑后风电出力与目标功率之间的差额限制在某个允许范围内。而风电出力具有随机性,将不时出现剧烈出力波动,若要保证其出力与目标功率之间差额完全处于该限制范围,需要增加储能装置的容量,相应的投资也将增大。而实际运行中,风电出力的恶劣情形不会如此频繁,如果储能装置的容量过大,结果则是储能装置的运行区间在很小的范围之内,造成容量的浪费,极不经济。因而从经济性与平滑效果两方面进行折中处理,本文采用机会约束规划建立模型,在保证平滑效果的同时,尽可能节省成本。 针对风电出力的平滑效果,以风电功率平滑率来作为衡量混合储能系统补偿风电出力的指标。风电出力平滑率为风电出力加上混合储能系统参考补偿功率与风电目标功率的差值对目标功率的比值[10],其大小在0~1之间,值越小则反应平滑效果越好。 (17) 考虑到混合储能系统经济性,以系统平均成本最小为目标函数建立模型。成本主要由储能装置的初始投资成本、运行维护成本组成。 minC=C1+C2 (18) C1=CEbEb_re+CEscEsc_re+CPbPb_re+CPscPsc_re (19) C2=Lsc(Csc_fM+Csc_vM)+Lb(Cb_fM+Cb_vM) (20) 式中:C1为混合储能的初始投资成本;C2为储能装置的运行维护成本;Pb_re和Psc_re分别为蓄电池和超级电容的额定功率;CEb和CEsc分别为蓄电池和超级电容的单位容量成本;CPb和CPsc分别为蓄电池和超级电容的单位功率成本;Cb_fM、Csc_fM与Cb_vM、Csc_vM分别为蓄电池和超级电容的年固定运维成本和年可变运维成本;Lsc和Lb为超级电容和蓄电池的使用年限。 约束条件主要包含储能装置的功率约束、容量约束,而风电出力平滑效果则以机会约束形式给出。 (21) 选取某典型日内风电出力数据为例进行分析,其中最大出力为270 kW,最小出力为140 kW。低通滤波器的时间常数设置为TL=100 s,高通滤波器时间常数设置为TH=1 s;超级电容荷电状态工作区间为0.1~0.9,蓄电池荷电状态工作区间为0.2~0.8;风电平滑率范围设置为±0.02,采样时间Δt=3 min。储能设备的各项参数指标如表1所示。 表1 超级电容和蓄电池单价 为说明混合储能系统对风电出力波动平抑的效果,选取3个置信概率进行仿真分析,不同置信概率下的风电平抑效果如图3所示。 由图3可知,风电原始出力波动幅度较大,经由混合储能系统补偿后,其出力波动得到较好的平滑。所选的3个置信概率中,置信概率为0.92时风电出力的平滑效果最佳,在面对较大出力的情形,只有极小部分出力波动超出设定范围;置信概率为0.88时平滑效果较差,虽也能适应一般的风电出力波动,但在出力变化剧烈的情形下,将无法满足设定功率的需求;置信概率为0.9时,系统的平滑效果介于二者之间,此时系统已具备抵御一定出力突变的能力,即使出力突变,系统对风电出力的平滑效果也能满足基本的需求。 为研究置信概率α对混合储能系统成本的影响,通过改变置信概率进行不断仿真,得到不同置信概率下对应的平均成本,如表2所示。 从表2中可以看出,随着置信概率的增大,系统所需花费的平均成本也随之上升。置信概率由0.88增大到0.9时,需要增加5.86万元的成本;而置信概率由0.9增大到0.92时,成本却加大了12.58万元。因为风电出力的随机性,存在着一些出力的剧烈波动,随着置信概率的增大,面对这些较大波动时,对平滑率要求也越来越严格,相对应的储能装置的功率和容量必将增加,故而需要投入更多的成本;尤其在置信概率为1时,平均成本到达了83.86万元,极不经济。而根据对图3的分析可知,置信概率为0.88时,系统的整体平滑效果还达不到要求;置信概率为0.9时,已能很好的满足目标功率的需求,虽然继续增加置信概率能更好的保证系统的平滑效果,但其主要是针对少量巨大波动的处理,因而相较置信概率为0.9时变化已然不大,所花费的成本却巨额增加,与所反映出来的效果不成正比。 表2 不同置信概率对应的成本 综合经济性与平滑效果,在对平抑风电波动分析中,选取置信概率为0.9进行仿真计算,得到的超级电容和蓄电池的额定功率和容量如表3所示。 表3 置信概率0.9时的最优配置 按表3配置的混合储能系统工作时,超级电容和蓄电池的荷电状态如图4所示。 图4 超级电容和蓄电池荷电状态 由图4可知,超级电容和蓄电池组成的混合储能系统中,蓄电池的充放电次数较少,这是由于风电出力的波动高频部分由超级电容进行补偿,蓄电池只需补偿其低频部分,故而其充放电次数较少。而且,采取限值处理措施后,工作时其荷电状态长时间位于容量正常区间内,保证蓄电池不会出现过充或过放。对于超级电容,其充放电较频繁,与其特性相符;荷电状态虽然变动幅度较大但极少达到极值,这是由于采取了预先处理,在出力波动剧烈时段,提前将一部分功率转移到蓄电池,故而超级电容荷电状态会向中间位置偏移,出现极值的情形也大大减少。 论文采用混合储能系统平抑风电出力波动得到结论如下: (1) 利用机会约束规划模型描述混合储能系统的平抑效果,在得到最优储能配置的同时,能更好地节省混合储能系统平均成本。 (2) 在超级电容中加入预先处理环节,保证其不致因容量小的特点长期处于限值状态而失去对风电出力波动的平抑效果。 (3) 对蓄电池引入超级电容加限值措施的双重保护,极大地延长其工作周期,从侧面减少了整个系统的投资。 (4) 针对蓄电池和超级电容寿命问题,可加以更具体的量化分析,以期能寻求更好的控制策略。 [1]李春曦,王佳,叶学民,等. 我国新能源发展现状及前景[J]. 电力科学与工程,2012,28 (4):1-8. [2]张立梅,唐巍,赵云军,等. 分布式发电对配电网影响的综合评估[J]. 电力系统保护与控制,2010,38(21):132-135. [3]王培波,张建成. 超级电容器储能系统并网控制研究[J]. 电力科学与工程,2009,25 (6):1-4. [4]汪海蛟,江全元. 应用于平抑风电功率波动的储能系统控制与配置综述[J]. 电力系统自动化,2014,38 (19): 126-135. [5]LIU F C,LIU J J,ZHOU L Y. A novel control strategy for hybrid energy storage system to relieve battery stress[C]//Hefei:IEEE,2010. [6]QU L,QIAO W. Constant power control of DFIG wind turbines with supercapacitor energy storage[J]. IEEE Trans on Industry Application,2011,47 (1):359-367. [7]张晴,李欣然,杨明,等. 净效益最大的平抑风电功率波动的混合储能容量配置方法[J]. 电工技术学报,2016,31 (14):40-48. [8]盛四清,刘梦. 一种同时考虑DG和ESS选址定容的主动配电网规划方法[J]. 电力科学与工程,2015,31 (10):21-26. [9]王博堃,滕欢,胡晓通,等. 基于平滑控制策略的混合储能优化配置方法[J]. 高压电器,2015,51 (10):47-53. [10]谢石骁,杨莉,李丽娜. 基于机会约束规划的混合储能优化配置方法[J]. 电网技术,2012,36 (5):79-84. [11]李军徽,高天宇,赵冰,等. 抑制风电功率波动的电池储能系统自适应控制策略设计[J]. 储能科学与技术,2015,4 (3):278-283. [12]佘慎思,李征,蔡旭. 风储联合发电系统电池荷电状态和功率偏差控制策略[J]. 电力系统自动化,2014,38 (20):9-17. [13]罗鹏,杨天蒙,娄素华,等. 基于频谱分析的微网混合储能容量优化配置[J]. 电网技术,2016,40 (2):376-381. [14]程杉. 含分布式电源的配电网多目标优化问题研究[D]. 重庆:重庆大学,2013. [15]丁明,林根德,陈自年,等. 一种适用于混合储能系统的控制策略[J]. 中国电机工程学报,2012,32 (7):1-6.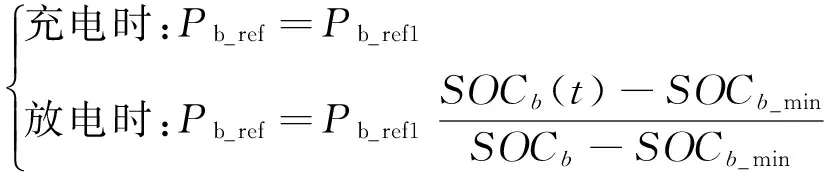

3 混合储能优化配置模型
4 算例仿真


5 结论
