电动车车架数值分析下的网格特性分析与研究
2018-03-21王宝中郭灿志刘佳鑫于玉真
王宝中 ,郭灿志 ,2,刘佳鑫 ,3,于玉真
(1.华北理工大学 机械工程学院,河北 唐山 063009;2.北京理工大学 机械与车辆学院 北京 100081;3.华中科技大学 能源与动力学院,湖北 武汉 430074)
1 引言
车架是电动汽车的脊梁,直接或间接支撑连接汽车的各总成零部件,也是汽车的装配基体和承载基体,承受来自车内外的各种载荷,其好坏直接关系到整车的性能和质量[1]。在设计过程中对车架进行有限元分析成了必不可少的一步,确保分析结果的准确性是仿真分析的必然要求。
在文献[2]中,我们可以知道在有限元分析计算中,网格数量越多,数值模型的网格质量越好、失真度越低,得到的仿真分析结果越准确。在理论上讲,就是因为当前偏微分方程主流的数值离散方法都是先计算单元节点上的位移、应力等物理量,然后通过插值的方式求取节点间的值,所以才会出现网格单元疏密对结果的影响。尽管其在做网格质量分析研究中的单元质量可能并不是最优的,但是也可以作为网格划分质量的好坏直接影响了分析结果可靠度的一种证明方式。文献[3]利用有限元法对全地形车防滚架在大石块工况、泥坑、陡坡等所有非路面工况中仍然保证人员安全的条件下,对其进行了优化和轻量化,在车架设计和分析中使用有限元法已经成为必然;文献[4]用Hypermesh和ANSYS联合仿真的方法得到了全地形车车架的模态参数,包括模态振型和振动频率,从而避免了发动机和车架共振并且使各种工况下车架的应力最优化。拟对某电动车车架有限元分析过程中的网格对结果的影响程度特别是网格无关解问题进行分析和研究。所研究纯电动旅游观光车,由于体积较小、方便灵活、视野宽阔非常适合用于景区或厂区,如图1所示。

图1 纯电动旅游观光车Fig.1 Pure Electric Sightseeing Vehicles
2 仿真模型及误差
2.1 物理模型
为提高计算效率在进行模型绘制时对不影响车架强度和主要力学特性的部位进行了简化处理(如略去功能件、装饰件和部分倒圆角等),在CREO中对原车架进行三维建模,然后利用Workbench软件成熟的双向CAD接口,把三维车架数字模型导入Workbench中。其中Ⅰ-Ⅷ处均为主要载荷承受位置。在满载情况时,其载荷大小分别为500N、1000N、1600N、1000N、2400N、500N、2400N、900N;车架自重采取对其施加重力加速度的方式进行计算。该车身骨架各构件型材主要采用8#和6.3#槽钢、32×2.5方钢和部分40×40×3角钢,整个车身骨架全部由普通碳素结构钢Q235焊接成型,在工作时可认为其变形是弹性变形且各向材料同性[5];材料弹性模量E=2.07105MPa、泊松比=0.3、密度 ρ=7850kg/m3、屈服极限为 235MPa。
2.2 有限元模型
有限元分析法的基本思想就是将物体(连续求解域)离散划分成有限多个按一定方式相互联结在一起的小单元体,并在每个单元上指定有限多个节点,求解过程中首先求出的是节点的物理量(如位移量),然后利用插值函数确定单元内任意一点的物理量值。当网格大小精确到原子量级时,比如对于铁来说,当56克的铁单质被划分成为1mol个单元体时(大约为6.02×1023个),完完全全就是实际中的情况了,称有限元为“数值模拟仿真”就显得有些不恰当了。但是,对于现在的计算机硬件来说是不现实的,不可能完成那么大的计算量,即使能完成计算任务而花费了相当长的时间也是非常不值得的。再者,计算机浮点计算时的舍入误差也会随着网格密度的增大、数量的增多而增大,所以对于实际情况来说盲目的缩小网格尺寸、增加网格数量是不可取的。网格划分的一般流程,如图2所示。
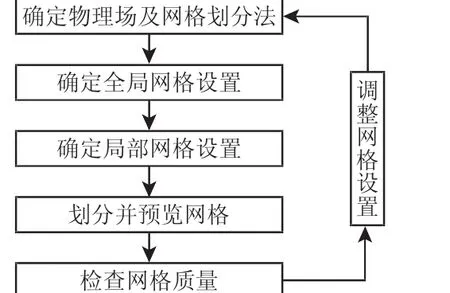
图2 网格划分的流程Fig.2 Meshing Process
由于该车架结构相对复杂,在分析过程中采用实体SOLID187单元用Workbench先后对车架进行了两次网格划分,单元数分别为24620、412155,节点数分别为56771、807232。为了能够清楚的表达有限元模型的外观,获得更好的视觉效果,在此返回到MechanicalAPDL经典界面,进而把有限元模型设置为可以传递更多信息的模型状态,如图3、图4所示。此次车架前后两次划分的有限元模型的另外一种表达方式,其中一种颜色的小块代表一个单元。尤其从图3中可以清楚的看到网格中各个颜色的单元,网格尺寸很大,数量比较少。图4则网格数量比较多,尺寸比较小,在这么小的图幅上几乎都要分不清楚了。

图3 单元数为24620的有限元模型Fig.3 Finite Element Model of Unit Number is 24620

图4 单元数为412155的有限元模型Fig.4 Finite Element Model of Unit Number is 412155
2.3 分析结果对比
本节结合非公路用旅游观光车的特点,即观光车为景区内用车,通常情况下为满载运行并且车速也不太高,而景区路面条件较好,所以车架受力主要按照非公路用旅游观光车最常见的工况之一的满载弯曲工况为例进行车架静态特性分析[8-9],此工况为电动车在水平面上静止或匀速行驶时,不受其他外力的状态。当完成这些基础工作后就可以进行求解计算了,这里直接调用的是workbench中的Mechanical求解器,但是本质上它其实也是经典ANSYS中的MechanicalAPDL求解器。其分析结果对比,如表1所示。在这个例子中,两者的相对误差都达到了59.5%,甚至75%以上,前后两次的位移变形云图(图略)。两次的形变大小不同,但位置大致相同,都在车架中部,表现为向下弯曲变形。

表1 分析结果数据对比表Tab.1 Comparison of the Results of Analysis Data
2.4 误差产生的原因分析
在上小节的计算中,在边界条件和硬件系统相同、仅仅在网格数量不等的情况下,计算结果却出现这么大的偏差。说明对于一个特定的模型,网格数量和质量影响到了计算结果的准确性。有必要对网格特性作进一步的研究,用优化设计的方法解决这个问题。从2.2中介绍的有限元分析法原理中了解到,网格数量的增加肯定会提高计算的精度,同时也必然会增加求解的时间和费用。为平衡这个矛盾,找到一个网格密度值,使任意一个几何模型当网格密度处在这个值附近时,相邻两次的计算结果相差不多,必然就会引入了一个概念:网格无关性[10]。
3 网格无关性分析
3.1 网格特性
网格无关性换言之就是对于任意一个数值模型,其网格数量存在一个临界点,网格数量超过这个点后对计算结果影响很小,其误差可以被忽略。而在这个临界点时,既可以保证计算结果精度的可靠性,也可以确保计算规模在计算机能够承受的范围之内,这个点我们就称其为网格无关性的阈值。为了验证三排正向座车架底盘数值模型的网格无关性,在模型结构参数、载荷属性和边界条件相同的前提下,本节共做了八组分析,网格数量分别为:24620、33394、66553、85712、142701、233145、272828 和 412155,节点数分别为:46771、66240、136210、175957、294472、477798、551452、807232。为方便对比结果,采用车架的位移变形值和最大等效应力作为评价参数,相邻两次分析计算结果的比值作为评价标准。其分析结果数据对比,如表2所示。
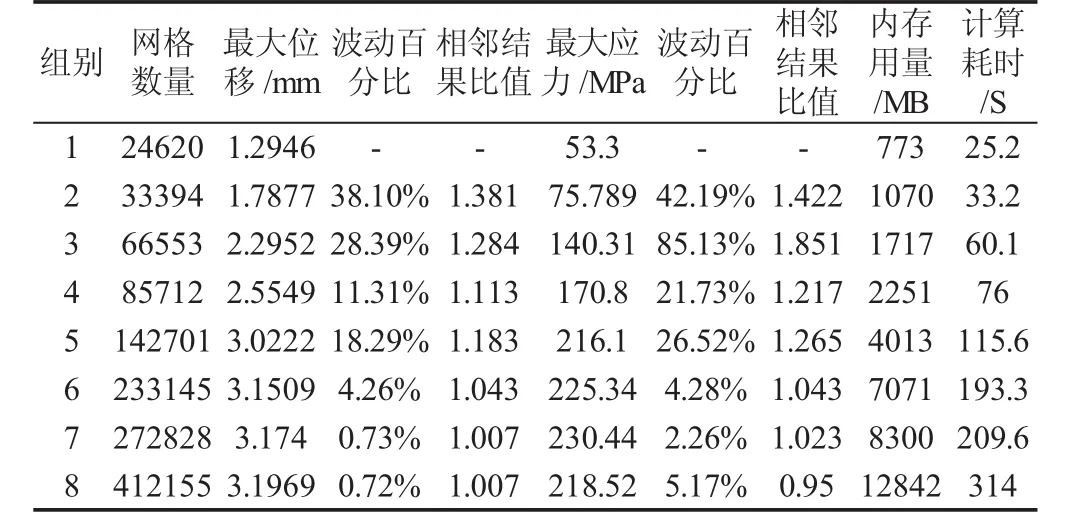
表2 分析结果对比表Tab.2 Comparison of Results
由表2可以看出,波动比越来越小,内存用量和计算耗时随着网格数量的增加而增大。网格数量与最大位移变形、最大等效应力之间的关系分别,如图5、图6所示。

图5 网格数量与变形之间的关系Fig.5 Relationship Between Grid Numbers and Deformation
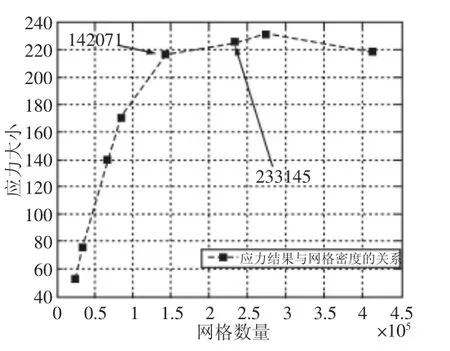
图6 网格数量与应力之间的关系Fig.6 Relationship Between Grid Numbers and Stress
由图5可知,位移变形值随网格数量的增加而逐渐增大。在网格数量小于142071时,位移变形值随网格数量增加而增加的趋势非常明显,而当网格数量大于142071后,其上升趋势逐渐减缓;当网格数量超过142071后,其位移变形值的波动已经小于5%。另由图6也可以看到,前五组分析值在曲线图中近乎直线上升,当网格数量超过142071后,最大应力值变化趋势才趋于平缓,后几组值的波动率也小于5%(第八组数据应力波动率也是在5%附近)。确定142071为其阈值,分析计算的两个极值点相对阈值点的计算耗时差分别为组1减少了90.4s,组8则增多了将近200s。

图7 前四组位移变形云图Fig.7 Frist Four Nephograms of Displacement Deformation
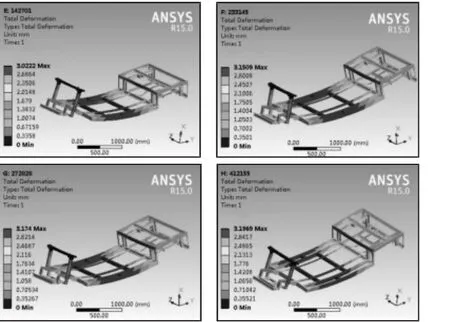
图8 后四组位移变形云图Fig.8 Last Four Nephograms of Displacement Deformation

图9 前四组最大等效应力云图Fig.9 Frist Four Nephograms of Equivalent Stress
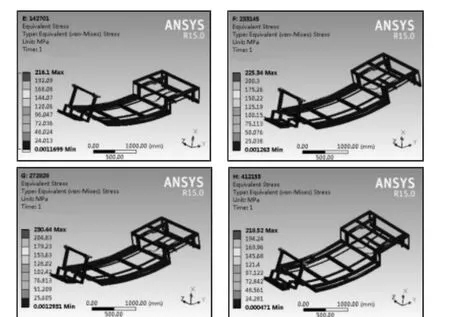
图10 后四组最大等效应力云图Fig.10 Last Four Nephograms of Equivalent Stress
分析过程中的八组位移变形云图及最大等效应力云图分别见图7(前四组位移变形云图)、图8(后四组位移变形云图)、图9(前四组最大等效应力云图)、图10(后四组最大等效应力云图)。图7~10中,每张大图中有四幅小图,从左到右、从上到下分别对应的是第 1、2、3、4 和 5、6、7、8 组的计算数值,其中所有小图的项目编号就是进行该组分析时的网格数量值。
在几组分析结果中看到,变形和应力的大小都不同,变形从第一组的1.2946mm一直增大到第八组的3.1969mm,应力从第一组的53.3MPa一直增大到第七组的230.44MPa,第八组应力值有所减小,可能是由于计算机计算时的舍入误差所致。但是最大变形位置和最大应力位置基本上相同,最大变形位置在车架中部,主要表现为向下弯曲;最大应力位置在车架后悬架支点处。
3.2 试验验证
为验证仿真结果的准确性,在电动车满载情况下,采用STRAINBOOK616高速动态数据采集仪对车架后悬架支点处的应变进行采集,然后根据应变应力的正比关系转换成应力。后悬架支点处每侧布置三个采集点,采集数据取最大值,两侧应变最大值分别为:εmax1=0.001054;εmax2=0.001060。根据公式 σ=Eε,得到两侧应力最大值分别为:σmax1=217.124MPa;σmax2=218.36 MPa。
可以看到实验结果与在网格无关解的仿真结果基本吻合,而比网格质量较差的第四组结果有较大的误差。而与第七组结果不同的主要原因在于如果车架的三维模型有型材垂直相交的时候,workbench就认为它是垂直相交的,如图11左所示。但实际中即使存在垂直相交的情况,也会有一定的圆角存在,尤其是当相交处是一焊缝时,如图11右所示。
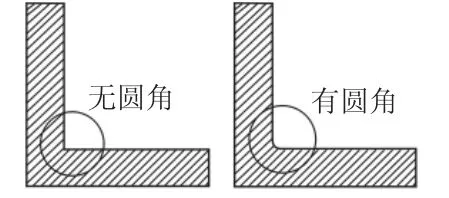
图11 模型对比Fig.11 Comparison of Models
3.3 数学模型建立
针对车架底盘这个特定的模型,在定网格类型下,在MATLAB环境下用多项式拟合法得到了网格数量x与变形D和应力S之间的关系式如下:
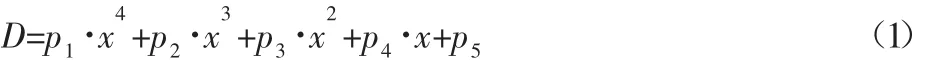
其中,p1=-5.079×10-22;p2=5.486×10-16;p3=-2.714×10-10;p4=3.829×10-5;p5=0.5831。
拟合方程D的均方根误差为0.1089。
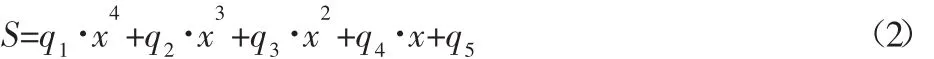
其中,p1=-4.164×10-20;p2=4.676×10-14;p3=-1.961×10-8;p4=3.65×10-3;p5=-26.05。
拟合方程S的均方根误差为2.8714。式(1)、式(2)就是底盘模型在定网格类型下的数学模型,在计算求解时可以根据此模型在确定误差范围后找到网格无关解的阈值范围,进而求出最终准确解。
一般工程中,当误差率小于5%时,可以认为是允许误差。在此次的分析案例中,结果可以认为当网格数量超过142071后,其变化对位移变形和最大等效应力的计算影响可以被忽略不计,即网格数量与车架的动静态特性没有关系,这样就消除了离散几何模型对数值计算结果产生的误差,得到相对准确的仿真分析结果。
4 结论
结合国内某微型电动车,在ANSYS软件环境中对物理模型进行数值计算,结合计算结果,寻找致使分析结果偏差过大的原因,并通过对网格特性系统的研究。最终得到结论如下:(1)在一定条件下,2万较41万网格模型最大应力差异约为75.52%,最大位移差异约为59.5%,网格特性特别是网格数量对结果影响较为明显,确定网格会影响分析结果,证明有限元计算具有网格相关性。(2)该车架模型在网格数量大于142071后,差异减少,确定142071为其无关解阈值;应用拟合的最大应力和最大位移关于网格数量的函数表达式,可迅速查询或计算仿真结果的误差范围;对任意一个特定的模型进行分析时必须对其进行网格无关性的讨论,以得到允许误差范围内的计算结果。(3)该方法有利于应用在工作量较大、对象单一、重复性强的仿真分析之中,有利于提升设计效率,拓展设计手段。
[1]Beermann.H.J.Statie ana1ysis of eommereia1 vehie1e frames:ahybrid finite elementanaly tieal.International Journal of Vehiele Design,1984(5):26-52.
[2]路春光,郭灿志,刘宝刚.微型电动车车架静态及预应力模态分析研究[J].制造业自动化,2015(12):11-14.(Lu Chun-guang,Guo Can-zhi,Liu Bao-gang.Research on static and prestressed modal analysis of micro electric vehicle frame[J].Manufacturing Automation,2015(12):11-14.)
[3]P.Anjani Devi,A.Dilip.Design and optimisation of sae mini baja chassis[J].International Journal of Engineering Research and Applications,2014(4),9:93-97.
[4]Jing Wang,Yong Wang.Study on structure dynamic characteristic of all terrain vehicle frame[J].Advanced Materials Resesrch,2013(798-799):255-258.
[5]杨卓.低速纯电动汽车车架的轻量化研究[D].广州:华南理工大学,2014.(Yang Zhuo.Research on lightweight frame speed of pure electric vehicle[D].Guangzhou:South China University of Technology,2014.)
[6]鲁建霞,苟惠芳.有限元法的基本思想与发展过程[J].机械管理开发,2009(2):74-75.(Lu Jian-xia,Gou Hui-fang.Basic idea and development process of finite element method[J].Mechanical Management and Development,2009(2):74-75.)
[7]朱剑平.8×4轻量化公路自卸车车架的开发与设计[D].西安:西安石油大学,2011.(Zhu Jian-ping.The weight reduction design of 8×4 dump truck frame[D].Xi’an:Xi’an Shiyou University,2011.)
[8]沈永峰,郑松林,冯金芝.公路客车车架与车身骨架强度及模态分析[J].现代制造工程,2013(7).(Shen Yong-feng,Zheng Song-lin,Feng Jin-zhi.Strength and modal analysis for highway bus frame and bus body frame[J].Modern Manufacturing Engineering,2013(7).)
[9]吕东升,王东方,苏小平.基于Hyperworks的某客车车架有限元分析[J].机械设计与制造,2011(3).(Lv Dong-sheng,Wang Dong-fang,Su Xiao-ping.A static research of bus frame based on HYPERWORKS[J].Design&Manufacture,2011(3).)
[10]徐振元.工程车辆波纹翅片散热器特性分析与应用研究[D].长春:吉林大学,2012.(Xu Zhen-yuan.Research on characteristics and application of wave fin radiator in engineering vehicle[D].Changchun:Jilin University,2009.
