平行不对中转子系统的电机电流特性

郭伟杰 ，杨兆建 ，石江波 ，李 峰

（1.太原理工大学 机械工程学院，山西 太原 030024；2.煤矿综采装备山西省重点实验室，山西 太原 030024）

1 引言

转子系统是旋转机械的核心部件，而不对中是最为常见的故障之一，约占总故障的60%[1]，因而国内外学者关于转子系统不平行故障的研究有很多。文献[2]建立了不平行转子系统的动力学模型，研究了转子系统在平行不对中故障下的非线性行为；文献[3]研究了刚性联轴器在平行不对中故障下轴心轨迹随转速、质量偏心、不对中量等因子的变化规律；文献[4]从转速、质量偏心、不对中量和阻尼系数等几方面研究了平行不对中故障下转子系统的弯扭耦合特性；文献[5]主要研究了齿式联轴器不对中故障下转子系统的弯扭耦合振动；文献[6]推导出了在非线性油膜作用力下平行不对中转子系统的动力学模型，并用数值方法重点分析了了系统的非线性行为；文献[7]建立了双转子不对中故障系统动力学模型，揭示了高低压转子的振动特性；文献[8]建立了齿式联轴器不对中转子轴承系统的有限元模型，得出了不对中量和稳态响应之间的量化关系；文献[9]通过分析刚性联轴器的不对中问题，建立了刚度随时间变化的线性系统模型；文献[10]基于有限元分析建立了考虑花键联轴器不对中效应的转子系统动力学方程，数值计算模拟出不对中啮合力对转子-花键联轴器系统动力学特性的影响规律；文献[11]分析了在膜片式弹性联轴器不对中情况下，滑动轴承支撑的多盘转子系统的非线性动力特性和稳定性；文献[12]建立了考虑电机联轴器影响的双盘不对中-碰摩耦合故障转子系统力学模型和有限元模型，研究了碰摩刚度和不对中角度两个重要参数对系统动力学特性的影响。综上所述，大部分的文献都是通过振动分析方法来研究转子系统的不对中故障，而将电流分析方法应用到转子系统的平行不对中故障的研究相对较少。

针对转子系统联轴器平行不对中故障，以不对中故障与质量偏心产生的惯性扭矩和电机的电磁扭矩为纽带，在MATLAB/Simulink中建立转子系统机电耦合仿真模型，对电机电流信号进行频域分析，研究转子系统在平行不对中故障下与电机电流信号的耦合特性。

2 平行不对中转子系统动力学模型

四支两跨不平行转子系统示意图，如图1所示。假设转子系统简化为质量分别为和的圆盘与弯扭柔性的无质量轴，并且转轴各向同性，轴承为刚性支撑。不对中转子系统坐标示意图，如图2所示。

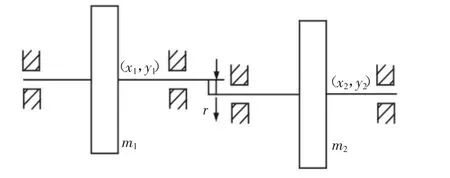
图1 转子系统示意图Fig.1 Sketch of Rotor Systems

图2 不对中转子系统坐标示意图Fig.2 Coordinate Systems of Misaligned Rotor Systems

图中：O—涡动中心；O1和O2—单元盘1和单元盘2的形心，坐标分别为 （x1，y1），（x2，y2）；r—转子 1 和转子 2 的平行不对中量，为恒定值；θ—转子2绕转子1的形心转过的角度，假设转子系统稳定运行，则：θ=ωt+δ2+β

式中：ω—转子系统的旋转速度；δ2—转子2的扭振角位移；β—初始相位角。则：x2=x1+rcosθ，y2=y1+rsinθ。

由理论力学可知，刚体的平面运动分解为刚体质心的平动和刚体绕质心的转动，所以四支两跨转子系统的动能可以表示为：T=TG+TR。假设转子1存在质量偏心，偏心距为e，φ为圆盘1质心转过的角度，则：φ=ωt+δ1+α

式中：δ1—转子1的扭振角位移；α—初始相位角。则TG和TR可以分别表示为：

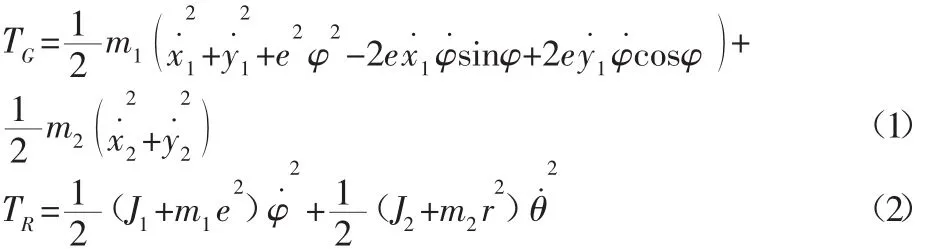
式中：J1、J2—转子1和转子2的转动惯量。

假设两转子的抗弯刚度分别为k和k1，抗扭刚度分别为k2和k3，考虑转轴的线弹性，重力，以及几何对称性，转子系统的势能可以表示为

为了方便化简和计算，假设转子1在x、y方向上存在平动阻尼，阻尼系数为c，在z方向上存在转动阻尼，阻尼系数为c1，忽略转子2的平动阻尼，转子2的转动阻尼系数也为c1，不考虑外激振力和外扭矩，则四支两跨转子系统的广义力为Qx=-cx˙1，Qx=-cy˙1，Qφ=-cφ˙1，Qθ=-cθ˙1将 x1、y1作为系统的广义坐标，令 x1=x，y1=y，整理上式并代入拉格朗日方程可得转子系统的运动微分方程为：

式中：ξ0—转子1的弯振阻尼系数比；ω0—转子1的弯振固有频率；ξ1、ξ2—转子 1 和转子 2 的扭振阻尼系数比；ω1、ω2—转子1和转子2的扭振固有频率。

3 电机模型

首先建立三相异步电机在αβO系统下的仿真模型，在αβO系统下电机的电压方程为：

式中：ω—转子转动角速度；Rs—定子绕组电阻；Rr—转子绕组电阻；Ls—定子绕组自感；Lr—转子绕组自感；Lm—定转子绕组互感；np—电极对数；Te—电磁转矩；Mz—惯性扭矩与外扭矩之和；J0—电机的转动惯量。

4 机电耦合模型仿真分析

4.1 机电耦合模型仿真参数

ω0=75.36rad/s，ω1=ω2=50.24rad/s，m1=m2=10kg，ξ0=0.05，ξ1=ξ2=0.02，J1=J2=0.05kg·m2，ω=1500r/min=157rad/s，k=k1=56791.3N/m，k2=k3=126.2N/m，np=2，f=50Hz，Rs=4.26Ω，Rr=4.26Ω，Ls=0.666H，Lr=0.670H，Lm=0.65H，U=380V，J0=0.05kg·m2。

4.2 平行不对中对转子系统电机电流的影响

当偏心距e=0，不对中量r=0.001m和r=0.002m时，电机电流的频域图，如图3所示。由图3（a）可知，电流信号除了50Hz的工频外，在 17Hz、25Hz、33Hz、67Hz、75Hz以及 83Hz处出现突变，其中，25Hz与 75Hz正好与相对应，fω=25Hz是转子系统

的转频；17Hz、33Hz、67Hz 和 83Hz正好与相对应，fω=18Hz是转子系统的固有扭转频率。保持e=0不变，增大不对中量，由图3（b）可知，42Hz和58Hz的边频分量的幅值有了明显的升高，而这两处频率正好与相对应，即转子系统的固有扭转频率体现在电流信号的边频中。由分析可知：转子系统的平行不对中故障会使电流信号激发出边频分量，但是当不对中量较小时，的边频分量不明显。

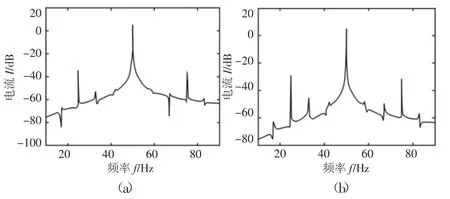
图3 e=0时电机电流频域图Fig.3 Motor Current Spectrum in State of e=0

4.3 质量偏心对转子系统电机电流的影响

当平行不对中量r=0，质量偏心取0.001m和0.002m时，电机电流的频域图，如图4所示。质量偏心与平行不对中故障对电流信号的频谱影响基本相似，只是在34Hz和66Hz处，幅值也产生了突变，这两处的频率正好与相对应，即当转子系统存在质量偏心故障时，会使电流信号激发出的边频，随着偏心距的增大，边频幅值会相应的增大。

图4 r=0时电机电流频域图Fig.4 Motor Current Spectrum in State of r=0

4.4 综合两种故障对转子系统电机电流的影响

综合考虑两种故障，取e=0.002m、r=0.001m和e=0.001m、r=0.002m两种情况，则电流的频谱，如图5所示。当e＞r的情况下，的边频分量比较明显，反之，该边频分量几乎被淹没。

图5 两种故障同时存在时电流频谱图Fig.5 Motor Current Spectrum in State of Two Kinds of Faults

4.5 故障类型对电流边频峰值的影响

将e=0、r=0.002m，e=0.002m、r=0m，e=0.001m、r=0.002m和e=0.002m、r=0.001m四种故障类型下的边频峰值统计，如表1所示。对照故障1和2可知，故障1和故障2在42Hz和58Hz处的波峰值相差不大，而在其它边频处，故障1的峰值明显比故障2的峰值高，即平行不对中故障相比于质量偏心对电流的的边频峰值影响较大，而的边频峰值对两种故障并不敏感。分别对照故障1、3和故障2、4可知，故障3和4的边频峰值明显比故障1和2的峰值大，即转子系统在两种故障的综合作用下出现了峰值的叠加，而且对比故障1、3和故障2、4这两组故障类型的边频峰值的增大程度，可以发现后者峰值的增大程度明显比前者大，即相比较于质量偏心，平行不对中故障对电流信号的边频峰值更为敏感。

表1 不同故障类型下的电流边频峰值（dB）Tab.1 The Table of Current Edge Frequency Peaks under Different Fault Types（dB）

5 结论

考虑转子系统的平行不对中与质量偏心故障，以故障产生的惯性力矩和电机的电磁扭矩为纽带，建立电机与转子系统的机电耦合仿真模型，并用傅里叶变换对电机电流信号进行频谱分析，主要结论如下：（1）若转子系统只存在平行不对中故障，则会使电流信号激发出的边频分量，而且随着不对中量的增大，还会激发出的边频分量。（2）若只考虑转子的质量偏心故障，则电机电流信号会产生的边频分量，而且随着偏心距的增加边频分量越明显，峰值也会变大。（3）当两种故障都存在时，若r＞e时，的边频分量会被淹没，反之则幅值比较明显。（4）相比较于质量偏心故障，电流信号的的边频峰值对转子系统的平行不对中故障更为敏感，而的边频峰值对两种故障并不敏感。（5）转子系统在两种故障的综合作用下，边频峰值明显比单一故障下的边频峰值要大，即出现故障的叠加作用，而且从两者增大的程度来看，相比较于质量偏心，平行不对中故障对电流信号的边频峰值更为敏感。

［1］赵营豪，陈宏，朱朝鹏.转子不对中定量研究［J］.机械设计与制造，2013（12）：109-110.（Zhao Ying-hao，Chen Hong，Zhu Chao-peng.Research on the quantitative of misalignment［J］.Machinery Design&Manufacture，2013（12）：109-110.）

［2］李明.平行不对中转子系统的非线性动力学行为［J］.机械强度，2005，27（5）：580-585.（Li Ming.Nonlinear dynamic behavior of parallel misaligned rotor system［J］.Journal of Mechanical Strength，2005，27（5）：580-585．）

［3］安学利，周建中，向秀桥.刚性联接平行不对中转子系统振动特性［J］.中国电机工程学报，2008，28（11）：77-81.（An Xue-li，Zhou Jian-zhong，Xiang Xiu-qiao.Vibration characteristics of two rotors connected by rigid coupling with parallel misalignment［J］.Proceedings of the CSEE，2007，28（11）：77-81.）

［4］付波，周建中，彭兵.固定式刚性联轴器不对中弯扭耦合振动特性［J］.华中科技大学学报：自然科学2007（4）：96-99.（Fu Bo，Zhou Jian-zhong，Peng Bing.Coupled lateral and torsional vibration properties of parallel misaligned fixed rigid couplings［J］.Journal of Hua Zhong University of Science and Technology，2007，35（4）：96-99.）

［5］何成兵，顾煜炯，杨昆.齿式联接不对中转子的弯扭耦合振动特性分析［J］.机械强度，2005，27（6）：725-729.（He Cheng-bing，Gu Yu-jiong，Yang Kun.Properties analysis on coupled lateral and torsional vibrations of the rotor connected by the gear coupling［J］.Journal of Mechanical Strength，2005，27（6）：725-729.）

［6］李自刚，李明，江俊.不对中联轴器-柔性转子系统非线性动力学行为［J］.动力学与控制学报，2014（1）：30-35.（Li Zi-gang，Li Ming，Wang Jun.Nonlinear dynamics of a flexible rotor system coupled by a misaligned coupling［J］.Journal of Dynamics and Control，2014（1）：30-35.）

［7］李全坤，廖明夫，蒋云帆.双转子不对中故障振动特性分析［J］.机械科学与技术，2014，33（12）：1916-1920.（Li Quan-kun，Liao Ming-fu，Jiang Yun-fan.The vibration features analysis of twin spool rotor with misalignment fault［J］.Mechanical Science and Technology for Aerospace Engineering，2014，33（12）：1916-1920.）

［8］雷文平，韩捷，李志胜.齿式联轴节不对中转子的动力学响应分析［J］.机械强度，2012，34（3）：327-332.（Lei Wen-ping，Han Jie，Li Zhi-sheng.Dynamic response analysis of the rotors connected by the misaligned gear coupling［J］.Journal of Mechanical Strength，2012，34（3）：327-332.）

［9］Lees A W.Misalignment in rigidly coupled rotors［J］.Journal of Sound&Vibration，2007，305（s1-2）：261-271.

［10］赵广，刘占生，叶建槐.转子-不对中花键联轴器系统动力学特性研究［J］.振动与冲击，2009，28（3）：78-82.（Zhao Guang，Liu Zhan-sheng，Ye Jian-huai.Meshing force model of misaligned gear coupling and its influence on a rotor system［J］.Journal of Vibration and Shock，2009，30（1）：33-39.）

［11］万召，荆建平，孟光.弹性联轴器不对中转子-轴承系统的非线性动力特性及稳定性研究［J］.振动与冲击，2012，31（24）：20-25.（Wan Zhao，Jing jian-ping.Nonlinear dynamics behaviors and stability of a rotor-bearing system with flexible coupling misalignment［J］.Journal of Vibration and Shock，2012，31（24）：20-25.）

［12］刘杨，太兴宇，姚红良.双盘转子轴承系统不对中-碰摩耦合故障分析［J］.振动、测试与诊断，2013，33（5）：819-823.（Liu Yang，Tai Xing-yu，Yao Hong-liang.Study on misalignment-rubbing coupling fault of dual-disk rotor-bearing system including the impact of motor couping［J］.Journal of Vibration，Measurement&Diagnosis，2013，3（5）：819-823.）